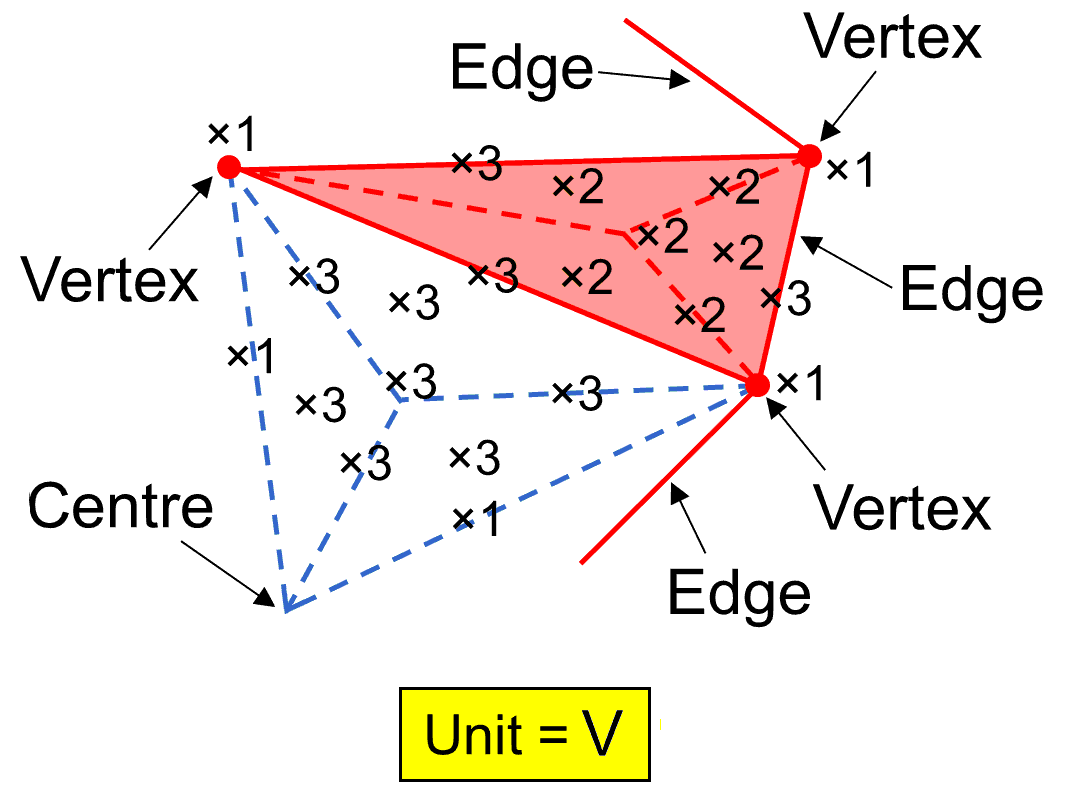
Number weights for a polyhedron with (2+V) vertices, 3V edges & 2 V triangular faces.
| << Previous 1... 14 15 16 [17] 18 Next >> |
The axis of the disdyakis triacontahedron is surrounded by 60 vertices, 180 edges and 120 triangular faces; the axis of the 144 Polyhedron, the second member of the Polyhedral Tree of Life, is surrounded by 72 vertices, 216 edges and 144 triangular faces. Notice that in each polyhedron the proportion vertices:edges:faces is 1:3:2. This means that the ratio of the numbers of such vertices of the 144 polyhedron and disdyakis triacontahedron, namely, 72/60 = 6/5, is the same for the numbers of edges: 216/180 = 6/5, and for the numbers of faces: 144/120 = 6/5. All combinations of corresponding corners, sides and triangles must be in the same ratio. This is a very useful property when the geometrical properties of the two polyhedra are compared or added together. For example, we saw in #12 & #13 that 1680 geometrical elements surround the axis of the disdyakis triacontahedron. We can immediately infer that the number of geometrical elements surrounding the axis of the 144 Polyhedron is 6/5×1680 = 2016. As the number of edges and the number of faces in each case are, respectively, three times and two times the number of vertices that surround the axis (let us call it "V"), every calculation of the number of geometrical elements of a given type for either polyhedron reduces to multiplying V by the number
 |
|
Number weights for a polyhedron with (2+V) vertices, 3V edges & 2 V triangular faces. |
of times that type occurs in a face or an internal triangle with an edge as one of its sides and the centre of the polyhedron as one of its corners. Instead of making tedious calculations involving large numbers, multiplying each time by V, the task of working out the geometrical composition of each polyhedron in terms of points, lines & triangles can be simplefied by making use of the "number weight" associated with that type of element. This is an integer m which, multiplied by the number V, gives the total number of this type that surround the axis of the polyhedron. They are shown above for any polyhedron with (2+V) vertices, 3V edges and 2V Type A triangular faces. It is more instructive, however, to consider the general case where all faces and internal triangles are nth-order triangles and then see what the properties of the two polyhedra are for the first few values of n. Simple triangles are 0th-order, triangles which are divided into their three sectors are 1st-order (also called "Type A triangles" elsewhere in this website), triangles with each sector divided into three sectors are 2nd-order (also called "Type B triangles"), etc. Section 2 of Article 65 calculates the numbers of corners, sides & triangles inside an nth-order triangle to be as follows:
Number of corners = ½(3n − 1);
Number of sides = (3/2)(3n − 1);
Number of triangles = 3n;
Total number of corners, sides & triangles = 3n+1 − 2.
The calculated geometrical weights for a polyhedron of the type defined above are shown below:
Number weights for nth-order triangular faces and internal triangles
| Corners | Sides | Triangles | Total | |
| Faces | 3n | 3n+1 | 2×3n | 2×3n+1 |
| Interior | ½(3n+1 − 3) | ½(3n+2 − 7) | 3n+1 | 3n+2 − 5 |
| Total | ½(5×3n − 3) | ½(5×3n+1 − 7) | 5×3n | 5×(3n+1 − 1) |
Their values for n = 0, 1, 2 & 3 are:
| n | Corners | Sides | Triangles | Total | |
| 0 | Faces | 1 | 3 | 2 | 6 |
| Interior | 0 | 1 | 3 | 4 | |
| Total | 1 | 4 | 5 | 10 | |
| 1 | Faces | 3 | 9 | 6 | 18 |
| Interior | 3 | 10 | 9 | 22 | |
| Total | 6 | 19 | 15 | 40 | |
| 2 | Faces | 9 | 27 | 18 | 54 |
| Interior | 12 | 37 | 27 | 76 | |
| Total | 21 | 64 | 45 | 130 | |
| 3 | Faces | 27 | 81 | 54 | 162 |
| Interior | 39 | 118 | 81 | 238 | |
| Total | 66 | 199 | 135 | 400 |
Comments
1330 = 12 + 32 + 52 + 72 + 92 + 112 + 132 + 152 + 172 + 192.
The simplest geometrical composition of the Polyhedral Tree of Life is one measured by a number that is the sum of the squares of the first 10 odd integers. This number has the following significance vis-à-vis the Tree of Life: constructed from tetractyses, N overlapping Trees of Life have (50N+20) yods, whilst the N-tree (the lowest N Trees of Life) has (50+30) yods. Hence, 26 Trees contain (50×26 + 20 = 1320) yods and the 26-tree has (50×26 + 30= 1330) yods. The extra 10 yods needed to turn the former into the latter correspond to the 10 geometrical elements that make up the axes of the two polyhedra. What is the significance of this number of Trees, apart from 26 being the number value of YAHWEH, the Godname assigned to Chokmah in the Tree of Life? They are the Tree of Life mapping of 26-dimensional space-time required for spinless strings to be consistent with quantum mechanics. E8×E8′ heterotic superstrings possess both 10-d modes of oscillation and 26-d modes (that is what the term 'hybrid' means in this context). The number 1320 is the sum:
720 + 600 = 1320,
where the 144 Polyhedron has 720 geometrical elements and the disdyakis triacontahedron has 600 elements surrounding their axes. The counterpart to this in the 26-Tree is that 14 Trees have (14×50 + 20 = 720) yods, the 14-tree has 730 yods and the next 12 Trees above it have (12×50=600) more yods. This 14:12 division in the 26-tree is analogous to how the 144 Polyhedron is constructed from other Catalan solids. We start with the rhombic dodecahedron (14 vertices, 24 edges, 12 rhombic faces), stick rhombic pyramids to each of its 12 faces to generate the disdyakis dodecahedron with (12+14=26) vertices, (24 + 4×12 = 72 edges) and (4×12=48) faces, and then stick tetrahedra to these faces to generate the (26+48=74) vertices, (72 + 3×48 = 216) edges and (3×48=144) faces of the 144 Polyhedron. Notice that we start with a polyhedron with 14 vertices and add 12 vertices to generate the 26 vertices of the disdyakis dodecahedron. This is a Catalan solid with the 1:3:2 proportion of the number of vertices, edges & faces surrounding its axis. Therefore, its geometrical composition is determined by the table of weights shown above, so that there are (10×24=240) geometrical elements surrounding its axis. The 144 Polyhedron has 720 elements surrounding its axis. This 240→720 change is analogous to the 240 hexagonal making up the seven Type A polygons of the inner Tree of Life and their 720 yods surrounding their centres when they are Type B. The existence of the correspondences:
14-tree ↔ 720 yods ↔ 720 geometrical elements of the 144 Polyhedron;
12 Trees ↔ 600 yods ↔ 600 geometrical elements of the disdyakis triacontahedron;
26 Trees ↔ 1320 yods ↔ 1320 geometrical elements of the Polyhedral Tree of Life
is a sign that this pair of polyhedra constitutes the polyhedral version of the Tree of Life and encodes the physics of E8×E8 heterotic superstrings. Nothing more than that is being claimed here, for one correlation on its own does not amount to conclusive evidence.
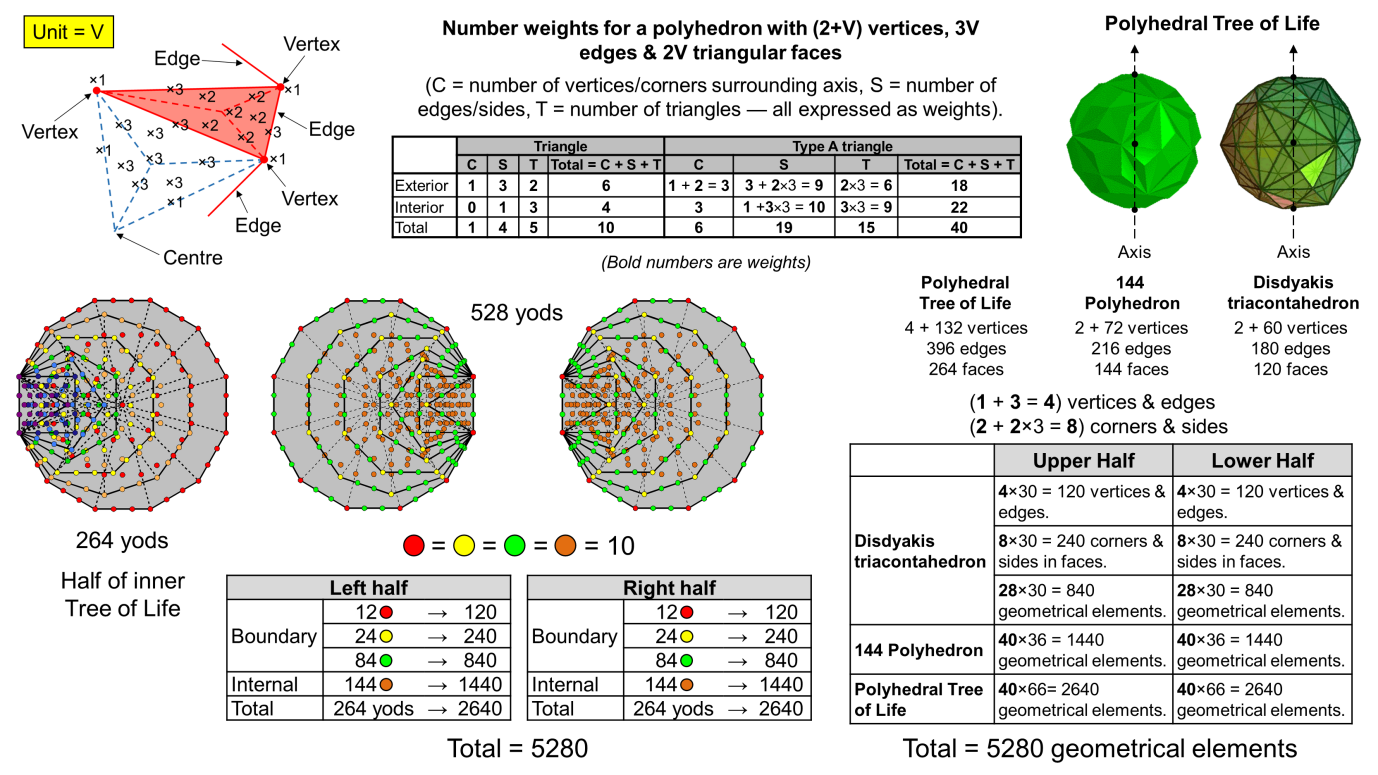
yod generates the numbers of geometrical elements in each half of both polyhedra. Each upper/lower half of the pair of polyhedra with 2640 geometrical coresponds to each half of the inner Tree of Life with 264 yods, the 120:144 boundary:interior distinction for yods in the latter corresponding to the 1200:1440 difference between the geometrical compositions of the disdyakis triacontahedron and the 144 Polyhedron. This correlation is spectacular evidence that they constitute the polyhedral version of the polygonal inner Tree of Life. It is discussed in detail on page 15 of Sacred geometry/Polyhedral Tree of Life.
2400 = 720 + 1680.
Furthermore, the number weight for vertices & edges is 4, so that the weight for other corners & sides in faces is (12−4=8). This means that the 720 corners & sides in faces comprise (4×60=240) vertices & edges and (8×60=480) corners & sides, i.e.,
720 = 240 + 480.
Compare this with the fact that E6 has as a subgroup the rank-4 exceptional group F4 of order 48, so that its associated 48 gauge fields have 480 components. Finally, the 480 corners & sides include (2×60=120) corners of sectors in faces. Compare this with the fact that F4 contains G2, the smallest exceptional group, which is of order 12. The largest exceptional subgroup in E8 is the rank-7 E7 with order 126. It has 54 more roots than E6. As 540 = 60×9, a number weight of 9 not including the weight of 12 that corresponded to E6 generates this number. There are 540 geometrical elements that are either triangles in faces or internal corners. Alternatively, there are 540 internal triangles. The five exceptional groups:
G2 ⊂ F4 ⊂ E6 ⊂ E7 ⊂ E8
have orders:
12, 48, 72, 126, 240
which, multiplied by 10, generate various subsets of the 2400 geometrical elements in the disdyakis triacontahedron with Type A faces and internal triangles. Here is a summary in terms of number weights:
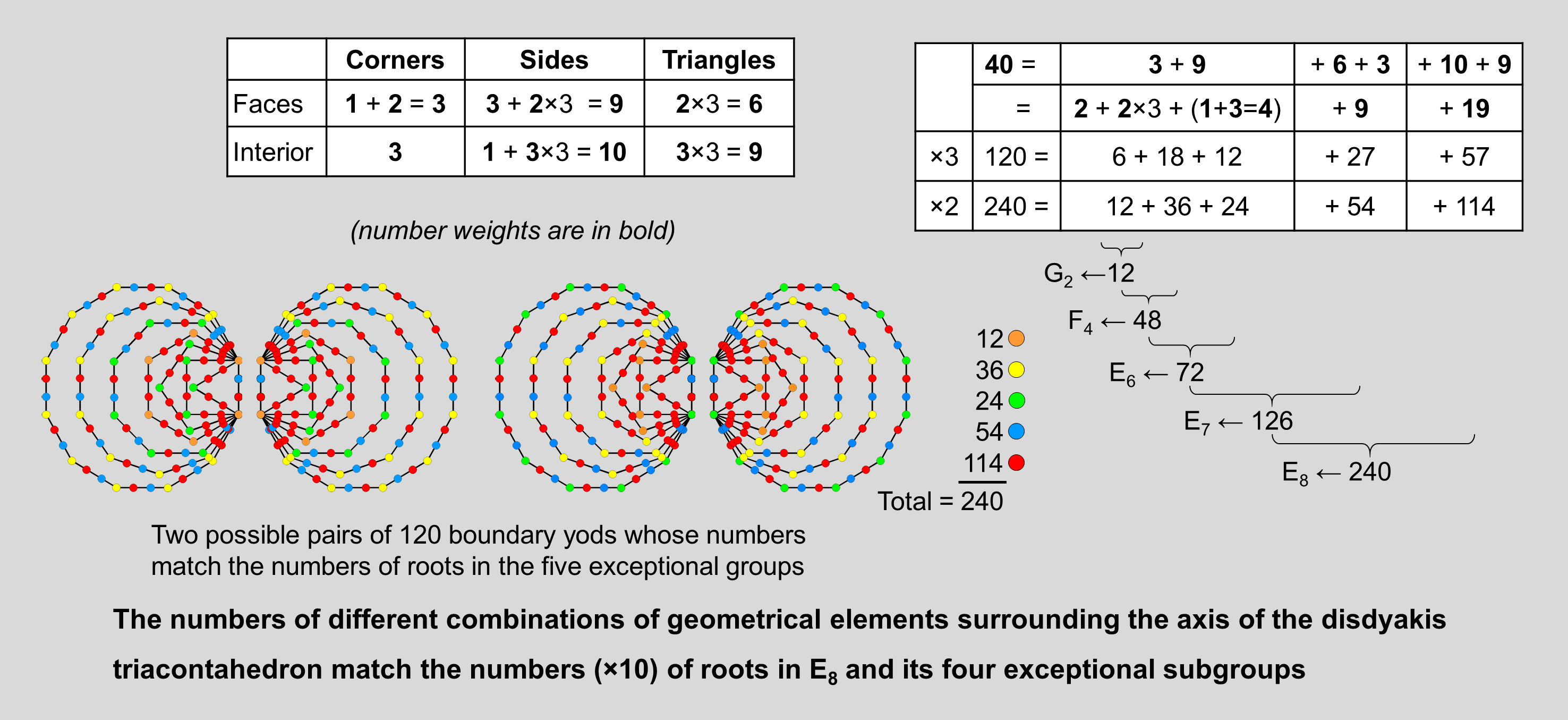
The multiplying factor of 3 refers to the 30 vertices in each half of the disdyakis triacontahedron that surround its axis (the factor of 10 is suppressed for the sake of clarity) and the factor of 2 refers to these two halves.
The diagram displays two possible patterns of the 240 yods lining the sides of the two separate sets of seven enfolded polygons.
The issue of which pattern is correct need not detain us here because the crucial point is that the geometry of the boundary of the inner Tree of Life is able to match not only the root structure of E8 and its exceptional subgroups but also the various combinations of geometrical elements making up the disdyakis triacontahedron composed externally and internally of Type A triangles.
The number weights for the yod populations of a polyhedron with (2+V) vertices, 3V edges & 2V nth-order triangular faces are tabulated below:
Number weights for nth-order triangular faces and internal triangles
| Corners | Hexagonal yods | Total | ||
| Sides | Central | |||
| Faces | 3n | 2×3n+1 | 2×3n | 3n+2 |
| Interior | ½(3n+1 − 3) | 3n+2 − 7 | 3n+1 | ½(3n+3 − 17) |
| Total | ½(5×3n − 3) | 5×3n+1 − 7 | 5×3n | ½(5×3n+2 − 17) |
Their values for n = 0, 1, 2 & 3 are:
| n | Corners | Hexagonal yods | Total | ||
| Sides | Central | ||||
| 0 | Faces | 1 | 6 | 2 | 9 |
| Interior | 0 | 2 | 3 | 5 | |
| Total | 1 | 8 | 5 | 14 | |
| 1 | Faces | 3 | 18 | 6 | 27 |
| Interior | 3 | 20 | 9 | 32 | |
| Total | 6 | 38 | 15 | 59 | |
| 2 | Faces | 9 | 54 | 18 | 81 |
| Interior | 12 | 74 | 27 | 113 | |
| Total | 21 | 128 | 45 | 194 | |
| 3 | Faces | 27 | 162 | 54 | 243 |
| Interior | 39 | 236 | 81 | 356 | |
| Total | 66 | 398 | 135 | 599 | |
Only the case n = 0 will be discussed here. The case n = 1 is analysed here in "#7 The 144 Polyhedron."
Comments
The number weight for the total number of yods in the polyhedron with 0th-order triangles as
faces and internal triangles is 14. This means that the 144 Polyhedron has (14×72=1008) yods
surrounding its axis, 504 being in each half, and the disdyakis triacontahedron has 840 such yods. The latter
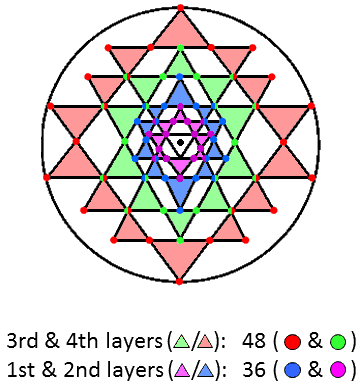
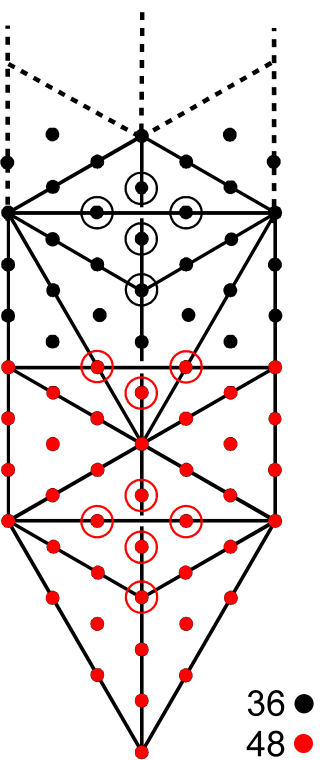
comprise (6×60=360=36×10) corners & hexagonal yods at centres of (5×60=300) tetractyses and
(8×60=480=48×10) hexagonal lining their sides. This 48:36
division is highly significant because it is characteristic of sacred geometries. For example, it manifests
in:
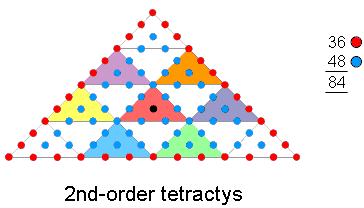 |
 |
 |
|
48:36 patterns in the 2nd-order tetractys, the 3-d Sri Yantra & the 1-tree. |
||
It appears also in the 84 hexagonal yods lining the sides of the seven enfolded polygons of the inner Tree of Life as the 36 hexagonal yods lining the triangle, hexagon & dodecagon and the 48 hexagonal yods lining the four other polygons (several other combinations of polygons display the same 36:48 pattern). There are 84 subplanes/Trees of Life in CTOL above the physical plane/7-tree (this is what the 84 yods surrounding the centre of the 2nd-order tetractys symbolise — see here). In the context of the micro-psi observations by Annie Besant & C.W. Leadbeater of the basic consituents of matter, discussed in Occult Chemistry, the number (840) of yods in the disdyakis triacontahedron appears as the 840 1st-order spirillae in each half of a whorl of the UPA. A whorl twists fives time around the spin axis of the UPA, so there are 84 1st-order spirillae in every ¼-revolution — on average, at least. There are 840 spirillae in every 2½ revolutions, that is, in each outer or inner half of a whorl. As
292 − 1 = 3 + 5 + 7 +... + 57 = 840,
the number 840 is the sum of the first 28 odd integers after 1. But 292 − 1 = (29−1)(29+1) = 28×30 = 14×60, where 14 is the number weight for the yod population and 60 is the number of vertices of the disdyakis triacontahedron that surround its axis. Here is the arithmetic factorisation of 840 that manifests in the yod population of the disdyakis triacontahedron with tetractyses as its faces and internal triangles. There is always harmony between number and sacred geometry. Indeed, it is as though the latter were the spatial manifestation of the former or, to be specific, of certain archetypal numbers. One of them is 840, which is a structural parameter of the subquark state of the E8×E8 heterotic superstring described by Besant & Leadbeater with the use of the yogic siddhi called "anima."
The analysis of the Platonic solids in Superstrings as sacred geometry/Platonic solids reveals that, when their faces and internal triangles are Type A (i.e., when they are divided into their sectors), the tetrahedron, octahedron & cube, collectively, have 840 geometrical elements surrounding their axes, as do, separately, the icosahedron and the dodecahedron (see page 5). This is another illustration of the archetypal character of the number 840. Sceptics of the paranormal need to ask themselves the following question: how could this number, which quantifies the geometrical compositions of not just one but three groups of Platonic solids, appear at the heart of the micro-psi description of the basic constituent of the nuclei of atoms? Are they really willing to believe that it is just chance? If that seems too implausible even to them (which, of course, it is!), what alternative do they have other than to accept the claim that sacred geometries embody archetypal numbers which manifest throughout the universe in the form of vibrating superstrings — particles which were accurately described by two people who were totally unaware that numbers like 840 and 1680 are global parameters of the geometry of the Platonic solids but yet whose purported, paranormal descriptions contain these numbers?
| << Previous 1... 14 15 16 [17] 18 Next >> |