ARTICLE 45

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://www.smphillips.mysite.com

Abstract 

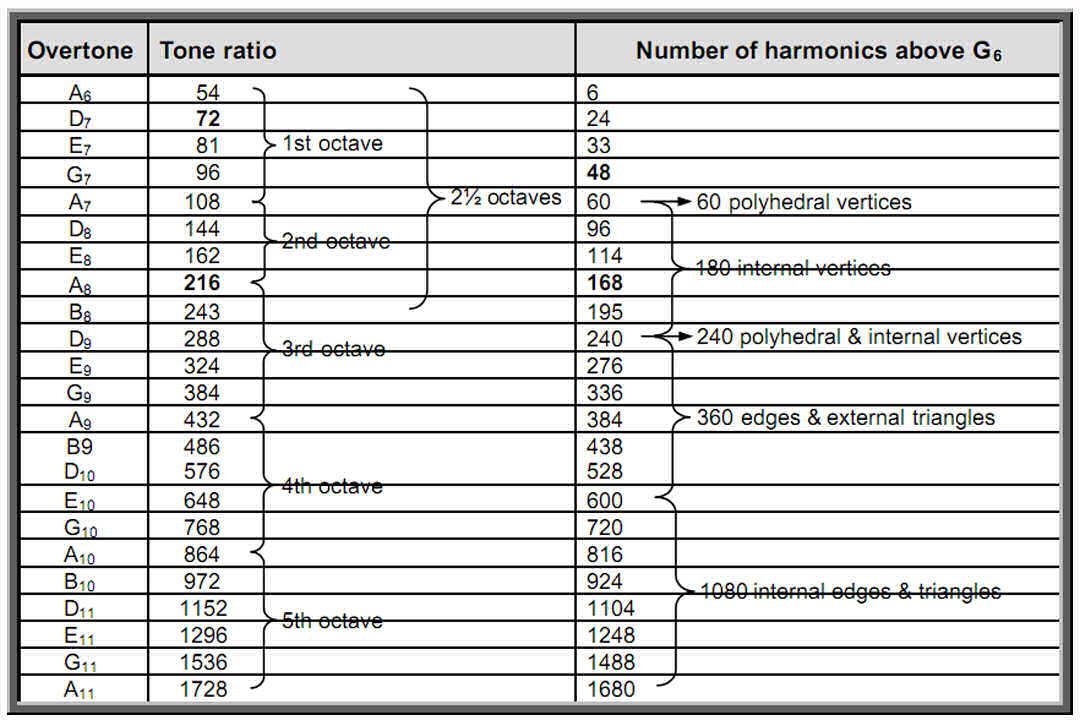
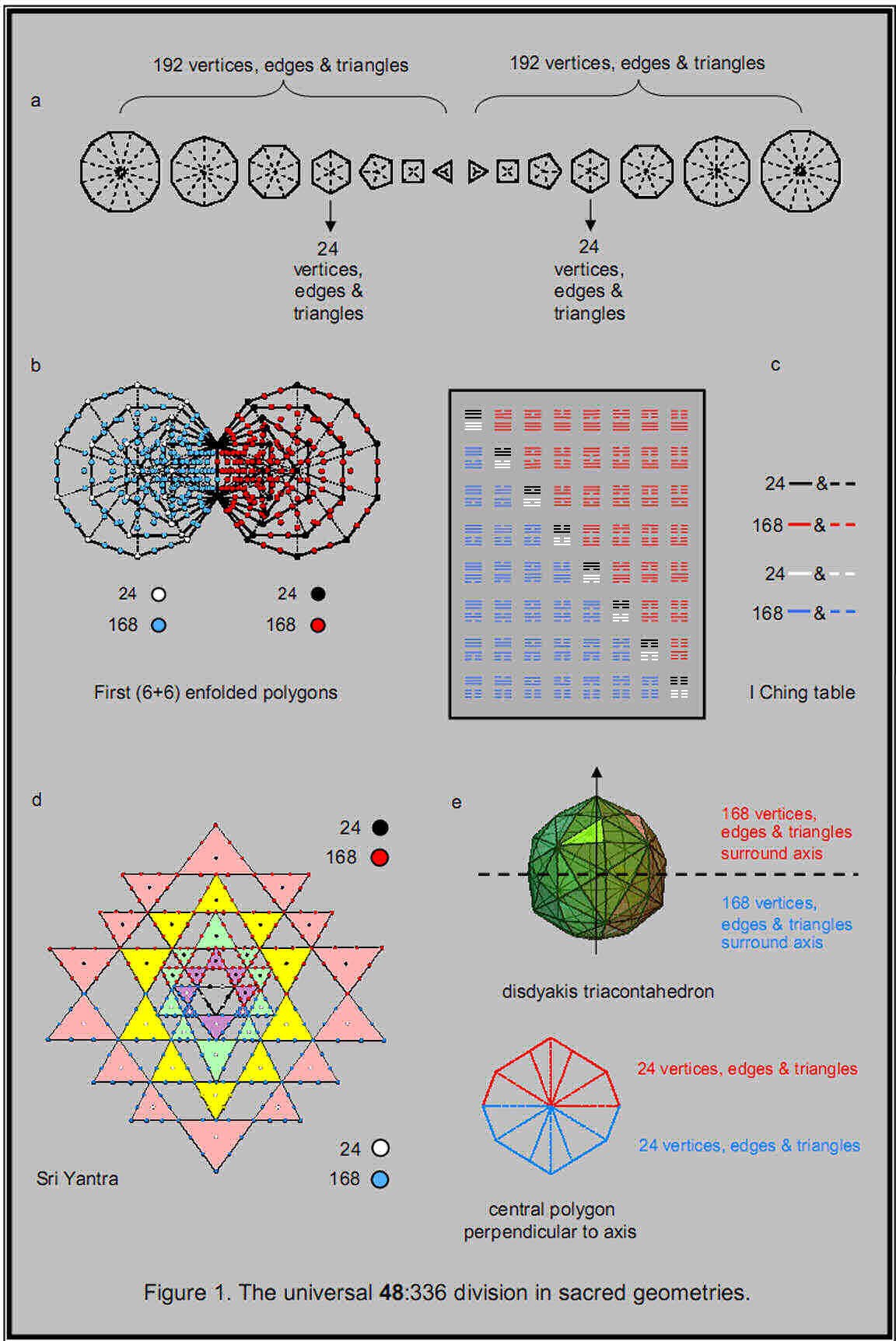
1

2

1. The holistic 48:336 pattern in the Pythagorean musical scale

As discussed in previous articles, the divisions:

384 = 48¹ + 168 + 168

and

48 = 24 + 24

are found in the geometrical composition of the 14 separate polygons of the inner Tree of Life (Fig. 1a), the first (6+6) enfolded polygons (Fig. 1b), the I Ching table (Fig. 1c), the Sri Yantra (Fig. 1d) and the disdyakis triacontahedron (Fig. 1e). This is because they embody the universal blueprint of holistic systems. This article will explain the musical significance of these divisions.

Table 1 displays the first 15 octaves of the Pythagorean musical scale:

Table 1. Tone ratios of the first 15 octaves of the Pythagorean musical scale.
(overtones are in grey cells)

G₅, the perfect fifth of the fifth octave, the tenth overtone, the 33rd note and the 11th Pythagorean harmonic,² has a tone ratio of 24. G₆, the perfect fifth of the sixth octave, the 40th note and the 15th Pythagorean harmonic, has a tone ratio of 48. The Pythagorean Tetrad expresses both tone ratios because 

10 = 1 + 2 + 3 + 4,

33 = 1! + 2! + 3! + 4!,

24 = 1×2×3×4

and

40 = 4 + 8 + 12 + 16,

whilst 15 is the number of combinations of four objects, taken 1, 2, 3 & 4 at a time. The 26th Pythagorean harmonic is A₈ with tone ratio 216 (the number value of Geburah). Therefore, YAH, the Godname of Chokmah with the gematria number value 15 (see list of Godname numbers in endnote 1) prescribes G₆, up to which there are 48 harmonics (15 Pythagorean) and YAHWEH, the complete Godname of Chokmah with number value  26, prescribes A₈, up to which there are 216 harmonics, i.e., 168 extra harmonics. The note G₉, the perfect fifth of the

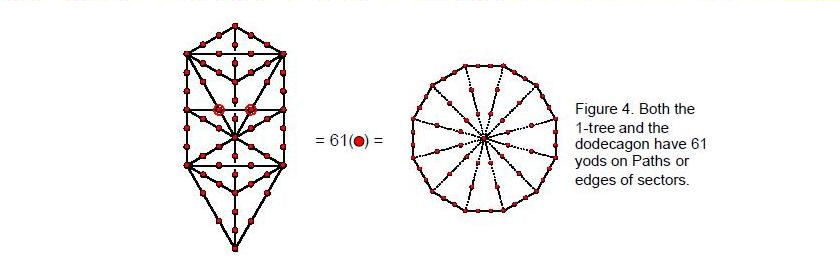
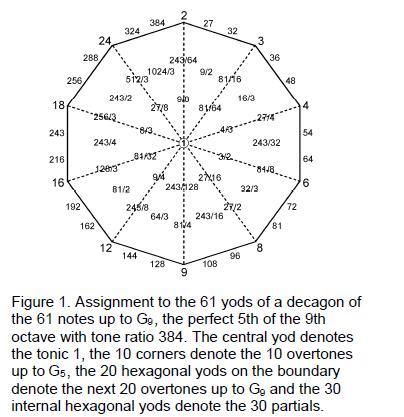
3

ninth octave, has the tone ratio 384. It is the 30th overtone. EL, the Godname of Chesed with number value 31, prescribes this note as the 31st Pythagorean harmonic and as the 61st note, 61 being the 31st odd integer. The value 1 of the letter E (aleph) denotes the tonic and the value 30 of the letter L (lamed) denotes the 30 overtones up to G₉. As the Pythagorean measure of wholeness and perfection, the number 10, or Decad, defines the 61 notes up to G₉ because, constructed from tetractyses, the 10-sided decagon has 61 yods (Fig. 1). The central yod denotes the tonic, the 30 internal yods surrounding it denote the 30 partials up to G₉ and the 30 boundary yods denote the 30 overtones, the yods at the ten corners denoting the ten overtones up to G₅. The Decad also defines the 26th Pythagorean harmonic A₈ as the 55th note, where

55 = 1 + 2 + 3 + ... + 10.

This geometrical correspondence is evidence that the 60 note intervals above the tonic up to G₉  constitute a holistic set. These 60 degrees offreedom are symbolized in the tetractys-constructed TOL by its 60 hexagonal yods symbolizing Sephiroth of Construction, in the dodecagon by its 60 hexagonal yods, in the triakis tetrahedron by the 60 vertices, edges & triangles surrounding an axis joining two opposite vertices and in the disdyakis triacontahedron by the 60 vertices surrounding an axis joining two opposite vertices. The Tetrad also defines the 61 notes up to G₉ because they can be assigned to the 61 yods in a Type B square. In fact, they are the counterpart of the 61 sounds that can be created by playing the 15 notes of the Greater Perfect System known to the ancient Greeks — another holistic system. The 31 sounds (notes, harmonic intervals & chords) made by playing the eight notes of the first octave in the Greater Perfect System correspond to the 31 harmonics; the 30 sounds created by playing the second octave correspond to the 30 partials.

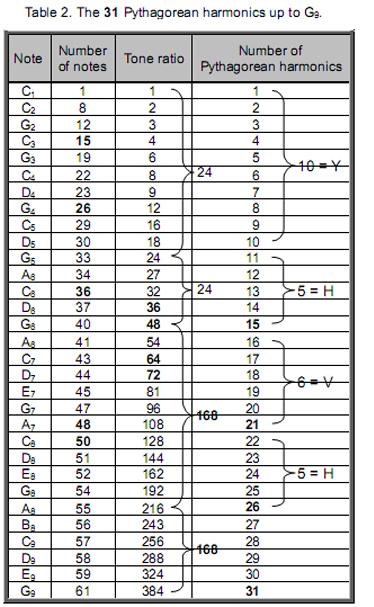
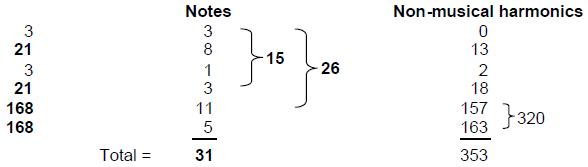
Table 2 displays the 31 harmonics of the Pythagorean scale up to G₉. YAH (YH) separates the 48 harmonics up to G₆ from the next 336 harmonics up to G₉, which is prescribed by EL. The last 168 harmonics with five notes are differentiated by the Godname YAHWEH. The number 10 of yod (Y) and the number 5 of heh (H) divide the 48 harmonics into two sets of 24. The 48 harmonics contain 15 notes prescribed by YAH. The first set of 168 harmonics up to A₈ contains 11 notes — the sum of the remaining numbers of the letters vau and heh of YAHWEH — and 157 non-musical harmonics. The second set of 168 harmonics up to G₉ contain five notes and 163 non-musical harmonics. Of the 336 harmonics, 16 are notes and 320 are non-musical harmonics. Of the 384 harmonics, 31 are notes and 353 are non-musical harmonics. Of the former, 22 are notes other than octaves. As 22 is the 21st odd integer after 1, EHYEH with number value 21 prescribes the overtones up to G₉ that are not octaves. It also prescribes G₉ because this is the 21st note above G₆. Of the 61 notes, 52 notes are not octaves. 52 is the 26th even integer, showing how YAHWEH prescribes the archetypal set of notes up to G₉.

The 24:24:168:168 division of harmonics in the Pythagorean scale is the musical manifestation of the various sacred geometries displayed in Fig. 1. What confirms that these 48:336, 168:168 and 24:24 subdivisions have significance is that they are prescribed by the Godnames YAH, YAHWEH and EL and their letter values. This cannot be plausibly attributed to chance. The 384 harmonics up to G₉ consist of the fundamental C₁ and 383 higher harmonics. Amazingly, 383 is the 76th prime number, showing how the Godname YAHWEH ELOHIM with number value 76 prescribes the first 61 notes of the Pythagorean scale spanning 384 harmonics.

4 

The number 383 appears in the 10-tree (Fig. 2), whose 65 SLs are prescribed by ADONAI, Godname of Malkuth with number value 65. The 10-tree has been shown in many previous articles to embody structural and dynamical parameters of the E₈×E₈ heterotic superstring. 383 hexagonal yods are at the centres of all the tetractyses that have 1680 yods below the 65th SL, the top of the tenth Tree of Life.³ The latter symbolize the 1680 turns of a helical whorl of the heterotic superstring (Fig. 3). In other words, these 1680 

yods comprise 383 yods of the type that symbolize Malkuth. This will prove to be highly significant when we find later the harmonic counterparts of the former.

ELOHIM with number value 50 prescribes the 50 notes other than the 11 musical harmonics up to G₅, the perfect fifth with tone ratio 24. The first ten overtones and the 22 partials up to G₅ were shown in Article 12⁴ to constitute a Tree of Life pattern because they are the counterpart of the ten Sephiroth and the 22 Paths. The 11:50 division of the 61 notes corresponds in the tetractys-constructed 1-tree to the 11 corners of its 19 triangles and to the 50 hexagonal yods lying on their 25 edges (Fig. 4). The number 61 creates the

shape of the 1-tree as the number of yods lining the edges of its triangles. Its counterpart in the tetractys-constructed dodecagon are the 61 yods on edges of tetractyses. The counterpart of the 11-50 division in the decagon are the 11 corners of tetractyses and its 50 hexagonal yods. Its counterpart in the disdyakis triacontahedron are the centre of the polyhedron, the ten B vertices and the 50 A & C vertices surrounding a B-B axis. The 20 C vertices correspond to the 20 hexagonal yods lying on the ten edges of triangles in the trunk of the 1-tree; the 30 A vertices correspond to the 30 hexagonal yods lying on the 15 edges making up its branches. The musical counterparts of the 20 C vertices, the ten B vertices and the 30 A vertices are, respectively, the 20 partials in the first four octaves, the ten remaining partials and the 30 overtones. The centre of the polyhedron denotes C₁, the fundamental. The disdyakis triacontahedron is the polyhedral representation of the 60 notes above the tonic up to G₉, the 384th harmonic and the 31st overtone.

The division:

24 = 3 + 21

found in sacred geometries manifests in the Pythagorean scale, firstly, as the three harmonics (all notes) up to G₂ (see Table 1) and the 21 higher harmonics (eight notes, 13 non-musical harmonics) up to G₅ and, secondly, as the three harmonics (one note, two non-musical harmonics) beyond G₅ up to the next note A₅ and the 21 harmonics (three notes, 18 non-musical harmonics) beyond that up to G₆. The

5

(3+3=6) harmonics comprise four notes and two non-musical harmonics; the (21+21=42) harmonics comprise 11 notes and 31 non-musical harmonics. The composition of the 384 harmonics is shown below:

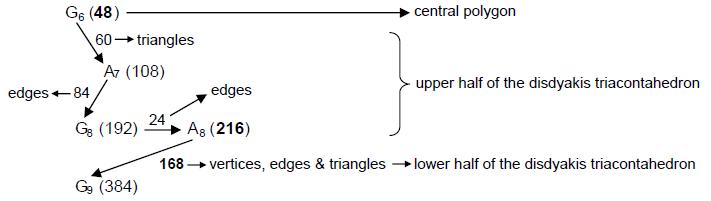
Its 31 musical harmonics comprise every type of note except perfect fourths.

Twenty-four vertices, 84 edges & 60 triangles of the disdyakis triacontahedron are above or below the 48 geometrical elements surrounding the centre of its central, 12-sided polygon perpendicular to an A-A axis. Compare these geometrical compositions with the composition of harmonics:

Starting from G₆, the 15th musical harmonic with tone ratio 48, there are 60 more harmonics up to A₇, the 21 st musical harmonic, then 84 more harmonics up to G₈ and 24 more harmonics up to A₈, the 26th musical harmonic. The composition of the 168 geometrical elements either above or below the central polygon of the disdyakis triacontahedron matches the 168 harmonics between G₆ and A₈, making it too implausible that the correspondence between the geometry and the notes of the Pythagorean scale could be coincidental. As the 48 geometrical elements of the polygon correspond to the 48 harmonics up to G₆, this note prescribed by YAH corresponds to the central polygon, whilst the note A₈ prescribed by YAHWEH corresponds to half of the polyhedron with 216 geometrical elements. The 168 harmonics beyond A₈ up to G₈ correspond to the 168 geometrical elements in the other half of the polyhedron below the polygon. Each element is a manifestation of a harmonic, the 336 harmonics between G₆ and G₉ being the musical counterpart of the 336 geometrical elements above and below the central polygon.

The Tetrad Principle expresses the 384 harmonics because

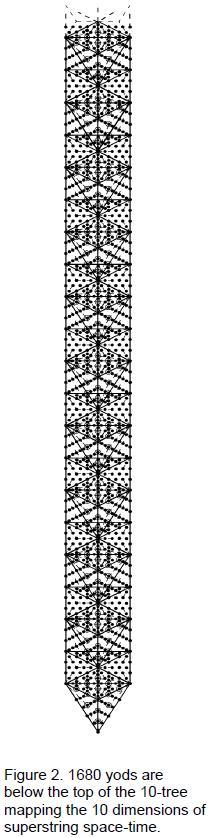
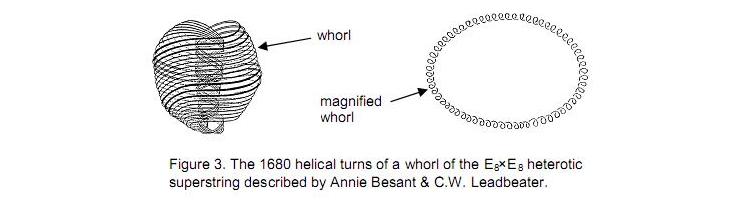
They include (4²=16) octaves and perfect fifths. The 378 geometrical elements above and below the 48 elements of the central polygon are the geometrical counterpart of the 378 harmonics above G₆. They contain (4²=16) overtones. The 48 harmonics up to G₆ contain 15 Pythagorean harmonics, where 15 is the fourth triangular number after 1. The three harmonics up to G₂ and the three harmonics above G₅ to A₅ comprise four Pythagorean harmonics (1, 2, 3 & 27).

The Decad determines the 384 harmonics because not only is the 384th harmonic the last of the notes that can be assigned to the 61 yods in a decagon with tetractyses as sectors but also there are 120 notes and successive intervals up to G₉, where 120 is the sum of the first ten odd integers after 1:

121 = 11² – 1 = 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 .

The Godname EHYEH prescribes G₉ because its number value 21 is the last of these odd integers.

2. The 1680 harmonics

Inspection of Table 1 reveals that there are 1680 harmonics between note G₆ with tone ratio 48 and note A₁₁ with tone ratio 1728. This is the 76th note. YAHWEH ELOHIM with number value 76 prescribes the very note in the Pythagorean scale that is separated by 1680 harmonics from G₆. This amazing fact

6

demonstrates how YAHWEH ELOHIM prescribes the superstring structural parameter 1680 as well as the structural parameter 336! The Godname ELOHA with number value 36 prescribes A₁₁ as the 36th note above G₆, the 48th harmonic. The Tetrad aptly determines A₁₁ because it is the 44th musical harmonic. Moreover, there are ten (=1+2+3+4) octaves, ten perfect fifths and 24 (=1×2×3×4) other Pythagorean harmonics up to A₁₁. This note is the only overtone other than A₈ and G₉ that is separated from G₆ by an integer multiple of 168. Examination of the notes in Table 1 confirms that the first note to have a tone ratio larger than 1680, namely, A₁₁, is also the only note differing by 1680 harmonics from a note of lower pitch! The note A₁₄ is the last note to differ from its predecessor by less than 1680 harmonics, whilst all subsequent, consecutive notes differ by more than 1680 harmonics. G₆ and A₁₁ are therefore the only notes in any octave of the Pythagorean scale whose tone ratios differ by 1680. Demonstration of the uniqueness of this pair of notes is important because it eliminates the criticism that any discussion based upon a particular choice of pairs of notes would be ad hoc if other pairs existed that differed by 1680 harmonics.

The uniqueness of A₁₁ become significant in the context of the 1680 turns of the helical whorl of the heterotic superstring, whose embodiment in the inner form of ten Trees of Life shows that they consist of ten sets of 168 turns. Its connection to superstring physics is further demonstrated by the fact that, as the 75th note above the fundamental, A₁₁ is the 65th note other than the ten octaves, i.e., it is prescribed by ADONAI, Godname of Malkuth with number value 65. A₁₁ is the 33rd overtone other than octaves, where 33 = 1! + 2! + 3! + 4!. The 33rd note and the tenth overtone is G₅ with tone ratio 24. Therefore, A₁₁ is the 33rd non-octave overtone above the 33rd note! Given that there are 1680 yods in the 33-tree, the role played by the number 33 in each context in determining the superstring structural parameter 1680 is remarkable. The 50th note prescribed by ELOHIM is the seventh octave C₈ with tone ratio 128. It is 80 harmonics above G₆, so that the next 26 notes prescribed by YAHWEH up to A₁₁ span 1600 harmonics. The two words in the Godname of Tiphareth define a 80:1600 division in the number 1680 that appears in the 33-tree as the 80 yods in the 1-tree and as the 1600 yods in the 32 Trees of Life above it. This section of CTOL is prescribed by ADONAI because Malkuth of the 33rd TOL is the 65th SL on the central pillar. There are 1730 yods up to the top of the 34th TOL, that is, 1728 yods below it other than its Daath. Alternatively, there are 48 yods below the top of the 34th TOL other than its Daath that are outside the 33-tree. This 48:1728 distinction is the TOL counterpart of the 48 harmonics up to G₆ and the 1728 harmonics up to A₁₁. Each yod denotes a harmonic. The 48 harmonics from G₆ to G₇ are the counterpart of the 48 yods up to Chesed of the 1-tree. The 80 harmonics from G₆ to C₈ are the counterpart of the 80 yods of the 1-tree. The first of the 1680 harmonics is the 49th, so that it is prescribed by the Godname EL CHAI of Yesod.

None of the 14 types⁵ of notes in the seven musical scales:

1        256/243       9/8       32/27       81/64         4/3       1024/729        729/512        3/2       128/81        27/16        16/9        243/128        2

has a higher octave whose tone ratio is 1680. This number must be understood as referring, not to a note of any scale, but to the number of harmonics between G₆ and A₁₁. Systematic examination of the notes shown in Table 1 confirms that the first note to have a tone ratio larger than 1680 — A₁₁ — is also the only note differing by 1680 harmonics from a note of lower pitch! The note A₁₄ is the last note to differ from its predecessor by less than 1680 harmonics, whilst all subsequent, consecutive notes differ by more than 1680 harmonics. G₆ and A₁₁ are therefore the only notes in any octave of the Pythagorean scale whose tone ratios differ by 1680. The uniqueness of this pair of notes is highly significant because it eliminates the criticism that any discussion based upon a particular choice of pairs of notes would be ad hoc if other pairs existed that differed by 1680 harmonics.

The 1680 harmonics from G₆ to A₁₁ contain 29 overtones. 29 is the tenth prime number. The Pythagorean Decad defines how many of these harmonics are musical notes. Table 1 shows that they contain 24 overtones other than octaves. Counting from G₆, we see that the 1680th harmonic is the 24th Pythagorean harmonic other than octaves. The first 168 harmonics up to A₈ include nine such notes, the next 168 harmonics up to G₉ include four such notes and the remaining harmonics include 11 notes that are not octaves. The 24 non-octave overtones are distributed nine to the first 168 harmonics and 15 to the remainder. This 9:15 division reminds us of the distinction in string theory between the nine transverse dimensions existing in the 11-dimensional space-time of M-theory and the 15 higher transverse dimensions belonging to bosonic strings in 26-dimensional space-time. If we take the analogy seriously, it suggests that oscillations in the 24 transverse directions generate 24 particles as 24 vibration modes that correspond to the 24 overtones, the nine overtones up to A₈ corresponding to the nine particles representing Kaluza-Klein-type oscillations in each of the nine transverse dimensions and the 15 remaining overtones corresponding to the 15 vibration modes for the 15 higher dimensions. Are the 1680 helical turns of a closed whorl the manifestation of the charge sources of 24 gauge fields of E_8, the ten whorls of the E₈×E₈ heterotic superstring being the manifestation of the charge sources of the 240 gauge

7

fields associated with its 240 roots? The musical analogy strongly implies such an interpretation, although it should be emphasized that the parallel between these holistic systems should be taken not literally but as a pointer to the underlying physics of the heterotic superstring.

When G₆ is regarded as the fundamental frequency, the tone ratios of the 24 higher overtones other than octaves are shown below:

The overtones span exactly five octaves, the last note A₁₁ having the new tone ratio 36 relative to G₆. The set of 24 overtones is prescribed by ELOHA, Godname of Geburah with number value 36. The note with tone ratio 36 is D₆. It is the 36th note above the tonic. Indeed, it is the only note in the scale whose tone ratio is identical to its position number above the tonic — another reason why A₁₁ is special.

There are three overtones up to the note A₈ with tone ratio 216 that remain overtones when G₆ is the fundamental. The remaining 21 overtones comprise A₆, the first one, five partials up to A₈, followed by ten harmonics and five partials spanning the last three octaves. These are the letter values of EHYEH (AHIH): A = 1, H = 5, I = 10 & H = 5. In terms of its geometrical counterpart in the disdyakis triacontahedron, A₈ represents the last of the 216 geometrical elements constituting half of the polyhedron. It is the reason for the thick, vertical line dividing the 24 overtones at this note. The 24 overtones display the 3:21 division characteristic of holistic systems, as demonstrated in Article 40.⁶

Table 3. The 1680 harmonics between G₆ and A₁₁.

Just as the 1680 helical turns of each whorl of the heterotic superstring revolve five times around its axis of spin, so the 1680 harmonics between G₆ with tone ratio 54 and A₁₁ with tone ratio 1728 contain 24 overtones other than octaves spanning five complete octaves, that is, five musical cycles. In both cases, the number 1680 displays a five-fold development. The relative frequencies of the 24 overtones increase by a factor of 2⁵ = 32 (=1728/54). This is the number of components of the wave function describing spin–½ fermions in 10-dimensional space-time. A remarkable analogy exists between the vibrating, string-like whorl and the harmonics of the Pythagorean scale because they are both holistic systems described by the same mathematical archetypes.

8

Let us next compare the pattern of 1680 harmonics with the 1680 geometrical elements surrounding an axis of the disdyakis triacontahedron passing through two diametrically opposite vertices.⁷ If the former truly constitute a holistic set, their composition should correlate with the geometrical structure of this polyhedron. The elements comprise 24 vertices above the central polygon, 24 vertices below it, 12 vertices of the central polygon and 180 vertices of the 540 internal triangles, i.e., 240 vertices. Their musical counterparts are the 24 harmonics up to D₇ (Table 3), then 24 harmonics up to G₇, 12 more harmonics to A₇ (the first of the five octaves and the 21st Pythagorean harmonic) and the next 180 harmonics up to D₉, which, as the perfect fourth of the third of these octaves, is the middle of the five octaves. Then there are 180 edges, 60 internal edges ending on polyhedral vertices & 120 external triangles, i.e., 360 edges & triangles. Their counterpart is the 360 harmonics beyond D₉ up to E₁₀. Finally, there are 540 more internal edges of 540 internal triangles, i.e., 1080 internal edges & triangles. Their counterpart is the 1080 harmonics above D₉ up to A₁₁.

There is no overtone that is the 840th harmonic above G₆. The only two notes that differ by 840 harmonics are G₅ with tone ratio 24 and A₁₀ with tone ratio 864, but they do not all fall within the range of the 1680 harmonics. However, there are 840 odd harmonics from 49 to 1727 and 840 even harmonics from 50 to 1728, showing how the Godname ELOHIM with number value 50 and EL ChAI with number value 49 prescribe, respectively, the set of 840 even harmonics and the set of 840 odd harmonics. The musical counterpart of the 840 helical turns in the 2½ revolutions of an outer half of each whorl and the 840 turns in the 2½ revolutions of its inner half are therefore the 840 even and 840 odd harmonics between G₆, the 15th Pythagorean harmonic, and A₁₁, the 76th note and the 36th note after G₆, showing how YAH, YAHWEH ELOHIM and ELOHA prescribe the five octaves spanned by the 1680 harmonics. Their counterpart in the disdyakis triacontahedron are the 840 vertices, edges & triangles in one half of the polyhedron that surround its axis and their 840 mirror images in its other half.

The 24 overtones in the 1680 harmonics are notes of the first five octaves of the A scale (Hypodorian mode). In terms of this scale, they comprise 12 harmonics and 12 partials with the following tone ratios:

A = 1: lowest octave with tone ratio 2.
H = 5: five octaves of partials (16/9, 32/9, 64/9, 128/9, 256/9).
I = 10: ten overtones (3, 4, 6, 8, 9, 12, 16, 18, 24, 32).
H = 5: five octaves of partials (4/3, 8/3, 16/3, 32/3, 64/3).

The correlation is evidence that EHYEH prescribes the higher dimensions of superstrings themselves. Notice that the letter values Y = 10 & H = 5 of the Godname YAH denote, respectively, the ten overtones and the five octaves of perfect fourths. Notice also that the first ten overtones in the A scale are the same as the first ten overtones in the Pythagorean scale (compare the tone ratios shown above with Table 1). These overtones and the 22 partials up to the tenth overtone were shown in ref. 4 to constitute a Tree of Life pattern. Seven of them (notes B, D & E) belong also to the A scale.

9

Given this correspondence between the letter values of EHYEH and the numbers of overtones and partials in the five octaves of the A scale that they span — a correlation of such detail that it could not plausibly arise by chance — the following question arises: what compactified dimensions correspond to the numbers? Six of them are predicted by superstring theory and 15 are dimensions belonging only to bosonic strings. This division is indicated by the letters A and H of EHYEH (Hebrew: AHIH), which sum to 6, and by the letters I and H, which sum to 15. This means that the ten overtones up to the 24th harmonic and the five octaves of perfect fourths in the A scale have their counterparts in the 15 higher, purely bosonic dimensions. What is the string counterpart of this 10:5 distinction between overtones and partials? It is the role played by ten of the bosonic dimensions when a membrane wraps itself around each of them to generate the ten string-like closed whorls of the UPA/superstring, leaving five other dimensions (this is discussed in Article 2⁸). The dimensional counterparts of the three overtones with tone ratios 3, 4 & 6 create the three major whorls corresponding to the Supernal Triad of the Tree of Life. The counterparts of the remaining seven overtones 8, 9, 12, 16, 18, 24 & 32 create the seven minor whorls that correspond to the seven Sephiroth of Construction. A₁₁, the 1680th harmonic beyond G₆ in the Pythagorean scale, is the fifth octave of the A scale with tone ratio 32. This is its 36th note, prescribed by ELOHA, Godname of Geburah with number value 36. Relative to one another, the three overtones 3, 4 & 6 are the tonic, perfect fourth and octave of the Pythagorean scale, whilst the last seven overtones with tone ratios 8, 9, 12, 16, 18, 24 & 32 form two successive octaves of the tonic, major second and perfect fifth, ending with a third octave. This 3:3:1 pattern is analogous in the outer Tree of Life to the two triads of Sephiroth of Construction (Chesed-Geburah-Tiphareth & Netzach-Hod-Yesod) and Malkuth, to which the seven minor whorls correspond, and in its inner form to the two sets of three polygons (triangle, square, pentagon), (hexagon, octagon, decagon) and the final polygon, the dodecagon. It is also analogous to how the perfect fourth divides the octave into the first three notes with tone ratios in the ratio 1:9/8:(9/8)² and their inversions — the last three notes before the octave with tone ratios in the same proportion. Analogous 1:3:3 divisions are found in the seven musical scales as the Dorian mode, the three authentic modes and the three plagal modes,⁹ in the seven imaginary octonions, whose algebra is represented by the two sets of seven projective elements of the Fano Plane,¹⁰ and in the seven Yang and seven Yin meridians known in acupuncture.¹¹

3. Conclusion

The inner form of the Tree of Life, the I Ching table, the Sri Yantra and the disdyakis triacontahedron display a 48:336 division in their structural components. The musical counterparts of this are the 48 harmonics in the Pythagorean scale up to G₆, the 15th Pythagorean harmonic, and the next 336 harmonics up to G₉, the 52nd note other than octaves prescribed by YAHWEH, the 31st Pythagorean harmonic prescribed by EL, the 21st note above G₆ prescribed by EHYEH and the 383rd note above the fundamental prescribed by the Godname YAHWEH ELOHIM because 383 is the 76th prime number. This Godname also determines the note A₁₁ as the 76th note and therefore the 1680 harmonics between it and G₆. These two notes are the only ones in the Pythagorean scale that are separated by 1680 harmonics. A₁₁ becomes significant in the context of physics because it is prescribed by ADONAI, Godname of Malkuth, as the 65th note other than octaves. It is defined by the Decad because there are 29 overtones between G₆ and A₁₁, where 29 is the tenth prime number. The 24 overtones other than octaves in the 1680 harmonics span five complete octaves of the A scale (Hypodorian mode). As confirmation that these harmonics constitute a holistic set, their composition correlates with the geometrical composition of the disdyakis triacontahedron, shown in previous articles to be the polyhedral Tree of Life. The 240 harmonics up to the middle point of the five octaves correspond to the 240 polyhedral and internal vertices. The 840 even harmonics and the 840 odd harmonics are the musical counterpart of the 840 geometrical elements and their 840 mirror images in each half of the disdyakis triacontahedron that surround an axis joining two opposite vertices. The classes of overtones and partials in the five octaves correlate with the letter values of the Godname EHYEH, supporting the view that a correspondence exists between the 24 transverse dimensions predicted by string theory and the 24 overtones in the 1680 harmonics. The overtones are the musical counterpart of oscillations in these dimensions. The five octaves that they span are the musical counterpart of the five revolutions of each whorl in the E₈×E₈ heterotic superstring — a standing wave with 1680 circularly polarized oscillations, the 840 oscillations that take place in the inner and outer halves of each whorl corresponding to the 840 even harmonics and the 840 odd harmonics. The 22 even overtones are the counterparts of the 22 compactified dimensions, which are, themselves, the physical counterpart of the 22 Paths of the Tree of Life. The lowest octave corresponds to the dimensional segment between the two space-time sheets occupied by superstrings of ordinary and shadow matter. The 21 higher overtones in the Pythagorean scale correspond to the 21 compactified dimensions of these sheets. The numbers of overtones and partials that they form as an A scale are the letter values of EHYEH, Godname of Kether. The last seven overtones divide into two triplets and a single one. This 3:3:1 division is characteristic of all holistic

10

systems, being the archetypal manifestation of the two triads of Sephiroth of Construction and Malkuth in the Tree of Life.

References

1. The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). They have number values obtained by the practice of gematria, wherein each letter of the Hebrew alphabet has a number assigned to it, giving a number value to a word that is the sum of the values of its letters. The Hebrew names, their translations and their number values are shown in the table below:

Gematria number values of the Sephiroth, their Godnames, Archangels, Orders of Angels & Mundane Chakras.

(All numbers from this table that are referred to in the text are written in  boldface ).

2. As the fundamental, the tonic with tone ratio 1 is the first harmonic. Overtones are notes of the Pythagorean scale whose tone ratios are integers. They are referred to in this article as ‘Pythagorean harmonics.’ Non-Pythagorean harmonics, i.e., harmonics that are not notes of any octave of this scale, are referred to simply as harmonics.

3. Proof: there are seven triangles in the kite shape at the bottom of the Tree of Life with Tiphareth as its apex. Above it are 12 triangles in successive Trees of Life. The number of triangles in the n-tree (n an integer) is T(n) = 12n + 7. They have 3×(12n+7) = 36n + 21 sectors. The 127 triangles in the 10-tree have 381 sectors. When these sectors are turned into tetractyses, there is a hexagonal yod at the centre of a tetractys below the apex of the 10-tree and outside it on either side of the central Pillar of

11

           Equilibrium. The number of hexagonal yods at centres of tetractyses below the top of the 10-tree = 381 + 1 + 1 = 383.

4. Phillips, Stephen M. Article 12: “New Pythagorean aspects of music and their connection to superstrings,” (WEB, PDF), p. 11. 
5. Phillips, Stephen M. Article 16: “The tone intervals of the seven octave species and their correspondence with octonion algebra and superstrings,” (WEB, PDF), p. 12. 
6. Phillips, Stephen M. Article 40 (Parts 1–4): “The unification of all sacred geometries and its implication for particle physics,” Part 1: (WEB, PDF), Part 2: (WEB, PDF), Part 3: (WEB, PDF), Part 4: (WEB, PDF). 
7. Phillips, Stephen M. Article 27: “How the disdyakis triacontahedron embodies the structural parameter 1680 of the E₈×E₈ heterotic superstring,” (WEB, PDF), p. 6. 
8. Phillips, Stephen M. Article 2: “The physical plane and its relation to the UPA/superstring and spacetime,” (WEB, PDF), pp. 10–15. 
9. Phillips, Stephen M. Article 26: “How the seven musical scales relate to the disdyakis triacontahedron,” (WEB, PDF), p. 25. 
10. Phillips, Stephen M. Article 32: “Derivation of the bones & classical acupuncture compositions of the human body and their relationship to the seven musical scales,” (WEB, PDF), pp. 29–31. 
11. Phillips, Stephen M. Article 38: “The geometrization of the seven musical scales and its mathematical implications,” (WEB, PDF), p. 22–26. 

12