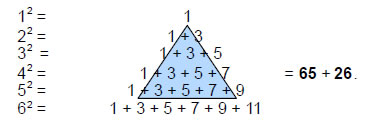ARTICLE 38
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
|
The seven possible types of musical scales contain 14 different types of notes (7 notes and their 7 tonal “complements”). The 91 intervals between these notes are found to consist of 40 Pythagorean intervals (notes belonging to the Pythagorean musical scale) and 51 non-Pythagorean intervals. As a sequence of monotonically increasing tone ratios, they group into 65 intervals up to the 7th note and 26 larger intervals that are complements of some of these intervals. This shows how the Divine Name ADONAI with gematria number value 65 and the Godname YAHWEH with number value 26 prescribe the composition of the 91 intervals between the basic set of 14 notes. The Godname EHYEH with number value 21 prescribes the 21 intervals that are not notes of the seven scales because they are intervals between notes belonging to different scales. EHYEH also prescribes all 91 intervals because 91 is the sum of the 21 odd integers making up the squares of the first 6 integers. There are 25 pairs of notes and their complements. The Godname ELOHIM with number value 50 prescribes these 50 intervals. The Godname ELOHA with number value 36 prescribes the 36 intervals between the eight notes of each scale. The Godname YAH with number 15 prescribes the 15 intervals that have no complements. The Godname YAHWEH ELOHIM with number value 76 prescribes the number of remaining intervals that do have complements. There are 24 pairs of intervals other than 1 and the octave. EHYEH prescribes the 21 pairs that are notes, as well as the 21 types of intervals found in them. The 24 pairs of intervals are symbolized by the 24 pairs of vertices and their mirror images outside the shared root edge of the first (6+6) enfolded polygons of the inner Tree of Life. They are also symbolized by the 24 vertices that are above or below the equator of the disdyakis triacontahedron, its 12 vertices representing the 12 basic notes between the tonic and octave found in the 7 musical scales. The 8 basic intervals and their 8 complements found in the set of 90 intervals below the octave are analogous to the 8 simple roots of E8 and the 8 simple roots of E8' appearing in E8×E8' heterotic superstring theory. There are also 8 triplets of notes with tone ratios in the proportion 1:T:T2, where T (=9/8) is the tone ratio of the Pythagorean tone interval. As four triplets of intervals and four triplets of their complements, they are the counterpart of the four trigrams of the I Ching and their four polar opposites with yang and yin lines interchanged. They are also the counterpart of the 8 unit octonions. The geometrical realisation of the 26 unpaired intervals and the 24 pairs of intervals is a polyhedron with 144 faces and 74 vertices, of which 26 vertices belong to its underlying disdyakis dodecahedron, the remaining 24 diametrically opposite pairs pointing outward from the 24 pairs of faces of this polyhedron. These 24 pairs of intervals spanning the octave constitute the source of the 7 musical scales. They group into 8 sets of 3 intervals and their 3 complements with tone ratios in the proportions 1:T:T2. The 90 edges in one half of the disdyakis triacontahedron represent the 90 rising intervals below the octave. The 90 edges in its other half represent the 90 falling intervals. The 6 edges and their mirror images in its equator represent the six rising intervals of a perfect fifth and the six falling intervals of a perfect fifth. The 168 edges outside the equator and the 168 intervals other than these 12 intervals are both analogous to, if not actual manifestations of, the 168 symmetries of the group PSL(2,7), whose centre, SZ(3,2), is isomorphic to the 3rd roots of 1: 1, r & r2, where r = exp(2πi/3). |
1
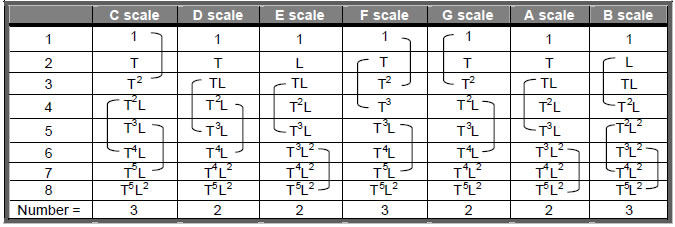
Table 1. Tone ratios of the notes in the seven musical scales.
Musical scale B scale A scale G scale F scale E scale D scale C scale (Tone ratios belonging to the Pythagorean scale are written in black and non-Pythagorean tone ratios are written in red).
The seven species of musical octaves1 comprise 14 different notes (Table 1). In order of increasing tone ratios, they are:
1 256/243 9/8 32/27 81/64 4/3 1024/729 729/512 3/2 128/81 27/16 16/9 243/128 2
They form seven pairs of notes x and their complements y, where xy = 2
1.
1
2
T5L2
2. L
256/243 243/128
T5L
3. T
9/8
16/9
T4L2
4. TL
32/27
27/16
T4L
5. T2 81/64
128/81
T3L2
6. T2L 4/3
3/2
T3L
7. T2L2 1024/729
729/512
T3
(T = 9/8 is the Pythagorean tone interval and L = 256/243 is the Pythagorean leimma). Let X = (x1,x2,x3, …x7) be the set of the first seven notes (xm>xn for m>n) and Y = (y1,y2,y3, ...y7) be the set of their complements (x7<yn<ym for m>n), where xny8-n = 2. There are (14C2 = 91) intervals between the 14 notes. The largest of these is the octave, so that 90 intervals are below it. Their explicit values can be calculated in three steps:
1. Work out the (7C2 = 21) rising intervals Xnm between the notes xn and xm in X (m>n), where Xnm ≡ xm/xn. By definition, xn = X1n;
2. Work out the 21 rising intervals Ynm between the notes yn and ym in Y (m>n), where Ynm ≡ ym/yn. As ym = 2/x8-m and yn = 2/x8-n, Ynm = x8-n/x8-m = X(8-m)(8-n)
3. Work out the (7×7=49) rising intervals Znm between the notes xn and ym, where Znm ≡ ym/xn = 2/x8-mxn. By definition, yn= Z1n, so that the octave y7 is Z17.
Tables 2, 3 & 4 display the magnitudes of the 90 rising intervals below the octave.
Table 2. Intervals Xnm.
n m 1 2 3 4 5 6 7 (Cells highlighted in turquoise are the tone ratios of the first seven notes. Cells for the falling intervals are left blank).
The 21 intervals Xnm consist of 3 Pythagorean notes, 5 Pythagorean intervals, 3 non-Pythagorean notes and 10 non-Pythagorean intervals.
2
Table 3. Intervals Ynm.
(The 7 complements are tabulated in order of decreasing tone ratio in order to demonstrate that the set of 21 intervals Ynm is identical to the set of 21 intervals Xnm).
The 21 intervals Ynm comprise 8 Pythagorean intervals and 13 non-Pythagorean intervals.
Table 4. Intervals Znm.
(The cell with tone ratio 2 is coloured black to indicate that it does not belong to the set of 90 intervals).
The 48 intervals Znm below the octave consist of 3 Pythagorean notes, 20 Pythagorean intervals, 3 non-Pythagorean notes and 22 non-Pythagorean intervals, that is, 23 Pythagorean intervals and 25 non-Pythagorean intervals, regarding notes as intervals.
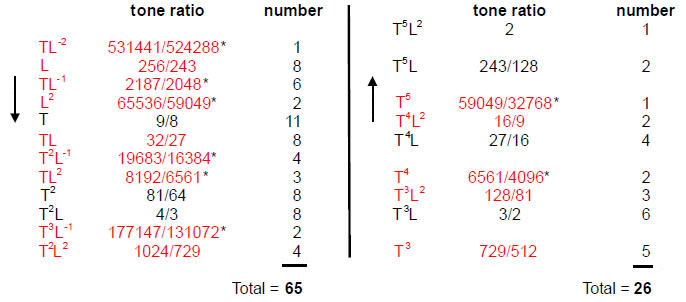
The 91 intervals consist of 7 Pythagorean notes, 6 non-Pythagorean notes, 33 Pythagorean intervals and 45 non-Pythagorean intervals, that is, 40 Pythagorean and 51 non-Pythagorean intervals. In increasing order of size, their tones ratios are:
(The 21 starred intervals are not notes of the seven musical scales). In total, there are 40 Pythagorean intervals and 51 non-Pythagorean intervals. The Godname ELOHIM (Table 5) with number value 50 prescribes the latter because 51 is the 50th integer after 1. There are 65 intervals up to the seventh and last note with tone ratio 1024/729 before the crossover to notes that are complements of the first seven notes. The Godname ADONAI with number value 65 prescribes how many
3
Table 5. Gematria number values of the ten Sephiroth in the four Worlds.
SEPHIRAH
GODNAME
ARCHANGEL
ORDER OF ANGELS
MUNDANE CHAKRA
1 Kether
(Crown)
620EHYEH
(I am)
21Metatron
(Angel of the Presence)
314Chaioth ha Qadesh
(Holy Living Creatures)
833
Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
6362 Chokmah
(Wisdom)
73YAHWEH, YAH
(The Lord)
26, 15Raziel
(Herald of the Deity)
248Auphanim
(Wheels)
187Masloth
(The Sphere of the Zodiac)
1403 Binah
(Understanding)
67ELOHIM
(God in multiplicity)
50
Tzaphkiel
(Contemplation of God)
311
Aralim
(Thrones)
282
Shabathai
Rest.
(Saturn)
317Daath
(Knowledge)
4744 Chesed
(Mercy)
72EL
(God)
31Tzadkiel
(Benevolence of God)
62Chasmalim
(Shining Ones)
428
Tzadekh
Righteousness.
(Jupiter)
1945 Geburah
(Severity)
216
ELOHA
(The Almighty)
36
Samael
(Severity of God)
131
Seraphim
(Fiery Serpents)
630
Madim
Vehement Strength.
(Mars)
956 Tiphareth
(Beauty)
1081
YAHWEH ELOHIM
(God the Creator)
76Michael
(Like unto God)
101
Malachim
(Kings)
140
Shemesh
The Solar Light.
(Sun)
6407 Netzach
(Victory)
148
YAHWEH SABAOTH
(Lord of Hosts)
129
Haniel
(Grace of God)
97Tarshishim or
Elohim
1260
Nogah
Glittering Splendour.
(Venus)
648 Hod
(Glory)
15
ELOHIM SABAOTH
(God of Hosts)
153
Raphael
(Divine Physician)
311
Beni Elohim
(Sons of God)
112
Kokab
The Stellar Light.
(Mercury)
489 Yesod
(Foundation)
80
SHADDAI EL CHAI
(Almighty Living God)
49, 363Gabriel
(Strong Man of God)
246
Cherubim
(The Strong)
272
Levanah
The Lunar Flame.
(Moon)
8710 Malkuth
(Kingdom)
496
ADONAI MELEKH
(The Lord and King)
65, 155Sandalphon
(Manifest Messiah)
280Ashim
(Souls of Fire)
351
Cholem Yesodoth
The Breaker of the
Foundations.
The Elements.
(Earth)
168
(All numbers from this table that are referred to in the article are written in boldface).
4
independent intervals there are between the 14 notes making up the seven musical scales. They are independent in the sense that all other larger intervals complete the octave as their complements and so are determined by them. The Godname YAHWEH with number value 26 prescribes the number of these complementary intervals. The Godname EHYEH with number value 21 prescribes the 21 asterisked intervals (eight types) between notes in different scales.
As 65 is the sum of the first 10 integers after 1:
we see how the Decad, given the title “All Perfect” by the ancient Pythagoreans, defines the number of independent intervals between the 14 different notes in the seven musical scales.
Excluding the octave leaves 25 complements. The 65:25 division of intervals below the octave between the 14 notes is represented in the Lambda Tetractys (Fig. 1). The sum of the four numbers forming its base is 65 and the sum of the six remaining numbers is 25. That this is no coincidence is the fact that the 65 intervals are made up of 27 Pythagorean intervals, 18 that are not notes in the seven scales, 12 non-Pythagorean intervals and eight leimmas of 256/243, all of which are the numbers forming the base of the Lambda Tetractys. Indeed, the central number
6 denotes the number of perfect fifths, the number 4 denotes the number of the note A with tone ratio 27/16, the number 2 is the number of the note B with tone ratio 243/128, the number 1 denotes the largest tone interval 59049/32768 not belonging to the seven scales, the number 3 is the number of intervals 128/81 and the number 9 is the number of intervals 729/512, 6561/4096 and 16/9. In other words, every number in the Lambda Tetractys denotes the number of different subsets of intervals in the set of 90 intervals between the notes of the seven musical scales. This reveals the amazing, archetypal quality of the Lambda Tetractys in quantifying such holistic systems, as well as in defining the tone ratios themselves as ratios of its numbers.
The same 65:26 division as that exhibited by the intervals between the 14 different notes of the seven scales is expressed arithmetically by the fact that 91 is the sum of the squares of the first six integers:
91 is the sum of 21 odd integers, showing how this number is prescribed by the Godname EHYEH with number value 21 (the sum of the first six integers). The sum of the six integers within the central blue triangles is 26, which is the number of intervals with tone ratios that takes them past the crossover between notes and their complements. The sum of the 15 integers on its boundary is 65, which is the number of intervals that are not notes and which are not paired with their complements (see below). 15 is the number value of YAH, the older version of the Godname YAHWEH.
EHYEH determines the 21 intervals that are not notes of the seven scales. This leaves 40 Pythagorean intervals and 30 non-Pythagorean intervals that are notes, that is, 70 intervals. YAHWEH determines the 27 Pythagorean intervals before the crossover into complementary notes because 27 is the 26th integer after 1.
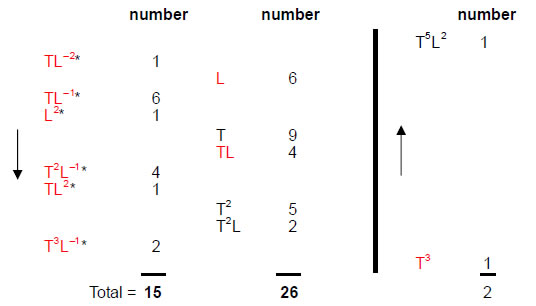
Let us now examine those intervals that do or do not have complements. There are 15 intervals without complements, none of which are found as notes in the seven musical scales. They are of the type TL-2, TL-1, T2L-1 and T3L-1. This means that
5
there are (91–15=76) intervals, some of which are paired as an interval and its complement. This shows how the Godname YAHWEH ELOHIM with number value 76 prescribes these intervals. Six of these are not notes of the scales, leaving 70 intervals that are notes. Some of them, however, cannot be paired with their complements because the number of complements for a given interval is not always equal to the number of intervals of that type.
Tabulated below in order of increasing tone ratio are the number of intervals of each type that are left after the 24 pairs of intervals and their complements are subtracted from the complete set of 91 intervals between the 14 notes of the seven scales:
The Godname YAH with number value 15 prescribes the number of unpaired intervals that are not notes and the full Godname YAHWEH with number value 26 prescribes the number of unpaired notes before the crossover point. There is one note T3 and the octave T5L2 after the crossover point. There are 24 pairs of notes and their complements (see below), so that the set of 76 intervals consists of 26 unpaired notes before the crossover point and 50 other intervals. This reflects the number values 26 and 50 of the words YAHWEH and ELOHIM in the Godname YAHWEH ELOHIM.
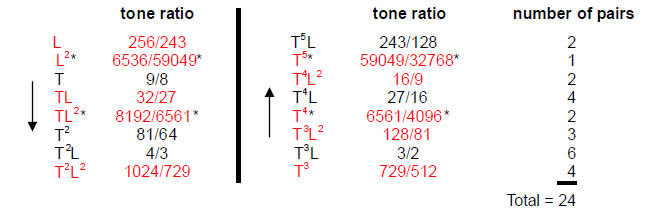
Listed below are those intervals between the tonic and octave and their numbers that do form pairs of intervals and their complements:
There are 48 intervals forming 24 pairs. Including the tonic and octave, there are 25 pairs, i.e., 50 intervals. The Godname ELOHIM with number value 50 prescribes how many of the intervals between notes in the seven scales actually group together as complementary pairs. Including the tonic and octave, there are 25 Pythagorean intervals and 25
6
non-Pythagorean intervals. The 25:25 split exists not only for the intervals and their complements but also for Pythagorean and non-Pythagorean intervals! There are 49 intervals above the tonic that form pairs, showing how EL CHAI, the Godname of Yesod with number value 49, prescribes the spectrum of intervals between the 13 notes above the tonic. There are (49–13=36) intervals that are not notes (i.e., 18 pairs), showing how ELOHA, Godname of Geburah with number value 36, prescribes these intervals. The 50 intervals therefore become 36 intervals. This illustrates how the musical potential defined by ELOHIM, Godname of Binah, becomes restricted by ELOHA, the Godname of the Sephirah below Binah on the Pillar of Severity.
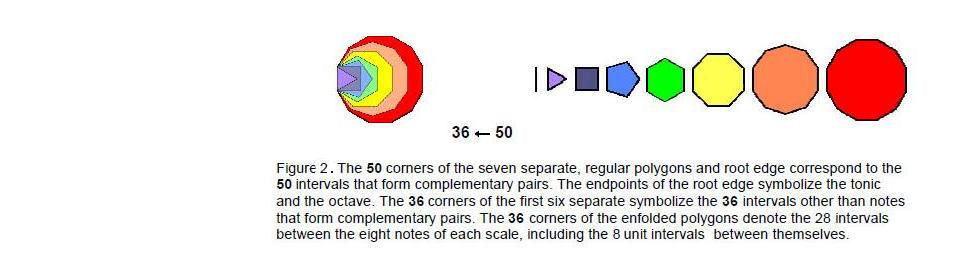
This 50→36 reduction is geometrically represented in the inner form of the Tree of Life (Fig. 2). The seven separate polygons have 48 corners symbolizing the 48 intervals that can form complementary pairs. The two endpoints of the root edge, which formally are corners, symbolize the unit interval and the octave. Together, they constitute 50 corners. The 12 notes in the seven scales other than the octave are symbolized by the 12 corners of the dodecagon. The 36 corners of the first six separate polygons symbolize the intervals forming pairs that are not notes. These extra musical intervals are symbolized by the 36 corners of the seven enfolded polygons.
The intervals in three pairs are not notes of the seven scales, leaving 21 pairs that are such notes. EHYEH prescribes those pairs of intervals and their complements that are notes of the scales. There are (8+8=16) types of intervals, 12 of which are notes of the seven scales and four of which are not. Taking into account the four types of intervals that have no complements, the 14 notes of the seven scales have (16+4+1=21) types of intervals. EHYEH prescribes how many kinds of intervals there are in the 91 intervals between the 14 notes.
There are 16 types of rising intervals below the octave (6 Pythagorean, 10 non-Pythagorean). Including the octave, there are 17 types (7 Pythagorean, 10 non-Pythagorean). Similarly, there are 16 types of falling intervals with tone ratios that are the reciprocal of those of the rising intervals. Including the interval 1, there are (16+1+16=33) rising and falling types of intervals between the 24 pairs of intervals. 33 = 1! + 2! + 3! + 4! and 24 = 1×2×3×4. This demonstrates how the Pythagorean integers 1, 2, 3, 4, which are symbolized by the tetractys and whose ratios define the octave, perfect fifth and perfect fourth, express the number of pairs of intervals and the number of types of intervals in them.
Including the unit interval and octave, the (9+9=18) types of intervals form 25 pairs:
1 2/1 (×1) L 2/L (×2) L2* 2/L2* (×1) T 2/T (×2) TL 2/TL (×4) TL2* 2/TL2* (×2) T2 2/T2 (×3) T2L 2/T2L (×6) T2L2 2/T2L2 (×4) (As before, the tone ratios of intervals written in red are not those of notes in the Pythagorean scale, and asterisked intervals are not notes of the seven musical scales). Figure 3 shows how they constitute a Tree of Life pattern. The first (6+6) enfolded polygons are a subset of the (7+7) enfolded polygons that constitute such a pattern in themselves because they, too, are prescribed by the Godnames of the ten Sephiroth.2
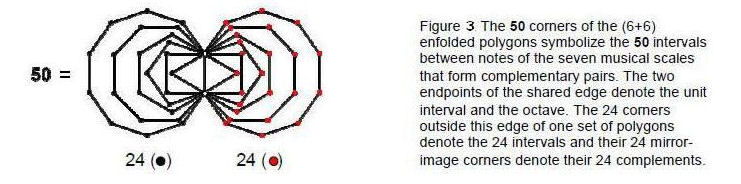
The 50 intervals are symbolized by the 50 corners of the first (6+6) enfolded polygons (Fig. 3). The unit interval and the octave are denoted by the two endpoints of the shared root edge. The 24 intervals and
7
their complements are symbolized by the 24 corners on each side of this edge. The mirror symmetry of the two sets of polygons is the geometrical counterpart of the complementarity between certain pairs of notes. The detailed correspondence between intervals and corners is set out below:
Interval Complement Corner of triangle 1×L2* 1×2/L2* Two corners of square 2×TL2* 2×2/TL2* Three corners of pentagon 3×T2 3×2/T2 Four corners of hexagon 2×L + 2×T 2×1/L + 2×2/T Six corners of octagon 6×T2L 6×2/T2L Eight corners of decagon 4×TL + 4×T2L2 4×1/TL + 4×2/T2L2 The three intervals that are not notes of the seven scales are symbolized by the corners of the triangle and square. This means that the 21 intervals that are notes are naturally symbolised by the 21 corners of the next four polygons.
The eight kinds of intervals between the notes of the seven scales that form pairs correspond to the eight trigrams of the Taoist I Ching:
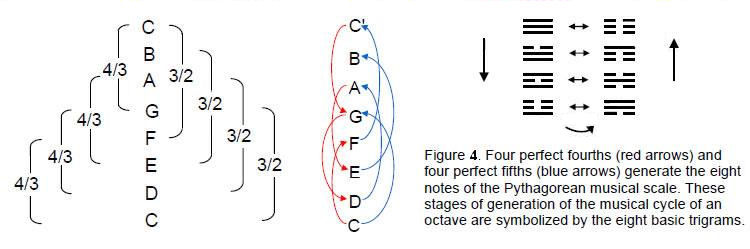
This is another example of the eight-fold way discussed in Article 193 They divide into two sets of four trigrams that express the two Yang/Yin halves of a cycle. A musical octave is such a cycle and its eight notes, symbolised by the eight trigrams, are created by leaps of four perfect fifths and four perfect fourths (Fig. 4). The ancient Greeks regarded the eight-note musical scale as two joined tetrachords, or groups of four notes. The fact that eight-fold cyclical systems divide into two sets of four phases raises the question of whether the eight types of intervals naturally split into two quartets.
We pointed out in Article 32 that the 12 notes between the tonic and octave that create the seven musical scales form two triplets: (T, T2, T3) and (T2L2, T3L2, T4L2), whose tone ratios are in the proportions 1:T:T2, and two triplets (L, TL, T2L) and (T3L, T4L, T5L), whose tone ratios are in the same proportions. There are therefore four triplets with the same proportions of their tone ratios. In each pair of triplets, one triplet contains notes that are the complement of their corresponding notes in the other triplet. These double and triple relationships can be represented by two Stars of David (Fig. 5), one nested inside the other. The three points of one red or blue triangle denote a triplet of notes and the three points of the inverted blue or red triangle denote the ‘antitriplet’ of its complementary notes. The tonic and octave may be thought of as the centre of the star nest. There are two triplets of intervals and two antitriplets of their corresponding complements. Adding the two intervals L2* and TL2* that do not belong
to any scale to the former and their complements to the latter will create two quartets of intervals, so
8
that the eight basic intervals can be divided into two halves, thus upholding the ancient view of the number 8 as “twice 4.”4
According to Tables 2, 3 & 4, L2* = 6536/59049* appears twice either as X57 = 1024/729 ÷81/64 or as Y31 = 128/81÷729/512. In either case, the pair of tone ratios does not appear within the same scale. TL2* = 8192/6561 appears three times either as X37 = 1024/729÷9/8, Y51 = 16/9÷729/512 or as Z53 = 128/81÷81/64. In all three cases, the two tone ratios do not appear in the same scale. This means that the extra two intervals L2* and TL2* and their six complements added to the six intervals and their complements are between two notes in different scales. In other words, they do not appear when music is played in any one scale, only if the available notes are all 14 notes.
The eight basic intervals L, L2*, T, TL, TL2*, T2, T2L & T2L2 and their eight complements have their counterpart in superstring theory as the eight roots of E8 and the eight roots of E8'. Musically speaking, the division of the octave into notes and their complements corresponds to the distinction in the E8×E8' heterotic superstring theory between superstrings of ordinary matter governed by E8 and superstrings of shadow matter governed by E8'. In music, the distinction between notes and their complements is the manifestation in tones of the duality of Yang and Yin. The same can be said for the fundamental difference between ordinary and shadow matter. The musical counterpart of the group distinction between E8 and its exceptional subgroup E6 with six roots is the difference between the eight distinct intervals, of which six are actual notes. It may not be coincidental that the dimension 78 of E6 is the number of intervals between the 13 notes of the seven musical scales above the tonic, as 13C2 = 78.
The sequence of nine basic intervals1:
1, L, L2, T, TL, TL2, T2, T2L, T2L2
can be written
(1, L, L2) T(1, L, L2) T2(1, L, L2)
Successive triplets of intervals have the same proportion 1:L:L2 in the tone ratios of the members of each triplet. We discussed earlier that triplets of notes in the seven scales can be found that have the same proportion of 1:T:T2 of the first three notes C, D & E of the Pythagorean scale (C scale). Let us therefore carry out an exhaustive analysis of triplets of intervals drawn from the complete set of 18 intervals that exhibit proportions of the form 1:X:X2, where X = L, T, TL, T2 or T2L (the only possible values, because the largest interval is T5L2 = 2).
X = L.
1. ×1: (1, L, L2) (T5, T5L, T5L2) 2. ×T: (T, TL, TL2) (T4, T4L, T4L2) 3. ×T2: (T2, T2L, T2L2) (T3, T3L, T3L2) 4. ×T3 : (T3, T3L, T3L2) (T2, T2L, T2L2) 5. ×T4: (T4, T4L, T4L2) (T, TL, TL2) 6. ×T5: (T5, T5L, T5L2) (1, L, L2) As (1) is the same as (6), (5) is identical to (2) and (4) is the same as (3), there are three different triplets: (1), (2) & (3).
X = T.
1. ×1: (1, T, T2) (T3L2, T4L2, T5L2) 2. ×L: (L, TL, T2L) (T3L, T4, T5L) 3. ×L2: (L2, TL2, T2L2) (T3, T4, T5) 4. ×T: (T, T2, T3) (T2L2, T3L2, T4L2) 5. ×TL: (TL, T2L, T3L) (T2L, T3L, T4L) 6. ×TL2: (TL2, T2L2, T3L2) (T2, T3, T4) 7. ×T2: (T2, T3, T4) (TL2, T2L2, T3L2) 8. ×T2L: (T2L, T3L, T4L) (TL, T2L, T3L) 9. ×T2L2 (T2L2, T3L2, T4L2) (T, T2, T3) Multiplying by the remaining intervals just replicates the pairs above because they are the complements of the first eight intervals. As (7) is the same as (6), (8) is the same as (5) and (9) is identical to (4), there are six different pairs of triplets: (1)-(6).
X = TL.
1. ×1: (1, TL, T2L2) (T3, T4L, T5L2) ________________________________
1 The asterisk and red lettering for non-Pythagorean intervals are dropped from now on.
9
2. ×T: (T, T2L, T3L2) (T2, T3L, T4L2) 3. ×T2: (T2, T3L, T4L2) (T, T2L, T3L2) 4. ×T3: (T3, T4L, T5L2) (1, TL, T2L2) As (1) & (4) are the same and as (2) and (3) are the same, there are two different triplets: (1) & (2).
X = T2.
1. ×1: (1, T2, T4) (TL2, T3L2, T5L2) 2. ×L: (L, T2L, T4L (TL, T3L, T5L) 3. ×L2: (L2, T2L2, T4L2) (T, T3, T5) 4. ×T: (T, T3, T5) (L2, T2L2, T4L2) 5. ×TL: (TL, T3L, T5L) (L, T2L, T4L) 6. ×TL2: (TL2, T3L2, T5L2) (1, T2, T4) There are three different triplets: (1), (2) & (3). For X = T2L, there is only the triplet: (T, T3L, T5L2). Hence, this case is of no interest.
There are, therefore, 14 independent triplets and their complements:
1 (1, L, L2) (T5 T5L, T5L2) (1-3: X = L) 2 (T, TL, TL2) (T4, T4L, T4L2) 3 (T2, T2L, T2L2) (T3, T3L, T3L2) 4 (1, T, T2) (T3L2, T4L2, T5L2) (4-9: X = T) 5 (L, TL, T2L) (T3L, T4L, T5L) 6 (L2, TL2, T2L2) (T3, T4, T5) 7 (T, T2, T3) (T2L2, T3L2, T4L2) 8 (TL, T2L, T3L) (T2L, T3L, T4L) 9 (TL2, T2L2, T3L2) (T2, T3, T4) 10 (1, TL, T2L2) (T3, T4L, T5L2) (10-11: X = TL) 11 (T, T2L, T3L2) (T2, T3L, T4L2) 12 (1, T2, T4) (TL2, T3L2, T5L2) (12-14: X = T2) 13 (L, T2L, T4L) (TL, T3L, T5L) 14 (L2, T2L2, T4L2) (T, T3, T5) Seven triplets [(1)-(6) & (10)] have intervals in the first half of the octave (they are all notes in four of them). There are even triplets of intervals [(2), (3) & (5)-(9)] other than 1 with X = L or T. There are also seven such triplets with X = T or T2. Of these, five [(5)-(9)] show the proportions 1:T:T2 and two [(13) & (14)] show the proportions 1:T2:T4. They are shown below:
1 (L, TL, T2L) (T3L, T4L, T5L) (1-5: X = T) 2 (L2, TL2, T2L2) (T3, T4, T5) 3 (T, T2, T3) (T2L2, T3L2, T4L2) 4 (TL, T2L, T3L) (T2L, T3L, T4L) 5 (TL2, T2L2, T3L2) (T2, T3, T4) 6 (L, T2L, T4L) (TL, T3L, T5L) (6-7: X = T2) 7 (L2, T2L2, T4L2) (T, T3, T5) They contain the intervals L2, TL2 and their complements. These are not notes of the seven scales, merely intervals between notes in different scales. There are six triplets [(4), (5), (7), (8), (12) & (13)] with X = T or T2 whose intervals are all notes. There is one triplet (3) with X = L whose intervals are notes. Hence, there are seven triplets all of whose intervals are notes with X = L, T or T2.
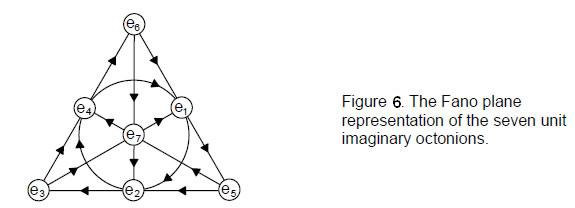
However the seven triplets be defined, they bear a striking correspondence to the seven 3-tuples of octonions, as now explained. The octonions are the numbers of the fourth and last class of division algebras. They are linear combinations of the eight unit octonions ei (i = 0, 1, 2, … 7) that consist of the real unit octonion e0 = 1 and seven unit imaginary octonions ej (j = 1-7) whose multiplication is non-associative and non-commutative:
eiej = -δije0 + Σfijkek (i, j, k = 1, 2,….7)
where fijk is antisymmetric with respect to the indices i, j, k and has values 1, 0, & -1. The seven unit imaginary octonions form seven 3-tuples (ei, ei+1, ei+3) with the cyclic property of multiplication
eiei+1 = ei+3.
Their explicit forms are listed below:
(e1, e2, e4)
10
(e2, e3, e5)
(e3, e4, e6)
(e4, e5, e7)
(e5, e6, e1)
(e6, e7, e2)
(e7, e1, e3)Their multiplication is geometrically represented by the Fano plane (Fig. 6), which is the simplest projective plane. A projective plane of order n consists of (1+n+n2) points and (1+n+n2) lines. The Fano plane is of order n = 2 because it comprises seven points and seven lines. The eight notes of the Pythagorean scale are analogous to the eight unit octonions.
As a note, the tonic can have any pitch, being simply the base with respect to which the tone ratios of the other notes are measured. It corresponds to e0 = 1, the base of the real numbers. The seven rising intervals ni above the tonic correspond to the seven unit imaginary octonions, their falling intervals (their reciprocals 1/ni) corresponding to the conjugates of the imaginary octonions ei* = -ei, so that eiei* = 1 = ni×1/ni. Alternatively, the counterpart of conjugate octonions may be thought of as the complement m of a note n, where nm = 2.
The counterparts of the seven 3-tuples are the seven musical scales. Table 1 shows the tone ratios of their notes. Table 6 shows their composition in terms of the T and L.
Table 6. Intervallic composition of the notes of the seven musical scales.
The 17 triplets that show a 1:T:T2 scaling of their tone ratios are not all different. Including the triplet (1, T, T2), there are eight distinct triplets (four triplets of intervals and four triplets of their complements):
11
This is another musical counterpart of the eight trigrams, the Yang/Yin polarities of the lines and broken lines in each one corresponding to the intervals and their complements. It is also the musical counterpart of the eight unit octonions, with (1, T, T2) being equivalent to the real unit octonion e0 and the seven other triplets being equivalent to the seven imaginary octonions.
Each musical scale is unchanged under interchange of each note and its complement. Similarly, the Fano plane is invariant under interchange of its points and lines and the eight trigrams remain the same set when their Yang and Yin lines are interchanged. The seven scales have 168 rising and falling intervals that are repetitions of the basic set of 12 notes between the tonic and octave. In the 64 hexagrams of the I Ching table, there are 28 pairings of different trigrams with 168 Yang/Yin lines. The Fano plane has 168 symmetries described by SL(3,2), the special linear
group of 3×3 matrices with unit determinant over the field of complex numbers. The trigrams are the expression of the 3×3 matrices and their pairing is the counterpart of this field of order 2. SZ(3,2), the centre of SL(3,2), is the set of scalar matrices with unit determinant and zero trace. It is isomorphic to the third roots of 1. The three roots are 1, exp(2πi/3) and exp(4πi/3). Plotted in the Argand diagram, they are located at the three corners of an equilateral triangle. The cyclic group of order 3 is C3 = (1, r, r2), where the generator r = exp(2πi/3) is the primitive third root of 1. It is the counterpart of the generation of the nine basic types of intervals in the seven scales:
(1+T+T2)(1+L+L2) = 1 + L + L2 + T + TL + TL2 + T2 + T2L + T2L2.
It is known that 1 + X + X2 is the only irreducible polynomial of degree 2 on the finite field of order 2. This plus the fact that the algebra of the octonions can be represented by the Fano plane of order 2, which is the simplest of the projective planes
12
of order n that have (1+n+n2) points and lines, is strong evidence that the mathematical analogy between the octonions and the notes of the seven musical scales is significant. It exists because the Pythagorean mathematics of music and the mathematics of octonions are parallel manifestations of a universal paradigm.
Polyhedral geometrization of the seven musical scales
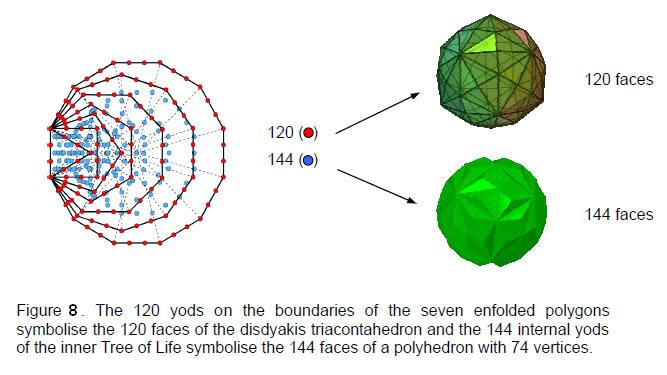
It was found earlier that the maximum number of intervals between the 14 basic notes of the seven scales that have complements is 24, leaving 26 unpaired intervals before the crossover into the complements of these intervals. There are therefore 74 such intervals. Table 5 in Article 265 indicates that there are no Archimedean or Catalan solids with 74 vertices. However, the disdyakis dodecahedron has 48 faces and 26 vertices. If a tetrahedron is attached to each face, the resulting polyhedron has (3×48=144) faces and (48+26=74) vertices (Fig. 7). This polyhedron was discussed in Article 24 as being the ‘yang’ counterpart of the ‘yin’ disdyakis triacontahedron, i.e., they constitute a dualistic whole. Remarkable evidence of this is that the 264 faces of both polyhedra are symbolised by the 264 yods of the inner Tree of Life, the 120 yods on their boundaries symbolising the 120 faces of the disdyakis triacontahedron and the 144 yods inside them denoting the 144 faces of the polyhedron (Fig. 8). The 48 peaks of the tetrahedra correspond to the 24 pairs of complementary intervals and the 26 original vertices correspond to musical intervals that are left over, so to speak, unable to form such pairs, and therefore not actively participating in the embodiment of the seven musical scales in the disdyakis triacontahedron. These play a dynamic, generative role because creation is a cyclic interplay of Yang and Yin represented by intervals and their complements making up the octave cycle and no more than 24 tonal intervals (yang) have their complementary opposites (yin). Indeed, we are countenancing here the pattern-determining character of the number 24, as explained in other contexts in Article 37.6 The number 48 is the number value of Kokab, the Mundane Chakra of Hod (Table 1), and its 24:24 division is characteristic of holistic systems that embody the divine paradigm, as the first (6+6) enfolded polygons of the inner Tree shown in Fig. 3 illustrate.The polyhedron with 144 faces and 74 vertices spatially represents the musical potential in terms of intervals between the basic set of 14 notes that make up the seven scales, whilst the disdyakis triacontahedron represents their organisation into the patterns recognisable as the seven musical scales — the very basis of Western music itself. Its (90+90) edges are the geometrical counterpart of the 90 rising and 90 falling intervals between these notes, i.e., the mirror symmetry in the distribution in space of their edges is the counterpart of the distinction between a rising interval and a falling interval. The 12 edges (six edges & their six mirror images) along the equator of the disdyakis triacontahedron when its ‘north’ and ‘south’ poles are diametrically opposite A vertices denote the six rising and six falling perfect fifths found in the 24 intervals and their complements (the only type of interval to have six copies — see the list on page 7). These 6:84 divisions in each set of 90 intervals and in the edges of the disdyakis triacontahedron are, respectively, the musical and geometrical manifestation of the mathematical archetype represented by Plato’s Lambda Tetractys:
Its ten integers add up to 90, that is, the nine integers surrounding the central integer 6 add up to 84. The 168 remaining intervals that are not perfect 5ths (84 rising and 84 falling) correspond to the 84 edges above the equator and the 84 edges below the equator. The 24 vertices above the equator symbolize the maximal set of 24 intervals, which are matched by their complementary intervals denoted by the 24 vertices below the equator. The two remaining vertices (the poles of the disdyakis triacontahedron) denote the tonic and the octave — the beginning and the end of the musical scale.
Figure 8 shows how this information is embodied in the dodecagon — the last of the regular polygons enfolded in the inner Tree of Life. When its sectors are divided into three tetractyses, there are 180 yods surrounding its centre. They symbolize the 180 edges of the disdyakis triacontahedron — the polyhedral realisation of the inner Tree of Life. They also denote the 180 rising and falling intervals below the 14 notes of the seven musical scales. The 12 vertices of the 36 tetractyses making up the dodecagon correspond to the 12 edges in the equator of the disdyakis triacontahedron and, in the musical context of the intervals, the six rising perfect fifths (3/2) and the six falling perfect fifths (2/3). The 84 remaining yods in six sectors are the counterpart of the 84 edges above the equator and the 84 rising intervals. The 84 yods in the other six sectors are the counterpart of the 84 edges below the equator and the 84 falling intervals. The central yod signifies the tonic as the starting note. Its counterpart in the disdyakis
13
triacontahedron is the imaginary, internal line joining two diametrically opposite A vertices — the axis of the polyhedron.
Of the (24+24) intervals, there are 21 notes and 21 complements with tone ratios of notes in the seven scales. Interestingly, Table 1 indicates that there are actually just 21 notes with these tone ratios! This demonstrates how the Godname EHYEH with number value 21 prescribes the composition of the 91 intervals between the 14 different notes of the seven scales. The three remaining intervals (one L2* and two TL2*) are not notes. This 3:21 differentiation was found in Article 217 in the context of the 24 lines and broken lines
making up the eight trigrams. The positive and negatives lines of each trigram denote the positive and negative directions with respect to a rectangular coordinate system of the three perpendicular faces of a cube whose intersection is one of its eight corners. If such cubes are stacked together, any one corner of a cube coincides with the corners of seven other cubes (three on the same level and four either above or below it). This means that a cubic lattice point is defined by the intersections of three faces belonging to eight cubes, three belonging to the cube itself and 21 belonging to the seven cubes that surround it.
The same 3:21 division appears in the Klein Configuration.8 This is the hyperbolic mapping of the 168 automorphisms of the equation known to mathematicians as the “Klein quartic”:
x3y + y3z + z3x = 0.
These symmetries of its Riemann surface can be mapped onto the hyperbolic surface of a 3-torus in a number of different ways. Figure 9 shows the {7,3) tiling that requires 24 heptagons divided into 168 coloured triangles. It also has 168 anti-automorphisms represented by the 168 grey triangles of 24 other heptagons. These two sets of 24 heptagons are the counterpart of the 24 intervals and their 24 complements. The three intervals and their complements that are not notes of the seven scales correspond, respectively, to the three cyan triangles in Figure 9 at the corners of a half-sector and to the three grey triangles at the corresponding corners of the other half-sector. Notice that the one L2* and the two TL2* intervals in the set of 24 match, respectively, the innermost triangle and the two outermost triangles in a half-sector. They correspond in the 3×3×3 array of cubes displaying an isomorphism with the Klein configuration to the three faces of the central cube intersecting at one corner.9 The 168 automorphisms of the Klein quartic correspond to the 168 rising and falling intervals other than the six perfect fifths and to the 168 edges above and below the equator of the disdyakis triacontahedron,10 its six edges and their inverted images corresponding, respectively, to the six rising perfect fifths and to the six falling perfect fifths in the 90 intervals below the octave between the 14 notes of the seven scales. Both are the manifestation of the projective, special linear group PSL(2,7), which is the quotient group SL(2,7)/{1,-1}, where 1 is the identity matrix, and SL(2,7) consists of all 2×2 matrices with unit determinant over F7, the finite field with 7 elements. These elements can be the seven types of intervals between notes of the seven musical scales and the seven unit imaginary octonions ei, whose algebra is represented by the Fano plane with the symmetry group SL(3,2) that is isomorphic to PSL(2,7). Their seven conjugates ei* = -ei, where eiei* = 1, correspond to the complements yi of the seven notes xi, where xiyi = 2, whilst their seven 3-tuplets (ei, ei+1, ei+3) and the seven 3-tuplets of their conjugates (ei*, ei+1*, ei+3*) correspond, respectively, to the seven triplets of intervals and to the seven triplets of their complements that display the same relative proportions 1:T:T2. of their tone ratios.
Whether the 168 rising and falling intervals are actual elements of PSL(2,7) is irrelevant except to one who cannot see the larger picture. Anyone who demands a formal proof that they form this group before he takes the analogy seriously is missing the crucial point. Such proof is necessary only if one makes the stronger claim that the intervals are such elements. However, judging the similarity to be significant evidence of a universal principle because it is too implausible to be due to chance does not require this
14
stronger version to be made. What is sufficient is to demonstrate that:
1. the mathematical properties of the two sets of seven basic intervals found in the seven musical scales are at least analogous to the properties of PSL(2,7) in too many ways for this to be coincidental;
2. these properties can be represented by the polygonal and polyhedral forms of the outer and inner Trees of Life in too much detail and in too natural a way either for the matching to be contrived, i.e., for it to indicate anything other than that PSL(2,7) and the musical intervals between the notes in the seven scales embody the same, essential Tree of Life pattern. This is what has been done here.
If such matching cannot plausibly be attributed to coincidence because it is too detailed, two systems can be mathematically analogous only because they are both holistic in nature and therefore manifest in their own way — physically or conceptually — the same, universal paradigm. The mathematical patterns in a system and in some symmetry group need only be similar in appearance. The former does not necessarily have to amount formally to a group symmetry that is isomorphic to the latter in order to constitute evidence of such a paradigm. The fact that such extensive analogy exists between topics as diverse as octonions, the eight simple roots of E8, musical scales and acupuncture meridians, as demonstrated in this and previous articles, is not an illusion due to some contrived selection of features that match and the ignoring of those that do not. The remarkable, natural appearance of at least eight Godname numbers to prescribe the properties of the 90 intervals totally discredits such a suggestion and confirms the status of the seven musical scales as a holistic system that embodies the Tree of Life pattern. It indicates that a universal principle connects all these systems as different facets of a pervading Unity hidden within diversity. Its polyhedral realisation is the disdyakis triacontahedron.
References
1 Phillips, Stephen M. Article 14: "Why the Seven Greek Musical Modes are Sacred," (WEB, PDF).2 Phillips, Stephen M. Article 4: "The Godnames Prescribe the Inner Tree of Life," (WEB, PDF), pp. 4–5.
3 Phillips, Stephen M. Article 19: "I Ching and the Eight-fold Way," (WEB, PDF).
4 Ibid, p. 6.
5 Phillips, Stephen M. Article 26: "How the Seven Musical Scales Relate to the Disdyakis Triacontahedron," (WEB, PDF), Table 5, p. 13.
6 Phillips, Stephen M. Article 37: "The Seven Octaves of the Seven Musical Scales are a Tree of Life Pattern Mirrored in the Disdyakis Triacontahedron," (WEB, PDF).
7 Phillips, Stephen M. Article 21: "Isomorphism between the I Ching Table, the 3×3×3 Array of Cubes and the Klein Configuration," (WEB, PDF), pp. 2–4.
8 Phillips, Stephen M. Article 15: "The Mathematical Connection Between Superstrings and Their Micro-psi Description: a Pointer Towards M-theory," (WEB, PDF), pp. 24–28; also ref. 3, pp. 29–30.
9 Ref. 6, p. 8.
10 Ibid, Fig. 35, p. 34.
15