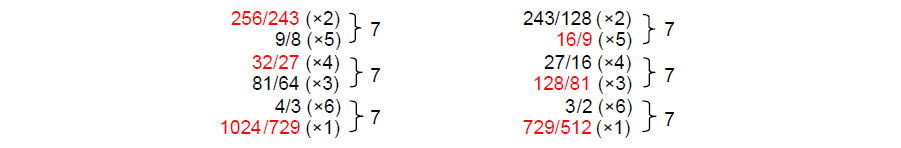ARTICLE 46

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://smphillips.mysite.com

 

 

Abstract

1

Introduction

Ever since Charles Darwin published his Origin of Species, debate has raged in the West between scientists, humanists and Christians about whether humans are the end result of either a busy week of terra-forming by God, an evolutionary process guided by God (so-called “intelligent evolution”) or merely an accidental by-product of random mutations and geological events that favoured the survival only of those who were most fitted to the environment (Darwinian evolution). All the arguments of each camp remain inconclusive to its opponents because, on the one hand, scientists claim that they can explain in conventional terms what some Christian fundamentalists regard as evidence of God designing the morphology of living things, whilst, on the other hand, they dismiss the criticism that there is no evidence for inter-species evolution by arguing that the current gaps in such evidence will be eventually filled. Can this impasse be breached by presenting a new kind of evidence whose existence can only be understood if some universal design does, indeed, permeate biological matter at the molecular level — one whose origin has to be transcendental because it is found in the sacred geometries of major religions of the world? This article will present such evidence that human beings are “made in the Image of God.”

Section 1 will discuss the Tree of Life, the representation of the divine prototype that is the basis of the Jewish mystical tradition called ‘Kabbalah.’ Section 2 analyses aspects of the table of 64 hexagrams whose commentaries form the I Ching (“Book of Changes”), the system of divination that originated in the Taoist religion of ancient China. Section 3 will analyse the composition of intervals between the notes of the seven musical scales and compare them with the structure of this table. The pattern that emerges from these three holistic systems will be compared in Section 4 with the Tantric Sri Yantra. Section 5 will explore its polyhedral counterpart. An example taken from pure mathematics that embodies this universal pattern will be discussed in Section 6. Finally, having established conclusively that a remarkable isomorphism exists between these sacred geometries, it will be shown in Section 7 to extend also to the pattern of base triplets in the DNA molecule that encode the amino acids. So detailed is the correlation between these seven systems that it cannot, plausibly, be explained as the result of chance. To contend that it can amounts to replacing miraculous correspondence with an equally miraculous set of coincidences merely in order to avoid facing implications that contradict the presuppositions of scientific materialism. Only one explanation then remains for why the scientific description of the DNA molecule should, mathematically speaking, conform to the sacred geometries of various religions: the molecule of life embodies the very mathematical nature of God that these geometries are supposed to represent.

1. The 64×3 pattern in the inner Tree of Life

At the heart of Kabbalah is the Tree of Life (Fig. 1). It depicts the divine prototype of Adam Kadmon, or “Heavenly Man.” The ten Divine Qualities, or Sephiroth (sing: Sephirah) are: Kether, Chokmah, Binah, Chesed, Geburah, Tiphareth, Netzach, Hod, Yesod and Malkuth. They are depicted as spheres located at the corners of 16 triangles whose 22 edges are called “Paths.” Midway between Binah and Chesed is Daath (“knowledge”). It is not a Sephirah. It denotes the gulf between the subjective and objective levels of the Tree of Life. The ten Sephiroth are arranged in three vertical columns called the Pillar of Mercy, the Pillar of Equilibrium & the Pillar of Severity (or Judgement). They express active, reactive and homeostatic aspects of the Sephiroth. The uppermost three Sephiroth (Kether, Chokmah & Binah) are called the ‘Supernal Triad.’ They signify the transcendent, triple Godhead, the subjective aspect of God. The seven other Sephiroth are the seven ‘Sephiroth of Construction.’ They signify objective aspects of God. The uppermost nine Sephiroth are related as three triads. This will prove highly significant when the Tree of Life and its counterparts in the sacred geometries of eastern religions are compared with the DNA molecule.

Each Sephirah has four levels or stages of manifestation: Atziluth (Archetypal World), Beriah (World of Creation), Yetzirah (World of Formation) & Assiyah (World of Action). Their respective aspects are the Godnames, Archangels, Order of Angels and Mundane Chakras. The lattermost are the astrological, planetary associations with the Sephiroth. For example, Cholem Yesodoth (symbolized by the planet Earth) is the Mundane Chakra of Malkuth, the outer, material form of the Tree of Life, whatever its realization. Through the practice of gematria, wherein the 22 letters of the Hebrew alphabet are assigned the numbers 1, 2, 3 …10, 20, 30, …100, 200, 300 & 400, with the numbers 500, 600, 700, 800 & 900 assigned to the five final letters, every Hebrew name of the Sephiroth, their Godnames, etc has a number value that is the sum of its letter values (Table 1). For example, the

 

 

 

 

 

2

Table 1. Gematria number values of the ten Sephiroth in the four Worlds.

	SEPHIRAH	GODNAME	ARCHANGEL	ORDER OF ANGELS	MUNDANE CHAKRA
1	Kether (Crown)                  620	EHYEH (I am)                  21	Metatron (Angel of the Presence)                  314	Chaioth ha Qadesh (Holy Living Creatures)                  833	Rashith ha Gilgalim First Swirlings. (Primum Mobile)                  636
2	Chokmah (Wisdom)                  73	YAHWEH, YAH (The Lord)                  26, 15	Raziel (Herald of the Deity)                  248	Auphanim (Wheels)                  187	Masloth (The Sphere of the Zodiac)                  140
3	Binah (Understanding)                  67	ELOHIM (God in multiplicity)                  50	Tzaphkiel (Contemplation of God)                  311	Aralim (Thrones)                  282	Shabathai Rest. (Saturn)                  317
	Daath (Knowledge)                  474
4	Chesed (Mercy)                  72	EL (God)                  31	Tzadkiel (Benevolence of God)                  62	Chasmalim (Shining Ones)                  428	Tzadekh Righteousness. (Jupiter)                  194
5	Geburah (Severity)                  216	ELOHA (The Almighty)                  36	Samael (Severity of God)                  131	Seraphim (Fiery Serpents)                  630	Madim Vehement Strength. (Mars)                  95
6	Tiphareth (Beauty)                  1081	YAHWEH ELOHIM (God the Creator)                  76	Michael (Like unto God)                  101	Malachim (Kings)                  140	Shemesh The Solar Light. (Sun)                  640
7	Netzach (Victory)                  148	YAHWEH SABAOTH (Lord of Hosts)                  129	Haniel (Grace of God)                  97	Tarshishim or Elohim                  1260	Nogah Glittering Splendour. (Venus)                  64
8	Hod (Glory)                  15	ELOHIM SABAOTH (God of Hosts)                  153	Raphael (Divine Physician)                  311	Beni Elohim (Sons of God)                  112	Kokab The Stellar Light. (Mercury)                  48
9	Yesod (Foundation)                  80	SHADDAI EL CHAI (Almighty Living God)                  49, 363	Gabriel (Strong Man of God)                  246	Cherubim (The Strong)                  272	Levanah The Lunar Flame. (Moon)                  87
10	Malkuth (Kingdom)                  496	ADONAI MELEKH (The Lord and King)                  65, 155	Sandalphon (Manifest Messiah)                  280	Ashim (Souls of Fire)                  351	Cholem Yesodoth The Breaker of the Foundations. The Elements. (Earth)                  168

 

The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation, traditionally symbolised by celestial bodies). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving to a word a number value that is the sum of the numbers of its letters.

(All numbers from this table that are referred to in the article are written in boldface).

3

gematria number value of Malkuth is 496,¹ and the number value of its Mundane Chakra is 168, two numbers which have been proven in previous articles to be, respectively, dynamical and structural parameters of the E₈×E₈ heterotic superstring, one of the five types of superstrings.

If the 16 triangles in the Tree of Life were separated, they would have 48 corners and 48 sides, i.e., 112 geometrical elements in all. Therefore, (48–22=26) edges and (48–10=38) corners, i.e., 64 geometrical elements, disappear when the triangles join together to form the Tree of Life  with 48 elements. According  to Table 1, 26  is the number value of YAHWEH, the Godname of Chokmah, which heads the Pillar of Mercy, 64 is the number value of Nogah, the Mundane Chakra of Netzach below Chokmah on this Pillar, 48 is the number value of Kokab, Mundane Chakra of Hod

and 112 is the number value of Beni Elohim, the Order of Angels of this Sephirah (N.B. All Godname numbers will be written in bold format).

Many books on Kabbalah depict the Tree of Life as spanning four similar circles that overlap, circumference to centre (Fig. 2a). As the Tree of Life is three-dimensional, these circles are actually the cross-sections of four similar spheres in the plane containing its side pillars. Consider two identical circles (shown in Fig. 2a by the dashed lines) whose centres are located at Chesed and Geburah — the points of intersection of the second and third circles. Then consider the ends of the horizontal and vertical diameters of these circles, as well as their centres and points of intersection (denoted in Fig. 2a by red dots). Amazingly, the straight lines joining pairs of dots intersect at the 70 corners of two similar sets of seven enfolded, regular polygons (Fig. 2b): the triangle, square, pentagon, hexagon, octagon, decagon & dodecagon. Unknown to Kabbalists, this geometrical object is the ‘inner form’ of the Tree of Life (Fig. 3). It is two-dimensional, whereas the outer form is three-dimensional. Figure 3 depicts the projection of the latter onto the plane containing its inner, polygonal form. Six Sephiroth coincide with the corners of polygons: Chokmah, Binah, Chesed, Geburah, Netzach & Hod. Only the projections of Tiphareth and Daath onto the plane containing the polygons coincide with positions of corners. The single edge shared by all the polygons and having these two projected points as its endpoints will be called the ‘root edge.’

Many previous articles have shown how scientific information is embodied in the inner form of the Tree of Life. It constitutes a ‘whole’ that is prescribed by the Godnames in the sense that its properties are mathematically determined by their gematria number values.² For example, the seven enfolded polygons have 36 corners. 36 is the number value of ELOHA, the Godname of Geburah (see Table 1). Certain subsets of this set are also prescribed by the Godnames. They constitute wholes in themselves that are characterized by the same set of parameters as that which describes all (7+7) enfolded polygons. The largest of these subsets is the two sets of the first six enfolded polygons. As the fourth polygon, the hexagon is the halfway point in the generation of each set of seven polygons from the circles. We shall find later that its counterparts in other sacred geometries play the same role of dividing the whole into two halves, one of which is the mirror image or the inverse of the other.

As the simplest polygon, the triangle is the basic template for the construction of sacred geometry. In the case of the inner Tree of Life, this is performed by dividing its polygons into their sectors. The resulting

 

4

polygons are called ‘Type A.’ A sector may be further divided into three sectors. Such polygons are called ‘Type B.’ Division of sectors may of course be continued indefinitely. For the present purpose of establishing certain patterns shared by sacred geometries, it will be sufficient to consider only the two simplest types.

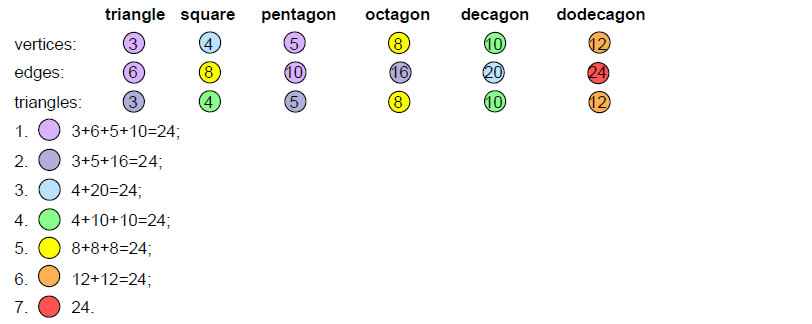
Figure 4 shows the seven separate Type A and Type B regular polygons. Listed below are formulae for the geometrical composition of a polygon with n corners (‘+1’ denotes its centre).

Formulae

	Type A polygon	Type B polygon
Number of vertices =	n+1	2n+1
Number of edges =	2n	5n
Number of triangles =	n	3n
Number of geometrical elements =	4n+1	10n+1
Number of vertices+edges =	3n+1	7n+1
Number of vertices+triangles =	2n+1	5n+1
Number of edges+triangles =	3n	8n

Table 2 shows the numbers of vertices, edges & triangles in the seven Type A or Type B polygons.

Table 2. Geometrical composition of the seven regular polygons of the inner Tree of Life.

	triangle+square +pentagon		hexagon+octagon +decagon		Subtotal		dodecagon		Total
	Type A	Type B	Type A	Type B	Type A	Type B	Type A	Type B	Type A	Type B
vertices	12+3	24+3	24+3	48+3	36+6	72+6	12+1	24+1	48+7	96+7
edges	24	60	48	120	72	180	24	60	96	240
triangles	12	36	24	72	36	108	12	36	48	144
Total	48+3	120+3	96+3	240+3	144+6	360+6	48	120+1	192+7	480+7
vertices+edges	36+3	84+3	72+3	168+3	108+6	252+6	36	84+1	144+7	336+7
vertices+triangles	24+3	60+3	48+3	120+3	72+6	180+6	24	60+1	96+7	240+7
edges+triangles	36	96	72	192	108	288	36	96	144	384

Comments

Type A polygons

The seven separate polygons have 192 vertices, edges & triangles surrounding their seven centres. Hence, the 14 polygons have 384 geometrical elements surrounding their 14 centres. They comprise (24+24) elements in the pair of hexagons and (168+168) elements in the 12 remaining polygons. The numbers of elements that surround the centres of the latter polygons in each set are:

 

5

	triangle	square	pentagon	octagon	decagon	dodecagon	Total
Number of vertices =	3	4	5	8	10	12	42
Number of edges =	6	8	10	16	20	24	84
Number of triangles =	3	4	5	8	10	12	42
Total =	12	16	20	32	40	48	168

The 168 elements in each set of polygons other than the hexagon can be sorted into the following groups:

1. 168 = 84 + 84.
   84 vertices & triangles and 84 edges;
2. 168 = 56 + 56 + 56.
   Number of geometrical elements in square & decagon: 16 + 40 = 56;
   Number of vertices & triangles in triangle, pentagon, octagon & dodecagon = (3+5+8+12) + (3+5+8+12) = 28 + 28 = 56;
   Number of edges in triangle, pentagon, octagon & dodecagon = 6 + 10 + 16 + 24 = 56;
3. 168 = 7×24.
   The 168 geometrical elements can be grouped into seven sets of 24 elements (colours denote sets):

The counterparts of these three types of factorisations in the I Ching table, the Sri Yantra and the disdyakis triacontahedron will be discussed in later sections. Their significance vis-à-vis the Klein Quartic and the mapping of its 168 automorphisms on the 3-torus will be discussed in Section 6.

The 24 geometrical elements surrounding the centre of the Type A hexagon consist of three consecutive vertices, three edges, three internal edges, three triangles and their diametrically opposite counterparts. In other words, they comprise four triplets of elements and their diametric opposites. The seven separate polygons therefore consist of eight triplets of elements and three sets of 56 elements. The latter can be regrouped as 56 triplets of elements, one taken from the square & decagon, one (vertex or triangle) from the triangle, pentagon, octagon & dodecagon and one (edge) from this set. This means that the geometrical composition of the inner Tree of Life divides naturally into (8+56=64) triplets of geometrical elements. The number 64 is the gematria number value of Nogah, the Mundane Chakra of Netzach. It characterizes the DNA molecule

in a way that will be discussed in Section 7.

6

---

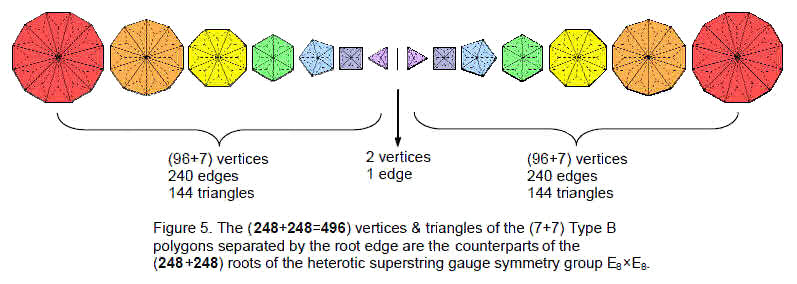
Type B polygons

The seven separate polygons comprise 240 vertices & triangles surrounding their seven centres. Including the root edge separating the two sets of seven separate polygons, the ends of which may be formally counted as vertices, there are (247+2+247=496) vertices & triangles (Fig. 5). 248 vertices & triangles are associated with each set. They comprise an endpoint of the root edge, seven centres and 240 vertices & triangles. This is the geometrical counterpart of the eight simple roots and the 240 roots of the superstring gauge symmetry group E₈. The inner form of the Tree of Life, when viewed as 14 separate regular polygons divided by their root edge, has (248+248=496) vertices & triangles that are the counterparts of the (248+248) roots of E₈×E₈. That this is no coincidence is demonstrated by the fact that the first six polygons have 72 vertices surrounding their six centres, leaving 168 vertices & triangles. This compares with the six simple roots and 72 roots of E₆, an exceptional subgroup of E₈, and the 168 roots of E₈ that are not roots of E₆. As bits of information defining the geometry of the inner Tree of Life, the 248 vertices and triangles are the counterparts of the 248 roots of E₈. As was shown in Article 4,³ the Godnames assigned to the ten Sephiroth of the Tree of Life prescribe both the inner Tree of Life and its largest subset of polygons — the first six polygons and the first (6+6) polygons. For example, YAHWEH with gematria number value 26 and ELOHIM with number value 50 prescribe this subset because the first six enfolded polygons have 26 corners and the first (6+6) enfolded polygons have 50 corners, whilst ELOHA with number value 36 prescribes the six separate polygons because they have 36 corners.

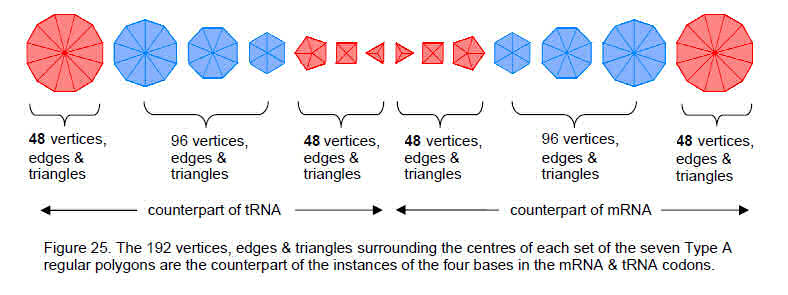
The seven separate Type B polygons have 480 geometrical elements surrounding their centres that are made up of 240 vertices & triangles and 240 edges. 240 geometrical elements surround the centres of the hexagon, octagon & decagon; similarly, 240 geometrical elements surround the centres of the triangle, square, pentagon & dodecagon. The counterparts of this 240:240 division in the Platonic solids, thought by the ancient Greeks to be the shapes of the particles of Fire, Air, Earth & Water, are the 240 hexagonal yods in the 18 faces of the tetrahedron, octahedron & cube and the 240 hexagonal yods in the 20 faces of the icosahedron when they are constructed from tetractyses.⁴ Their 38 faces comprise 120 triangles with 248 vertices & edges,⁵ where

120 = 2² + 4² + 6² + 8².

They are the counterparts of the 248 vertices & triangles associated with the seven separate Type B polygons. This is how the first four Platonic solids embody the dimension 248 of the symmetry group E₈.  

Surrounding the centres of the seven polygons are 336 vertices & edges. They comprise 168 vertices & edges in the triangle, square, pentagon & dodecagon (let us call this set ‘S’) and 168 vertices & edges in the hexagon, octagon & decagon (let us call this set ‘S'’). Notice that S' determines the division of both 480 into two 240s and 336 into two 168s. According to Table 1, S' determines also the division of the 384 edges & triangles in the seven polygons into two equal groups — the 192 edges & triangles in S and the 192 edges & triangles in S'. In fact, this equal division is true for any combination of geometrical elements because the hexagon, octagon & decagon have 24 corners — the same as the number of corners of the triangle, square, pentagon & dodecagon — so that the formulae listed above for each combination imply the same number of elements. The 168:168 division manifests in the ten closed curves of the E₈×E₈ heterotic superstring as the 168 circularly polarized oscillations in a half-revolution of each curve. It appears in the Sri Yantra as the 168 yods on the sides of the 21 triangles in each half when they become tetractyses. It manifests in the disdyakis triacontahedron as the 168 hexagonal yods on its 84 edges on each side of its central plane. The 24:24 division of corners displayed by these two sets of polygons is characteristic of holistic systems.⁶ It reappears in the first (6+6) enfolded polygons as the 24 corners associated with each set of six polygons. It appears in a single polygon as the 24 edges and 24 vertices & triangles in the Type A dodecagon, which embodies holistic properties analogous to all seven polygons. Its analogue in the seven separate Type B polygons are the 24 sides of the triangle, square, pentagon & dodecagon and the 24 sides of the hexagon, octagon & decagon (note: sides, not corners, because they belong to the set of 192 edges & triangles in each set).

The edge/triangle composition of S and S' is shown below (‘+n’ denotes the n sides of a polygon):

Each set has 96 internal edges and 72 triangles, i.e., 168 edges & triangles. The triangle and pentagon

7

---

have 32 internal edges and 24 triangles; the square and dodecagon have 64 internal edges and 48 triangles, that is, twice as many. Similarly, the octagon has 32 edges and 24 triangles and the hexagon and decagon have 64 internal edges and 48 triangles, that is, twice as many. For S and S', the number 168 has the factorisation 7×24, where ‘7’ is the number of internal edges & triangles per sector of a polygon and ‘24’ is the number of sectors in S or S'. Let us label the 32 internal edges & 24 triangles in the triangle & pentagon as A, the 32 internal edges & 24 triangles in half the square & dodecagon as B, the 32 internal edges & 24 triangles in their other half as C, the 32 internal edges & 24 triangles in the octagon as A', a similar set in half the hexagon & decagon as B' and a similar set in their other half as C'. Then S = {A,B,C,24} and S' = {A',B',C',24}, where A, B, C, etc has 56 edges & triangles and ‘24’ denotes the 24 sides of the polygons in S & S'. Each number 168 therefore has the factorisation 56×3. It also has the factorisation 84×2, for the dodecagon has 84 edges & triangles and the triangle, square & pentagon have 84 edges & triangles, whilst the two halves of the polygons in S' each has 84 edges & triangles.

The 24 sides of polygons belonging to S comprise the three sides of the triangle, four sets of three consecutive sides of the dodecagon and three sets of three sides of the square and pentagon, that is, eight triplets of edges. The 24 sides of polygons belonging to S' comprise two sets of three consecutive sides of the hexagon and six sets of three sides of the octagon and decagon, that is, eight triplets of edges. Therefore, S and S' each consist of 64 triplets of edges & triangles, eight of them being the sides of their polygons. Remarkably, the same 64×3 factorisation is

displayed in the seven Type A polygons as in the seven Type B polygons. The number 384 characterizing holistic systems manifests in both sets of

8

---

polygons because each is a whole, which means that they embody the same characteristics of the Tree of Life by manifesting in their own way the same parameters, such as 480, 384, 336 & 168. For example, the 14 Type A polygons have 384 geometrical elements, whilst the seven Type B polygons have 384 edges & triangles. As previous articles have proven, all holistic systems exhibit the same patterns defined by the same set of parameters. This amazing property enables physical objects like the superstring and the DNA molecule to be recognized as such systems. This was demonstrated in earlier articles for the former. It will be proven for the latter in Section 8.

2. The 64×3 pattern in the I Ching table

The ancient Chinese oracular system is known in the West as I Ching (易經), or ‘Book of Changes.’ Pronounced “Ee Jing”, I Ching is about 5,000 years old, making it one of the oldest available sources of spiritual wisdom. It will not be necessary to explain how it is used to provide advice about the future. According to Taoist philosophy, yang and yin, respectively, the positive, or active, and negative, or reactive, phases of nature’s great cycles, emerged from Tai Yi, the “Great Unity,” symbolized by a circle. As opposite states represented by the positive (+) and negative (–) signs, they can be paired in four ways: + +, – +, + – & – –. (Fig. 6). Adding a plus or minus sign at the end creates eight possible combinations:

As eight stages of transformation of pure yang (Heaven trigram) into pure yin (Earth trigram), they can be represented in Figure 7 by an eight-cornered flow chart. The Tai Chi Tu, the ancient symbol of the polar opposites of yin and yang, is its equivalent.

     

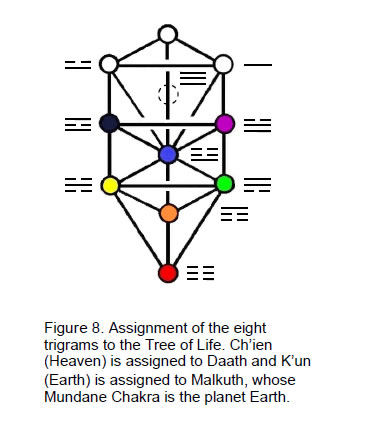
The eight trigrams can be formally assigned to Daath and the seven Sephiroth of Construction of the Tree of Life (Fig. 8), with the unbroken line (symbol of yang) assigned to Chokmah at the head of the Pillar of Mercy, which embodies the generative/active/male principle in Nature, and with the broken line (symbol of yin) assigned to Binah at the head of the Pillar of Judgement embodying the formative/reactive/female principle. The trigrams can be paired in (8²=64) ways. The resulting table of 64 pairs of trigrams (hexagrams) shown in Figure 9 was given algebraic, arithmetic & geometric interpretations in Articles 20 & 21.⁷ Its diagonal consists of the eight trigrams paired with themselves, i.e., the 48 yin/yang lines of the eight hexagrams comprise 24 yin lines and 24 yang lines. The 28 hexagrams in the upper half of the table consist of 56 trigrams with (56×3=168) yin/yang lines. Similarly, the 28 hexagrams in the lower half, which are the inversions of those in the upper half, comprise 168 yin/yang lines. Hence, the 384 yin/yang lines in the 64 hexagrams consist of

9

---

192 yin lines and 192 yang lines. Each diagonal half of the table comprises 96 yin lines and 96 yang lines. Of these, 12 yin lines and 12 yang lines make up the eight trigrams in the diagonal that are associated with each half and 84 yin lines and 84 yang lines make up the 56 off-diagonal trigrams. Each of the eight trigrams is repeated seven times in the 28 off-diagonal hexagrams, so that the number of yin/yang lines is 7×8×3 = 7×24, i.e., there are seven copies of the eight trigrams composed of 24 yin/yang lines.

We see that the I Ching table displays the following divisions and factorisations:

192 = 24 + 168 = 64×3;
24 = 8×3;
168 = 56×3 = 84×2 = 7×24.

Comparing them with the geometrical composition of the inner Tree of Life, we see that the 384 yin/yang lines correspond to the 384 geometrical elements of the two sets of seven separate Type A polygons. The 192 lines in each half of the table correspond to the 192 geometrical elements in each set. The 24 yin/yang lines in the eight diagonal trigrams of each half correspond to the 24 geometrical elements in the hexagon in each set, the 84 vertices & triangles and the 84 edges in the remaining polygons corresponding to the 84 yang and 84 yin lines in the 56 off-diagonal trigrams in each half of the table. These 56 triplets of yin/yang lines are the counterparts of the three sets of 56 elements in the polygons other than the hexagon. The seven copies of the eight trigrams correspond to the seven sets of 24 elements making up these polygons.  

When the polygons are Type B, the 384 yin/yang lines correspond to their 384 edges & triangles. The 24 yin/yang lines in a set of trigrams making up the upper or lower half of the diagonal correspond to the 24 outer edges of polygons in, respectively, S or S'. The 168 off-diagonal yin/yang lines in each half correspond to the 168 edges & triangles in S or S'. Their division into 56 trigrams is the counterpart of the 56 groups of three edges & triangles into which S and S' can be divided. Their division into 84 yin lines and 84 yang lines corresponds to the 84:84 division of edges & triangles in S or S'. Their seven copies of 24 yin/yang lines in a set of eight trigrams correspond to the seven edges & triangles per sector in S and S', each of whose three polygons has 24 sectors.

The 384 yin/yang lines in the 64 hexagrams of the I Ching table therefore symbolize the 384 geometrical elements of the two sets of Type A polygons making up the inner Tree of Life and the 384 edges & triangles in each set of Type B polygons. Each is an example of a holistic system characterized by the same set of parameters and displaying the same patterns of division and factorisation. It is highly implausible that this could be coincidental. This is confirmed by the emergence of analogous patterns in the seven musical scales, as next explained.

3. The 64×3 pattern in the intervals of the seven musical scales

The octave of the modern equal-tempered musical scale is divided into 12 equal semitones. Its progenitor was the Pythagorean scale, an eight-note scale whose notes have the tone ratios:  

1	9/8	81/64	4/3	3/2	27/16	243/128	2
T	T	L	T	T	T	L

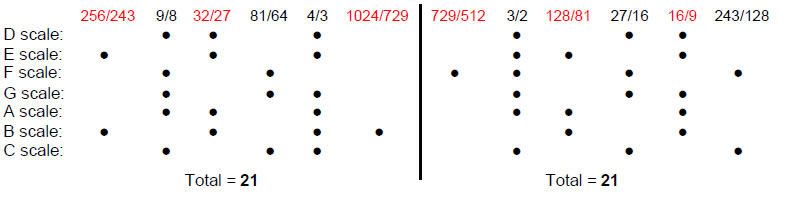
and are separated by five tone intervals T = 9/8 and two leimmas L = 256/143. Taking successive notes as the starting note, or tonic, generates seven possible musical scales. They are the four authentic modes: Dorian (D scale), Phrygian (E scale), Lydian (F scale) & Mixolydian (G scale); and the three plagal modes: Hypodorian (A scale), Hypophrygian (B scale) & Hypolydian mode (C scale). The fourth plagal mode (Hypomixolydian) is identical to the Mixolydian in terms of its sequence of intervals. Table 3 lists the tone ratios of the notes of the seven scales (red fractions denote notes not belonging to the Pythagorean scale (C scale).

Table 3. The tone ratios of the seven musical scales.

Musical scale	Tone ratio
B scale (Hypophrygian mode)	1	256/243	32/27	4/3	1024/729	128/81	16/9	2
A scale (Hypodorian)	1	9/8	32/27	4/3	3/2	128/81	16/9	2
G scale (Mixolydian)	1	9/8	81/64	4/3	3/2	27/16	16/9	2
F scale (Lydian)	1	9/8	81/64	729/512	3/2	27/16	243/128	2
E scale (Phrygian)	1	256/243	32/27	4/3	3/2	128/81	16//9	2
D scale (Dorian mode)	1	9/8	32/27	4/3	3/2	27/16	16//9	2
C scale (Hypolydian mode)	1	9/8	81/64	4/3	3/2	27/16	243/128	2

The 42 notes between the tonic and octave comprise 26 Pythagorean notes and 16 non-Pythagorean

10

---

notes. The Godname YAHWEH with number value 26 prescribes the Pythagorean character of the seven scales. The inversion of an interval n is the interval 2/n between it and the octave. For example, the perfect fifth with tone ratio 3/2 is the inversion of the perfect fourth with tone ratio 4/3 because 2/(4/3) = 3/2. Only the Dorian mode is made up of notes and their inversions. Table 3 indicates that the seven musical scales are composed of 14 types of notes:

1

256/243

9/8

32/27

81/64

4/3

1024/729

729/512

3/2

128/81

27/16

16/9

243/128

2

(the vertical line separates notes from their inversions). They consist of seven pairs of notes and their inversions, each pair of intervals spanning an octave. A note and its inversion are equidistant from the ends of the scale. In order of increasing magnitude, they are:

1.		1	2	T5L2	1×2 = 2
2.	L	256/243	243/128	T5L	256/243×243/128 = 2
3.	T	9/8	16/9	T4L2	9/8×16/9 = 2
4.	TL	32/27	27/16	T4L	32/27×27/16 = 2
5.	T2	81/64	128/81	T3L2	81/64×128/81 = 2
6.	T2L	4/3	3/2	T3L	4/3×3/2 = 2
7.	T2L2	1024/729	729/512	T3	1024/729×729/512 = 2

The 14 notes consist of two pairs of Pythagorean notes, four pairs of a Pythagorean and a non-Pythagorean note and one pair of non-Pythagorean notes, i.e., eight Pythagorean and six non-Pythagorean notes. Twelve types of notes make up the 42 notes between the tonic and octave of the seven scales. They comprise six Pythagorean notes and six non-Pythagorean notes. The 13 rising intervals above the tonic are mirrored by 13 corresponding falling intervals with tone ratios that are the reciprocal of those of the former. The number value 26 of YAHWEH is the number of different rising and falling tone intervals in the 14 types of notes. Consistent with its meaning of prescribing the domain of a holistic system, YAHWEH prescribes the intervallic range of the notes of the seven scales. The same 13:13 division is found in the semi-regular convex polyhedra, which consist of 13 Archimedean solids and their duals, the 13 Catalan solids.⁸ The duality of these polyhedra corresponds to the rising and falling distinction between intervals separating the types of notes that belong to the seven musical scales.

According to Table 3, the 42 notes between the tonic and octave divide equally into two sets of 21 notes and their 21 inversions:

Notice that the number of times the inversion of a note occurs is the same as the number of times the note does, although it does not always appear in the same scale — only the Dorian mode (D scale) has this property because it is composed solely of notes and their inversions. The number of notes for which their inversions do occur in the same scale is 15, showing how the Godnames EHYEH with number value 21 and YAH with number value 15 prescribe the notes in the seven scales. Notice also that the perfect fourths and perfect fifths occur most frequently. The letter value 1 of A (aleph) in the Hebrew Godname AHIH denotes the single pair of notes (1024/729, 729/512), the letter value 5 of H (heh) denotes the two pairs (256/243, 243/128) & the three pairs (81/64, 128/81), the letter value 10 of I (yod) denotes the four pairs (32/27, 27/16) & the six pairs (4/3, 3/2) and the letter value 5 of the second H denotes the five pairs (9/8, 16/9). No other assignment is possible.

There are 28 intervals between the eight notes of a musical scale, i.e., 27 intervals below the octave. The seven scales have (7×27=189) such rising intervals and 189 falling intervals, that is, 378 rising & falling intervals. The number 378 is the 26th triangular number after 1:

1 + 2 + 3 + … + 27 = 378.

It shows how YAHWEH with number value 26 prescribes the number of rising and falling intervals between the notes of the seven scales, as well as the number of their Pythagorean notes. The 189 intervals below the octave are therefore made up of 21 notes and 168 intervals that comprise their 21 inversions and 147 intervals between the seven notes above the tonic in the seven scales. Figure 10

11

---

displays the composition of the 189 intervals.⁹ They comprise 123 Pythagorean intervals and 66 non-Pythagorean intervals. The 125 intervals up to 1024/729 comprise 83 Pythagorean and 42 non-Pythagorean intervals. They have 64 inversions made up of 40 Pythagorean and 24 non-Pythagorean intervals. There are 63 pairs of intervals and their inversions and 63 unpaired intervals, that is, 63 triplets of intervals, each  triplet comprising a pair of intervals and an unpaired  interval. Of the 63 pairs, 21 are pairs  of notes and their inversions and 42 are pairs of intervals other than notes or their inversions. Altogether, the 189 intervals comprise 21 notes that are paired with their inversions, 84 paired intervals, 21 inversions of the notes and 63 unpaired intervals, i.e.,

84 intervals that are either inversions of notes or unpaired intervals. The 168 intervals other than the 21 notes up to 1024/729 therefore divide into two sets of 84 intervals. Their composition is:

	interval	number	interval	number
84:
	256/243	2	243/128	2
	9/8	5	16/9	5
	32/27	8	27/16	8
	81/64	6	128/81	6
	4/3	18	3/2	18
	1024/729	3	729/512	3
	Total =	42	Total =	42
84:
	256/243	10	243/128	2
	9/8	25	16/9	5
	32/27	12	27/16	4
	81/64	9	128/81	3
	4/3	6	3/2	6
	1024/729	0	729/512	2
	Total =	62	Total =	22

The 168 intervals trivially divide into seven groups of 24 intervals because there are 24 intervals in each scale other than the 21 notes tabulated earlier that have 21 inversions.

As the scales contain the same tonic and octave, as well as the 63 triplets of intervals, there is a final triplet consisting of two notes (the tonic and its inversion, the octave) and the generic interval of the octave. Hence, all possible rising intervals between the notes of the seven scales consist of 64 triplets. Formally speaking, it is meaningful to distinguish the rising and falling intervals between the tonic and itself even though they are both 1 in magnitude. The falling interval between the tonic and octave is ½, which is also the generic falling octave interval. All possible falling intervals consist of 64 triplets. Hence all possible rising and falling intervals between the notes of the seven scales comprise 64 triplets and, so to speak, their 64 ‘inverses.’

This double 64×3 pattern was found in the discussion of both the inner Tree of Life and the I Ching table, The 192 yin/yang lines in the upper, diagonal half of the latter signify the 192 rising intervals between the notes of the seven scales, with the three lines of the upper Heaven trigram in the diagonal symbolizing

12

---

the rising interval of 1 between the tonic and itself, the octave and the rising octave interval of 2. The 192 yin/yang lines in the lower, diagonal half of the table denote the 192 falling intervals, with the three lines of the lower Heaven trigram in the diagonal symbolizing the falling interval 1 between the tonic and itself, the falling octave interval of ½ and the generic falling octave interval of ½. The 21 yin/yang lines in the seven remaining diagonal trigrams in the upper half of the table signify the 21 notes, whilst the 21 lines in their counterparts in the lower half denote the 21 inversions of these notes. The 168 off-diagonal yin/yang lines in each half denote the 168 rising intervals other than these notes and their 168 falling counterparts. Their sevenfold repetition corresponds to the seven types of musical scales.

4. The 64×3 pattern in the Sri Yantra

Mandalas have been used by Hindus and Buddhists as objects of meditation and as spiritual teaching tools. Yantras are the yogic equivalent of these plans or charts that symbolize the cosmos — both physical and spiritual. The Sri Yantra is the most revered as the mother of all Yantra. Mapping man’s inward journey from physical existence to spiritual enlightenment, its system of interlocking triangles is surrounded by a lotus of eight petals, a lotus of sixteen petals, and an earth square resembling a temple with four doors. The Sri Yantra (Fig. 11) is generated from nine primary triangles. Five downward-pointing triangles symbolizing the feminine, creative energy of the Goddess Shakti intersect four upward-pointing triangles symbolizing the masculine, creative energy, popularly conceived in India as the God Shiva. Their overlapping generates 43 triangles. 42 triangles arranged in four layers of eight, ten, ten and 14 triangles surround a downward pointing triangle whose corners denote the triple Godhead, or Hindu Trimûrti, of Shiva, Brahma and Vishnu. At its centre is a point, or ‘bindu,’ representing the Absolute, or transcendental unity. Including its square enclosure and two sets of circumscribing lotus petals, the Sri Yantra has nine levels.

There are two ways of conceiving the set of 43 triangles. The more common one is to regard them as lying in the same plane, so that outward-pointing vertices of triangles touch either the bases or vertices of triangles in the adjacent, surrounding set. When their geometrical composition is analysed, this means that the vertices of some triangles meet at a single point in this plane, whilst other vertices lie on edges of triangles. The other way is to regard the Sri Yantra as a three-dimensional stack of four layers of triangles, so that only triangles in the same layer touch one another. Both cases were analyzed in Article 35,¹⁰ where the equivalence of the Sri Yantra and the inner form of the Tree of Life was established. In this article, we shall focus on only one of the features of the three-dimensional Sri Yantra.

As representations of the Divine Whole, the Tree of Life is equivalent to the tetractys (Fig. 12). This is a triangular array of ten points that had a special role in the number mysticism of the ancient Pythagoreans. Because the yod (י), the tenth letter of the Hebrew alphabet, looks somewhat like a dot, these points will be called yods. The Supernal Triad of Kether, Chokmah & Binah correspond to the three yods at the corners of the tetractys. The seven Sephiroth of Construction correspond to the seven ‘hexagonal yods,’ so-called because they are located at the corners and at the centre of a hexagon. Malkuth corresponds to the central hexagonal yod and the two triads of Sephiroth of Construction: Chesed-Geburah-Tiphareth & Netzach-Hod-Yesod correspond to the hexagonal yods at the corners of two equilateral triangles intersecting to form a Star of David (known in Hinduism as the ‘Sign of Vishnu’). When it is constructed out of the template of the tetractys, an object possessing sacred geometry is turned into a set of numbers, namely, the numbers of various classes of yods that mark out its structure in space. As many previous articles have demonstrated, these numbers characterize holistic systems like the superstring and the seven musical scales.

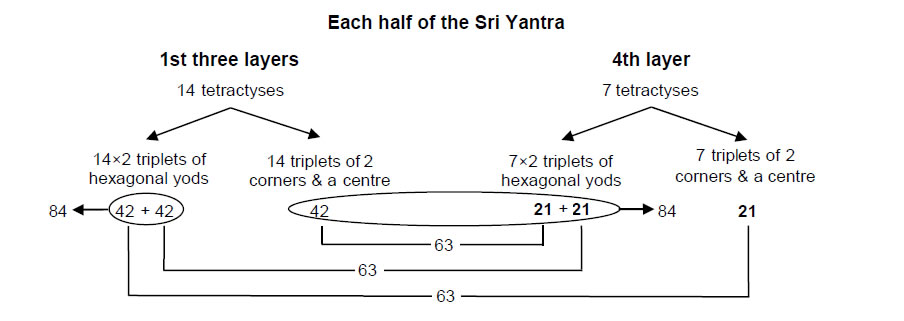
When the 42 triangles surrounding the central triangle in the Sri Yantra are turned into tetractyses, 378 yods are generated (Fig. 13). 42 hexagonal yods are at the centres of the 42 tetractyses, which have 84 yods at corners (42 in each half of the Sri Yantra) and 252 hexagonal yods lie on their 126 edges. Hence, there are 189 yods in each half that are made up of 21 hexagonal yods at centres of tetractyses and (42+126=168) yods lining their edges.

 

 

13

---

14

---

It might seem natural to assign: 1. the 21 note intervals and their falling counterparts in the seven musical scales to the hexagonal yods at the centres of the set of 21 tetractyses in each half of the Sri Yantra, and 2. the remaining 168 rising intervals and their falling counterparts to the 168 yods on their edges. However, the analogous 21:168 division of the I Ching table tells us that 21 yods in the Sri Yantra must consist of seven triplets corresponding to the seven upper trigrams in the diagonal hexagrams other than the Heaven trigram. The 63 triplets of yods in each half of the Sri Yantra consist of 42 triplets of hexagonal yods at corners of two intersecting triangles within each triangle and 21 triplets of yods at the corners and centres of triangles. The latter divide up uniquely into 14 triplets in the first three layers of triangles and seven triplets in the fourth layer:

The seven upper trigrams correspond to the seven triplets of corners & centres of the triangles in one half of the fourth layer, the seven lower trigrams corresponding to the corners and centres of the seven triangles in its other half. Can their counterpart 21 notes actually be grouped into seven sets of three, as required? Yes, uniquely, according to Fig. 10:

The three sets of seven notes can be thought of as seven sets of three, one being drawn from each set of seven (similarly for their inversions). The composition of the 189 rising intervals was found in the previous section to be:

21 notes + 42 intervals & their 42 inversions + 21 inversions of notes + 63 unpaired intervals.

The 42 intervals and their 42 inversions are assigned to the 14 pairs of intersecting triplets of hexagonal yods in the 14 tetractyses of the first three layers in half of the Sri Yantra, whilst the 21 inversions of notes and the 63 unpaired intervals are assigned, respectively, to the 21 hexagonal yods in seven triplets of the seven triangles in the fourth layer and to the 63 yods that are either at corners & centres of the 14 tetractyses in the first three layers or in the seven other triplets of hexagonal yods in the seven tetractyses of the fourth layer. The 189 falling intervals are similarly assigned to their diametrical opposites in the other half of the Sri Yantra. The (42+42=84) hexagonal yods forming triplets in the first three layers denote the 42 intervals and their inversions. The 168 yods other than the 21 corners & centres of the seven tetractyses in the fourth layer in each half of the Sri Yantra symbolize the 168 rising intervals and the 168 falling intervals other than the primary 21 notes up to that with tone ratio 1024/729. Just as the 168 intervals are divided into two sets of 84, so the 168 yods split into two sets of 84, as shown in the diagram above.

Viewed as a tetractys, the central triangle has six hexagonal yods on its edges arranged at the corners of a Star of David. The musical counterparts of the two intersecting triangles are: 1. the tonic, octave & rising octave interval, and 2. the unit interval, the octave ½ and the falling octave interval of ½. As the source of the holistic system that is the seven musical scales, these intervals express in potentia the musical domain of rising and falling intervals represented by the 378 yods of the 42 tetractyses that surround the central one. Hence, the 378 yods in the 42 tetractyses, together with the two triplets of hexagonal yods in the central triangle, are composed of 64 triplets and their 64 inverses, reflected across its centre. This double 64×3 pattern is exactly the same as that shown by the 64 trigrams belonging to each diagonal half

15

---

of the I Ching table (see Fig. 13). The correspondence between the Sri Yantra and I Ching table is shown below:

	I Ching table	Sri Yantra
1.	two Heaven trigrams of hexagram in top left-hand corner	→ two triplets of hexagonal yods in central triangle;
2.	21 yin/yang lines in 7 other diagonal trigrams in each half	→ 21 corners & centres of triangles in the 7 triangles;
3.	168 yin/yang lines in 28 off-diagonal hexagrams in each half	→ 168 yods other than 21 corners & centres;
4.	64 trigrams in each half	→ 64 triplets of yods in each half;
5.	192 yin/yang lines in each half	→ 192 yods in each half;
6.	384 yin/yang lines in 64 hexagrams	→ 384 yods in 64 pairs of triplets.

The counterparts in the inner Tree of Life of the 192 yods making up each half of the Sri Yantra are the 192 vertices, edges & triangles surrounding the centres of the two sets of seven Type A polygons discussed in Section 1, which we saw can be grouped into 64 sets of three (p. 6). The 24 yin/yang lines in the eight upper or lower trigrams in the diagonal of the I Ching table correspond to the 24 geometrical elements surrounding the centre of the hexagon in each set. The 168 off-diagonal yin/yang lines in each half of the table correspond to the 168 geometrical elements

surrounding the centres of the six remaining regular polygons in each set. They are present in 56 trigrams, which correspond to the 56 triplets of elements in these polygons. The 48 geometrical elements in the pair of hexagons are the counterparts of the 48 yin/yang lines in the eight diagonal hexagrams and of the 48 yods either at centres or corners of tetractyses in the fourth layer of the Sri Yantra or on edges of the central tetractys. As we shall further illustrate, this 48:336 division is characteristic of the 384 degrees of freedom displayed by holistic systems. So also is their 2×64×3 factorisation. The factor of 2 arises because they consist of two halves that are mirror images or inverses of each other — the two sets of seven polygons, the two halves of the I Ching table and the Sri Yantra and the rising and falling aspects of every interval. 

The factor of 3 stems from the way in which the 192 geometrical elements surrounding the centres of the seven polygons can be naturally grouped into three sets, from the trigrams, from the grouping of the musical intervals into three sets (paired notes/intervals and unpaired intervals) and from the grouping into triplets of, firstly, the two corners per tetractys and its centre and, secondly, the Star of David formed by hexagonal yods on edges of tetractyses.

16

---

5. The 64×3 pattern in the disdyakis triacontahedron

There are 13 convex, semi-regular polyhedra. Called the ‘Archimedean solids,’ their counterparts generated by replacing vertices by faces and vice versa are called the ‘Catalan solids.’ The Catalan solid with the most number of vertices is the disdyakis triacontahedron (Fig. 14). It has 62 vertices, 180 edges & 120 triangular faces. 12 vertices (called ‘B’) are the vertices of a icosahedron and 20 vertices (called ‘C’) are vertices of a dodecahedron. The 32 B & C vertices belong to the rhombic triacontahedron (Fig. 15), which has 30 Golden Rhombic faces, the ratios of whose diagonals (edges of the icosahedron & dodecahedron) is the Golden Ratio φ, considered for hundred of years by artists and architects as a proportion most pleasing to the human eye. The apices of the 30 pyramids having these faces as their bases are called ‘A’ vertices.

It was proved in previous articles^11,12,13 that the disdyakis triacontahedron is the polyhedral version of the Tree of Life. More generally, it is the polyhedral manifestation of the archetypal pattern intrinsic to all holistic systems. The surface of this Catalan solid has 362 geometric elements. This attribute is encoded in the pair of Type B dodecagons — the last of the regular polygons making up the inner Tree of Life — because the division of their 24 sectors into three tetractyses produces 362 yods (Fig. 16). Each yod denotes a geometric element. The two centres denote any pair of diametrically opposite A vertices and the 360 yods surrounding them denote the 60 vertices, 180 edges and 120 triangles between these opposite poles.

The 181 yods in each dodecagon denote the 181 geometrical elements in each half of the disdyakis triacontahedron. The archetypal ‘form’ quality of the Godname ELOHIM assigned to Binah in the Tree of Life is illustrated by the fact that its number value 50 is the number of corners of the 72 tetractyses in the pair of dodecagons. The same applies to the Godname ELOHA assigned to Geburah below Binah because its number value is 36, which is the number of tetractyses in a dodecagon.

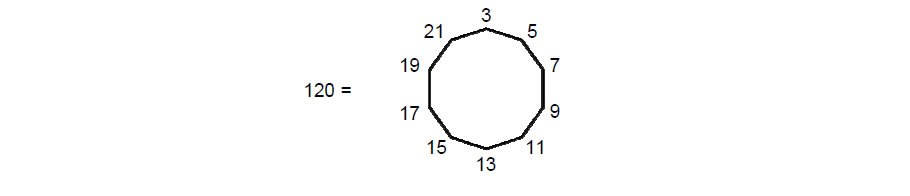
The Decad (10) determines geometrical properties of the disdyakis triacontahedron because it has: 1. 120 triangles, where 120 is the sum of the first 10 odd integers after 1 that can be assigned to the corners of the decagon:

2. 60 vertices surrounding an axis of the polyhedron passing through two diametrically opposite vertices,

17

---

where 60 is the number of hexagonal yods in a Type A dodecagon, the tenth regular polygon, and 3. 180 edges, where 180 is the number of yods surrounding the centre of a Type B dodecagon (Fig. 16).

Suppose that we choose as the Z-axis one of the 15 possible lines joining two opposite A vertices. Figure 17a shows the projection onto the XY plane of the 62 vertices. They are located on seven sheets. Three sheets are above or below the central one in the XY plane. The 12 vertices and 12 edges lying in the latter form a 12-sided polygon (Fig. 17b). They comprise four A vertices, four B vertices, four C vertices, four AB edges, four BC edges & four AC edges. In other words, there are three types of vertices, each repeated four times, and three types of edges, each repeated four times. These are indicated in Fig. 17b by the three black lines of different thicknesses, their diametrically opposite counterparts being yellow lines. There are 84 polyhedral edges either above or below the central polygon with 12 edges, which are also polyhedral edges. The 12 sectors of the polygon have 12 internal edges (coloured purple in three thicknesses, the lines opposite them being light purple, with pairs of diametrically opposite sectors coloured in light and dark shades of red, blue & violet). If O is the centre of the polygon, there are four OA edges, four OB edges and four OC edges. Hence, there are 192 edges, 24 belonging to the central polygon and grouped into eight triplets of edges and 168 belonging solely to the polyhedron. The 180 edges comprise 60 AB edges, 60 BC edges and 60 AC edges. This means that the 168 edges comprise (60–4=56) edges of these three types. They are divided into 28 AB, 28 BC & 28 AC edges above the XY plane and their counterparts below it. The 192 edges are grouped into 64 edges, each of three types, eight belonging to the central polygon and 56 belonging solely to the polyhedron.

Each edge can be regarded as a double-headed arrow, i.e., as arrows that point in opposite directions. If we write the arrow pointing from A to B as E_A, the arrow pointing from B to C as E_B and the arrow pointing from C to A as E_C, the arrow pointing from B to A is –E_A, etc. Similarly, the arrow AO pointing from A to O is e_A and the arrow OA pointing from O to A is –e_A (similarly for vertices B & C). Using primes to indicate the repeated set of vertices & edges, there are four triplets of arrows:

AB = EA	AO = eA	A'B' = EA'	A'O = eA'
BC = EB	BO = eB	B'C' = EB'	B'O = eB'
CA = EC	CO = eC	C'A' = EC'	C'O = eC'

and four triplets of their counterparts pointing in the opposite direction. There are 384 arrows comprising 168 arrows either above or below the central polygon, each made up of two sets of 28 groups of three arrows, and 48 arrows belonging to the latter, which are further divided into two sets of 24, each set consisting of eight triplets. 192 arrows point along the edges of each half of the polyhedron and sectors of its central polygon.

This pattern of two sets of 64 triplets of arrows is identical to the 64 pairs of trigrams in the I Ching table. The two possible opposite directions of each arrow are the counterparts of the yin and yang polarities of each line in a trigram. The pairing of similar trigrams in the diagonal of the table represents the fact that every set of three arrows belonging to one half of the central polygon has its inverted counterpart in its other half. In the case of the 384 geometrical elements of the two sets of seven polygons constituting the inner Tree of Life, we found that the 24 geometrical elements in one hexagon have their mirror image counterparts in the hexagon belonging to the other set. The inversion of pairs of trigrams in opposite diagonal halves of the table corresponds to the counterparts of their arrows being spatially inverted in the other half of the polyhedron. What makes the disdyakis triacontahedron holistic is that it is the polyhedral representation of all 64 possible pairs of eight trigrams when yin and yang lines are identified as the orientated edges of its faces and sectors of its central polygon.

The 168 edges of the disdyakis triacontahedron above and below the central polygon divide into 56 groups of three because all edges are of three types. They divide into 84 edges above the polygon and 84 edges below it, that is, into two sets of seven groups of 12 edges, a group consisting of four triplets of AB, BC & AC. The 168 arrows either above or below the XY plane consist of seven groups of 24 arrows, a group comprising eight triplets of arrows. This is the same as the seven sets of trigrams either above or below the diagonal of the I Ching table. The disdyakis triacontahedron exhibits the same 56×3, 84×2 & 7×24 as found earlier for the inner Tree of Life, the seven musical scales and the I Ching table.

6. The 64×3 pattern in the {3,7} tessellation of the 3-torus

The Klein quartic
Felix Klein (1849–1925) is well-known to mathematicians as one of the nineteenth century’s great geometers. The one-sided, closed surface called the “Klein bottle” is named after him. In 1878, he discovered that the curve:

X³Y + Y³Z + Z³X = 0,

18

---

where X, Y & Z are complex numbers, has the 336-fold symmetry of the group SL(2,7), the special, linear group of 2×2 real matrices with determinant 1 over a field of order 7. This curve is known as the “Klein quartic.” The “Klein surface” is the Riemann surface of the Klein quartic. Klein showed that it is mapped onto itself (hence “automorphisms”) by 168 analytic transformations. Hurwitz showed that a Riemann surface of genus g has at most 84(g–1) automorphisms and the same number of anti-automorphisms. A Riemann surface with the maximum number of automorphisms is called a “Hurwitz curve” of genus g (g≥3). A Hurwitz curve of genus 3 has 84(3–1) = 84×2 = 168 automorphisms. The Klein curve is the Hurwitz curve with the smallest genus g = 3.

A regular tessellation, or tiling, is a covering of the plane by regular polygons so that the same number of polygons meets at each vertex. The Schläfli symbol {n,k} is the tessellation by polygons with n vertices, k polygons meeting at each vertex. If 1/n + 1/k < 0, {n,k} is a tessellation of the hyperbolic plane with negative curvature. If 1/n + 1/k = 0, {n,k} is a tessellation of the Euclidean plane with zero curvature. If 1/n + 1/k > 0, {n,k} is a tessellation of the elliptic plane with positive curvature.

The regular tessellations of the Euclidean plane are well-known. They are: {3,6} in which equilateral triangles meet six at each vertex; {4,4} in which squares meet four at each vertex; and {6,3} in which hexagons meet three at each vertex. The mathematician Poincaré described ways in which points in the hyperbolic plane can be represented conformally in the Euclidean plane. One of them is to represent the hyperbolic plane by points within the so-called ‘Poincaré disk’. {n,k} is the Poincaré dual of {k,n} in which vertices and polygons are interchanged.

The {3,7} tessellation of the 3-torus
SL(2,7) is the double-cover of the Klein quartic symmetry group PSL(2,7). Its order 336 is the number of automorphisms and anti-automorphisms of the Klein quartic. The 168 elements of PSL(2,7) are represented either by the {7,3} tiling of the Poincaré disk with 24 heptagons having 168 vertices or by its {3,7} tiling with 56 triangles having 168 vertices (Fig. 18). The Riemann surface of the Klein quartic is a 168-sheeted covering of the sphere, branched over three points of the sphere:

• Above one of these points, the 168 sheets join in groups of seven to give 24 points of the surface. These are the points of inflection of the curve described by the Klein quartic. They are also what are called the “Weirstrass points.” The 24 orbits of subgroups of order 7 correspond to these points.

• Above another branch point, there are 84 points of the surface, where the sheets join in twos. These are the sextactic points through which pass a conic section that has six-fold contact with the curve. The 84 orbits of subgroups of order 2 correspond to them.

• Above the third branch point, the sheets join in threes to give 56 points of the surface. These 56 points are the points of contact of the Klein quartic with the 28 bitangents, or lines that are tangent to the curve at two points. The 56 orbits of subgroups of order 3 correspond to them.

Having genus 3, the hyperbolic, Riemann surface of the so-called ‘Klein Configuration’ can be embedded

19

---

on the surface of a 3-torus (Fig. 19a), which has the same genus because it is topologically equivalent to a sphere with three handles attached to it. The 3-torus is also topologically equivalent to six square antiprisms with their 12 square faces stuck to the 12 square faces of four triangular prisms in a tetrahedral formation, each antiprism being given a twist¹⁴ (Fig. 19b). This leaves 56 triangular faces, which, as separate triangles, have 168 vertices (eight faces from the triangular prisms with 24 vertices, 48 faces from the square antiprisms with 144 vertices). Each triangular prism has nine edges and each square antiprism has 16 edges, of which eight edges coincide with edges of the former when they are stuck together, resulting in (4×9 + 6×8 = 84) edges of triangles. Figure 19b shows the {3,7} tessellation onto the 3-torus of the 56 orbits of order 3 corresponding to the 56 bitangent points of the Klein quartic. The 168 anti-automorphisms of the Klein quartic have a {3,7} tiling on a 3-torus that is turned inside-out. As discussed in Article 43,¹⁵ the 24 vertices and 84 edges of the 56 triangles in the tetrahedral-deformed 3-torus and the 24 vertices and 84 edges in its turned inside-out version are the respective counterparts of the 24 vertices and 84 edges above the central plane of the disdyakis triacontahedron that surround an axis joining two opposite A vertices and the mirror images of these vertices and edges below this plane. Indeed, a one-to-one correspondence was shown to exist between the geometries of the polyhedron and this pair of 3-tori. As the former is the polyhedral form of the inner Tree of Life, the {3,7} tessellation of the 168 automorphisms of the Klein quartic onto the 3-torus constitutes a holistic pattern that is isomorphic to all sacred geometries. The aspect of this equivalence that is relevant to this article will be discussed next.

{3,7} tessellation of 3-torus with tetractyses
Consider the triangular faces of the triangular prisms and the square antiprisms making up the 3-torus, firstly, turned into tetractyses and, secondly, divided into their three sectors and the latter then turned into tetractyses (i.e., Type A triangles with tetractyses as their sectors). Their square faces must be ignored because they are not part of the surface of the 3-torus. We shall calculate the numbers of yods in each case, noting that the 12 squares of the prisms become stuck to the 12 squares of the antiprisms, so that they play no part in the properties of the surface of the 3-torus.

The geometrical elements making up the two types of prisms are listed below:

A triangular prism has 6 vertices, 9 edges, 2 triangles & 3 squares.
A square antiprism has 8 vertices, 16 edges (8 unshared), 8 triangles & 2 squares.

Table 4. Geometrical & yod composition of the 56 triangles in the {3,7} tessellation of the 3-torus.

	Tetractys			Type A triangle
	triangular prism	square antiprism	Total	triangular prism	square antiprism	Total
Number of vertices	4×6=24	—	24	24+8×1=32	48×1=48	80
Number of edges	4×9=36	6×8=48	84	36+8×3=60	48+48×3=192	252
Number of triangles	4×2=8	6×8=48	56	8×3=24	48×3=144	168
Number of geometrical elements	68	96	164	116	384	500
Number of hexagonal yods on edges of tetractyses	2×36=72	2×48=96	168	2×60=120	2×192=384	504
Number of hexagonal yods	8+72=80	48+96=144	224	24+120=144	144+384=528	672
Number of yods on edges of tetractyses	24+72=96	96	192	32+120=152	96+384=432	584
Number of yods	8+96=104	48+96=144	248	24+152=176	144+432=576	752

20

---

The four triangular prisms have 24 vertices and the six square antiprisms have 48 vertices.

Let us now consider them joined together at their square faces to form the 3-torus. Let us also regard them as tetractyses. Table 4 displays their geometrical and yod composition. With single tetractyses as their faces, the four triangular prisms and the six square antiprisms are composed of 56 tetractyses with 248 yods (see pink cell). This is very remarkable, for 248 is the number of E₈ gauge bosons that transmit the unified force between superstrings of ordinary matter! Furthermore, the 248 yods comprise eight yods at centres of the faces of the four triangular prisms, leaving 240 yods made up of 24 yods at vertices, 48 hexagonal yods at centres of tetractyses (i.e., 72 yods that are either vertices or centres) and 168 hexagonal yods on their 84 edges (see green cell). The division:

248 = 8 + 240

corresponds to the eight simple roots of E₈ and its 240 roots. The division:

240 = 72 + 168

corresponds to the 72 roots of E₆, an exceptional subgroup of E₈, and the 168 remaining roots of E₈. The root structure of the superstring gauge symmetry group E₈ is embodied in the yod composition of the tetractyses tessellating the 3-torus! As was so often found in previous articles, the number 168 defines the shape of the holistic system. Here — in the case of faces as single tetractyses — it is the number of hexagonal yods on the boundary of the tetractyses that compose it. In the case of Type A faces, it is the number of triangles. The number 72 merely defines the corners and centres of the 56 tetractyses.

According to Table 4, 192 yods lie on the 84 edges of the 56 tetractyses. 24 yods are vertices of the four triangular prisms. The same applies for the 3-torus when it is turned inside-out. This 24:168 division corresponds in the inner form of the Tree of Life to the 24 geometrical elements that surround the centre of the hexagon and to the 168 geometrical elements surrounding the centres of the six other regular polygons (Fig. 20). It corresponds in the I Ching table to the 24 yin/yang lines of the eight upper trigrams in its diagonal and to the 168 yin/yang lines in the 56 trigrams above the diagonal. Its counterparts in the Sri Yantra are the 24 yods in each half that are either at centres of tetractyses or hexagonal yods in the central tetractys and the 168 yods lying on edges of tetractyses. The turned-inside out 3-torus, whose

21

---

{3,7} tessellation into 56 triangles map the 168 anti-automorphisms of the Klein quartic, is the counterpart of the mirror-image set of seven polygons in the inner Tree of Life and the lower diagonal half of the I Ching table. This implies that the 384 symmetries of the Klein quartic constitute a whole. Furthermore, (248+248=496) yods are needed to turn the (56+56=112) triangles of the two 3-tori into tetractyses. This demonstrates a connection with the (248+248=496) gauge bosons transmitting the forces between E₈×E₈ heterotic superstrings. Each yod symbolizes one of these messenger particles. Clearly, the double-cover nature of the group SL(2,7) of automorphisms and anti-automorphisms of the Klein quartic is related to the direct product nature of the heterotic superstring gauge symmetry group E₈×E₈. The question is: why?

The eight triangular faces of the four triangular prisms consist of eight sets of three vertices. They correspond to the eight upper trigrams in the diagonal of the I Ching table (like the latter, they are divided into two sets of four faces, each with three vertices). The 168 hexagonal yods on the edges of the ten prisms and antiprisms and belonging to 56 tetractyses are arranged as 56 sets of two interlaced triangular arrays of three yods shared between adjoining tetractyses, that is, as 28 independent sets of two arrays. They correspond to the 28 hexagrams with 168 yang/yin lines above the diagonal. Similarly, the 168 hexagonal yods lining edges of the 56 tetractyses in the turned inside-out 3-torus correspond to the 28 hexagrams with 168 yin/yang lines below the diagonal. The 84×2 factorisation of the 168 hexagonal yods arises from the fact that a pair of hexagonal yods lies on each of the 84 edges. They belong to oppositely interlaced triangles. This is the counterpart of the yin/yang duality of lines and broken lines in the trigrams. In the case of the 24 vertices of the triangular prisms, vertices belonging to their opposite triangular faces correspond to yin and yang lines. The 192 yods on edges of tetractyses in each 3-torus consist of (8+56=64) triplets. The eight triplets of vertices correspond to the 24 geometrical elements surrounding the centre of the hexagon in the inner Tree of Life. The counterpart here of the two sets of four triplets of vertices is the two sets of three successive sectors, each with four geometrical elements, which regroup into two sets of four triplets of elements.

The nine edges of the triangular prism consist of the three edges of each opposite triangular face and three edges that join vertices of these faces. Hence, they consist of three types of edges, each occurring three times. The four triangular prisms have three types of edges, each occurring 12 times. Two hexagonal yods lie on each edge. Therefore, there are 24 hexagonal yods on each of three types of edges. The square faces of the square antiprism are rotated relative to each other by 45°. Each vertex of one square face is joined to two vertices of the other square (Fig. 21). This means that the eight edges of the square antiprism that are not edges of squares divide into four primary sets of two edges. The six square antiprisms have 48 edges that group into four primary sets of 12 edges. As each edge has two hexagonal yods, the 96 hexagonal yods group into four sets of 24 hexagonal yods. Hence, the 168 hexagonal yods on the 84 edges of the prisms and antiprisms consist of 24 hexagonal yods on each of the three types of edges of the triangular prisms and on each of the four types of edges of the square antiprisms. In other words, there are seven classes of 24 hexagonal yods. This 7×24 division has its counterpart in the I Ching table as the seven copies of each trigram either above or below the diagonal, i.e., as the seven copies of the 24 yin/yang lines of the eight types of trigrams. Their counterparts in the

seven musical scales are the 24 inversions and intervals between notes in each scale. Their counterparts in the inner Tree of Life are the seven groups of 24 geometrical elements surrounding the centres of the polygons other than the hexagon (p. 6).

The 48 triangular faces of the six square antiprisms display the same 24:24 division as the 48 yin/yang lines of the eight hexagrams in the diagonal of the I Ching table. This is because the faces are of two

22

---

types — a downward-pointing face and an upward-pointing one. The 24 faces of the former type share edges with upper square faces like the light grey one shown in Fig. 21. The 24 faces of the latter type share edges with lower square faces. Upward and downward-pointing faces (depicted in Fig. 21 by two different shades of grey) embody the polarities of yin and yang. The six sets of (4+4) faces are the counterparts of the six yin/yang lines in each of the two sets of four diagonal hexagrams. The reason for this correspondence is that Table 4 shows that, when these faces are Type A triangles, there are 384 hexagonal yods lying on edges of tetractyses, 192 being on edges of downward-pointing tetractyses and 192 being on edges of upward-pointing tetractyses. They are the counterparts of the 192 yin lines and 192 yang lines in the table. This 192:192 division, which characterises holistic systems and which is present in the yods lining the edges of the tetractyses making up the 3-torus and its turned inside-out version, is also present in each 3-torus when the triangles are Type A. Indeed, this division manifests in the geometrical composition of the square antiprisms as well, for they have 384 geometrical elements, of which 48 are vertices (24 in upward-pointing triangles and 24 in downward-pointing ones) and 336 are edges & triangles (168 in upward-pointing triangles and 168 in downward-pointing ones). In other words, they comprise 192 ‘yin’ geometrical elements and 192 ‘yang’ geometrical elements. Alternatively, according to Table 4, whereas there are 384 yods lining the edges of the triangles in both 3-tori when they are tetractyses, there are 384 hexagonal yods lining the edges of tetractyses in the square antiprisms forming the ‘arms’ of either 3-torus. As we found in Section 1 for the Type A and Type B polygons of the inner Tree of Life, holistic parameters like 384 characterize not only the whole system at one level of differentiation but each half of it at another level. The whole system is both sets of seven polygons and both 3-tori. Holistic systems are binary because they have a cyclic quality that is divided into an outward, expansive (yang) phase and a returning, contractive (yin) phase that in some way is the mirror image, or reverse, of the former. One example is the 192 rising intervals and the 192 falling intervals between the notes of the seven musical scales; the 192 doubly-orientated edges of the disdyakis triacontahedron and the sectors of its central, 12-sided polygon are another example, one half being the mirror image of the other half in a spatial balance of yang and yin.

We have established that the tetractys transformation of the 56 hyperbolic triangles on the 3-torus reproduces the same 84×2, 56×3 & 24×7 divisions of yods as found in the 168 automorphisms of the Klein quartic, which form 84 subgroups of order 2 (sextactic points of its Riemann surface), 56 subgroups of order 3 (points of contact of bitangents) and 24 subgroups of order 7 (points of inflection). The symmetries of the equation contain the characteristic patterns of a holistic system as represented by sacred geometries and the seven musical scales.

7. The 64 codons

DNA is made of chemical building blocks called nucleotides. These building blocks are made of three parts: a phosphate group, a sugar group (2-deoxyribose, which is a pentose (five-carbon) sugar) and one of four types of nitrogen bases. To form a strand of DNA, nucleotides are linked into chains, with the phosphate and sugar groups alternating. The four types of nitrogen bases found in nucleotides are: adenine (A), thymine (T), guanine (G) and cytosine (C) (Fig. 22). The order, or sequence, of these bases determines what biological instructions are contained in a strand of DNA. For example, the sequence ATCGTT might instruct for blue eyes, while ATCGCT might instruct for brown. Each DNA sequence that

 

 

 

 

 

23

---

contains instructions to make a protein is known as a gene. The size of a gene may vary greatly, ranging from about 1,000 bases to 1 million bases in humans. The complete DNA instruction book, or genome, for a human contains about 3 billion bases and about 20,000 genes on 23 pairs of chromosomes. The largest human chromosome contains approximately 220 million base pairs.

To understand DNA’s double helix from a chemical standpoint, picture the sides of the ladder as strands of alternating sugar and phosphate groups — strands that run in opposite directions. Each “rung” of the ladder is made up of two nitrogen bases, paired together by hydrogen bonds (Fig. 23). Because of the highly specific nature of this type of chemical pairing, base A always pairs with base T, and likewise C with G. These rules of complementary base pairing are strictly followed because the four different sorts of nucleotides are different shapes, so in order for the strands to close up properly, an A nucleotide must go opposite a T nucleotide, and a G opposite a C.

DNA's unique structure enables the molecule to copy itself during cell division. When a cell prepares to divide, the DNA helix splits down the middle and becomes two single strands. These single strands serve as templates for building two new, double-stranded DNA molecules — each a replica of the original DNA molecule. In this process, an A base is added wherever there is a T, a C where there is a G, and so on until all of the bases once again have partners.

In addition, when proteins are being made, the double helix unwinds to allow a single strand of DNA to serve as a template. This template strand is then transcribed into messenger RNA, which is a molecule that conveys vital instructions to the cell's protein-making machinery.

The genetic code consists of (4×4×4=64) triplets of nucleotides called codons. With three exceptions, each codon encodes for one of the 20 standard amino acids used in the synthesis of proteins (humans can produce 10 of the 20 amino acids.¹⁶ The others must be supplied in the food). That produces some redundancy in the code: most of the amino acids are encoded by more than one codon.

The genetic code can be expressed as either RNA codons or DNA codons. RNA codons occur in messenger RNA (mRNA) and are the codons that are actually “read” during the synthesis of polypeptides (the process called ‘translation’). But each mRNA molecule acquires its sequence of nucleotides by ‘transcription’ from the corresponding gene. Figure 24 shows a typical short section of an mRNA.

RNA is a single-stranded molecule with a much shorter chain of nucleotides than DNA. Whereas DNA contains deoxyribose, RNA contains ribose, whose OH group makes it less stable than DNA. The complementary base to adenine is not thymine but uracil (U), an unmethylated form of thymine (compare their molecules in Fig. 22).

There are three ‘stop’ or ‘nonsense’ codons signifying the end of the coding region; these are the UAA, UAG, and UGA codons. Sixty-one codons code solely for amino acids. One codon (AUG) in mRNA serves two related functions:

• it signals the start of translation. Hence, it is called the start codon;

• it codes for the incorporation of the amino acid methionine into the growing polypeptide chain.

An anticodon is a sequence of three adjacent nucleotides in transfer RNA (tRNA) that correspond to the

 

 

 

 

 

24

---

three bases of the codon on the mRNA. An anticodon is complementary to the codon in messenger RNA that binds to it and designates a specific amino acid during protein synthesis at a ribosome. Each tRNA contains a specific anticodon triplet sequence that can base-pair to one or more codons for an amino acid.

In transcription, RNA is synthesized from the DNA template by an enzyme — RNA polymerase. The enzyme binds to a promoter sequence in the DNA, causing the double helix to unwind. The enzyme progresses along the template strand, synthesizing a complementary RNA molecule. In so-called ‘translation,’ messenger RNA (mRNA) carries information about a protein sequence to the ribosomes, which synthesize protein in the cell. Ribosomes are complexes of RNA and protein. Transfer RNA is a small RNA chain of about 80 nucleotides that transfers a specific amino acid to

a growing polypeptide chain at the ribosomal site of protein synthesis during translation. It has sites for amino acid attachment and an anticodon region that can base pair to the corresponding three-base codon region on mRNA through hydrogen binding. tRNA reads the sequence of the messenger RNA and is attached to the amino acids. Each type of tRNA can be attached to only one type of amino acid, but because the genetic code contains multiple codons that specify the same amino acid, tRNA molecules bearing different anticodons may also carry the same amino acid.

Table 5 lists the 64 codons in mRNA and the amino acids for which they code.

Table 5. The 64 codons (M-RNA base triplets) and the amino acid for which each codon codes.

Amino acid	2nd base
		U	C	A	G
1st base	U	UUU Phenylalanine  UUC Phenylalamine  UUA Leucine  UUG Leucine	UCU Serine  UCC Serine  UCA Serine  UCG Serine	UAU Tyrosine  UAC Tyrosine  UAA Ochre (Stop)  UAG Amber (Stop)	UGU Cysteine  UGC Cysteine  UGA Opal (Stop)  UGG Tryptophan
	C	CUU Leucine  CUC Leucine  CUA Leucine  CUG Leucine	CCU Proline  CCC Proline  CCA Proline  CCG Proline	CAU Histidine  CAC Histidine  CAA Glutamine  CAG Glutamine	CGU Arginine  CGC Arginine  CGA Arginine  CGG Arginine
	A	AUU Isoleucine  AUC Isoleucine  AUA Isoleucine  AUG Methionine	ACU Threonine  ACC Threonine  ACA Threonine  ACG Threonine	AAU Asparagine  AAC Asparagine  AAA Lysine  AAG Lysine	AGU Serine  AGC Serine  AGA Arginine  AGG Arginine
	G	GUU Valine  GUC Valine  GUA Valine  GUG Valine	GCU Alanine  GCC Alanine  GCA Alanine  GCG Alanine	GAU Aspartic acid  GAC Aspartic acid  GAA Glutamic acid  GAG Glutamic acid	GGU Glycine  GGC Glycine  GGA Glycine  GGG Glycine

Notice that each amino acid is encoded by several codons. In the case of leucine, there are many as six codons. Tryptophan is encoded by only one codon, as is methionine, whose codon is the start codon.

Table 6 lists the 64 base triplets in DNA, the 64 mRNA codons and the 64 tRNA anticodons.

25

---

26

---

Table 6. Table of DNA base triplets, mRNA codons & tRNA anticodons.
(AT or U, CG)

Amino acid	DNA Base Triplets	mRNA Base Codons	tRNA Base Anticodons
alanine	CGA, CGG, CGT, CGC	GCU, GCC, GCA, GCG	CGA, CGG, CGU, CGC
arginine	GCA, GCG, GCT, GCC, TCT, TCC	CGU, CGC, CGA, CGG, AGA, AGG	GCA, GCG, GCU, GCC, UCU, UCC
asparagine	TTA, TTG	AAU, AAC	UUA, UUG
aspartate	CTA, CTG	GAU, GAC	CUA, CUG
cysteine	ACA, ACG	UGA, UGC	ACA, ACG
glutamate	CTT, CTC	GAA, GAG	CUU, CUC
glutamine	GTT, GTC	CAA, CAG	GUU, GUC
glycine	CCA, CCG, CCT, CCC	GGU, GGC, GGA, GGG	CCA, CCG, CCU, CCC
histidine	GTA, GTG	CAU, CAC	GUA, GUG
isoleucine	TAA, TAG, TAT	AUU, AUC, AUA	UAA, UAG, UAU
leucine	AAT, AAC, GAA, GAG, GAT, GAC	UUA, UUG, CUU, CUC, CUA, CUG	AAU, AAC, GAA, GAG, GAU, GAC
lysine	TTT, TTC	AAA, AAG	UUU, UUC
methionine	TAC	AUG	UAC
phenylalanine	AAA, AAG	UUU, UUC	AAA, AAG
proline	GGA, GGG, GGT, GGC	CCU, CCC, CCA, CCG	GGA, GGG, GGU, GGC
serine	AGA, AGG, AGT, AGC, TCA, TCG	UCU, UCC, UCA, UCG, AGU, AGC	AGA, AGG, AGU, AGC, UCA, UCG
stop	ATG, ATT, ACT	UAA, UAG, UGA	AUU, AUC, ACU
threonine	TGA, TGG, TGT, TGC	ACU, ACC, ACA, ACG	UGA, UGG, UGU, UGC
tryptophan	ACC	UGG	ACC
tyrosine	ATA, ATG	UAU, UAC	AUA, AUG
valine	CAA, CAG, CAT, CAC	GUU, GUC, GUA, GUG	CAA, CAG, CAU, CAC

The four bases appear (64×3=192) times in each set of 64 codons. Degeneracy results because a triplet code designates 20 amino acids and a stop codon. Each base appears 48 times. The factorisation of 192 as 48×4 manifests in the inner Tree of Life as the four geometrical elements (corner, outer edge, inner edge & triangle) per sector surrounding the centres of the 48 sectors of each set of seven separate Type A polygons (Fig. 25). Each of four types of geometrical elements appears 48 times in a set and manifests in RNA as one of the four bases C, G, A & U. The elements pair into two boundary elements (corner & edge) and two internal elements (edge & triangle) per sector of a polygon. These two classes correspond to the non-binding pairs (A,C) and (U,G):  

One half of the inner Tree of Life expresses the codons in mRNA and the other half expresses the anticodons in tRNA. The boundary/interior distinction between their geometrical elements corresponds to the complementary nature of the four bases. (For the purpose of illustration, base A has been associated with a corner and base C has been associated with an outer edge. Which is the correct association is an issue that need not detain us here). We showed earlier that the same, 2×64×3 pattern exists in other sacred geometries. For example, the 64 trigrams in one diagonal half of the I Ching table correspond to the 64 mRNA codons and the 64 trigrams in its other half correspond to the 64 tRNA anticodons (Fig. 26). The yin/yang lines denote bases. The yin/yang duality of opposites manifests in the codons as the pair of complementary bases A and U and as the pair of complementary bases C and G. The 64 triplets of yods in each half of the Sri Yantra also represent the 64 codons in RNA and the 64 anticodons in tRNA.

8. The sacred geometry of the codons

Because there are four bases, triplet codons are required to produce at least 21 different codes, that is, codons for the 20 amino acids and at least one stop codon). Doublet codons would produce only (4²=16) different codes. We see that EHYEH, the Godname of Kether with number value 21, determines the three-fold nature of codons. EL, the Godname of Chesed with number value 31, prescribes the 61 codons coding only for the 20 amino acids because 61 is the 31st odd integer. The Decad (10), the

27

---

Pythagorean measure of divine wholeness, determines this important number because the decagon, its geometrical symbol, has 61 yods when its sectors are tetractyses (Fig. 27). Amazingly, the 61st note in the Pythagorean scale, the perfect fifth of the ninth octave, is the 31st harmonic. Moreover, it has a tone ratio of 384 (Fig. 28), which is the very number of times the four nitrogen bases A, C, G & U appear in the 64 mRNA base codons and in the 64 tRNA anticodons! This is not coincidental, for holistic systems exhibit the same set of defining parameters and are 

 

prescribed by Godnames. 64 is the 32nd even integer, where 32 is the 31st integer after 1, showing how EL prescribes the 64 codons. There are 128 possible codons in an mRNA and a tRNA molecule, where 128 is the 127th integer after 1 and 127 is the 31st prime number. EL prescribes the complete codon domain available for life — the number of codons, the number of codons encoding for amino acids and the number of times each base appear in them.

The Pythagorean Tetrad also determines the number 61 because the number 4 is symbolized by a square, the Type B version of which has 61 yods (Fig. 29).

The 64 mRNA codons comprise (3³=27) codons made up of A, C & G bases and (64–27=37) codons containing the U base. Similarly, the 64 tRNA anticodons comprise 37 anticodons containing the A base. Hence, there are 74 such codons and their anticodon counterparts. 74 is the 73rd integer after 1, where 73 is the 21st prime number. The Godname EHYEH with number value 21 prescribes the codons containing the U base and their anticodons. Bases appear in them (3×74=222) times. The pair of separate Type A hexagons of the inner Tree of Life, which we saw earlier correspond to the eight diagonal hexagrams of the I Ching table, contains 74 yods (Fig. 30). As they comprise 50 vertices, edges & triangles, the Godname ELOHIM with number value 50 assigned to Binah in the Tree of Life

28

---

prescribes the geometrical representation of the 37 codons that contain uracil and their anticodons. As 37 is the 36th integer after 1, ELOHA, the Godname of Geburah next below Binah on the Pillar of Judgement with number value 36 prescribes the 37 codons that contain the U base (there are 36 such codons other than the start codon). Of these, three are the stop codons UAA, UAG, UGA. So there are 34 mRNA codons containing the U base that code only for amino acids. They are symbolized by the 34 yods in a pair of joined, Type A triangles (Fig. 31).

A type B triangle has 46 yods (Fig. 32a). 46 is the diploid number for the human cell, namely, its number of chromosomes. The endpoints of the root edge denote the X and Y sex chromosomes. This fundamental information is defined by the Tetrad because two joined, Type A squares have 46 yods (Fig. 32b).

The diploid number of the human cell is embodied in the last polygon itself as the number of hexagonal yods lying on the boundaries of the two joined, Type A dodecagons (Fig. 33). The two hexagonal yods on the root edge denote the two sex chromosomes. A hexagonal yod on the edge of one dodecagon and its counterpart on the other dodecagon symbolize a pair of autosomes.

The Godname ELOHIM prescribes all the codons in human RNA in the following way: the parameter 384 of holistic systems is displayed not only by the complete pair of seven separate Type polygons but also by the two sets of the first six enfolded Type A polygons as their 384 yods other than the endpoints of the root edge (Fig. 34). The 192 yods associated with each set symbolize the 192 instances of the bases in the 64 codons in mRNA and in the 64 codons of tRNA. The 12 polygons symbolizing the 384 instances of all bases constitute a holistic system in themselves

because they are prescribed by the ten Godnames.¹⁷ For example, they have 50 corners, where 50 is the number value of ELOHIM, each set having 26 corners, where 26 is the number value of YAHWEH. Noting that a corner of the triangle is the centre of the hexagon and that a corner of the pentagon is the centre of the decagon, the numbers of yods in each

29

---

enfolded polygon making up the 192 yods associated with each set are:

(the hexagonal yods on the root edge are regarded here as belonging to the pentagons, the corners they share with decagons being counted as belonging to the latter). Associated with each set of the first four enfolded polygons are 90 yods. 36 yods belong to the first two polygons and 54 yods belong to the second pair. This 36:54 division is characteristic of sacred geometries, as well as being arithmetically expressed in the Lambda Tetractys extrapolation of Plato’s Lambda:¹⁸

The clearest illustration of this division in holistic systems is provided by the disdyakis triacontahedron. When its 120 faces and 180 internal triangles formed by its edges are Type A triangles, their 900 sectors comprise (120×3=360) sectors in the faces and (180×3=540) sectors in the interior. Confirmation that the 36:54 division in the yod populations of the first four polygons is an expression of the archetypal pattern of numbers in the Lambda Tetractys is that the individual populations are the sums of the integers in its diagonal rows:

The 192 yods associated with each set of the first six enfolded polygons comprise 90 yods in the first our polygons and 102 yods in the last two polygons. The former has nine corners outside the root edge.

The three stop codons & anticodons
There are (27×3=81) instances of A, C & G bases in the 27 codons that contain only them. There are (37×3=111) instances of the remaining 37 codons that contain at least one U base. These codons comprise the three stop codons UAA, UAG & UGA, which have four instances of A, three instances of U and two instances of G. There are (34×3=102) instances of bases in codons that include the U base and which code solely for amino acids. Hence, the 192 instances of bases consist of 81 instances of A, C & G bases in the 27 codons containing only them, nine instances of bases in the three stop codons and 102 instances of bases in the 34 other codons. Compare this 81:9:102 division with the pattern of yods associated with each set of the six polygons shown in Fig. 34. The 90 yods associated with a set symbolize the 90 instances of either A, C & G bases in the 27 codons or the bases in the stop codons. The 102 yods of the octagon and decagon symbolize the 102 instances of bases in the 34 codons containing a U base. That this is not just a highly improbable coincidence is indicated by the fact that the nine corners consist of the four corners of the hexagon, the two corners of the pentagon and the three corners of the triangle and square — precisely, the numbers of instances of, respectively, A, G & U in

30

---

the three mRNA stop codons (Fig. 35). The same conclusions apply to the 90 yods in the first four polygons enfolded on the other side of the shared root edge. The nine corners that belong solely to this set symbolize the nine instances of the A, C & U bases in the three tRNA stop anticodons AUU, AUC & ACU. The mirror symmetry of the two sets is the geometrical representation of base complementary.

The mRNA start codon AUG, the tRNA start anticodon UAC, the three mRNA stop codons UAG, UGA & UAA and their anticodons AUC, ACU & AUU have nine A, nine U, three G and three C bases. The 60 other codons and the 60 other anticodons have 360 (=36×10) bases (180 per set). The Godname ELOHA with number value 36 prescribes how many instances of the bases occur in mRNA codons and tRNA anticodons other than the start and stop ones. They are made up of 87 A, 87 U, 93 G & 93 C bases. 87 is the number value of Levanah, the Mundane Chakra of Yesod, which is the penultimate Sephirah.

We saw in Section 5 that the disdyakis triacontahedron has 180 edges and 120 faces. With each edge regarded as a double-headed arrow, each half of the Catalan solid has 60 faces with 180 arrows. Compare this with the 60 non-stop/start codons and their 180 bases. The 60 faces in one half of the solid correspond to the 60 mRNA non-stop/start codons and the 60 faces in its inverted half correspond to their 60 tRNA anticodons (Fig. 36). A face and its mirror image are analogous to an mRNA codon and its anticodon in tRNA. Their counterparts in the inner Tree of Life

are the 120 yods on the sides of the seven enfolded polygons (Fig. 37). The 60 red yods in the triangle, square, pentagon & dodecagon symbolize the 60 mRNA codons and the 60 blue yods in the hexagon, octagon & decagon denote their 60 anticodons in tRNA. The 180 arrows in one half of the disdyakis triacontahedron correspond to the 180 bases in the 60 mRNA codons and the 180 arrows in the other half correspond to the 180 bases in the 60 tRNA anticodons. The surface of the disdyakis triacontahedron is a geometrical representation of all the instances of the bases that occur in mRNA & tRNA that do not initiate or stop translation. The 24 bases making up the four mRNA start/stop codons and their anticodons in tRNA are represented by the 24 arrows on the internal edges of the sectors of the central, 12-sided polygon, nine arrows and their reverses symbolizing the pair of complementary bases A & U and three arrows and their reverses symbolizing the pair of complementary bases C & G:

(×9): AU                  (×3): CG

Twelve inward-pointing arrows denote either the nine A and three C bases or the nine U and three G bases. The twelve outward pointing arrows denote, respectively, either the nine U and three G bases

31

---

or the nine A and three C bases. The bi-directionality of an arrow expresses the complementary nature of bases whereby they bind in pairs, so that a given double-headed arrow denotes a base and its complement. This correlation between the geometry of the disdyakis triacontahedron and the distinction between codons and anticodons that start or stop translation is highly evidential because, although there should be equal numbers (n) of A & U and equal numbers (12–n) of C & G in them, there is no a priori reason why n should be a multiple of 3 so as to match the three types of internal edges ending on A, B & C vertices. The geometry of the polyhedron is consistent with scientific facts about the base composition of the start and stop codons.

The two Type A dodecagons of the inner Tree of Life encode the 60 codons and 60 anticodons because each has 60 hexagonal yods (Fig. 38a). The 180 yods surrounding the centre of each Type B dodecagon encode the 180 instances of their bases (Fig. 38b). They can be grouped into 60 triplets of red, green & blue yods. The yod composition of the pair of dodecagons is consistent with the codon structure of mRNA and tRNA.

9. The 7-tree encodes the 384 instances of the bases

The Tree of Life is the template for representing holistic systems. The so-called ‘n-tree’ is defined as the lowest n Trees of Life of any set of overlapping Trees of Life. When the (12n+7) triangles in the n-tree are converted into tetractyses, they have¹⁹

Y(n) = 50n + 30

yods. The 7-tree has Y(7) = 380 yods. The 7-tree is but part of the 91 overlapping Trees of Life of the Cosmic Tree of Life (CTOL). Figure 39 shows that four yods belonging to the eighth Tree of Life lie outside the 7-tree (two on each side of the central Pillar of Equilibrium). There are therefore 384 yods up

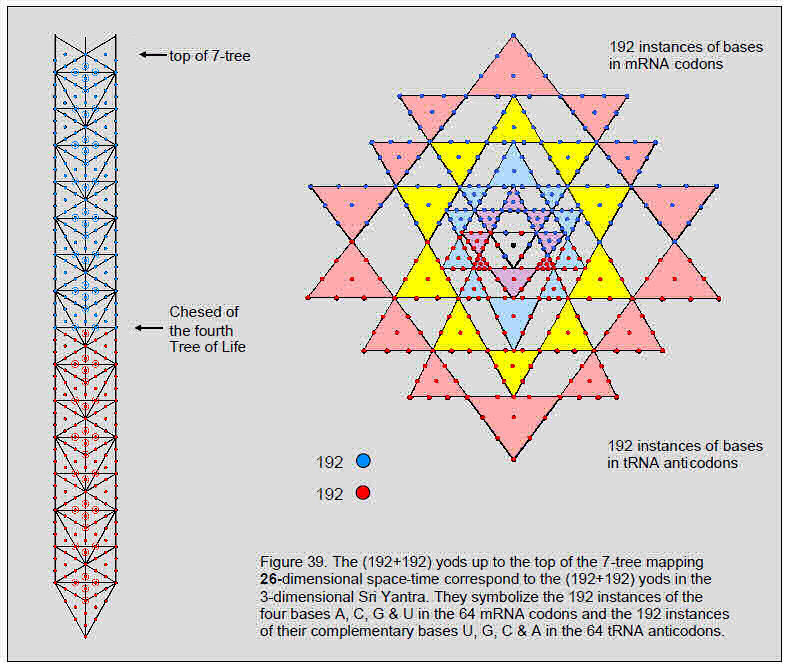
32

---

to the apex of the 7-tree. In previous articles, the 7-tree has been interpreted as mapping the 26-dimensional space-time predicted by string theory. It maps the purely physical level of the spiritual cosmos. We find therefore that the number 384 characterizes the Tree of Life representation of the physical universe. The number of yods below Chesed of the nth Tree of Life is²⁰

Y'(n) = 50n – 8.

Hence Y'(4) = 192. The 384 yods as far as the top of the 7-tree divides into 192 yods below Chesed of the fourth Tree of Life (denoted in Fig. 39) by red yods) and 192 blue yods down to this point. They are the counterpart of the 192 yods in each half of the Sri Yantra. The former symbolize the 192 instances of the bases in the mRNA codons and the latter symbolize the 192 instances of the bases in the tRNA anticodons. The two halves of the 7-tree, the inner Tree of Life and the Sri Yantra represent the mRNA and the tRNA molecules. It is the molecular

manifestation of the fundamental yin and yang polarities in nature, as manifested in the electrostatic attraction between the positively charged proton of the hydrogen atom in the nitrogen bases and the electrons in the nitrogen and oxygen atoms of their complementary bases (see Fig. 23).

The 192 red yods belong to 46 triangles with 23 vertices & 62 edges, i.e., 131 geometrical elements. 131 is the number value of Samael, the Archangel of Geburah. 62 is the number value of Tzadkiel, the Archangel of Chesed, which is the Sephirah preceding Geburah. 131 is the 65th odd integer after 1. Hence, ADONAI, the Godname of Malkuth with number value 65, prescribes the geometry whose 192 yods symbolize the 192 instances of the bases of the 64 tRNA anticodons. The 384 red & blue yods belong to 93 triangles with 47 vertices & 123 edges, i.e., 263 

geometrical elements. 47 is the 15th prime number. Hence, YAH, Godname of Chokmah with number value 15, prescribes the 7-tree embodying as yods the 384 instances of the bases in the 64 codons of mRNA and the 64 anticodons of tRNA. YAH prescribes the 7-tree also because it has 15 SLs on each side pillar. There are 216 edges & triangles, where 216 is the number value of Geburah. Each set of 192 yods belong to sections with 85

33

---

vertices & edges, where

85 = 4⁰ + 4¹ + 4² + 4³

is a parameter of holistic systems because it is the number of yods in the next higher differentiation of the tetractys (1st-order tetractys), namely, the 2nd-order tetractys (Fig. 40). The Tetrad (4) expresses the properties of holistic systems. Its symbol — the square — has 25 yods when it is Type A (see Fig. 32). It is the polygonal counterpart of the 25 SLs up to Chesed of the fourth Tree of Life that divides the 384 yods up to the top of the seventh Tree of Life into two sets of 192 yods.

The Tree of Life basis of the pattern of 64 codons and 64 anticodons can be demonstrated as follows: if each Sephirah is replaced by a Tree of Life, the resulting ten Trees of Life (Fig. 41) have 64 ‘Sephirothic levels’ (SLs). This is how the number 64 parameterizes the next higher order differentiation of the Tree of Life. They comprise Kether, Chokmah & Binah of the tenth Tree of Life and 61 SLs, starting with Chesed of that Tree of Life. They correspond, respectively, to the three stop codons and the 61 other codons. The matching demonstrates the Tree of Life basis of the DNA/RNA molecule. Below this Supernal Triad are 20 SLs on each side pillar. It is an indication that there are 20 amino acids coded by at least 20 codons.

Now suppose that each of the 64 SLs is replaced by a Tree of Life. There are then 64 overlapping Trees of Life and 385 SLs up to Chesed of the 64th one, where

385 =

12 22 32 42 52 62     72 82 92 102 .

This shows beautifully how the Decad determines the 384 SLs needed to emanate the 64 Trees of Life, starting from the first Sephirah of Construction of the highest one, before reaching the nadir at Malkuth of the first one. They are arranged in 32 pairs of triads in the uppermost 32 Trees of Life and in 32 pairs of triads in the lowest 32 Trees of Life. The former set corresponds to the 32 mRNA codons (a,b,c) (a, b, c = A, U, C & G) and their 32 complements (a*,b*,c*), where a* is complementary to a, b* is complementary to b and c* is complementary to c. The latter set

corresponds to the 32 tRNA anticodons (a*,b*,c*) and their complements (a,b,c). In other words, the two triads of Sephiroth of Construction within each Tree of Life in the uppermost 32 Trees of Life denote a codon and its complement in mRNA, whilst in the lowest 32 Trees of Life they denote a codon and its complement in tRNA. These two sets of 64 triads of SLs are the counterpart of the 64 trigrams in each half of the I Ching table, which represent mRNA and tRNA. The 64 triads of SLs in each set of 32 Trees of Life have their counterpart also in the 192 edges & triangles belonging to S and the 192 edges & triangles belonging to S', discussed in Section 1. The triangle and pentagon have 64 edges & triangles, whilst the square and dodecagon have twice as many. The counterpart of the former in the 64 triads of SLs in the upper 32 Trees of Life are the 64 SLs on the central pillar; the counterpart of the latter are the 64 pairs of SLs on the side pillars. For S', the octagon, which has the same number of sectors as the triangle & pentagon, possesses 64 edges & triangles, whilst the hexagon & decagon, which has the same number of sectors as the square & dodecagon, has twice as many. The counterpart of the former in the 64 triads in the lower set of 32 Trees of Life are the 64 SLs on the central pillar; the counterpart of the latter are the 64 pairs of SLs on the side pillars. The fact that the 192 edges & triangles are divided into three groups reflects the fact that the Sephiroth are arranged on three pillars. The analogy between the 64 codons and the geometry of the inner Tree of Life implies that the triple nature of codons is a direct reflection of the three pillars of the outer Tree of Life. This is not a metaphysical speculation. Instead, it is a mathematical deduction from this analogy.

34

---

It is appropriate that Nogah, the Mundane Chakra of Netzach, which is the Sephirah that expresses the richness and variety of biological species, should have the gematria number value 64 (see Table 1). It is the number of corners (red yods) of the two sets of seven enfolded polygons that do not coincide with Sephiroth, for Figure 42 shows that the former have 70 corners, of which three corners (white yods) of the hexagon in one set coincide with Chokmah, Chesed & Netzach and of which three corners (also white yods) of the hexagon in the other set coincide with Binah, Geburah & Hod. The endpoints of their shared root edge do not coincide with Tiphareth and Daath because the latter do not lie in the plane of the two side pillars of the 3-dimensional Tree of Life. The 64 corners (32 in each set of polygons) that the inner Tree of Life does not share with its outer form represent new degrees of freedom characterizing any system that embodies this universal paradigm. Similarly, the outer form of the Tree of Life has 70 yods, when its 16 triangles turn into tetractyses, so that it, too, has 64 black yods unshared with its inner form. We may regard the 64 unshared corners of the latter as the representation of the 64 types of codons of mRNA that can potentially bind to their corresponding anticodons in tRNA symbolized by the 64 yods in the outer Tree of Life. The conjoined geometries of the inner and outer forms of the Tree of Life embody the very fundamental numbers involved in the replication of the DNA molecule. The 20 corners outside the shared root edge of the pair of dodecagons (the last polygon) symbolize the minimum number of codons that encode for amino acids. The inner TOL predicts how many amino acids exist. Their counterpart anticodons in the outer Tree of Life are the 20 yods making up the tetrahedron, which is the last stage in the sequence:

point → line → triangle → tetrahedron

that collectively constitutes its trunk. This was shown in Article 33 to represent the 80 bones of the axial skeleton.²¹ We saw earlier in Fig. 33 that the 46 hexagonal yods lying on the boundary of the two dodecagons symbolize the 46 chromosomes in the human cell.

Three of the 64 mRNA codons — the stop codons — are special in that they do not encode for amino acids. If the 64 corners of the polygons unshared with the Tree of Life really do symbolize codons, then there must be three of them that differ from the rest in some way. One corner of the pentagon coincides with the centre of the decagon and the lower endpoint of the root edge is the only one of the 64 unshared corners that coincides with the projection of the locations of Sephiroth onto the plane of the 14 polygons. Hence, there are three corners that are different from the rest. Admittedly, they have not been independently proven to symbolize these codons. But the criticism that interpreting them this way is ad hoc misses the point. What is being pointed out here is simply that (as one would expect) the sacred geometry of the inner TOL naturally exhibits a distinction between three of the corners and the other 61 that mirrors the difference between the stop codons and the codons that encode only for amino acids. Whether these three corners do symbolize the stop codons still has to proved, although, intuitively speaking, it is appropriate that the lower endpoint of the root edge, which marks the completion of the generation of the 14 polygons, should denote a stop codon. It is also intuitively appropriate that the start codon should be identified with the upper endpoint of the root edge, which is the starting point for the generation of the inner TOL. The counterparts in the outer Tree of Life of the three corners denoting the stop codons in mRNA are the yods at Tiphareth, Yesod & Malkuth, which symbolize the three stop anticodons in tRNA. Appropriately, the yod at Kether denotes the start anticodon in tRNA. The counterpart of the three stop codons in the ten overlapping Trees of Life with 64 SLs shown in Figure 38 are Kether, Chokmah & Binah of the tenth Tree of Life, the remaining 61 SLs corresponding to the 61 codons. The fact that there are 20 SLs on each side pillar reflects the fact that there must be a minimum of 20 codons that encode for the 20 amino acids. The start codon AUG would correspond to the first of these 61 SLs, namely, Chesed of the tenth Tree of Life.

It is remarkable that there are 128 vertices, edges & faces of the first four Platonic solids, which were believed by the ancient Greeks to be the shapes of the particles of the Elements Earth, Water, Air & Fire:

	vertices	edges	faces	Total
tetrahedron	2+2	3+3	2+2	7+7 =  14
octahedron	3+3	6+6	4+4	13+13 =  26
cube	4+4	6+6	3+3	13+13 =  26
icosahedron	6+6	15+15	10+10	31+31 =  62
Total =	15+15	30+30	19+19	64+64 = 128

The 64 mRNA codons correspond to the 64 geometrical elements in half of the four polyhedra and their counterpart 64 anticodons in tRNA correspond to the 64 elements in their other halves. It is evidence that the pattern of codons in human DNA is not merely a product of random, evolutionary change over millions of years. Instead, it is a manifestation of sacred geometries that embody the divine archetypes. Each half

35

---

Table 7. DNA-type patterns of equivalence in representations of holistic systems.

(7+7) separate Type A polygons	7 Type B polygons	I Ching table	Sri Yantra	7 musical scales	disdyakis triacontahedron	mRNA & tRNA
384 vertices, edges & triangles surround centres of two sets of 7 polygons	384 edges & triangles	384 lines & broken lines	384 yods in 43 triangles	384 intervals between notes	384 double-headed arrows along edges	384 instances of 4 bases
192 vertices, edges & triangles surround centres of 7 polygons in each set	192 edges & triangles in triangle, square, pentagon & dodecagon or in hexagon, octagon & decagon	192 lines & broken lines in each diagonal half	192 yods in each half	192 rising or falling intervals	192 double-headed arrows on edges in each half	192 instances of 4 bases in mRNA or tRNA
128 triplets of geometrical elements surround centres of 14 polygons	128 triplets of edges & triangles	128 trigrams	128 triplets of yods	128 triplets of rising/falling intervals	128 triads of arrows	128 codons/anticodons
64 triplets of geometrical elements surround centres of 7 polygons in one set	64 triplets of edges & triangles in triangle, square, pentagon & dodecagon (S)	64 trigrams in upper, diagonal half	64 triplets of yods in upper half	64 triplets of rising intervals	64 triads of arrows in one half	64 codons
64 triplets of geometrical elements surround centres of 7 polygons in other set	64 triplets of edges & triangles hexagon, octagon & decagon (S')	64 trigrams in lower, diagonal half	64 triplets of yods in lower half	64 triplets of falling intervals	64 triads of arrows in other half	64 anticodons
64×3 geometrical elements in each set of 7 polygons	64 triplets of edges & triangles in either S or S'	64×3 lines & broken lines in each half	64 triplets of yods in each half	64×3 rising/falling intervals	64×3 arrows in each half	64×3 bases
A boundary and an internal geometrical element	Geometrical element and its diametric opposite	Line (yang) and broken line (yin)	Corresponding yods in each half	Rising & falling intervals	An arrow and its reverse	A base & its complement

36

---

comprises (15+19=34) vertices & faces and 30 edges. We pointed out earlier that the 64 mRNA codons comprise 27 codons made up of A, C & G bases and 37 codons containing the U base, 34 of which are non-stop codons. This 27:34 division of codons that encode only for amino acids manifests in the first four Platonic solids as the 27 edges of the octahedron, cube & icosahedron and as the 34 vertices & faces of all four solids. It means that the six edges of the tetrahedron must correspond to the three stop codons of mRNA and the three stop anticodons of tRNA (they cannot correspond to either the six vertices of the octahedron or to the six faces of the cube because this would not generate the numbers 27 & 34). The 27 remaining edges in each half correspond either to the 27 codons or to their 27 anticodons made up of, respectively, A, C & G or U, G & C bases. The 34 vertices & faces in each half correspond to the 34 nonstop codons in mRNA that contain at least one U base and their anticodon counterparts.

The tetrahedron, octahedron, cube & icosahedron embody the number 128 because — as the first four regular polyhedra associated with the Elements of Earth, Water, Air & Fire — they constitute a holistic system that is prescribed by the Godnames.²² For example, the Godname YAH (YH) with number value 15 prescribes the 15 vertices in each half of the solids, the value 5 of H being the number of vertices in each half of the tetrahedron and octahedron and the value 10 of Y being the number of vertices in each half of the cube and icosahedron. The number value 49 of the Godname EL ChAI is the number of edges & faces in half of these solids. The number value 31 of EL is the number of geometrical elements in the icosahedron and the number value 21 of EHYEH is the number of its vertices & edges. The number value 26 of YAHWEH is the number of elements in the octahedron, as well as the cube. When their faces are divided into their sectors, the four solids have 120 triangles with 248 corners & sides.²³ This shows how they embody the dimension 248 of the superstring gauge symmetry group E₈. It is the number value of Raziel, the Archangel of Chokmah (Table 1).

The number 128 is the sum of the number values of the first four Godnames (see Table 1):

128 = 21 + 26 + 50 + 31.

As many previous articles have demonstrated, the Pythagorean Tetrad determines and expresses all parameters of holistic systems, such as 64 (=4³) and 128. As Fig. 29 shows, its symbol — the square — possesses 61 yods, when its sectors are Type A triangles. They symbolize the 61 codons encoding only for the amino acids. Surrounding its centre are 20 yods on its edges & diagonals. This expresses the fact that there has to be at least 20 codons with this function. A Type A square also embodies this information as its 20 hexagonal yods. The fourth Godname, EL (“God”), which has the number value 31, prescribes the 61 non-stop codons because 61 is the 31st odd integer, whilst 128 (the sum of the first four Godname numbers) is the 127th integer after 1, where 127 is the 31st prime number. Such arithmetic connections cannot arise by coincidence. Instead, they indicate that numbers characterizing the human DNA molecule are prescribed by Godnames because man ultimately has a divine origin that is indicated by the way in which this articles has proved the architecture of his DNA molecule conforms to sacred geometries found in Judaism, Taoism and Hindu Tantra.

Table 7 lists equivalent features of the (7+7) separate Type A polygons, the seven separate Type B polygons, the I Ching table, the Sri Yantra, the seven musical scales, the disdyakis triacontahedron and the RNA codons & anticodons.

References & notes

¹ All numbers from this table mentioned in the text will be written in boldface.

² Phillips, Stephen M. Article 4: “Godnames prescribe inner Tree of Life,” (WEB, PDF), pp. 1–2.

³ Ibid.

⁴ Phillips, Stephen M. Article 3: “The sacred geometry of the Platonic solids,” (WEB, PDF), pp. 9, 20.

⁵ Ibid., p. 10.

⁶ Phillips, Stephen M. Article 40: “The unification of all sacred geometries and its implication for particle physics,” (WEB, PDF), pp. 23-26.

⁷ Phillips, Stephen M. Article 20: “Algebraic, arithmetic & geometric interpretations of the I Ching table;” Article 21: “Isomorphism between the I Ching table, the 3×3×3 array of cubes and the Klein Configuration,” (WEB, PDF).

⁸ Phillips, Stephen M. Article 26: “How the seven musical scales relate to the disdyakis

37

---

triacontahedron,” (WEB, PDF), p. 13.

⁹ Phillips, Stephen M. Article 39: “The correspondence between the inner Tree of Life, the Sri Yantra & the I Ching diagram and their realization in the seven musical scales,” (WEB, PDF), p. 4.

¹⁰ Phillips, Stephen M. Article 35: “The Tree of Life nature of the Sri Yantra and some of its scientific meanings,” (WEB, PDF).

¹¹ Phillips, Stephen M. Article 22: “The disdyakis triacontahedron as the 3-dimensional counterpart of the inner Tree of Life,” (WEB, PDF).

¹² Phillips, Stephen M. Article 23: “The Polyhedral Tree of Life,” (WEB, PDF).

¹³ Phillips, Stephen M. Article 24: “More evidence for the disdyakis triacontahedron as the 3-dimensional realisation of the inner Tree of Life and its manifestation in the E₈×E₈ heterotic superstring,” (WEB, PDF).

¹⁴ A triangular prism is two similarly orientated, parallel, identical triangles with a straight edge joining their corresponding vertices. A square antiprism is two similar, parallel squares orientated at an angle of 45° with two edges of the antiprism joining each corner of one square to the two nearest corners of the other square.

¹⁵ Phillips, Stephen M. Article 43: “The Tree of Life nature of the {3,7} tessellation of the 168 automorphisms of the Klein quartic on the 3-torus,” (WEB, PDF).

¹⁶ There are other amino acids, such as selenocysteine. However, it is not coded for directly in the genetic code. Instead, it is encoded in a special way by a UGA codon, which is normally a stop codon.

¹⁷ Ref. 2, pp. 4–5.

¹⁸ Phillips, Stephen M. Article 11: “Plato’s Lambda — its meaning, generalisation and connection to the Tree of Life,” (WEB, PDF).

¹⁹ Proof: the n-tree has (12n+7) triangles with (6n+5) corners and (16n+9) edges. Two hexagonal yods lie along each edge and one hexagonal yod is at the centre of each triangle when it becomes a triangle. The number of yods in the n-tree ≡ Y(n) = 6n + 5 + 2(16n+9) + 12n + 7 = 50n + 30.

²⁰ Proof: there are 12 yods below Chesed of the nth Tree of Life that are outside the (n–1)-tree. The number of yods in the latter is Y(n–1) = 50(n–1) + 30 = 50n – 20. Therefore, the number of yods below Chesed of the nth Tree of Life ≡ Y'(n) = 50n – 20 + 12 = 50n – 8.

²¹ Phillips, Stephen M. Article 33: “The human axial skeleton is the trunk of the Tree of Life,” (WEB, PDF).

²² Ref. 4, pp. 9–10.

²³ Ref. 4, p. 10.

Information embedded in DNA proves the existence of God

 

 

 

38