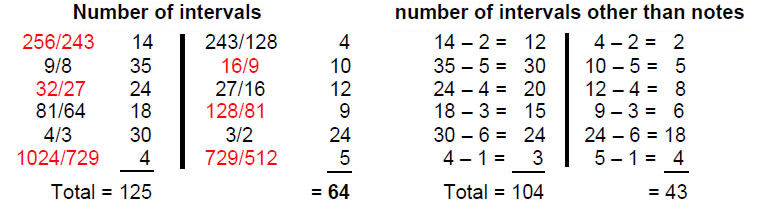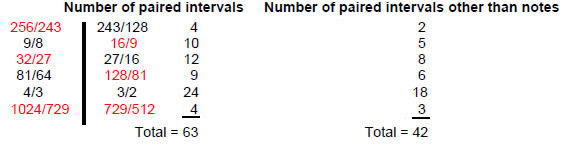ARTICLE 39
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.Website: http://smphillips.mysite.com
Abstract
|
The seven possible types of musical scale have 137 Pythagorean intervals when their tonics and octaves are included. 137 is the nearest integer value of the reciprocal of the fine-structure constant playing a central role in atomic physics. 46 of them other than tonics and octaves appear in sets of different intervals in each scale. There are 84 repetitions of the intervals in these sets. The 189 intervals in the seven scales consist of 125 intervals with tone ratios up to 1024/729 and 64 of their complements. Of these, 63 intervals can be paired with their complements, leaving 63 unmatched intervals or complements. The 189 intervals therefore form three distinct groups: 63 intervals, 63 matched complements and 63 unmatched intervals or complements. To each rising interval there corresponds a falling interval with a tone ratio that is the reciprocal of that of the former. The 378 rising and falling intervals comprise 63 pairs of triplets of intervals. There is also the tonic with tone ratio 1, the rising interval 1, the falling interval 1, the octave 2 as a note, the rising octave interval of 2 and the falling octave interval of ½. The 64 pairs of triplets of intervals are symbolized in the I Ching table as the 64 pairs of trigrams. Of the 63 intervals, 21 are the second, third and fourth notes of each scale. There are 42 rising and falling note intervals symbolized by the 42 Yang/Yin lines of the seven hexagrams in the diagonal of the 8×8 square array of hexagrams below the pair of Heaven trigrams at the top left-hand corner of the array. This pair of three Yang lines symbolizes the three types of unit intervals and the three types of octave intervals. In the Sri Yantra, the 378 rising and falling intervals in the seven scales correspond to the 378 yods of its 42 triangles. The six lines of the pair of Heaven trigrams have their counterpart in the six hexagonal yods of its central triangle, whilst the 42 hexagonal yods at the centres of the 42 triangles correspond to the 42 Yang/Yin lines of the seven other hexagrams on the diagonal of the table. The (168+168) Yang/Yin lines in the (28+28) hexagrams on either side of the diagonal of the I Ching table correspond to the (168+168) yods on the edges of the 42 triangles. They symbolize the 168 rising and falling intervals that are not notes and the 168 rising and falling, unpaired intervals or complements of the 21 notes. They correspond in the Sri Yantra to the (168+168) yods on the edges of its 42 triangles. |
1
1. The interval composition of the seven musical scales.
It was proved in Article 38 that the 14 types of notes making up the seven musical scales have 91 intervals, among which are 24 pairs of intervals and their complements. They correspond in the inner form of the Tree of Life to the 24 pairs of vertices of the two sets of six enfolded, regular polygons outside their shared, root edge, the endpoints of which denote the tonic and octave. It is shown here that the notes of the seven scales have 189 intervals, among which there is an analogous set of 24 pairs of perfect fourths and perfect fifths.Tables 6–12 show the tone ratios of the intervals in each scale. Turquoise cells contain different, rising intervals. Yellow cells contain repetitions of these intervals. White cells represent falling intervals. Their inverted tone ratios are omitted for the sake of clarity. Black tone ratios are those of the Pythagorean (C) scale. Red tone ratios are non-Pythagorean. P = Pythagorean interval; NP = non-Pythagorean interval.
C D E F G A B C 1 Number of P = 20.
Number of NP = 8.
Number of different intervals
= 7 (P) + 5 (NP) = 12.
Number of repeated intervals
= 13 (P) + 3 (NP) = 16.
C
D
E
F
G
A
B
C
C D E F G A B C Number of P = 18.
Number of NP = 10.
Number of different intervals
= 6 (P) + 5 (NP) = 11.
Number of repeated intervals
= 12 (P) + 5 (NP) = 17.
C
D
E
F
G
A
B
C
C D E F G A B C Number of P = 20.
Number of NP = 8.
Number of different intervals
= 7 (P) + 5 (NP) = 12.
Number of repeated intervals
= 13 (P) + 3 (NP) = 16.
2
C
D
E
F
G
A
B
C C D E F G A B C Number of P = 19.
Number of NP = 9.
Number of different intervals
= 7 (P) + 6 (NP) = 13.
Number of repeated intervals
= 12 (P) + 3 (NP) = 15.
C
D
E
F
G
A
B
C
C D E F G A B C Number of P = 17.
Number of NP = 11.
Number of different intervals
= 6 (P) + 5 (NP) = 11.
Number of repeated intervals
= 11 (P) + 6 (NP) = 17.
C D E F G A B C C D E F G A B C Number of P = 17.
Number of NP = 11.
Number of different intervals
= 6 (P) + 5 (NP) = 11.
Number of repeated intervals
= 11 (P) + 6 (NP) = 17.
C
D
E
F
G
A
B
C
C D E F G A B C Number of P = 19.
Number of NP = 9.
Number of different intervals
= 7 (P) + 6 (NP) = 13.
Number of repeated intervals
= 12 (P) + 3 (NP) = 15.
3
The 196 rising intervals between the 56 notes in the seven types of musical scales comprise 130 Pythagorean intervals and 66 non-Pythagorean intervals. This demonstrates how the Godname ADONAI with number value 651 prescribes the seven scales, for 130 is the 65th even integer and 66 is the 65th integer after 1. The Godname YAHWEH SABAOTH with number value 129 prescribes them because 130 is the 129th integer after 1. Including the tonics 1 of each scale (formally a Pythagorean note because it occurs in the Pythagorean scale), there are 137 Pythagorean intervals. Remarkably, the number 137, which is one of the most important numbers in physics because it defines the reciprocal of the fine-structure constant measuring the strength of the coupling of the electron to the electromagnetic field, is simply the total number of notes and their intervals in the seven scales that are notes of the Pythagorean scale!
Each scale has a minimum number of basic intervals (indicated in the tables as turquoise cells), most of which are repeated (yellow cells). Their numbers are indicated in the text accompanying the tables shown above. All seven scales have 83 of them (46 Pythagorean, 37 non-Pythagorean). Including the tonics, there are (46+7=53) Pythagorean intervals distributed among these minimal sets, that is, (53+37=90) intervals in total. This illustrates the power of Plato’s Lambda Tetractys to define the properties of holistic systems, for the 14 different types of notes making up the seven musical scales have 90 intervals below the octave and 90 is the sum of the 10 integers in this tetractys. Excluding the tonics and octaves, there are in the seven scales (46–7=39) Pythagorean intervals and 37 non-Pythagorean intervals (76 intervals) that are repeated. This shows how the Godname YAHWEH ELOHIM with number value 76 prescribes the core intervals in the musical scales.
There are (196–83=113) repetitions of the sets of different notes in each scale. (130–46=84) of these repeated intervals are Pythagorean:
Total = 84.
This number appeared in Article 38’s analysis of the 90 intervals between the 14 different notes of the seven scales as the 84 intervals other than the six perfect fifths.
Tabulated below are the numbers of intervals of each type other than the octave and the numbers that are not notes.
The 189 intervals (123 Pythagorean, 66 non-Pythagorean) comprise 125 intervals (83 Pythagorean, 42 non-Pythagorean) and 64 of their complements (40 Pythagorean, 24 non-Pythagorean). Of these, 21 (14 Pythagorean, 7 non-Pythagorean) are notes and 21 (12 Pythagorean, 9 non-Pythagorean) are their complements, i.e., the 42 notes of the seven scales comprise (14+12=26) Pythagorean notes and (7+9=16) non-Pythagorean notes. This shows how the Godname YAHWEH with number value 26 prescribes the 26 Pythagorean notes in the seven scales and how the Godname EHYEH with number
4
value 21 prescribes the 21 notes between the tonic and octave and their 21 complements.
If we include the octaves of each scale, there are (189+7=196) rising intervals. The number 196 is the mean distance, measured in units of 1/10 AU, of the planet Uranus from the Sun predicted by the Titius-Bode Law.2 The number 7 is the distance of the planet Venus from the Sun predicted by the law. Hence, the number 189 measures the distance between Venus and Uranus.
This is not coincidental, according to the theory of the Solar System presented in Article 17, for it regards the eight planets up to Uranus as members of an octet (analogous to a musical octave) whose orbital mean distances were determined by that of Mercury, which acts as the tonic of this planetary octave.
5
Some of the 189 intervals can be paired with their complement. Tabulated below are the number of such pairs for each type of interval and the number of pairs that are not notes in the seven scales:
There are at most 63 intervals other than the tonic and octave of each scale that can be paired with their corresponding complements. This leaves 63 intervals unpaired. They consist of 83 Pythagorean intervals and 43 non-Pythagorean intervals. Just as there are 63 pairs of intervals and their complements, so there are 63 pairs of bones in the human appendicular skeleton, one bone located on the right-hand side of the skeleton, the other on the left-hand side.3 The analogy can be made that tonal complementarity corresponds to the left/right mirror symmetry of the human body. It expresses balance.
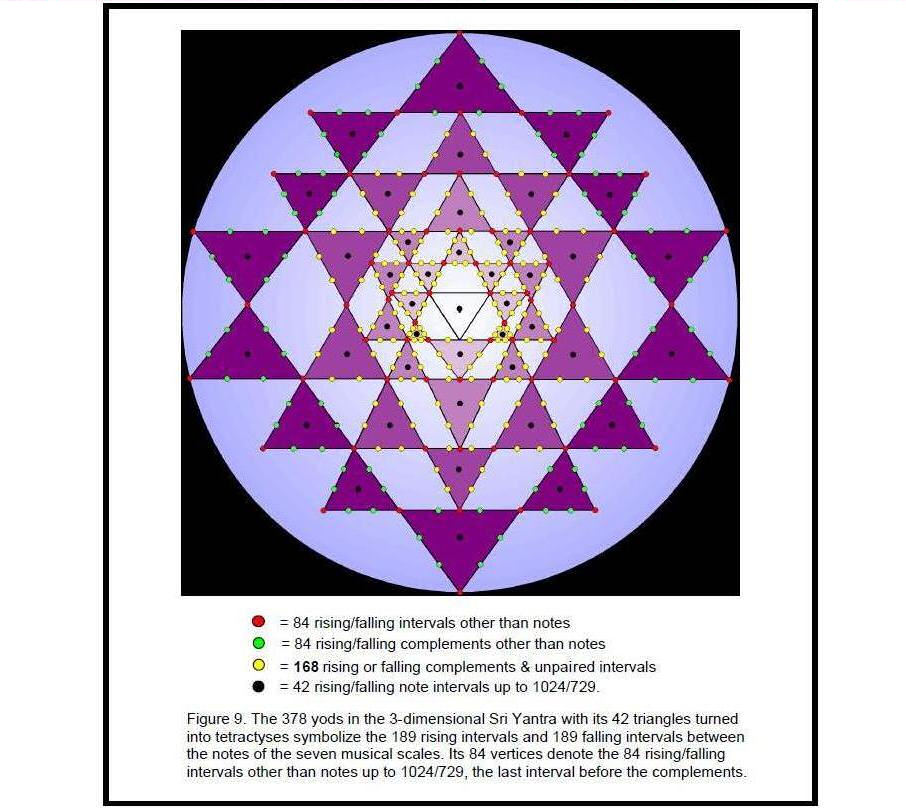
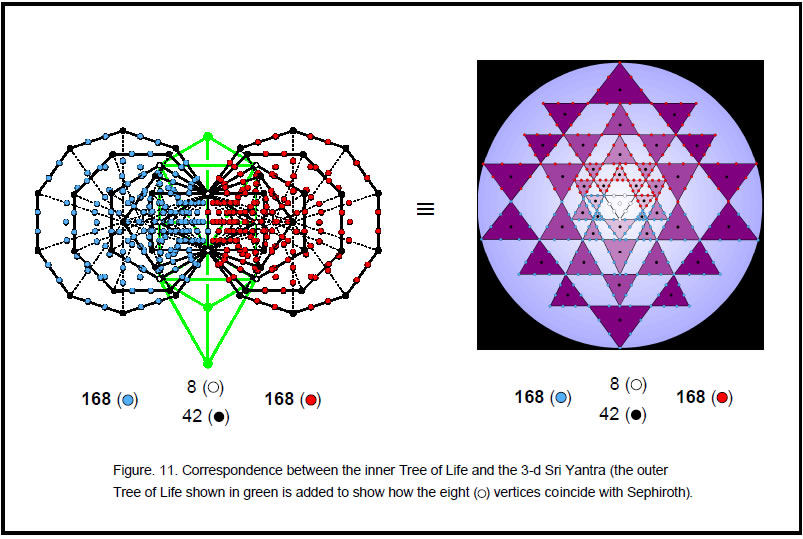
The seven scales have 189 rising intervals other than octaves and 189 falling intervals, that is, 378 rising and falling intervals. This is the number of yods making up the 42 triangles of the 3-d Sri Yantra when they are turned into tetractyses.4 That this is no coincidence is indicated by the fact that the maximum number of pairs of intervals and their complements that be selected from the 189 intervals is 63 (see above), leaving 63 unpaired intervals, so that there are 126 rising and falling unpaired intervals and 252 rising and falling paired intervals, which could correspond, respectively, to the 126 yods either on the edges of the fourth layer of triangles or at the centres of all 42 triangles and to the 252 yods either on edges of the first three layers of triangles or at their
vertices (Fig. 9).5 It is tempting to associate the 42 notes between the tonic and octave
6
7
of the seven scales and their 42 falling intervals with the 84 vertices of the 42 triangles in the 3-d Sri Yantra that surround its central one. However, this identification is incorrect because it is inconsistent with the correlation between the Sri Yantra and the inner Tree of Life (see below), in which the 42 yods at centres of triangles in the former correspond to the 42 corners of polygons symbolizing tone ratios of notes and their reciprocals, which means that vertices of triangles cannot denote notes. Here is the breakdown of the interval composition of the seven scales that enables an unambiguous identification to be made:
189 intervals = 63 pairs of intervals & their complements + 63 unpaired intervals
= 42 pairs of intervals other than notes + 21 pairs of notes + 63 unpaired intervals
= 42 intervals & 42 complements + 21 notes & 21 complements + 63 unpaired intervals.
378 rising/falling intervals = 84 rising/falling intervals other than notes + their 84 rising/falling complements + 42 rising/falling note intervals + (42 rising/falling complements + 126 rising/falling, unpaired intervals)
84 vertices + 84 hexagonal yods on edges of triangles in 4th layer + 42 yods at centres of 42 triangles + (42+126=168) hexagonal yods on edges of triangles in first 3 layers.
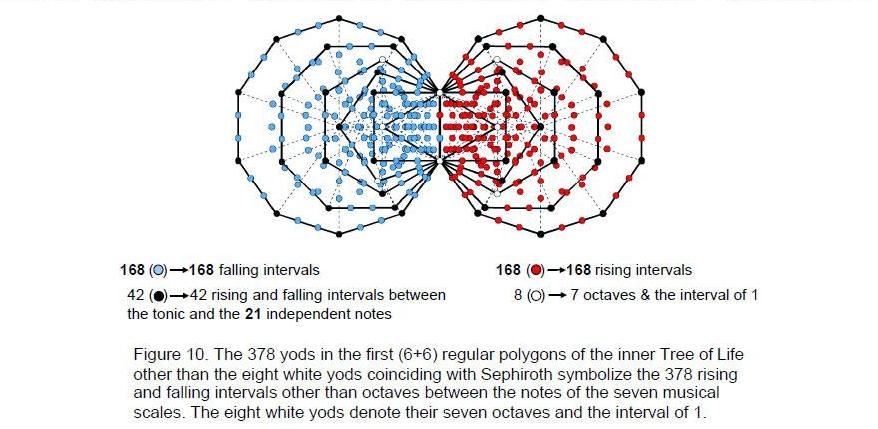
This correlation demonstrates the meaning of the Sri Yantra as a representation of holistic systems such as the seven kinds of musical scales. Its 84 vertices denote the 84 rising and falling intervals other than notes up to that with tone ratio 1024/729, the largest of the independent intervals (independent in the sense that the larger intervals are their complements and are thus determined by them). The yods at the centres of the 42 triangles denote the 42 rising/falling note intervals up to 1024/729.Being an analogous blueprint, the inner Tree of Life encodes the 378 intervals as well. The first (6+6) enfolded polygons have 386 yods (Fig. 10). Of these, the eight white yods coincide with Sephiroth or Daath, leaving 378 yods. The 189 yods associated with one set of polygons denote the 189 rising intervals and the 189 yods associated with its mirror image set of polygons denote the 189 falling intervals. The 42 vertices of the 12 polygons not shared with the outer Tree of Life denote the rising and falling intervals of the 21 independent notes with tone ratios up to 1024/729. The eight shared, white yods denote the seven octaves and the interval of 1. The 336 yods other than vertices denote rising and falling intervals between notes and correspond to the 336 yods lying along the 126 edges of the 42 triangles of the Sri Yantra.6 The 42 vertices not coinciding with Sephiroth correspond to the 42 yods at the centres of the 42 triangles. The (1+7) white yods (“1” denotes Daath) and the three remaining Sephiroth of the Tree of Life correspond to the bindu point and the (7+3) yods of the central triangle. The remarkable correspondence between the Sri Yantra and the inner Tree of Life revealed by their representation of the seven musical scales is shown in Figure 11.
Including the tonic and octave creates 64 pairs of intervals and their complements. This suggests a connection with the 64 hexagrams, each a pair of trigrams, of the I Ching table, which we will now explore. The pair of Heaven trigrams in the top left-hand corner of the table symbolise the tonic and the octave. Their six lines correspond to the six Sephiroth on either side of the central Pillar of Equilibrium that coincide with corners of the first (6+6) polygons outside their root edge. These points are interfaces between the outer and inner Trees of Life and can be regarded as the source of the latter. The 63 other hexagrams have 378 Yang/Yin lines. They correspond to the 378 yods in these polygons other than the six yods that coincide with these Sephiroth. They symbolize the 378 rising/falling intervals between the notes of the seven scales. These are grouped into 63 rising intervals, their 63 complements and 63 unpaired intervals, that is, as 63
8
9
groups of three rising intervals. There are 63 groups of three falling intervals. Therefore, the 378 intervals naturally group into 63 pairs of triplets of intervals, one pair denoting rising intervals and the other denoting falling intervals. One trigram in a hexagram symbolizes three rising intervals and the other trigram symbolizes a triplet of falling intervals. The 42 Yang/Yin lines in the seven other diagonal hexagrams denote the 42 rising/falling intervals between the tonic and the notes with tone ratios up to 1024/729. They correspond to the 42 yods at the centres of the 42 triangles of the Sri Yantra and to the 42 corners of the (6+6) polygons outside their shared edge. The 42 remaining intervals (not notes) and their 42 complements correspond to the 42 Yang lines and the 42 Yin lines in the upper trigrams of the 28 hexagrams on one side of the diagonal of the I Ching. The 21 complements of the notes and the 63 unpaired intervals correspond to the 84 lines in the lower trigrams of these hexagrams. The 168 lines and broken lines in the 28 hexagrams denote the 168 rising intervals other than the 21 notes in the seven scales up to the one with the largest tone ratio 1024/729. Their 168 mirror image counterparts below the diagonal denote the 168 corresponding falling intervals. The I Ching
table is a symbolic representation of the composition of intervals between the notes of the seven scales. Figure 12 shows the correspondence between the table and the Sri Yantra.
There are no more than 24 perfect fourths in the 189 intervals that are matched by perfect fifths. This is remarkable in view of the fact7 established in Article 38 that the intervals between the 14 types of notes of the seven scales can group into no more than 24 pairs of intervals and their complements. The numbers 24 and 48 play a pivotal role both for the 14 basic notes and for the seven scales that they form. It is further evidence that possessing the feature of 24 pairs of objects is fundamental to any holistic system. For example, in the I Ching table, it is the 24 Yang lines and 24 Yin lines of the eight diagonal hexagrams. In the inner Tree of Life, it is the 24 pairs of corners outside the root edges of the first (6+6) polygons. In the Klein Configuration, it is the 24 heptagons representing the 168 automorphisms of the Klein Quartic and the 24 heptagons representing its 168 anti-automorphisms. In the Sri Yantra, it is the 24
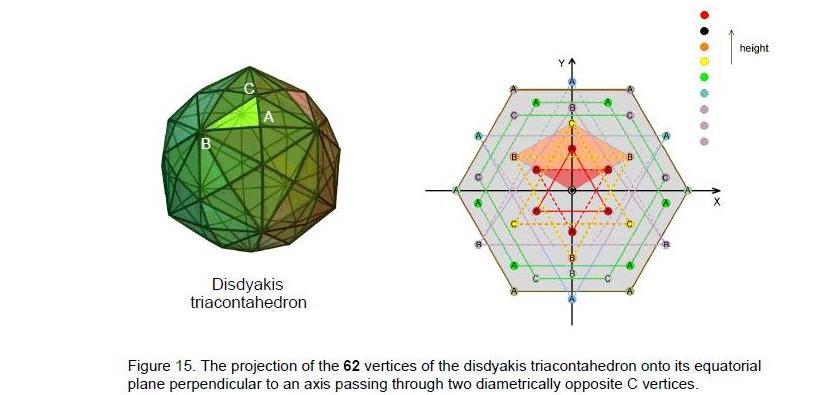
10
pairs of hexagonal yods on the 24 edges of the eight triangles in its lowest layer. In the disdyakis triacontahedron, it is the 24 pairs of vertices on either side of its equator that surround an axis passing through two diametrically opposite A vertices.
The octave is common to the seven scales. Including the latter as a single interval, they have 190 intervals. 190 is the sum of the first 19 integers, where 19 is the tenth odd integer. This demonstrates how the Decad (10), called “All Perfect” and “Key-holding” by the ancient Pythagoreans, determines how many intervals exist between the notes of the seven musical scales. It also determines the 12 types of note intervals in the seven scales below the octave with tone ratio 2 because 12 is the tenth integer after 2.
Earlier, we found that there are 137 Pythagorean intervals in the seven scales if their tonics 1 are included. The 189 intervals contain 54 perfect fourths and fifths. There are 135 intervals other than these between the tonic and octave. Including the latter as single notes, there are 137 intervals other than perfect fourths and fifths between the 44 notes of the seven scales. 137 is the 33rd prime number, where 33 = 1! + 2! + 3! + 4!. This shows how this number is defined by the Pythagorean integers 1, 2, 3 & 4 symbolized by the tetractys. The Godname ADONAI with number value 65 prescribes the 66 non-Pythagorean intervals among the 189 intervals because 66 is the 65th integer after 1.
There are 123 Pythagorean intervals among the 189 intervals. The 378 rising and falling intervals contain 246 rising and falling Pythagorean intervals. 246 is the number value of Gabriel, Archangel of Yesod. Including the octave, there are 248 rising and falling Pythagorean intervals. 248 is the number of gauge bosons of the superstring gauge symmetry group E8 that transmit its unified interaction. This proves the parallel between superstring physics and properties of the seven musical scales.
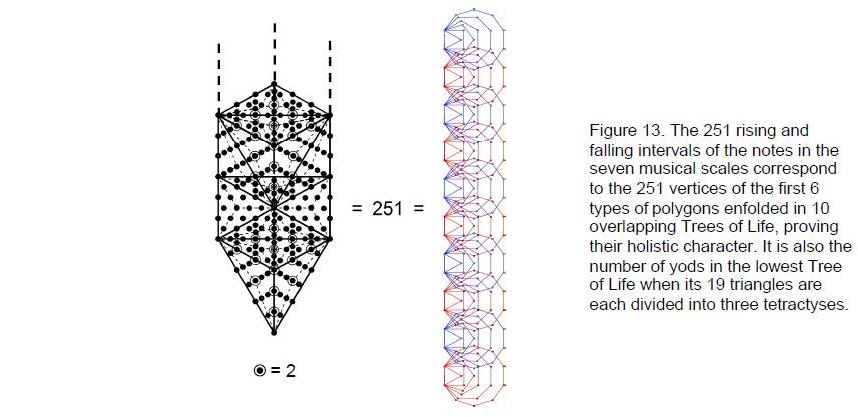
There are 125 intervals with tone ratios up to 1024/729. Including the tonic, there are 251 rising and falling intervals up to this largest note before the complements. This number is the number of vertices of the 60 polygons of the first six types enfolded in 10 overlapping Trees of Life (Fig. 13). The 30 polygons enfolded in five Trees of Life have 126 corners — the number of rising intervals up to 1024/729 in the seven scales if the tonic is included. Therefore, the 251 vertices are made up of 125 vertices intrinsic to the 30 polygons enfolded in the lowest five trees, one vertex shared with the polygons enfolded in the sixth tree and 250 vertices intrinsic to the five highest trees. This is the Tree of Life representation of the 125 falling intervals less than 1, the interval 1 and the 125 rising intervals up to 1024/729. As the 10 overlapping Trees of Life are the Tree of Life representation of the 10 Sephiroth, this proves the holistic nature of the seven musical scales.
Every single rising and falling interval between its notes can be assigned to the 251 vertices of its inner form. They can also be assigned to the 251 yods that make up the 19 triangles of the lowest of any set of Trees of Life when they are each divided into three tetractyses. This is further remarkable confirmation of the
11
holistic nature of the seven scales. The significance of the number 251 for the 10-fold heterotic superstring and, more generally, for the mathematical map of the seven planes of consciousness, was discussed in Article 5.8
The 14 outermost points of the triangles in the fourth layer of triangles were interpreted in Article 36 in terms of the 14 different notes of the seven scales, with the six points that touch the circumscribing circle symbolizing the six non-Pythagorean notes and the eight points that do not touch it denoting the eight Pythagorean notes. The analysis of this article offers another level of meaning. According to the table on page 6 listing the numbers of paired intervals other than notes, the 42 pairs of intervals other than notes contain two leimmas and five tone intervals. These are the fundamental intervals generating the seven scales and so it is fitting that they should be symbolized by the seven tips of the triangles in the last layer, their falling intervals L–1 and T–1 being denoted by the seven tips diametrically opposite them (Fig. 14). This means that the seven tips represent the rising interval of an octave T5L2 = 2 and their mirror images represent the falling interval of an octave T–5L–2 = ½. What this feature of the Sri Yantra is telling us is that not only are there seven intervals and their falling counterparts to a musical scale but also seven types of tone intervals and their falling counterparts that exist in the seven kinds of musical scales.
2. The disdyakis triacontahedron encodes the 378 musical Intervals.
The 60 vertices of the disdyakis triacontahedron that surround an axis passing through two diametrically opposite C vertices are arranged in 15 layers.9 Starting from the top, there is an equilateral triangle with three A vertices, then a C vertex, an inverted triangle with three B vertices, a triangle with three C vertices, a six-sided polygon with six A vertices, an inverted triangle with three A vertices, a six-sided polygon with six C vertices, a triangle with three B vertices and a hexagon with six A vertices. The seven
other polygons are mirror images of the first seven, so there are eight distinct polygons.
Constructed from triangles, the 15 polygons were shown in Article 3610 to possess 240 vertices, edges and triangles surrounding their centres. This number is a basic structural parameter of the Tree of Life, and so it should not be surprising that it
12
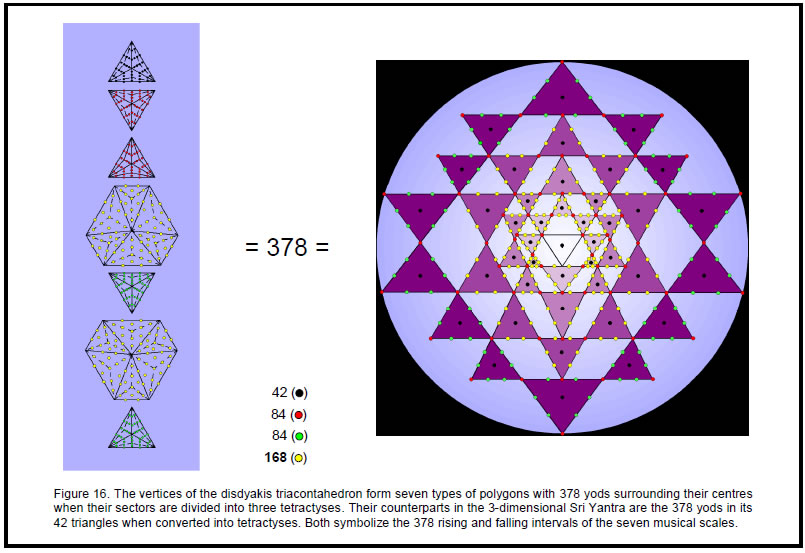
reappears in its polyhedral version — the disdyakis triacontahedron. It was also shown11 in the same article that, together with the two C vertices forming the axis, the 15 polygons have 137 vertices when their sectors are divided into three triangles. Compare this with the fact that the seven scales have 137 Pythagorean intervals if their tonics are included. It raises the question whether the 15 polygons, or some subset of them, embody the fact that the seven scales have 378 rising and falling intervals. As we shall now prove, they, indeed, do have this remarkable property.
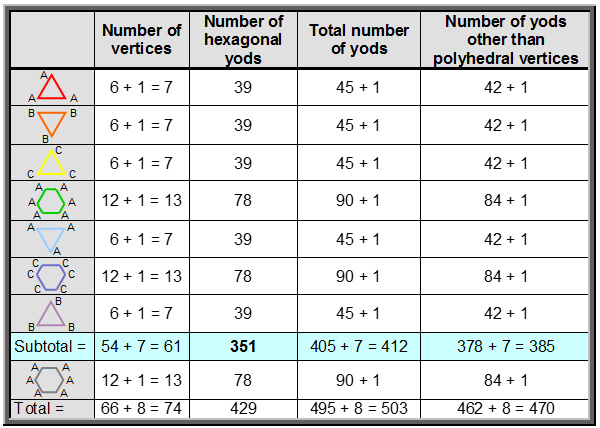
Table 12 shows the number of yods in the eight types of polygons when their sectors are divided into three triangles and each triangle turned into a tetractys.
Table 12. Number of yods in the eight types of polygons (sectors as three tetractyses).
Surrounding the centre of each triangle are 42 yods other than their polyhedral vertices. Surrounding the centres of the 6-sided polygons are 84 yods other than their polyhedral vertices. Surrounding the centres of the six polygons above the hexagon in the middle are 378 yods other than their 27 polyhedral vertices (see highlighted row in Table 12). This is the number of rising and falling intervals in the seven scales! Moreover, this cannot be a coincidence because the yod populations of each polygon are the number of the different groups of intervals. Compare the numbers in the right-hand column of Table 12 with the numbers of various groups of intervals calculated earlier:
378 rising/falling intervals = 21 pairs of notes & complements + 42 pairs of intervals other than notes + 63 unpaired intervals
= 21 rising note intervals +
21 falling note intervals + 21 rising complements +
21 falling complements + 42 rising intervals other than notes + 42 falling
intervals other than notes + 42 rising complements other than notes + 42 falling
complements other than notes + 63 rising, unpaired
intervals + 63 falling, unpaired intervals
13
14
= 42 rising/falling notes + 42 falling intervals other than notes + 42 rising intervals other than notes + 42 rising complements + 42 falling complements other than notes + (21 rising complements + 63 rising, unpaired intervals)
= 84 rising intervals) + (21 falling complements + 63 falling, unpaired intervals) (= 84 falling intervals).The numbers of yods in the seven polygons formed by the vertices of the disdyakis triacontahedron are precisely the numbers of different groups of intervals. The number 42 has the factorisation 7×3×2, where ‘7’ is the number of scales, ‘3’ is the number of notes or the number of complements and ‘2’ refers to the rising or falling nature of the interval. A possible correlation between the polygons and the intervals that they encode is shown below:
Other assignments are possible. Whatever is the correct one, the crucial fact is that the seven types of polygons have as many yods surrounding their centres as there are both musical intervals and yods making up the Sri Yantra. This is because all three are different forms of the same universal, mathematical paradigm. Other than the first three rising and falling intervals in each scale, there are 168 rising intervals and 168 falling intervals, i.e., 336 intervals other than these independent intervals. This shows how the
superstring structural parameters 168 and 336 are related to the musical scales and therefore have an analogous, mathematical basis.
15
Figure 16 shows the correspondence between the seven types of polygons formed by the vertices of the disdyakis triacontahedron and the 3-dimensional Sri Yantra. The 84 vertices of the 42 triangles in the latter correspond to the second and third triangles, which encode the 84 rising and falling intervals other than notes. The 42 black yods at the centres of these triangles correspond to the first triangle, which encodes the 42 rising and falling notes. The 84 green hexagonal yods lying on the edges of the 14 triangles in the fourth layer of the Sri Yantra correspond to the fourth and fifth triangles, which encode the 84 rising and falling complements other than notes. The 168 yellow hexagonal yods in the first three layers correspond to the two 6-sided polygons, which
Table 13. The gematria number values of the 10 Sephiroth in the four Worlds.
Sephirah
Angels
ChakraKether Chokmah Binah Chesed Geburah Tiphareth Netzach Hod Yesod Malkuth encode the 168 rising and falling intervals that are either complements or unpaired intervals.
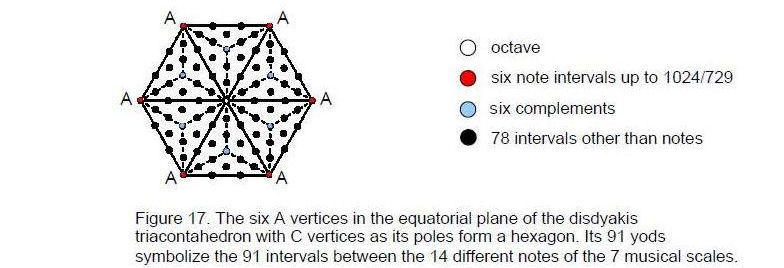
The hexagon with six A vertices in the equatorial plane of the disdyakis triacontahedron has 91 yods when its sectors are each constructed from three tetractyses (Fig. 17). They symbolize the 91 intervals between the 14 different types of notes found in the seven musical scales. The six A vertices and the six internal vertices symbolize, respectively, the six notes and their complements between the tonic and the octave, which is denoted by the yod at the centre of the hexagon. The 78 hexagonal yods denote the intervals between them. The first seven polygons embody the patterns of intervals of the seven scales taken separately and the eighth polygon embodies information about their different notes and their intervals now regarded as a whole. This collective information encoded in the yod population of the hexagon manifests in the shape of the disdyakis triacontahedron. The 90 ascending intervals and the 90 descending intervals other than the octave are geometrically represented by, respectively, the 90 edges of the polyhedron and their mirror images. Truly, the inner Tree of Life, the I Ching table, the Sri Yantra and the disdyakis triacontahedron are isomorphic representations of the seven musical scales.
_______________________
References
1 Numbers highlighted in boldface are the number values of the Hebrew names of the Sephiroth, their Godnames, Archangels, Orders of Angels & Mundane Chakras. They are listed above in Table 13.2 Phillips, Stephen M. Article 17: “The Logarithmic Spiral Basis of the Titius-Bode Law,” (WEB, PDF), p. 3.
16
3 Phillips, Stephen M. Article 32: “Derivation of the Bones & Classical Acupoint Compositions of the Human Body and Their Relationship to the Seven Musical Scales,” (WEB, PDF), pp. 7–8.
4 Phillips, Stephen M. Article 35: “The Tree of Life Nature of the Sri Yantra and Some of its Scientific Meanings,” (WEB, PDF), p. 11, Table 5.
7 Phillips, Stephen M. Article 38: “The Geometrization of the Seven Musical Scales and its Mathematical Implications,” (WEB, PDF), p. 7.
8 Phillips, Stephen M. Article 5: “The Superstring as Microcosm of the Spiritual Macrocosm,” (WEB, PDF), pp. 9, 17–22.
9 Phillips, Stephen M. Article 36: “The Sri Yantra-like Pattern of the 15 Layers of Vertices in the Disdyakis Triacontahedron and its Scientific Meaning,” (WEB, PDF).
17