| << Previous 1... 37 38 [39] 40 41 ...50 Next >> |
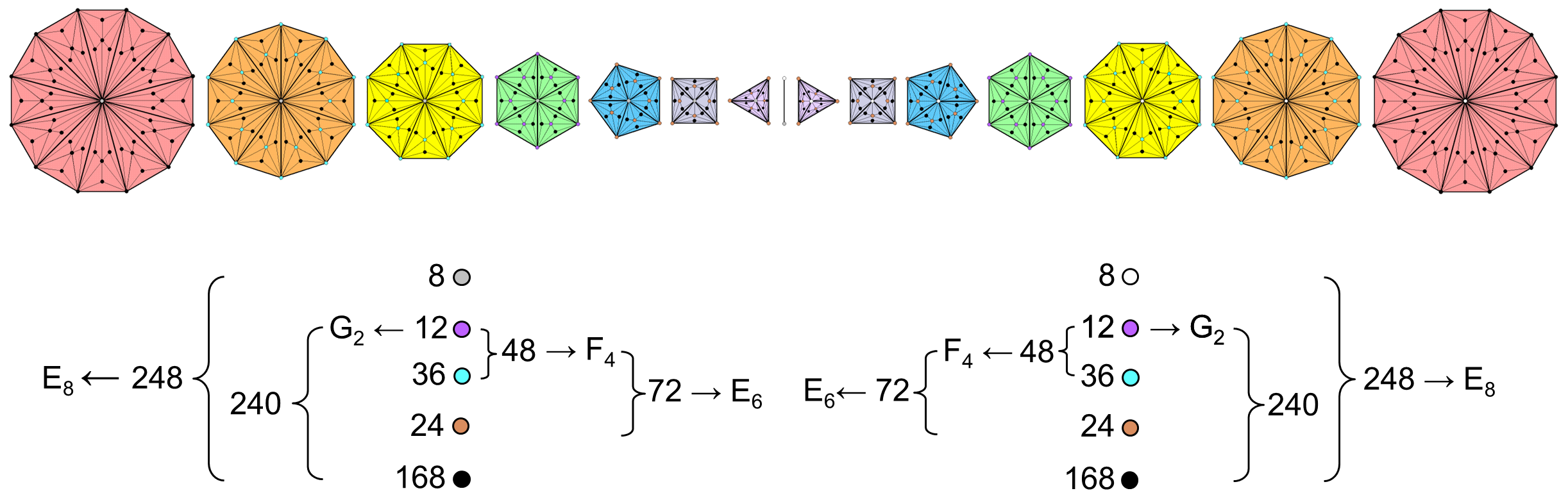
The inner Tree of Life representation with Type C polygons of the heterotic superstring symmetry group E8×E8′

A Type C polygon is a polygon whose sectors are Type B triangles with seven corners and 15 sides of nine basic triangles, i.e., 31 geometrical elements, where 15 is the number value of YAH, the Godname of Chokmah, and 31 is the number value of EL, the Godname of Chesed. This means that each sector contributes 28 geometrical elements (5 corners, 14 sides & 9 triangles). The 9n triangles in a Type C n-gon have (5n+1) corners (see also here), where "1" denotes its centre. The seven separate Type A polygons in each half of the inner Tree of Life have 48 sectors with 55 corners. The 48 sectors in the seven Type C polygons are composed of (∑9n = 9×48 = 432) triangles. The number of their corners = ∑(5n+1) = 5×48 + 7 = 247. Surrounding the centres of the seven polygons are 240 corners. This compares with the 240 hexagonal yods that surround the centres of the seven polygons when they are Type A (see here). As a defining parameter of holistic systems, the number 240 reappears in different levels of differentiation of their sacred geometries. In the case of the seven separate Type B polygons, it appears as the 240 sides of the 144 triangles making up their 48 sectors. If we consider a straight line representing the root edge separating each set of seven separate Type C polygons, its two endpoints can be formally regarded as corners. One endpoint is associated with one set of polygons and the other endpoint is associated with its mirror image set. Hence, 248 corners are associated with each set of polygons separated by a line representing their root edge. The diagram above indicates that the white centres of the seven polygons and one endpoint of the root edge denote the eight simple roots of E8, the eight grey centres of the other set of seven polygons denote the eight simple roots of E8′ and the 240 corners of the 432 triangles in each set of polygons denote the 240 roots of E8 or E8′. 248 is the number value of Raziel, the Archangel of Chokmah. It is also the dimension of E8, the rank-8, exceptional Lie group. We saw on page 29 of this section that the pair of joined Type C triangles have 248 intrinsic yods unshared with the outer Tree of Life. This embodiment of E8 in the simplest polygon and the first member of the set of seven regular polygons making up the inner Tree of Life manifests again in the skeletal pattern of 248 corners associated with all seven members of each set. The 14 Type C polygons separated by their root edge have 496 corners, where 496 is the number of Malkuth and the dimension of E8×E8′ and SO(32), the two symmetry groups that describe superstring forces that are free of quantum anomalies. The mirror symmetry of the two halves of the inner form of the Tree of Life favours E8×E8′, for it is the geometrical reason for the superstring gauge symmetry group being the direct product of two identical groups.
Evidence that this correspondence between sacred geometry and the group symmetry of heterotic superstring forces is not coincidental is provided by the following analysis of how subsets of corners correspond to the four exceptional Lie groups G2, F4, E6 & E7 that are subgroups of E8.
If the group A with m roots is a subgroup of a group B with n roots, the set of m corners that correspond to the former must be a subset of the set of n corners that correspond to the latter. A number N that is the numbers of roots in an exceptional group will be underlined (i.e., N). The number (n) of corners in a single polygon will be written in bold-face (i.e., n). To avoid possible confusion, the numbers of the ten Sephiroth, their Godnames etc, which have been written in bold throughout this website, will be left unformatted. As E8⊃E7⊃E6⊃F4⊃G2, where E8 has 240 roots, E7 has 126 roots, E6 has 72 roots, F4 has 48 roots & G2 has 12 roots, the 240 corners of the 432 triangles in the 48 sectors of the seven separate polygons that symbolise the lattermost must be split up into sets (n) of n corners that display the divisions:
240 = 126 + 114 = 72 + 168,
where
126 = 72 + 54,
72 = 48 + 24,
and
48 = 12 + 36.
Therefore,
168 = 54 + 114.
The five corners per sector of a Type C polygon consist of the two corners per sector of a Type B polygon and three corners added by converting the polygon from Type B to Type C. “2*” will denote the former and “3*” will denote the latter (“N×M” will mean N multiplied by M). Therefore,
240 = 48×2* + 48×3*.
Let
72 = m×2* + n×3* (3≤m; n≤48)
i.e.,
72 = 2m + 3n.
As 72 & 2m are even numbers, 3n is also even, which means that, as 3 is an odd integer, n is an even integer, i.e., n = 2q (q an integer). Therefore,
72 = 2m + 6q,
that is,
m/3 = 12 – q.
As 12 and q are integers, m/3 is an integer, so that m = 3p (p an integer) and p + q = 12. The table below lists the 13 possible combinations of the values of p & q:
|
p |
q |
72 = 6p + 6q = 48 + 24 = 12 + 36 + 24 |
Comment |
|
|
1. |
0 |
12 |
24×3* |
Preferred |
|
2. |
1 |
11 |
3×2* + 22×3* |
Disallowed |
|
3. |
2 |
10 |
6×2* + 20×3* |
|
|
4. |
3 |
9 |
9×2* + 18×3* |
|
|
5. |
4 |
8 |
12×2* + 16×3* |
|
|
6. |
5 |
7 |
15×2* + 14×3* |
|
|
7. |
6 |
6 |
18×2* + 12×3* |
|
|
8. |
7 |
5 |
21×2* + 10×3* |
|
|
9. |
8 |
4 |
24×2* + 8×3* |
|
|
10. |
9 |
3 |
27×2* + 6×3* |
|
|
11. |
10 |
2 |
30×2* + 4×3* |
|
|
12. |
11 |
1 |
33×2* + 2×3* |
Disallowed |
|
13. |
12 |
0 |
36×2* |
Preferred |
Possibility 2 is disallowed because it requires 12 = 3×2* + 2×3*, but there is no polygon with just two sectors. Possibility 12 is disallowed for the same reason because it requires 12 = 3×2* + 2×3*.
72 = 12 + 36 + 24.
Let
12 = a×2* + b×3* (0≤a≤6; 0≤b≤4)
i.e.,
12 = 2a + 3b.
As 12 & 2a are even numbers, so is 3b, which means that b = 2c (c an integer). Therefore,
6 = a + 3c,
that is,
a/3 = 2 – c.
Therefore, a = 3d (d an integer) and c + d = 2. The table below lists the three possible cases:
|
c |
d |
12 |
|
| Case A |
0 |
2 |
6×2* |
| Case B |
1 |
1 |
3×2* + 2×3* |
| Case C |
2 |
0 |
4×3* |
Case
A
This applies to possibilities 3-13. We shall consider only
possibility 13. This is because it seems, intuitively, to be the correct one in that it identifies the
72 roots of E6 purely with 36 pairs of corners of triangles in polygons considered as Type B,
i.e., it does not mix corners from Type A and Type B polygons. As 12 sectors of complete polygons may
be chosen from either the dodecagon, the square & the octagon or the triangle, the square & the
pentagon, there are three possible ways the 36 sectors may be selected so as to leave 12 sectors:
1. The first six polygons have 36 sectors with 72 corners when they are Type B. As this subset of the seven polygons has been shown elsewhere in this website to constitute another holistic system, it seems a natural candidate for the correct choice of the corners that represent the 72 roots of E6, one of the exceptional subgroups of E8.
72 = (3+4+5+6+8+10)×2* = (6+8+10)×2* + (3+4+5)×2* = 48 + 24,
where 48 = (6+8+10)×2 = 6×2* + (8+10)×2* = 12 + 36,
where 12 = 6×2*. Therefore,
72 = (3+4+5)×2* + (6+8+10)×2* = 24 + 2×24 → 3×24,
and
168 = 240 − 72 = (3+4+5+6+8+10)×3* + 12×(2*+3*) = (3+4+5+12)×3* + (6+8+10)×3* + 12×2* = 3×24 + 3×24 + 24 → 7×24.
Notice that:
168 = [(3+4+5)×3* + 8×3* + 12×2*] + [12×3* + (6+10)×3*] = 84 + 84.
This is a required property of any inner Tree of Life representation of the superstring structural parameter 168 because it is found in many other sacred geometries and is characteristic of holistic systems in general (see The Holistic pattern).
2. 72 = (3+5+6+10+12)×2* = (3+5+6+10)×2* + 12×2* = 48 + 24,
where 48 = (3+5+6+10)×2* = 12 + 36,
where 12 = 6×2*. Therefore,
72 = 2×24 + 24 → 3×24,
and
168 = 240 − 72 = (4+8)×2* + (3+4+5+6+8+10+12)×3* = (4+8)×2* + (3+4+5+12)×3* + (6+8+10)×3* = 24 + 3×24 + 3×24 → 7×24.
Notice that:
168 = [(6+10+12)×3*] + [(4+8)×2* + (3+4+5+8)×3*] = 84 + 84.
3. 72 = (6+8+10+12)×2* = (6+8+10)×2* + 12×2* = 48 + 24,
where 48 = (6+8+10)×2* = 6×2* + (8+10)×2*,
where 12 = 6×2*. Therefore,
72 = 2×24 + 24 → 3×24,
and
168 = 240 − 72 = (3+4+5)×2* + (3+4+5+6+8+10+12)×3* = (3+4+5)×2* + (3+4+5+12)×3* + (6+8+10)×3* = 24 + 3×24 + 3×24 → 7×24.
Notice that:
168 = [(6+10+12)×3*] + [(3+4+5)×2* + (3+4+5+8)×3*] = 84 + 84.
Case B
This is disallowed as it has two sectors, each with three corners, and there is no polygon with two sectors.
Case C
This applies to possibility 1 and possibilities 3-11. We shall consider only possibility 1. This is because all the 72 corners here are of the same type, i.e., the extra three corners per sector introduced by turning Type B polygons into Type C polygons. The 24 sectors may be chosen from three possible sets of polygons:
1. Triangle, square, pentagon & dodecagon.
72 = (3+4+5+12)×3* = [4×3* +12×3*] + (3+5)×3* = 48 + 24 → 3×24.
48 = 4×3* + 12×3* = 12 + 36,
where 12 = 4×3*. Therefore,
168 = 240 − 72 = (3+4+5+12)×2* + (6+8+10)×(2*+3*) = 2×24 + 2×24 + 3×24 → 7×24.
Notice that:
168 = [(3+4+5+12)×2* + 6×2* + 8×3*] + [(8+10)×2* +(6+10)×3*] = 84 + 84.
2. Hexagon, octagon & decagon.
72 = (6+8+10)×3* = 48 + 24,
where 48 = 6×3* + 10×3*. As F4⊃G2, 48 = 12 + 36. As the derived composition of 48 into a set of 18 corners and a set of 30 corners is incompatible with the 48 roots of F4 including a set of 12 represented by one polygon, this possibility is disallowed.
3. Square, octagon & dodecagon.
72 = (4+8+12)×3* = 4×3* + 12×3* + 8×3* = 48 + 24 → 3×24.
48 = 4×3* + 12×3* = 12 + 36,
where 12 = 4×3*. Therefore,
168 = 240 − 72 = (3+4+5+6+8+10+ 12)×2* + (3+5+6+10)×3* = (3+4+5)×2* + (6+8+10)×2* + 12×2* + (3+5)×3* + (6+10)×3* = 24 + 2×24 + 24 + 24 + 2×24 → 7×24.
Notice that
168 = [(3+4+5+6)×2* + (6+10)×3*] + [(8+10+12)×2* + (3+5)×3*] = 84 + 84.
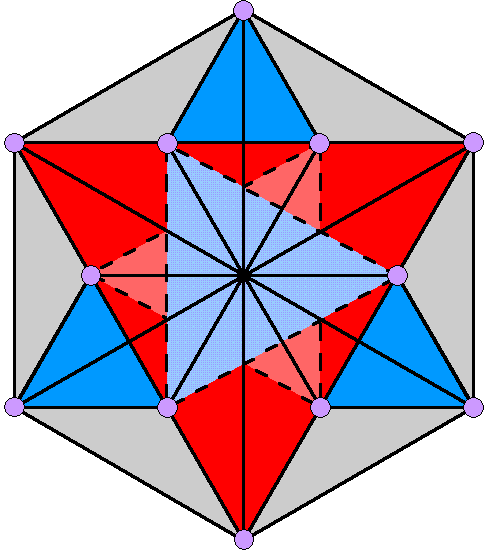
Both case A and case C are consistent with the root composition of the exceptional subgroups of E8. They also respect the factorizations: 72 = 3×24 and 168 = 7×24 (and, therefore, the factorisation 240 = 10×24) found in sacred geometries embodying these superstring parameters (e.g., see Article 53, here & here), as well as the split: 168 = 84 + 84, which, too, manifests in these geometries (see The holistic pattern). Which of the five deduced possibilities is the correct one? In case A, the 12 roots of G2 correspond to the six pairs of corners in the hexagon when it is Type B. In case C, they correspond to the four sets of three corners in the Type C square added by conversion from its Type B version. The plot of these 12 roots αi & αi' (i=1-6) in 3-dimensional space generates two Stars of David, one nesting inside the other, i.e., four triplets of points that group into six pairs (αi, αi') (see p. 26 in Article 32). This property is more consistent with the geometry of case A, which consists of a larger Star of David formed by the corners of the hexagon and a smaller one formed by the centres of its Type A triangular sectors:
 |
|
|
|||||||||||||
|
The 12 corners of the 18 triangles in a Type B hexagon surrounding its centre form two nested Stars of David. |
The 12 roots of G2 (shown as coloured dots) form two
nested Stars of David with its two simple roots at vertices of each star (shown as black circles). Dots of the same colour denote a root and its inverted counterpart. |
||||||||||||||
However, qualitative similarity with a group-theoretical property of G2 is insufficient in order to choose with mathematical certainty between the Type C square and hexagon as the representation of this group. The diagram displaying the correspondence between corners and roots is based upon possibility 1 in case A. This possibility is the most appealing one, intuitively speaking, because it makes E6 correspond to the first six polygons, which, as considerable evidence amassed though out this website has shown, constitutes a holistic system in itself. It is well-known that E6 can accommodate the Standard Model of particle physics, so it is highly plausible that the (almost) complete physics that it represents should be contained in the first six polygons. Amazingly, in the case of the two joined Type C hexagons, 248 yods outside their shared root edge surround the centre of each hexagon (see discussion on page 16 in Wonders of Superstrings). This is an example of the Tetrad Principle in action (see Article 1), for the hexagon is the fourth regular polygon and the Type C hexagon is the fourth of this type of polygon:
hexagon → Type A hexagon → Type B hexagon → Type C hexagon → ....
We discover that this pivotal polygon embodies not only the root pattern of the smallest exceptional group G2, when it is Type B, but also the roots of the largest exceptional group E8, when the hexagon is Type C. Article 60 also discusses how the Type C hexagon embodies both the superstring structural parameter 168 and the superstring dynamical parameter 496. The latter is discussed under the heading "Hexagon" on page 29 at Miscellaneous Wonders. It is known that G2 is the group of automorphisms of the octonions, whose algebra is represented by the Fano plane. Its group of 168 isomorphisms is SL(2,3), which is isomorphic to PSL(2,7), the group of 168 automorphisms of the Klein quartic equation discussed in Article 15. Some physicists believe that the 8-dimensional octonions provide a natural basis for the rank-8, exceptional group E8. In view of this, it should come as no surprise that the Type C hexagon "contains" not only G2 but E8. In other words, the simplest and the most complex of the five exceptional groups have the same polygon as their source!
| << Previous 1... 37 38 [39] 40 41 ...50 Next >> |