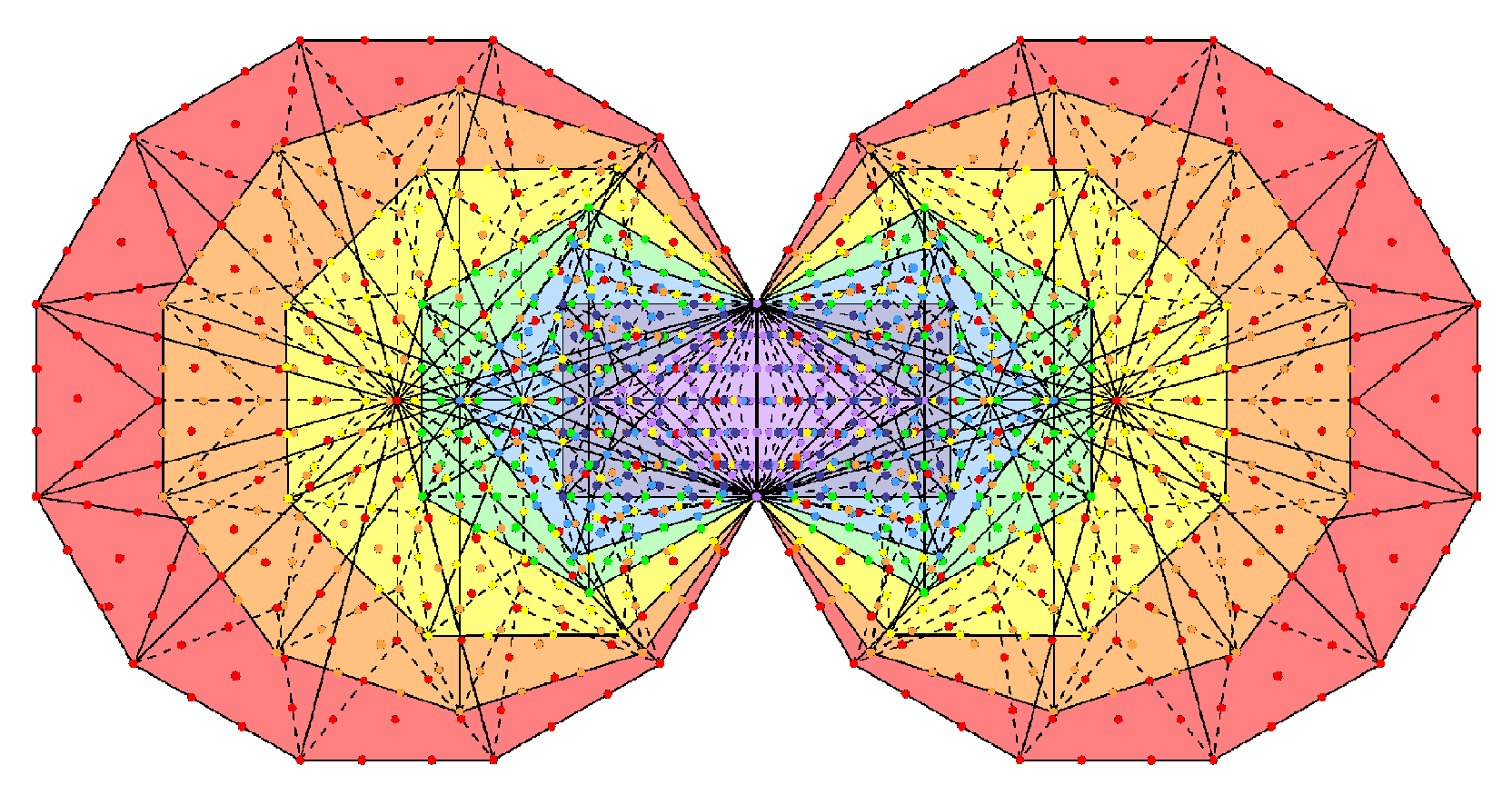
The (7+7) enfolded Type B polygons contain 1370 yods (for proof, see Table 3 here). This parameter has a representation in terms of powers of 2. To derive it, start with the arithmetic identity:

84 = 2² + 4² + 8² = 2² + 2⁴ + 2⁶.

∴ 168 = 2×84 = 2³ + 2⁵ + 2⁷,

336 = 2×168 = 2⁴ + 2⁶ + 2⁸,

and

672 = 2×336 = 2⁵ + 2⁷ + 2⁹.

 ∴1370 = 26 + 1344 = 26 + 672×2,

where

26 = 2 + 8 + 16 = 2¹ + 2³ + 2⁴.

∴ 1370 = 2¹ + 2³ + 2⁴ + 2⁶ + 2⁸ + 2¹⁰.

Geometrical interpretation

• The first term "2¹" (=2) denotes the topmost corners of the pair of hexagons, which coincide with the bottom corners of the pair of hexagons enfolded in the inner form of the next higher Tree of Life. There remain 1368 yods that are intrinsic to (that is, unshared with) the inner forms of successive, overlapping Trees of Life, where

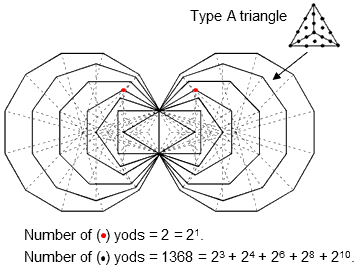
1368 = 2³ + 2⁴ + 2⁶ + 2⁸ + 2¹⁰.

• The second term "2³" (=8) denotes the 8 hexagonal yods on the side pillars of the outer Tree of Life that are shared with the two hexagons. 1360 yods intrinsic to each set of (7+7) enfolded Type B polygons are left, where

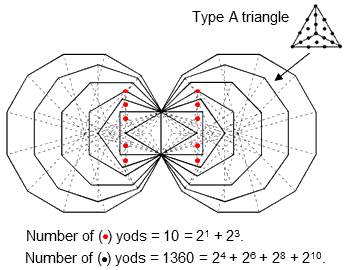
1360 = 2⁴ + 2⁶ + 2⁸ + 2¹⁰

        = 4² + 4³ + 4⁴ + 4⁵.

This demonstrates the remarkable power of the Tetrad (4) to express various population parameters of holistic systems like the inner Tree of Life. This is further illustrated by the fact that 1360 = 10×136 = (1+2+3+4)×136, where

	1	2	3	4
136 =	5	6	7	8
	9	10	11	12
	13	14	15	16

 is the sum of the first (16=4²) integers. The yod population 1360 is that of 136 tetractyses.

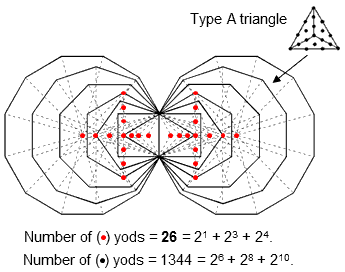
• The third term "2⁴" (=16) denotes the 8 yods in each set of 7 enfolded polygons that are either the lowest corners of the two hexagons shared with the outer Tree of Life or centres of the (7+7) polygons. This leaves 1344 yods that are intrinsic to the (7+7) enfolded polygons and surround their centres, where

1344 = 2⁶ + 2⁸ + 2¹⁰ = 4³ + 4⁴ + 4⁵.

Each set of 7 enfolded Type B polygons contains 672 such yods, where

672 = 2⁵ + 2⁷ + 2⁹.

There are 13 other yods in each set of 7 enfolded polygons (12 intrinsic) that are either shared with the outer Tree of Life (6) or centres of polygons (7), where

13 = 1 + 4 + 8 = 2⁰ + 2² + 2³.

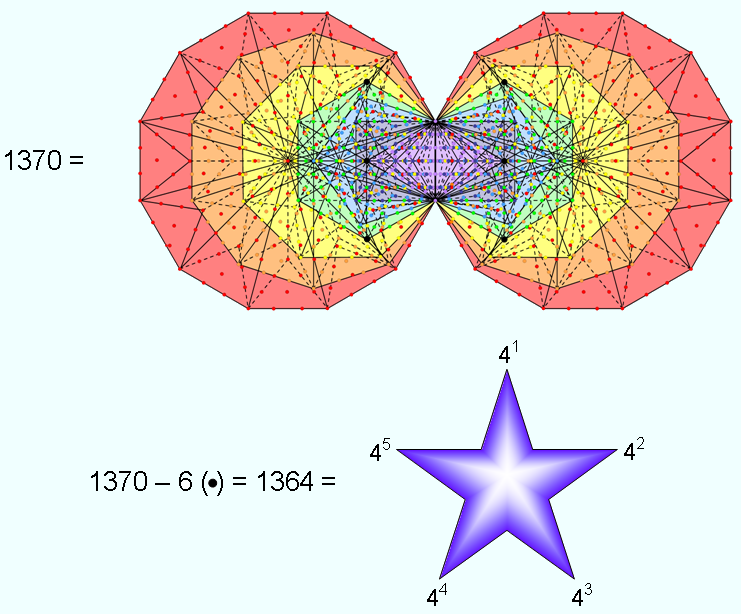
Six of the 1370 yods in the (7+7) enfolded Type B polygons are located at the positions of the 6 Sephiroth on the side pillars of the outer Tree of Life. They are shown above as black dots. There are (1370−6=1364) other yods, i.e., (1364−4=1360) yods outside the root edge, where

1360 = 4² + 4³ + 4⁴ + 4⁵ = 2⁴ + 2⁶ + 2⁸ + 2¹⁰.

∴ 1364 = 4¹ + 4² + 4³ + 4⁴ + 4⁵ = 2² + 2⁴ + 2⁶ + 2⁸ + 2¹⁰.

This demonstrates in a beautiful way the power of the Tetrad to express parameters of the inner Tree of Life.

As

1370 = 2¹ + 2³ + 2⁴ + 2⁶ + 2⁸ + 2¹⁰,

the number of yods associated with each set of 7 enfolded polygons = 685 = 2⁰ + 2² + 2³ + 2⁵ + 2⁷ + 2⁹,

the number of yods in each set = 685 + 2 = 687 = 2⁰ + 2¹ + 2² + 2³ + 2⁵ + 2⁷ + 2⁹,

and the number of intrinsic yods outside the root edge in each set = 687 − 4 − 1 = 682 = 2¹ + 2³ + 2⁵ + 2⁷ + 2⁹.

This provides an alternative interpretation of the number 1364 (=2×682): it is the number of yods outside the root edge in the inner form of successive Trees of Life. The latter is designed in such a way that 1364 = 4¹ + 4² + 4³ + 4⁴ + 4⁵. Very beautiful, don't you think? And not a coincidence ......

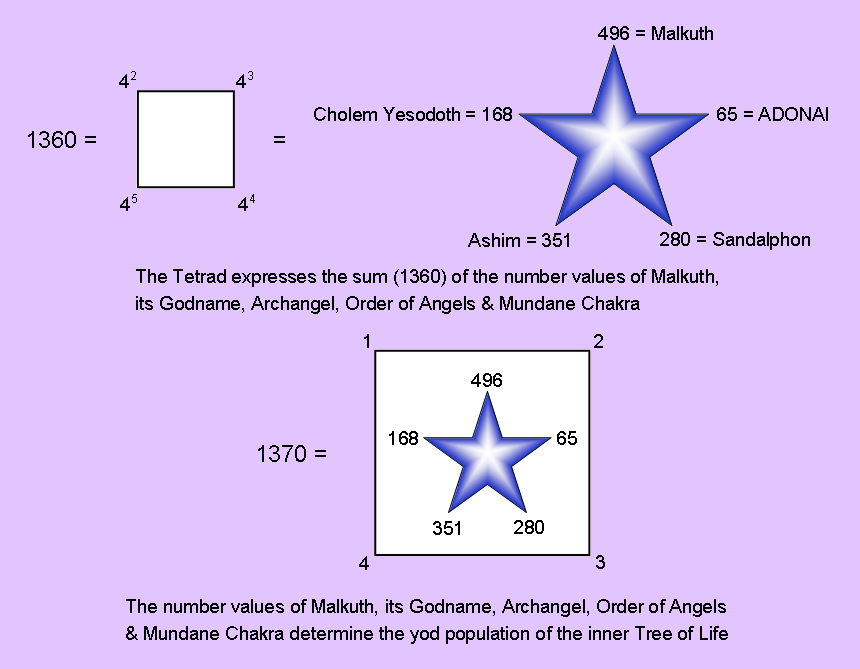
There are 1360 yods outside the root edge not coinciding with the positions of the 6 Sephiroth on the two side pillars of the outer Tree of Life. It is remarkable that this number is the sum of the gematria numbers of Malkuth (496), its Godname ADONAI (65), its Archangel Sandalphon (280), its Angelic Order Ashim (351) and its Mundane Chakra Cholem Yesodoth (168):

1360 = 496 + 65 + 280 + 351 + 168.

The total yod population of the (7+7) enfolded Type B polygons (1370) can be represented as a pentagonal array of these numbers enclosed in a square with the Pythagorean integers 1, 2, 3 & 4 assigned to its corners. The number 4 denotes the 4 yods in the root edge and the sum (6) of the integers 1, 2 & 3 denotes the 6 yods at the positions of the 6 Sephiroth on the two side pillars.

Interpretation in terms of the 4₂₁ polytope

The inner form of the n-tree consists of n sets of (7+7) enfolded polygons, the topmost corners of the two hexagons in the mth set coinciding with the lowest corners of the pair of hexagons in the (m+1)th set. Each set has 1368 yods that are intrinsic to that set. The number of yods in the n sets ≡ N(n) = 1368n + 2. But

1368 = 1370 − 2 = 26 − 2 + 1344 = 24 + 1344.

∴ N(n) − 2 = 24n + 1344n.

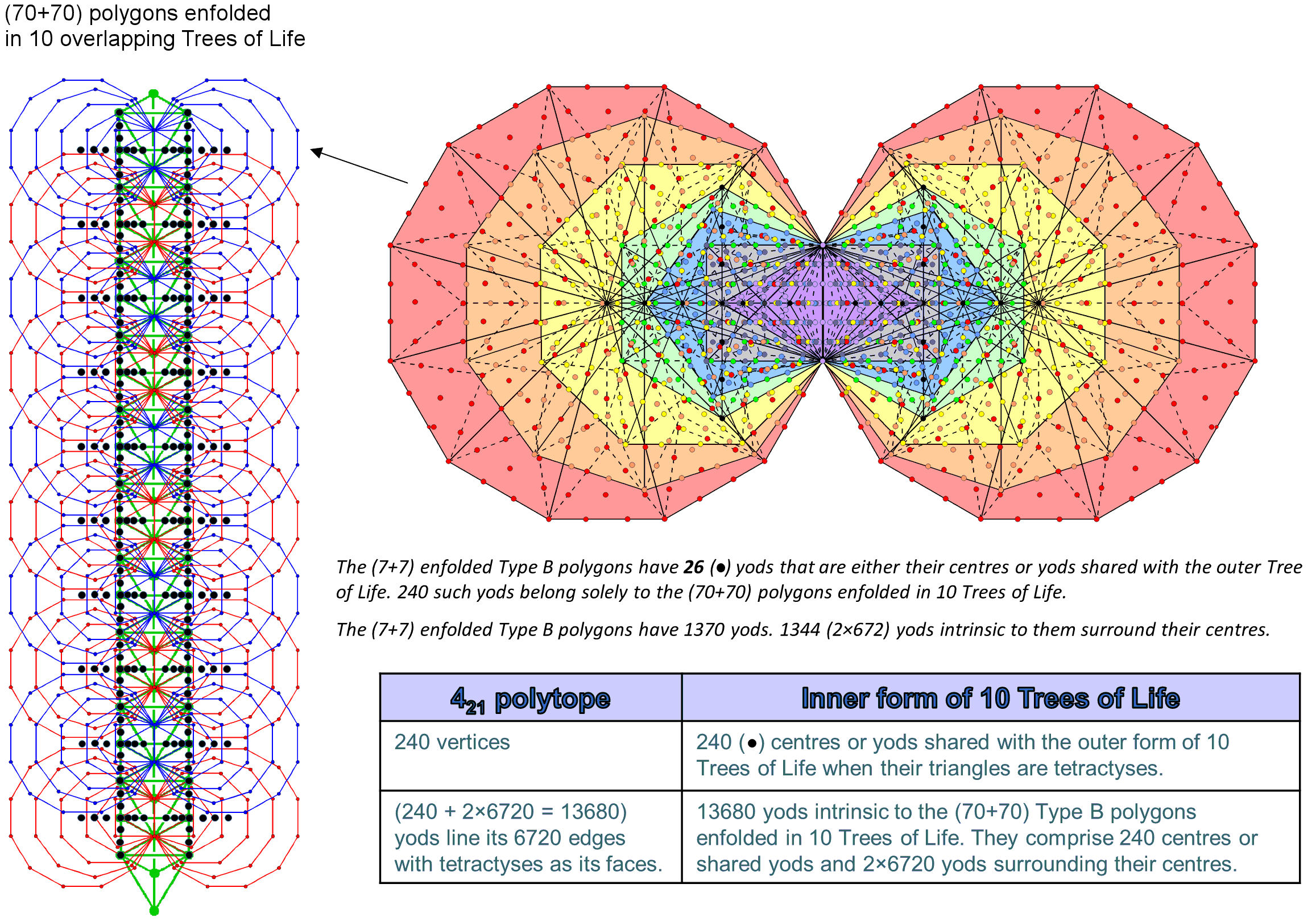
The number of yods intrinsic to the 10-tree = 240 + 13440 = 13680. The (70+70=140) polygons have 240 yods that are either shared with the 10 Trees of Life or centres of polygons that are not also corners. Surrounding the latter are 13440 yods that consist of 6720 pairs of yods. One yod in a pair belongs to a polygon in one set of 7 polygons and its partner belongs to the corresponding polygon in its mirror-image set.

Compare these properties of the inner form of 10 Trees of Life with the 4₂₁ polytope when it is constructed from tetractyses. It has 240 vertices that represent the 240 roots of the rank-8, exceptional Lie group E₈. Its 60480 triangular faces have 6720 edges. When each face is turned into a tetractys, two hexagonal yods line each edge. The number of yods lining the sides of the 60480 tetractyses = 240 + 6720×2 = 13680. This is the number of yods that are intrinsic to the inner form of 10 Trees of Life. The correspondences:

• 240 vertices → 240 shared yods or centres of (70+70) enfolded Type B polygons,
• 6720 pairs of hexagonal yods → 6720 pairs of yods,
• 13680 yods lining tetractyses → 13680 intrinsic yods in inner form of 10 Trees of Life,

have only one implication: the 4₂₁ polytope is the 8-dimensional realisation of the inner form of 10 Trees of Life. Because the 4₂₁ polytope possesses sacred geometry (see p. 2 et seq in the section 4-d sacred geometries), the symmetry group E₈ must be realised in Nature, so that E₈×E₈ heterotic superstrings must exist.

E₈ Coxeter plane projection of the 4₂₁ polytope.

The number of vertices in the 4₂₁ polytope = 240 = 2⁴ + 2⁵ + 2⁶ + 2⁷. As 240 = 16×15, where 16 = 4² and 15 = 4² − 1,

240 = 4²(4²−1) = 4⁴ − 4² = 2⁸ − 2⁴.

The number of edges in the 4₂₁ polytope = 6720 = 10×672. As 10 = 2¹ + 2³ and 672 = 2⁵ + 2⁷ + 2⁹,

6720 = 2⁶ + 2⁹ + 2¹¹ + 2¹².

The number of vertices & edges = 240 + 6720 = 6960 = 2⁴ + 2⁵ + 2⁸ + 2⁹ + 2¹¹ + 2¹².

The number of hexagonal yods lining the sides of the 60480 tetractyses in the 4₂₁ polytope = 2×6720 = 13440 = 2⁷ + 2¹⁰ + 2¹² + 2¹³.

The number of yods lining these sides = 240 + 13440 = 13680 = 2⁴ + 2⁵ + 2⁶ + 2⁸ + 2¹⁰ + 2¹² + 2¹³.

This is the number of yods intrinsic to the inner form of 10 Trees of Life, namely, the (70+70) Type B polygons (see discussion of previous diagram). Its power-of-2 expression is the sum of (4+4) powers of 2:

• 2⁴ + 2⁵ + 2⁶ + 2⁷ = 240 → 240 shared yods or centres of polygons → 240 vertices of the 4₂₁ polytope.
• 2⁷ + 2¹⁰ + 2¹² + 2¹³ = 13440 → 13440 unshared yods surrounding centres of polygons → 13440 hexagonal yods lining the 6720 sides of its 60480 tetractyses.

For more discussion of the yod composition of the 4₂₁ polytope, see here.