| << Previous 1... 6 7 [8] 9 10 Next >> |
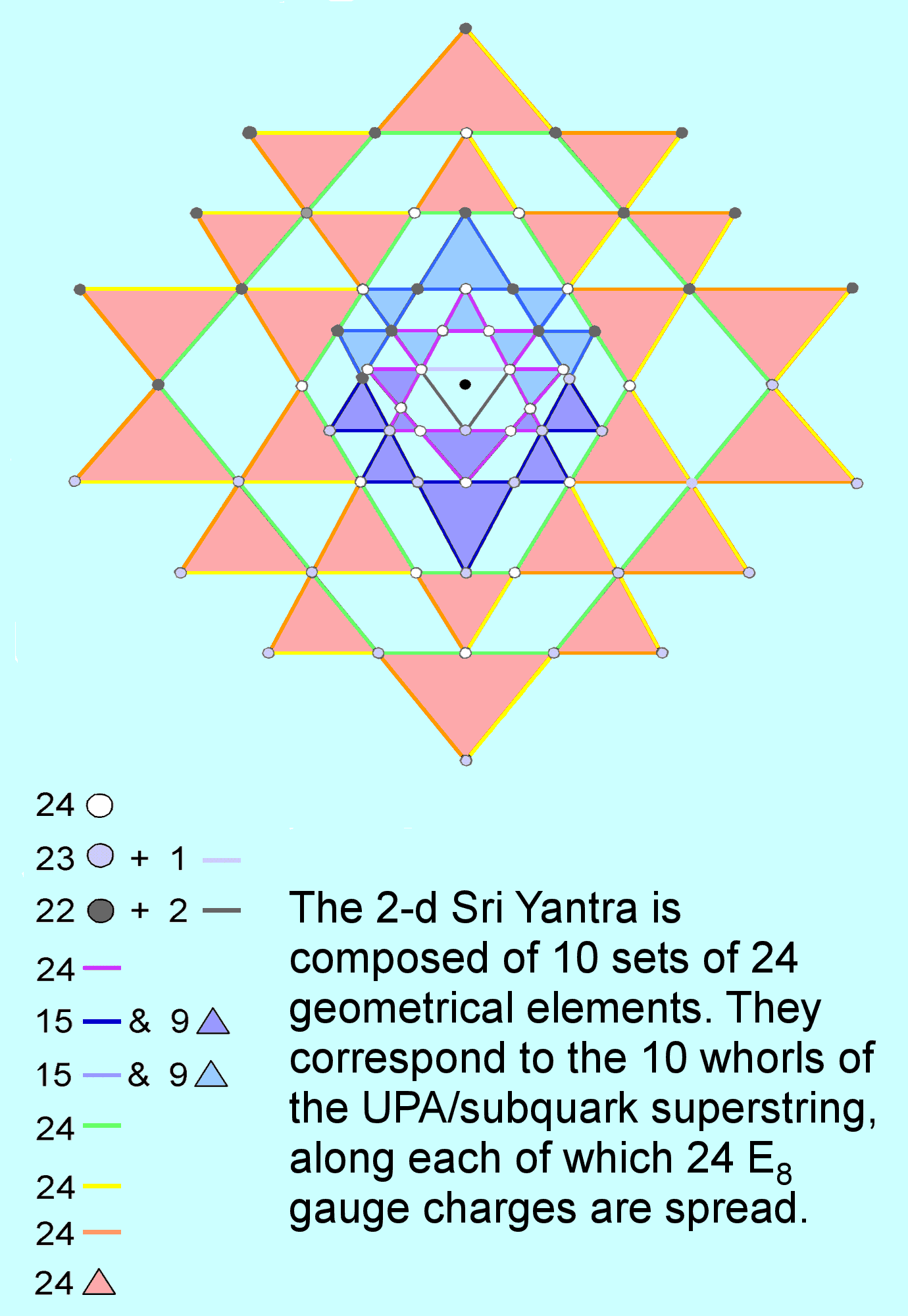
The ten-fold pattern of 240 geometrical elements surrounding the centre of the 2-d Sri Yantra

It was pointed out in #2 of this section that the 240 geometrical elements surrounding the centre of the 2-dimensional Sri Yantra comprise 72 points & lines and 168 lines & triangles. Their distribution is tabulated below:
| Number of corners |
Number of sides |
Number of triangles |
Total | |
| Central 'triangle' | 1 | 3 | 0 | 4 |
| 1st group of triangles (G1) |
4 + 8 = 12 |
8×3 = 24 |
8 |
44 |
| 2nd group of triangles (G2) |
6 + 10 = 16 |
10×3 = 30 |
10 |
56 |
| 3rd group of triangles (G3) |
2 + 10 = 12 |
10×3 = 30 |
10 |
52 |
| 4th group of triangles (G4) |
28 |
14×3 = 42 |
14 |
84 |
| Total |
69 |
129 |
42 |
240 |
Mathematically speaking, the central, downward-pointing triangle does not count as a true, triangular area (hence, the two inverted commas enclosing the word ‘triangle’ in the first row of the table and the '0' entry in the 'Number of triangles' column). This is because the bindu at the centre of the 2-dimensional Sri Yantra is a point that lies in its plane, so that what looks like a triangle is really only three lines and three points, the upper two of which coincide with corners of triangles that belong to the first group (G1). It is not a pure, triangular area. The metaphysical meaning of this central point not being just one of the points making up the surface of this illusory, central triangle is that it symbolizes the Absolute (Brahmin), the stage prior to the triple Godhead of Shiva, Brahma and Vishnu symbolized by the three corners of this triangle.
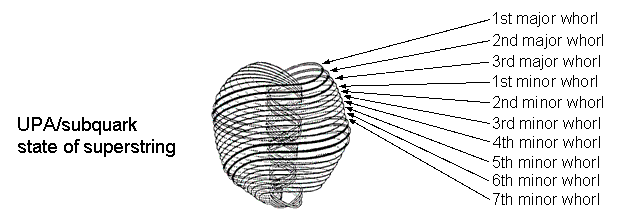
The Kabbalistic counterpart of the bindu would be the three Veils of Negative Existence: Ain (Absolute), Ain Soph (Limitless) & Ain Soph Aur (Limitless Light). The 42 triangles arranged around the centre of the 2-dimensional Sri Yantra have 126 sides, i.e., 168 lines & triangles surround it. Including the lowest corner of the central ‘triangle,’ the table indicates that 69 points surround this centre. Three straight lines form the boundary of this innermost 'triangle.' Hence, the 240 points, lines & triangles that surround the central bindu consist of (69+3=72) points & lines and 168 lines & triangles. This is the counterpart of the similar 72:168 division manifested by the two separate sets of seven enfolded polygons making up the inner Tree of Life (see here) and by the first three Platonic solids, which have 72 hexagonal yods in one half of the tetrahedron and the octahedron and 168 hexagonal yods in their other half and in the cube (see here). We shall see in the next section (see here) that it also appears in the disdyakis triacontahedron — the outer form of the polyhedral Tree of Life. It is the counterpart of the 72 roots of E6 and the remaining 168 roots of E8. Notice that the 168 lines & triangles comprise the 42 lines in G4 (the fourth group of triangles) and all 42 triangles, i.e., 84 lines & triangles, as well as 84 lines in the first three groups of triangles: G1, G2 & G3. Alternatively, the four groups of triangles in each half of the Sri Yantra comprise 63 sides and 21 triangles, i.e., 84 lines & triangles. This 84:84 division is characteristic of sacred geometries (see The holistic pattern). It manifests in the subquark state of the E8×E8 heterotic superstring as the 840 (=84×10) turns in an outer or inner half of each whorl of the UPA, that is, as the 84 turns in an outer or inner quarter-revolution of each whorl.
Groups G1 & G3 have (12+12=24) corners. The central ‘triangle’ comprises one unshared corner and three straight lines. They form two sets: one that is made up of this corner and the straight line opposite it and one that comprises the two lines that meet at this point. Groups G2 & G4 have (16+28=44) corners, i.e., 22 corners in each half of the Sri Yantra, making two sets of 22 corners. Combining them with the set of point & line and with the set of two lines creates two sets of 24 corners & sides. Hence, the 72 points & lines discussed in the previous paragraph divide into three sets of 24:
Set 1: G1 & G3 have 24 white corners;
Set 2: Central ‘triangle,’ G2 & G4 have 23 light grey corners & one light grey side;
Set 3: Central ‘triangle,’ G2 & G4 have 22 dark grey corners & two dark grey sides.
G3 has ten sets of three sides and G4 has 14 sets of three sides. Together, they form three sets of (10+14=24) sides and one set of (10+14=24) triangles. G1 & G2 have (8+10=18) triangles, i.e., nine in each half. G2 has 15 sides in each half. There are, therefore, (9+15=24) sides & triangles in each half of G1 and G2, as well as a set of 24 sides in the former group. The 168 sides & triangles in the four groups of triangles divide into seven sets of 24:
Set 4: G1 has 24 violet sides;
Set 5: G1 & G2 have 24 sides & triangles(15 indigo sides & 9 indigo triangles) in one half of the Sri Yantra;
Set 6: G1 & G2 have 24 sides & triangles (15 blue sides & 9 blue triangles) in other half of the Sri Yantra;
Set 7: G3 & G4 have set of 24 green sides;
Set 8: G3 & G4 have set of 24 orange sides;
Set 9: G3 & G4 have set of 24 yellow sides;
Set 10: G3 & G4 have set of 24 red triangles.
In conclusion, the 240 geometrical elements surrounding the bindu point at the centre of the 2-dimensional Sri Yantra consist of 10 sets of 24 elements that divide into three sets of points & lines and into seven sets of lines & triangles. They are the counterpart of the three major whorls and seven minor whorls of the UPA/subquark, along each of which 24 E8 gauge charges are spread. This is the microscopic manifestation of the (3+7=10) Sephiroth of the Tree of Life. Set 1 consist of points, that is, the most basic type of geometrical element. They fulfill the function of Kether, which, being the first Sephirah, is symbolized by a point. Sets 2 and 3 correspond, respectively, to Chokmah and Binah. Set 4 consists of the 24 violet sides of the eight triangles in G1; it corresponds to Chesed, the first Sephirah of Construction. Set 5, consisting of the 15 indigo sides & nine indigo triangles in G1 and G2 in one half of the Sri Yantra, corresponds to Geburah. Set 6, the counterpart of Set 5 in the other half, consists of 15 blue sides & nine blue triangles and corresponds to Tiphareth. Set 7 comprises the 24 green sides of the G3 & G4 triangles and corresponds to Netzach. Set 8 comprises the 24 yellow sides of the G3 & G4 triangles and corresponds to Hod. Set 9 comprises the 24 orange sides of the G3 & G4 triangles and corresponds to Yesod. Finally, set 10 comprises the 24 red triangles of G3 & G4 and corresponds to Malkuth.
Question: how could such a natural 10-fold division of the 240 geometrical elements of the 2-dimensional Sri Yantra exist unless this famous yantra is, indeed, the cosmic blueprint — one among several isomorphic representations of it analysed in this website — one of whose defining parameters manifests in the subatomic world as the 240 E8 gauge charges carried by the E8×E8 heterotic superstring? The sceptic will want to argue that the analysis presented above has no significant implication because it has been concocted in order to generate such a 10-fold division. But this objection begs the question that an orderly pattern of selection of 10 sets of geometrical elements would always be possible if the Sri Yantra were merely a jumble of points, lines & triangles without any fundamental meaning whatsoever in its apparent design. Obviously, any set of 240 geometrical elements can always be divided up into 10 sets of 24 elements if their selection is purely random. But the pattern of division displayed above is not random but highly coherent, displaying an intrinsic, natural order — not the kind of incongruous combinations that would be generated by an arbitrary picking of 10 sets of elements! This feature is inconsistent with the sceptic's criticism, which has to be refuted because it cannot account for the simple, uncontrived order displayed in the selection of sets 1-10 shown above. Such a pattern of order cannot be concocted from a chaotic collection of geometrical elements that has no underlying, conceptual coherence.