| << Previous 1... 5 6 [7] 8 9 ...10 Next >> |
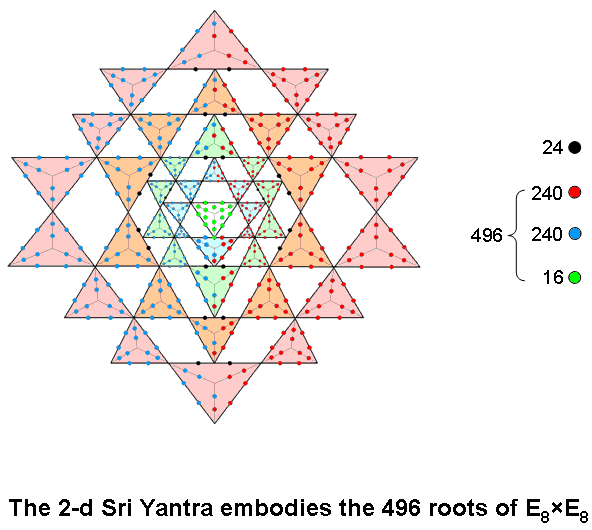
How the 2-d Sri Yantra embodies the 496 roots of E8×E8 and SO(32)

According to Table 8 in Article 35, when its 43 triangles are transformed into Type A triangles, the two-dimensional Sri Yantra contains 757 yods. 756 yods surround the bindu point. Of these, 16 green yods belong solely to the central triangle (its two upper corners are also corners of the innermost set of eight triangles, so that green yods are not assigned to them). According to this table, 504 hexagonal yods line the 252 sides of the 126 tetractyses in the 42 triangles surrounding the central one. The tips of some of these triangles touch twelve of their sides. From a strict, mathematical point of view, these particular sides are not single, straight lines but pairs of lines joined at the tip of another triangle. This leaves (252–12=240) true sides (i.e., single, straight lines) with 480 hexagonal yods. These yods cannot be divided into two sets of 240 that are mirror images of one another, if the mirror is horizontal, because three of the four sides excluded from the layer of ten blue triangles in Figure 1 of Article 35 (or see here) belong solely to its upper half, creating an imbalance. However, a mirror symmetry persists after excluding the 12 sides if the mirror is vertical, for, then, 240 red hexagonal yods and 240 blue hexagonal yods lie either on or, respectively, to the right and left of the vertical axis passing through the centre of the central triangle, which is surrounded by (240+240+16=496) yods on true sides.
The 24 hexagonal yods lining sides that are touched by other true triangles are coloured black. The two hexagonal yods in the side of the triangle touched by the lowest corner of the central triangle are not black because, although it has the appearance of a triangle, the central triangle, mathematically speaking, does not constitute a true, triangular area, the bindu (a separate point) coinciding with its centre. In the 3-dimensional Sri Yantra, the central triangle really is a triangle because the bindu hovers above it instead of being embedded in its surface. If it were traversed by various lines, it would be obvious that this "triangle" could not be regarded as a pure triangle. To the mathematical novice, it is not as obvious that it loses this status when merely the bindu is embedded in its surface. But the principle remains the same even if it is divided into its sectors. The 16 green yods that surround the bindu are intrinsic to this Type A triangle because they are unshared with any of the 42 triangles that are around it. They symbolize the 16 simple roots of E8×E8 (see here). The (240+240=480) hexagonal yods on the 240 single lines making up the true sides of the 42 triangles denote its (240+240=480) roots. Without the axial symmetry of the Sri Yantra, the 496 yods could not be divided into two similar sets of 248 yods. Instead, the Sri Yantra would embody the 496 roots of SO(32), the second Lie group with the dimension 496 that governs Type 1 open and closed superstrings and the second type of closed heterotic superstrings. It is as if the two possible gauge symmetry groups governing superstring forces allowed by superstring theory correspond to the two orthogonal orientations of the Sri Yantra, its traditional one (E8×E8) displaying a left/right mirror symmetry and the other one rotated by 90° (SO(32)) not doing so:
.gif)
The 72:168 division characteristic of holistic systems manifests in each half of the 2-dimensional Sri Yantra composed of Type A triangles as the (6×12=72) hexagonal yods in the six red triangles on each side of its central axis and as the 168 hexagonal yods in the remaining 19 triangles. E6, the exceptional subgroup of E8, has 78 roots that comprise six simple roots symbolized by the six green yods in the central triangle that are on either side of the vertical mirror plane and 72 roots denoted by these 72 red or blue hexagonal yods.
As supporting evidence that this is the correct way of seeing how the number 496 at the heart of superstring theory is embodied in the two-dimensional Sri Yantra, it was pointed out here that this sacred geometrical object is composed of 240 geometrical elements (69 points, 129 lines & 42 triangles) surrounding its centre when all triangles are not divided into their sectors. In other words, including the centre, there are (241–12=229) true elements when the 12 sides touched by triangles are left out of consideration as single lines. 229 is the 50th prime number, showing how ELOHIM with number value 50 prescribes the true, geometrical composition of this sacred geometry. There are 70 points and (129−12=117) true sides, i.e., 187 true points & lines, where 187 is the number value of Auphanim, the Order of Angels assigned to Chokmah. There are (70+42=112) points & triangles, where 112 is the number value of Beni Elohim, the Order of Angels assigned to Hod.