
| << Previous 1... 28 29 [30] 31 32 ...50 Next >> |

As pointed out on page 13, the 240 roots of the Lie group E8 can be regarded as consisting of the 72 roots of its exceptional subgroup E6 and 168 other roots. When their 47 sectors are tetractyses, the seven enfolded polygons of the inner Tree of Life have 120 yods on their 42 sides, where
120 = 22 + 42 + 62 + 82.
They comprise 36 (=62) black yods at the corners of polygons and 84 (=22+42+82) red hexagonal yods. The two separate sets of seven enfolded polygons have (2×36=72) black yods at their corners and (2×84=168) red hexagonal yods. The distinction between corners and hexagonal yods corresponds to E6 being a subgroup of E8. This is the sacred geometrical counterpart of the symmetry-breakdown of E8 into E6 that has been considered by superstring theorists in order to reproduce the physics of the Standard Model. Each yod on the boundaries of the polygons symbolizes a root of E8 to which correspond a gauge charge and a gauge boson mediating the unified force between superstrings.
The 10-fold UPA/superstring as the 10-fold division of the (7+7)
polygons
E6 contains the exceptional subgroup F4 with dimension 52. It has four simple roots and 48 roots. As the first six enfolded polygons have 24 corners outside their shared root edge, the counterpart of the 48 roots in the inner Tree of Life are the (24+24=48) black yods at the corners of the two sets of the first (6+6) enfolded polygons that are outside their root edges. The two separate dodecagons have (12+12=24) corners. We see that the 72 corners divide naturally into three groups of 24 corners. Do the 168 red hexagonal yods also split up naturally into seven groups of 24? Indeed, they do! Below are shown the numbers of hexagonal yods on the sides of one set of seven enfolded polygons:
| triangle |
square |
pentagon | hexagon | octagon | decagon | dodecagon |
| 4 | 6 | 8 | 10 | 14 | 18 | 24 |
(the root edge must be associated with the dodecagon because it then generates its 24 hexagonal yods). The 18 hexagonal yods on the sides of the decagon can only be grouped with the six hexagonal yods of the square in order to form a set of 24, the 14 hexagonal yods of the octagon can only be grouped with the ten hexagonal yods of the hexagon and the eight hexagonal yods of the pentagon can only be grouped with the four hexagonal yods of the remaining triangle to generate 24 hexagonal yods in both sets. Hence, there are two sets of 24 (dodecagons), two sets of 24 (decagon & square), two sets of 24 (octagon & hexagon) and one set of 24 (triangle & pentagon). No other combinations are possible. Amazingly, both the 72 corners and 168 hexagonal yods group naturally into ten sets of 24 yods (they are coloured black, white, grey and the seven colours of the rainbow in the diagram below). The significance of this for superstrings is as follows: in some of his research articles on this website, the author identified the UPA described by Besant & Leadbeater as the subquark state of the E8×E8 heterotic superstring. In the limit of exact E8 symmetry, its ten whorls "carry" the 240 gauge charges of E8 corresponding to its 240 roots. In the spirit of heterotic string theory, 24 gauge
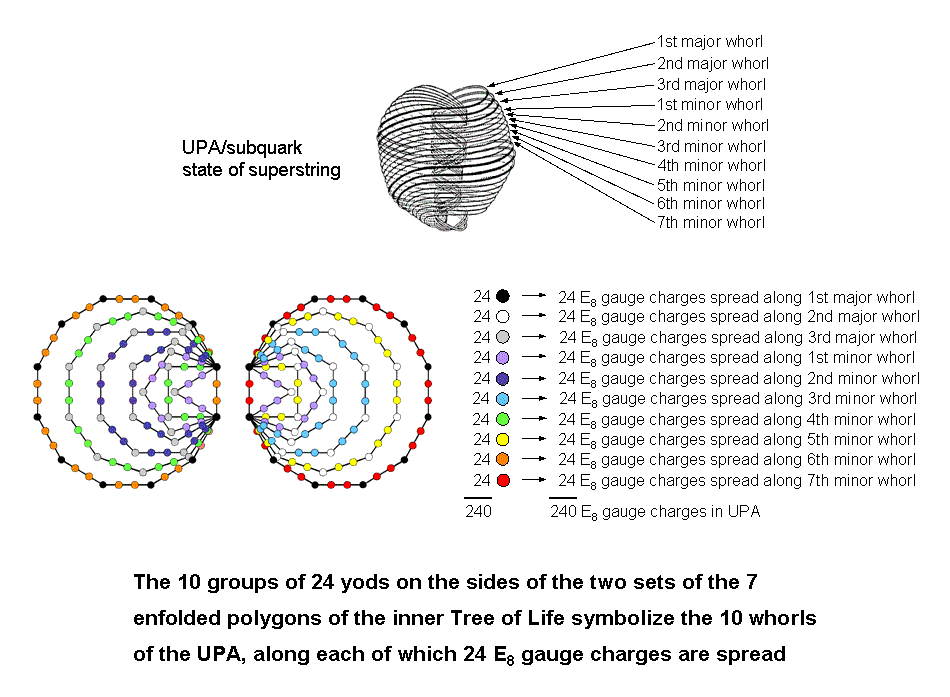
 charges are spread out along each whorl. The three major whorls carry
72 gauge charges and the seven minor whorls carry 168 gauge
charges. This 72:168 division is precisely what we see in the
distinction between the 72 corners and the 168 hexagonal yods on
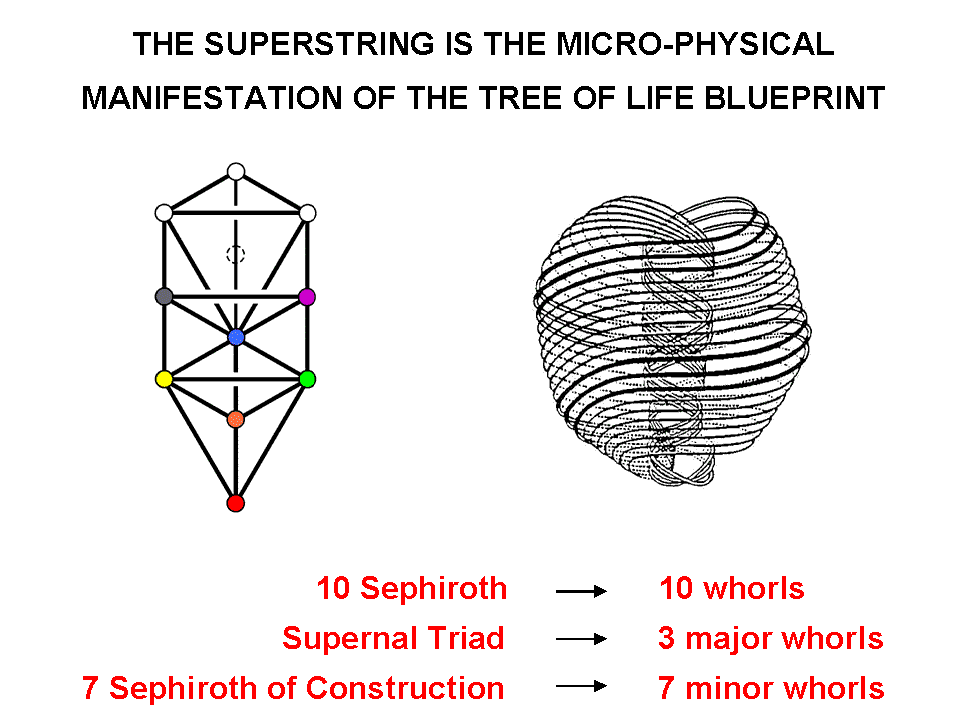
the sides of the two sets of the seven enfolded polygons. The corners perform the role of the three major
whorls, which are the micro-physical manifestation of the three Sephiroth of the Supernal Triad, and the
hexagonal yods have the role of the seven minor whorls, which are the micro-physical manifestation of the
seven Sephiroth of Construction. Remarkably, this analogy extends even to the individual whorls,
for the ten sets of 24 gauge charges of E8 carried by the 10 whorls correspond to the ten
groups of corners and hexagonal yods.
charges are spread out along each whorl. The three major whorls carry
72 gauge charges and the seven minor whorls carry 168 gauge
charges. This 72:168 division is precisely what we see in the
distinction between the 72 corners and the 168 hexagonal yods on
the sides of the two sets of the seven enfolded polygons. The corners perform the role of the three major
whorls, which are the micro-physical manifestation of the three Sephiroth of the Supernal Triad, and the
hexagonal yods have the role of the seven minor whorls, which are the micro-physical manifestation of the
seven Sephiroth of Construction. Remarkably, this analogy extends even to the individual whorls,
for the ten sets of 24 gauge charges of E8 carried by the 10 whorls correspond to the ten
groups of corners and hexagonal yods.
The counterpart in the first six enfolded polygons (which constitute a holistic set in themselves) of each set of 24 gauge charges are the 24 intrinsic corners associated* with them. The 60 polygons enfolded in ten overlapping Trees, each mapping a whorl, have 240 associated corners that correspond to the 240 roots of E8 and their associated gauge charges. The (240+240) intrinsic corners associated with both sets of 60 polygons enfolded in ten overlapping Trees of Life denote the (240+240=480) roots of E8×E8, i.e., the mirror symmetry of the inner Tree of Life is responsible for the direct product nature of the anomaly-free gauge symmetry group for the unified force between E8×E8 heterotic superstrings.
|
|
The (240+240) intrinsic corners of the first (6+6) polygons enfolded in 10 overlapping Trees of Life denote the (240+240) roots of E8×E8. Each Tree maps a dimension of the 10-dimensional space-time of superstrings. |
As
|
3 |
||||
| 5 | 7 | |||
|
112 − 1 = 120 = |
9 |
11 |
13 |
|
| 15 | 17 | 19 | 21 . |
i.e., as 120 is the sum of the first ten odd integers after 1, the number 240 is the sum of the ten even integers that start with 6 and are four units apart:
|
6 |
||||
|
10 |
14 |
|||
|
240 = |
18 |
22 |
26 |
|
|
30 |
34 |
38 |
42 . |
In terms of the numbers 1, 2, 3 & 4 symbolized by the four rows of dots in the tetractys, this number is 1×2×3×4(1+2+3+4).
As 52 − 1 = 24 = 3 + 5 + 7 + 9, the number 240 is the sum of the tetractys arrays of the first four odd integers after 1:
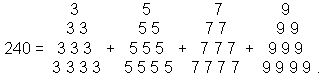
The sum of the 12 odd integers at the corners of these tetractyses is 72 and the sum of the remaining 28 odd integers is 168. This is the arithmetic counterpart of the 72 corners and 168 hexagonal yods that line the two separate sets of the seven enfolded polygons. A beautiful harmony always exists between number and geometry when the latter is sacred. As we found on page 28, the number 16800 — the number of 1st-order spirillae in the UPA — is the sum of 240 odd integers.
For further discussion of the 10-fold division of the inner Tree of Life and how it represents the ten whorls of the UPA/subquark superstring, see Article 53.
* The two endpoints of the root edge are shared by both sets of seven polygons. One can be associated with one set and one with the other set. The topmost corner of the hexagon coincides with the lowest corner of the hexagon enfolded in the next higher Tree. Both sets of the first six polygons have 50 corners. 25 corners are associated with each set but only 24 of these belong exclusively to that set in the sense of being unshared with polygons enfolded in the next higher Tree and are therefore intrinsic to it.
| << Previous 1... 28 29 [30] 31 32 ...50 Next >> |