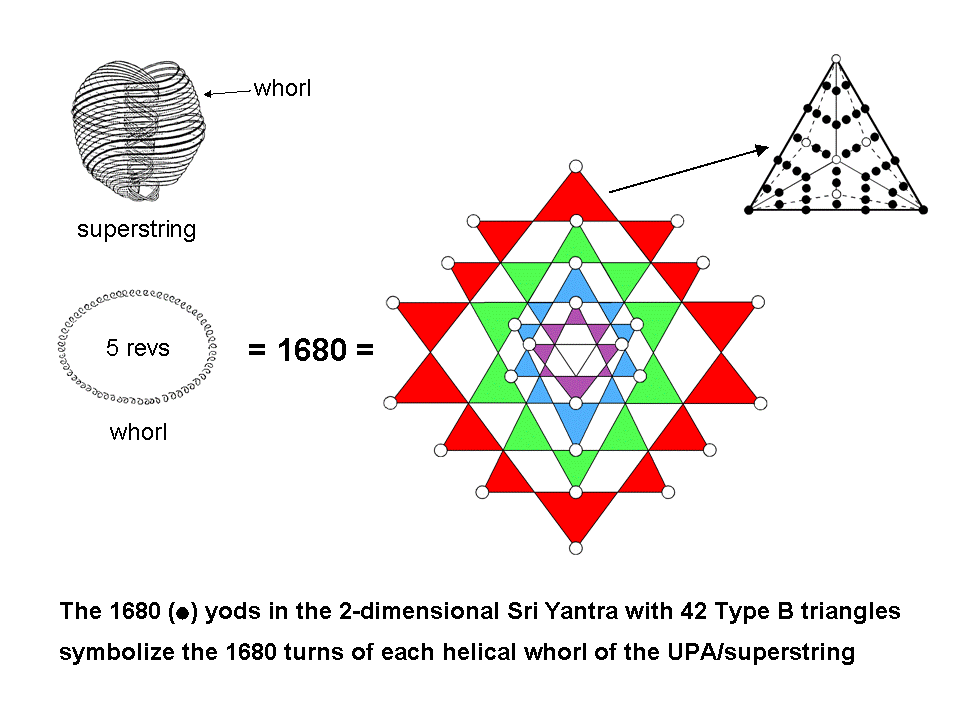
1680 embodied in 2-d Sri Yantra
Suppose that we regard the triangles of the 3-dimensional Sri Yantra as Type B triangles, each sector being further divided into three sectors, each of which is a tetractys, generating 46 yods. As one corner of a triangle is shared with the next triangle in the same layer, the 42 triangles have (42×45=1890) yods. As 16 corners coincide with corners of triangles in adjacent layers when the four layers merge into the 2-dimensional Sri Yantra, the 42 Type B triangles in the latter have (1890–16=1874) yods. Their 378 tetractyses have (42×4=168) corners (white circles) within the 42 triangles, which have (1874–168=1706) yods other than these. They comprise 26 tips of the nine primary triangles (denoted by the larger white circles). There are, therefore, (1706–26=1680) new yods generated by the intersection of these primary triangles that are not corners of tetractyses inside the Type B triangles. Each yod symbolizes one of the 1680 turns of the helical whorl of the UPA/superstring. The Godname YAHWEH with number value 26 prescribes not only the dimensionality of the 26-dimensional space-time of bosonic strings in which certain modes of vibration of the E₈×E₈ heterotic superstring occur but also how many circularly polarised oscillations take place in each of its helical whorls. Notice that the 26 original corners form 13 pairs that are diametrically opposite each other (see #5). This means that the 1680 new yods consist of 840 pairs of yods that are in opposite sides of the Sri Yantra. This is consistent with how each helical whorl of the UPA/ subquark superstring divides into 840 turns in its outer 2½ revolutions around the spin axis of the particle and the 840 turns in its inner 2½ revolutions about this axis.

1680 embodied in 3-d Sri Yantra
Of the 46 yods in a Type B triangle, five unshared yods per triangle line its outer two sides when it is part of the 3-dimensional Sri Yantra. This is not the case for the 2-dimensional Sri Yantra because some corners of 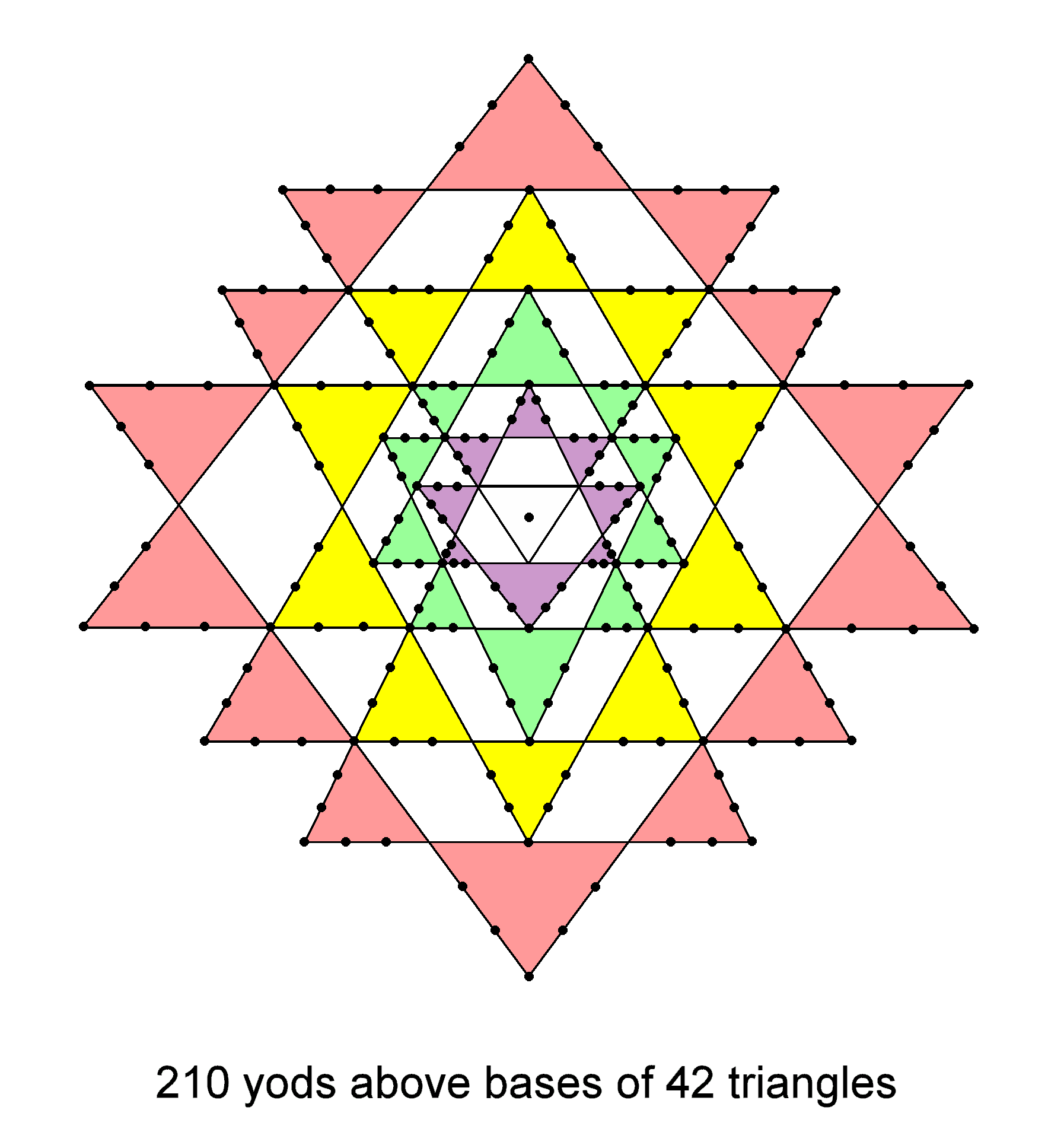triangles coincide with corners of triangles in what in the 3-d case are other layers. Therefore, each triangle has 41 yods (40 yods per triangle) not forming the spiky, outer perimeter of the 3-d Sri Yantra. (5×42=210=21×10) yods made up of 168 hexagonal yods & 42 corners line the 84 outer sides of the 42 triangles above their bases, creating their points, and (42×40=1680) yods are within the perimeter delineated by these 210 yods, 840 yods being in each half of the Sri Yantra. What this means is that, given the jagged outline of a Sri Yantra showing just points of triangles, each marked by five yods, not triangles with a third side, 1680 new yods are needed to create the 42 Type B triangles. This is consistent with how this number shapes a helical whorl of the UPA/superstring constituent of quarks.

Sixteen of the 210 yods are corners that coincide with corners of triangles in adjacent layers when the Sri Yantra becomes 2-dimensional, leaving 194 yods. 194 is the number value of Tzadekh, the Mundane Chakra of Chesed. Of these, 26 are corners and 168 are hexagonal yods.

Of the 336 yods on the boundaries of the 42 triangles of the 3-dimensional Sri Yantra, 26 yods are corners of the nine parent triangles, leaving 310 (=31×10) generated yods. This shows how the Godname EL of Chesed with number value 31 prescribes the geometry of the Sri Yantra that embodies the superstring structural parameter 1680. Chesed is directly below Chokmah with Godname YAHWEH on the Pillar of Mercy of the Tree of Life. Both EL and YAHWEH prescribe the superstring structural parameter 336: 336 = 26 + 31×10. 155 new yods delineate the boundary of each half, demonstrating how ADONAI MELEKH, the complete Godname of Malkuth with number value 155, prescribes, in conformity to the meaning of this Sephirah, the physical shape of each of the ten whorls, which are the Malkuth aspect of the 10-fold, microscopic Tree of Life quantified by the number value 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth. ADONAI MELEKH has the pentagramic representation:

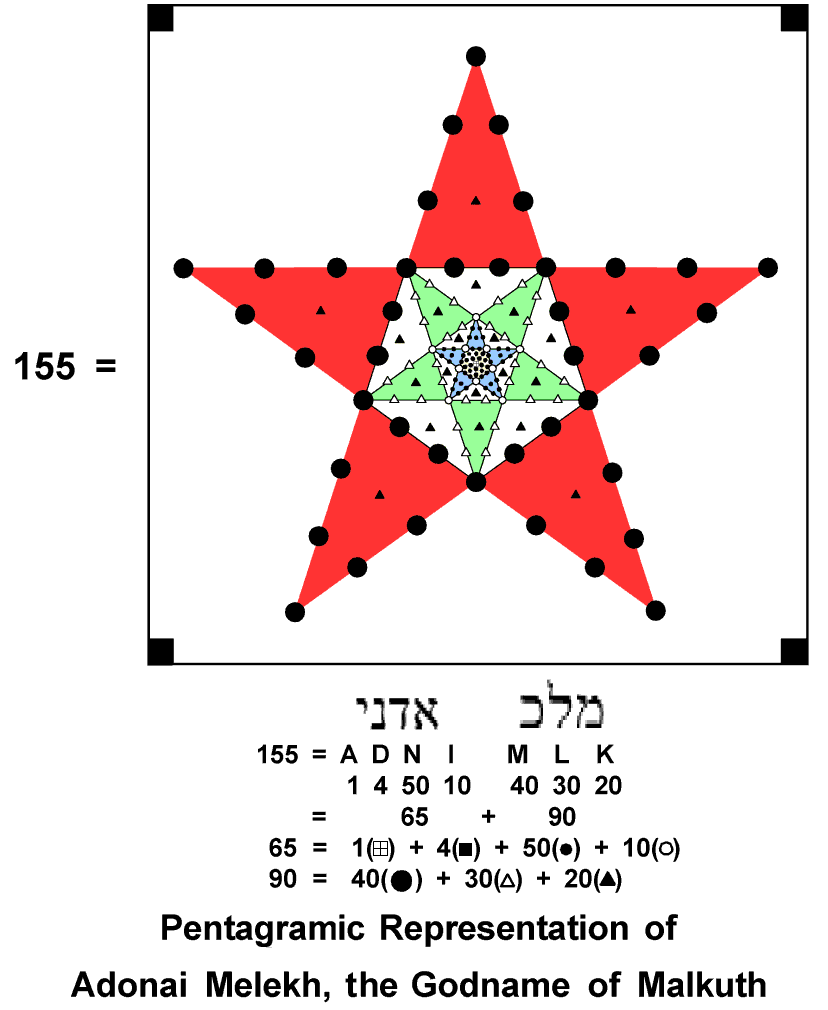
The letter values of the complete Godname of Malkuth denote the numbers of various classes of yods. The arithmetic sum:

168 = 13 + 155

expresses the fact that the 168 yods on the boundary of each half of the 3-dimensional Sri Yantra consist of 13 corners of its nine parent triangles and 155 generated yods:

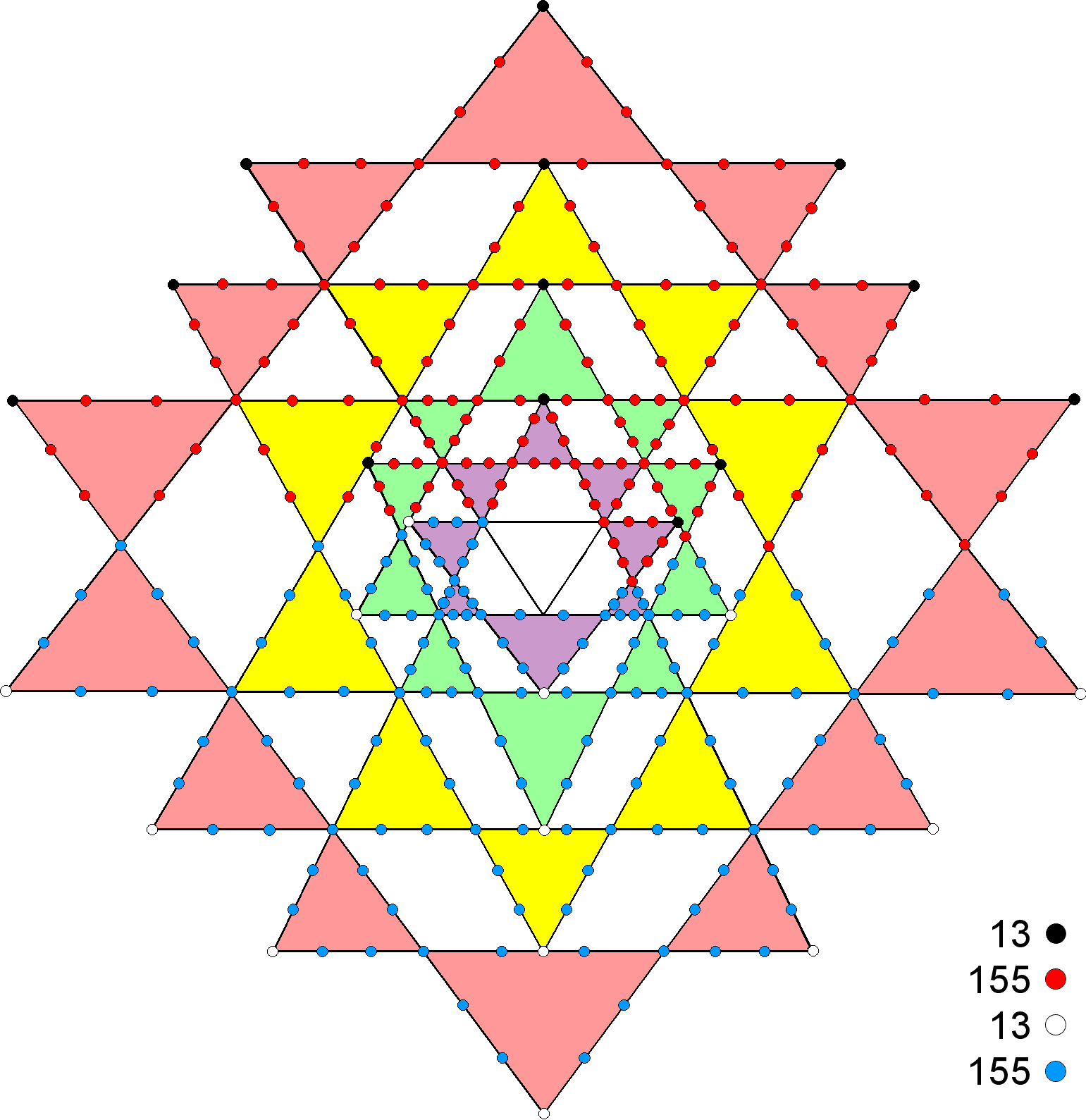168 yods comprising 13 black/white corners of the 9 parent triangles and 155 red/blue yods line the 63 sides of the 21 triangles in each half of the 3-d Sri Yantra when they are turned into tetractyses. The Godname ADONAI MELEKH with the number value 155 measures how many more yods are needed to delineate each half of the Sri Yantra. The central bindu and the hexagonal yods at the centres of the triangles are omitted for the sake of clarity.

Here is a remarkable, geometrically-based conjunction of the gematria numbers of the complete Godname (155) and Mundane Chakra (168) of the same Sephirah. Needless to say, it is not plausible that this might be fortuitous.

The counterpart of this 13:155 division of the superstring structural parameter 168 in the two joined Type B dodecagons of the inner Tree of Life is as follows: each Type dodecagon contains 181 yods. Joined at their root edge, two such dodecagons contain 358 yods, of which 22 yods are their corners. Hence, (358−22=336) more yods are needed to turn them into Type B dodecagons. Two of these yods lie on the root edge. One is associated with one dodecagon and the other is associated with the second dodecagon. The 168 yods associated with each dodecagon consist of 13 black or white corners of 36 tetractyses and 155 red or blue hexagonal yods:

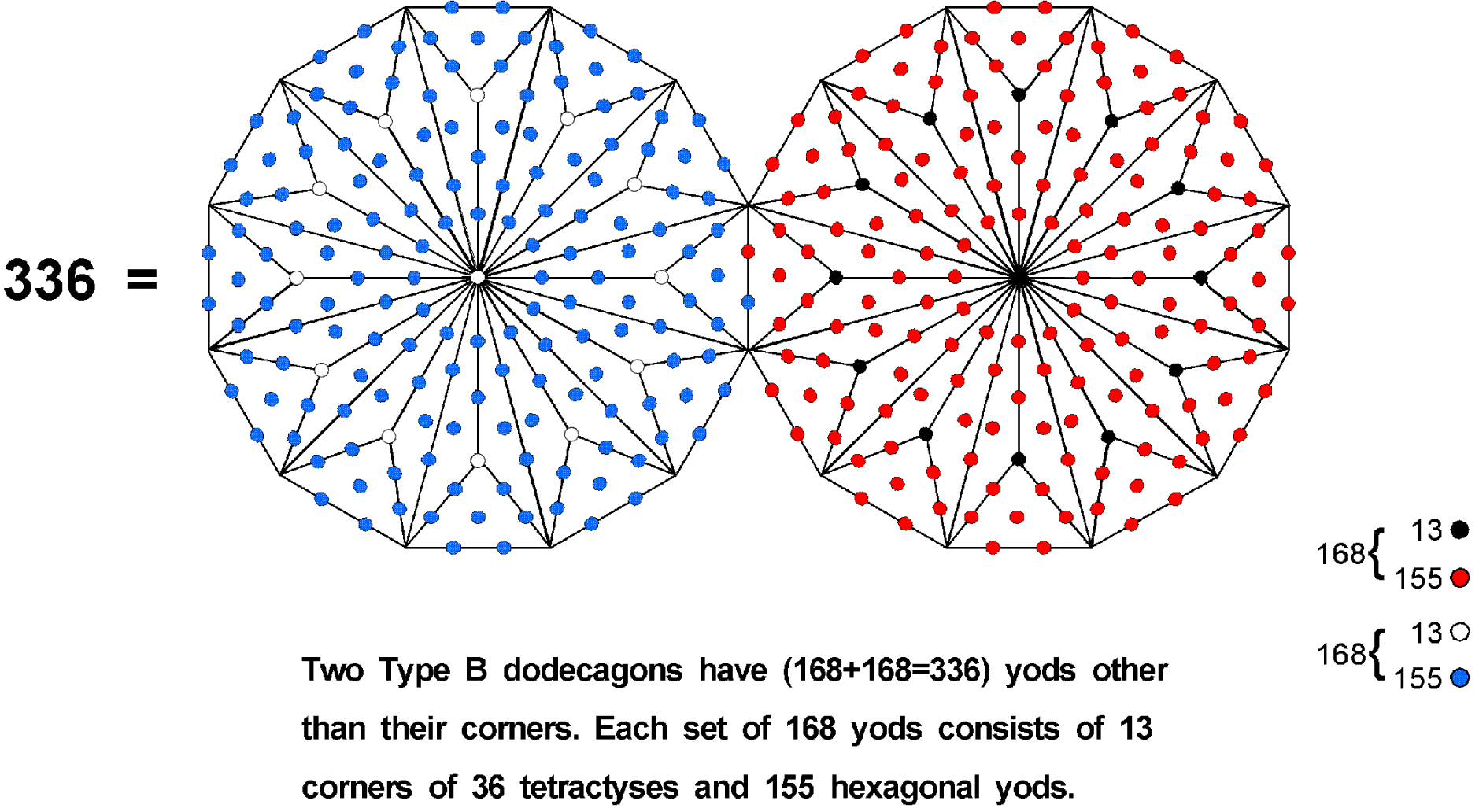
This correspondence is evidence supplementing that discussed elsewhere in this website that the pair of dodecagons constitutes a holistic system in its own right, embodying the patterns and parameters that are characteristic of such systems.

<< Previous    1...   4  5  [6]  7  8  ...10    Next >>

Home