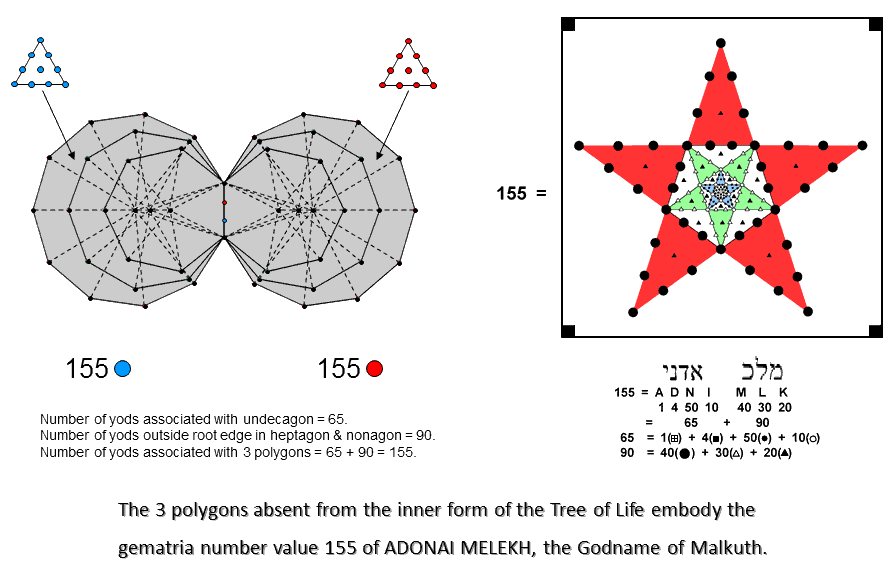
According to Table 2, the 3 enfolded Type A polygons have 157 yods. Two yods in the root edge can be associated with each set of 3 enfolded Type A polygons. (157−2=155) yods can be associated with each set of enfolded polygons. 155 is the number value of ADONAI MELEKH, the complete Godname of Malkuth. The number value 65 of ADONAI is the number of yods associated with the undecagon. The number value 90 of MELEKH is the number of yods outside the root edge in the heptagon and nonagon.

Compare this with the pentagramic representation of this Godname. The 4 corners of the enclosing square (denoted by black squares) correspond to the 4 yods in the root edge.

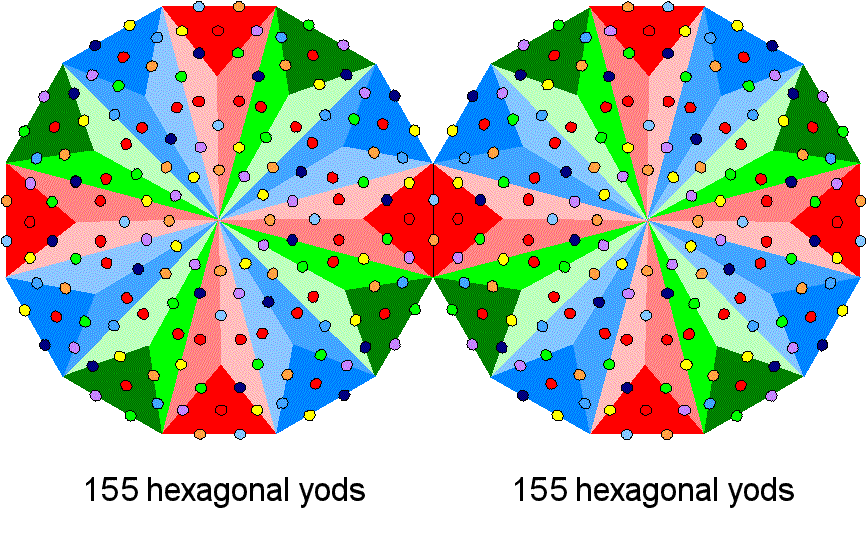
The dodecagon is the last of the 7 types of regular polygons that make up the inner form of the Tree of Life. Amazingly, the 155:155 division that exists in the 3 polygons absent from the inner Tree of Life re-appears in the two Type B dodecagons that complete it because there are 155 hexagonal yods associated with each dodecagon.* Within the Godhead, a 7-fold development takes place that, in terms of its geometrical analogy, ends with the 10th regular polygon — the dodecagon. As discussed in later pages, this polygon embodies the superstring structural parameters 168 and 336, the former being also the gematria number value of Cholem Yesodoth, the Mundane Chakra of Malkuth.

* Proof: according to Table 1, the number of hexagonal yods in the nth-order N-gon ≡ h_n^N = (4×3ⁿ⁻¹ + 1)N. For the Type B dodecagon, n = 2 & N = 12, so that h₂¹² = 13×12 = 156. Therefore, 155 hexagonal yods are associated with each Type B dodecagon joined at the root edge.