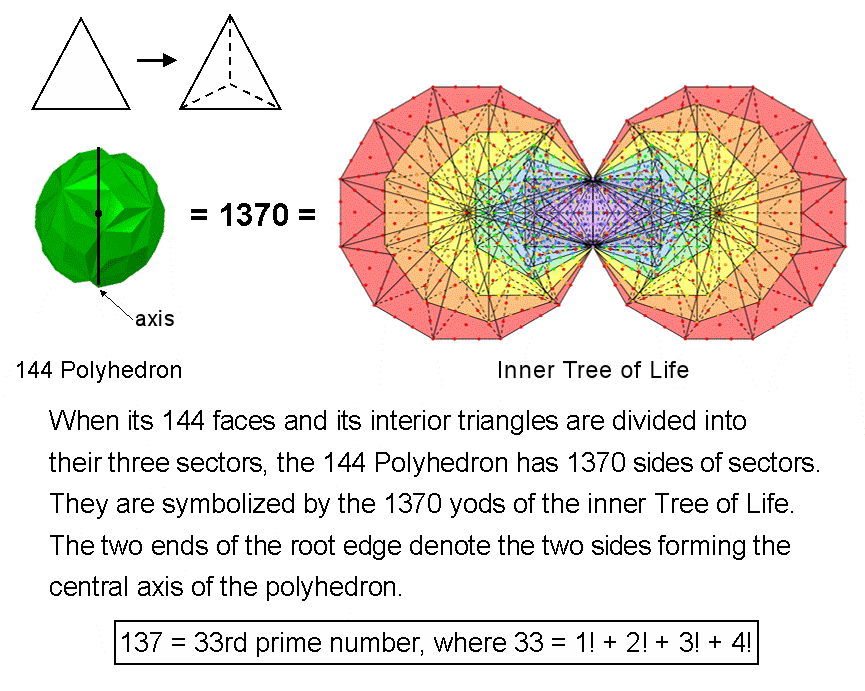
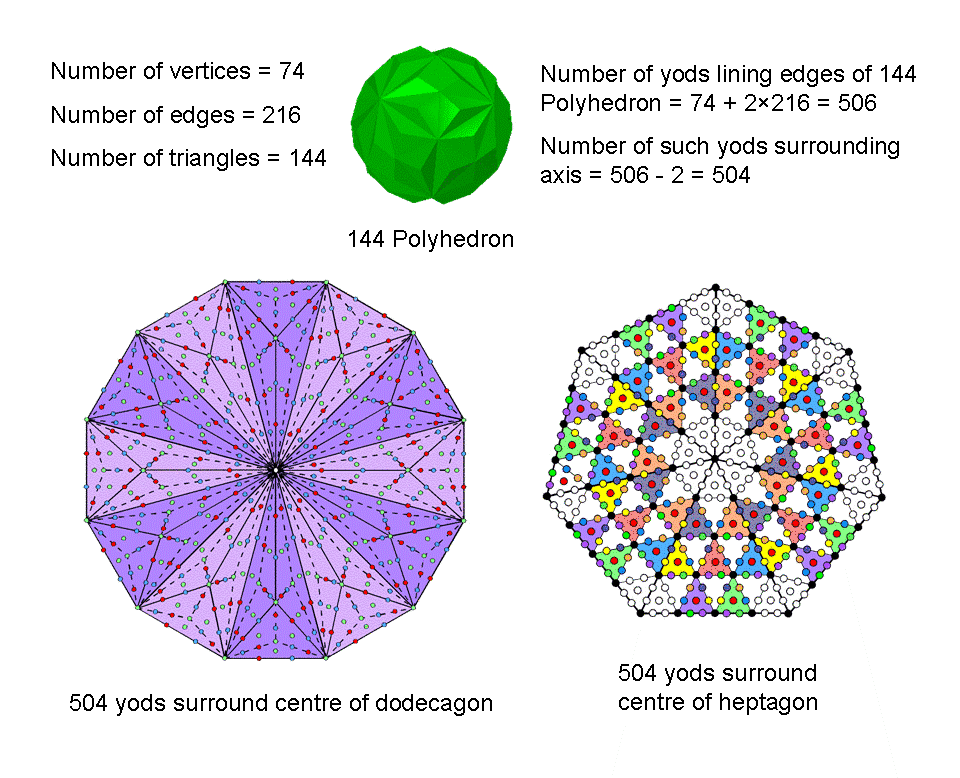
#7 The 144 Polyhedron

Suppose that the 144 triangular faces of the 144 Polyhedron with 216 edges are divided into their sectors, i.e., they are regarded as Type A triangles. This creates (3×144=432) triangles in its faces with 432 internal sides and 216 external sides, that is, 648 sides. Next, suppose that the 216 internal triangles formed by joining the centre of the 144 Polyhedron to its 74 vertices are divided into their (3×216=648) sectors with 648 internal sides. The 74 vertices are the endpoints of 74 sides of internal triangles, so that, inside the 144 Polyhedron, there are (648+74=722) sides of 648 triangles, including the two sides that form an axis joining any two diametrically opposite vertices. The (432+648=1080) triangles making up the 144 Polyhedron have (648+722=1370) sides. This is the number of yods in the 14 enfolded polygons of the inner Tree of Life when their 94 sectors are Type A triangles! It is remarkable evidence that the 144 Polyhedron is a holistic object that embodies the global properties of the inner Tree of Life, each yod symbolising a side of its 1080 triangles. The 74 sides of the 216 internal triangles correspond to the 74 corners of the 94 sectors of the (7+7) enfolded polygons that are not corners of triangles belonging to the outer Tree of Life, i.e, unshared yods. The 648 sides of the 432 triangles in the 144 faces and the 648 sides inside internal triangles formed by edges correspond to the remaining 648 yods in each half of the inner Tree of Life with Type B polygons.

The axis of the 144 Polyhedron consists of two sides of internal triangles. Surrounding them are 72 more such sides. Their counterpart in the inner Tree of Life are the 72 unshared corners of sectors that are outside the root edge. The number of Chesed is 72. The total number of sides surrounding the axis = 1368 = 37² − 1 = 3 + 5 + 7 +... + 73, i.e., the sum of the first 36 odd integers after 1. This number can be represented by assigning these integers to the sides of a Star of David or a hexagram, four per side: 

1368 =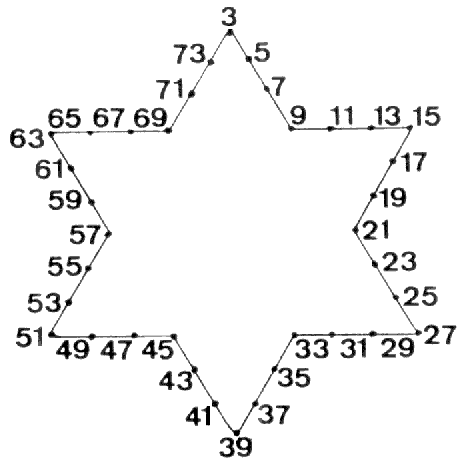

Curiously, the 74 vertices of the 144 Polyhedron consist of 37 pairs of diametrically opposite vertices. The two Type A hexagons in the inner form of the Tree of Life each has 37 yods that symbolise the 37 vertices in each half of the polyhedron. Embodied in the fourth regular polygon is the power to generate the inner form of the Tree of Life in terms of its 1368 intrinsic yods, with the two topmost corners of its two hexagons coinciding with the lowest corners of the hexagons enfolded in the inner form of the next higher Tree, as well as its polyhedral form in terms of the 1368 sides of triangles that surround its axis 

We shall now proceed to analyse systematically the populations of geometrical elements and yods that surround an axis of the 144 Polyhedron drawn through any pair of its diametrically opposite vertices. We shall consider, firstly, the case when its faces and inner triangles are simple triangles or tetractyses and, secondly, the case when both are Type A triangles. The polyhedron with 216 edges and 144 faces has 72 vertices surrounding its axis, where 72 is the number of Chesed and 216 is the number of Geburah, the Sephirah following it. As the numbers 72, 144 & 216 has a highest common factor of 72, it is convenient to assign an integer, expressed in units of 72, to each corner, side and triangle as a weight indicating how many times that element occurs in the polyhedron:

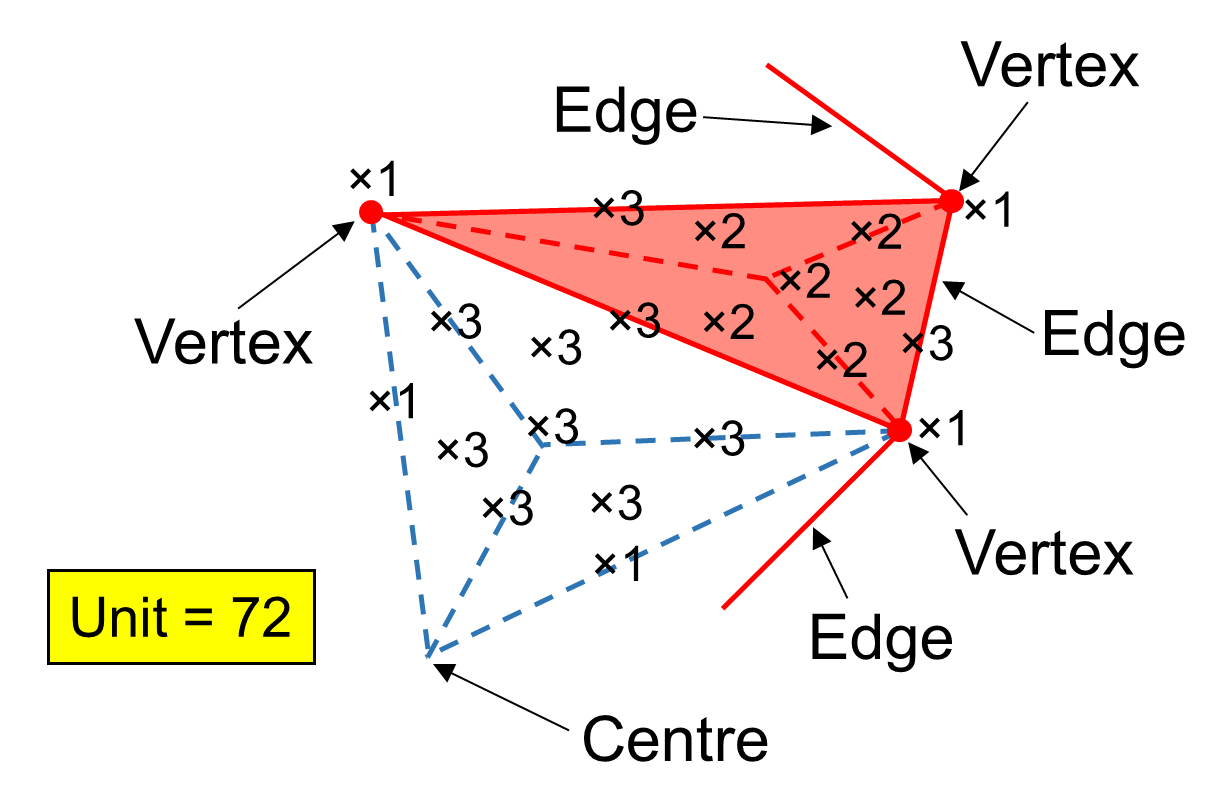
 The table below lists in terms of these weights the numbers of geometrical and yods that surround the axis of the 144 Polyhedron for the two cases.

Populations of geometrical elements and yods surrounding the axis of the 144 Polyhedron (1 unit = 72).

(C = no. of corners; S = no. of sides, T = no. of triangles, H = no. of hexagonal yods on sides, H′ = no. of central hexagonal yods).

Comments

• With simple triangles, the number of geometrical elements surrounding the axis is 10 units, i.e., 720. This is the number of yods surrounding the centre of a decagon with 2nd-order tetractyses as its sectors:

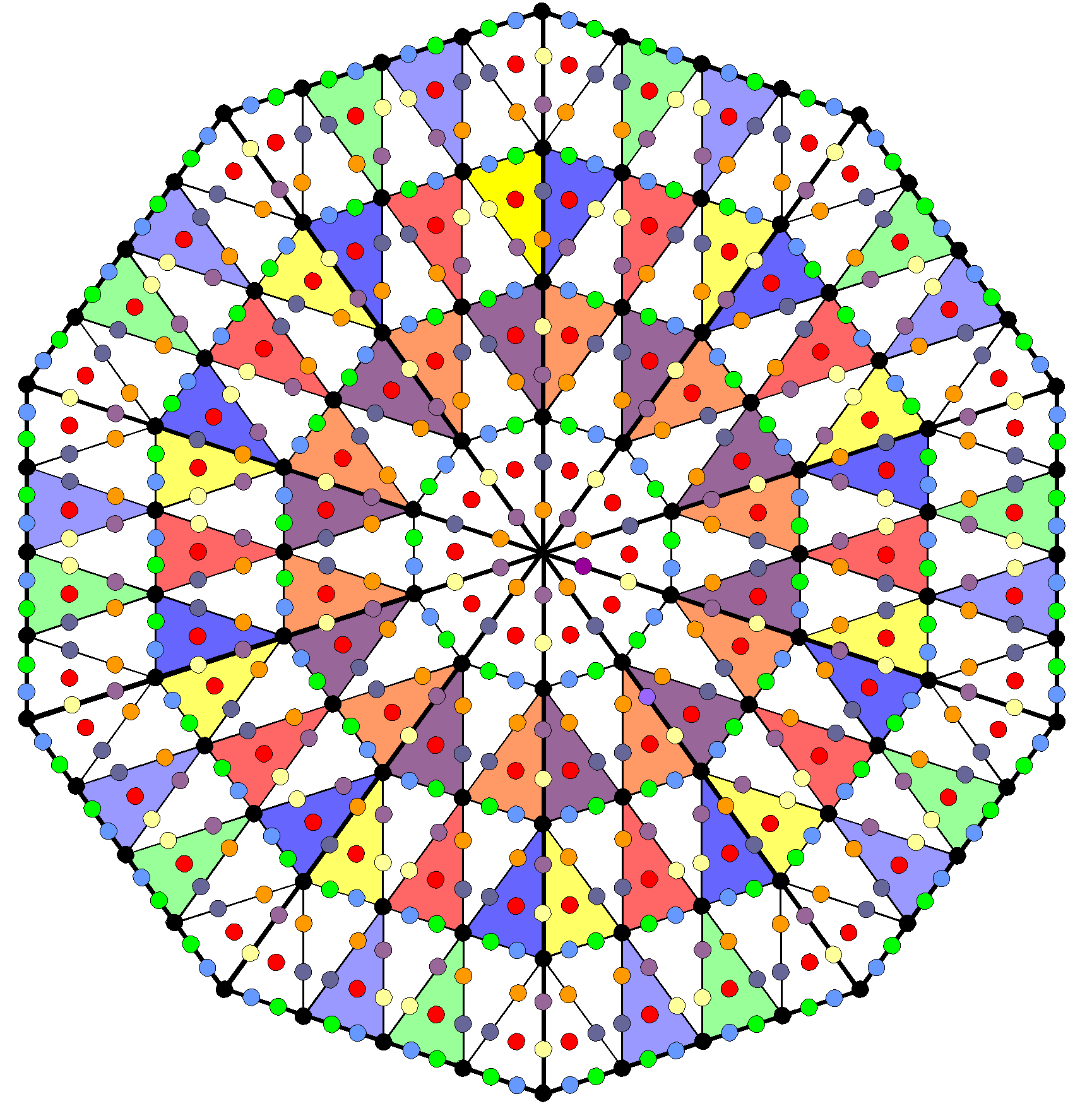
It demonstrates the Pythagorean perfection of the geometrical composition of the 144 Polyhedron.

• With simple triangles, there are (5×72=360) corners & sides surrounding the axis. As the latter comprises two vertices, two internal sides and the centre of the polyhedron, it consists of 365 geometrical elements. According to Greek gematria, this is the number of Abraxas, the highest Gnostic deity. The Gnostics, a sect of the second century CE believed that his name contained great mysteries, as it was composed of the seven Greek letters that formed the number 365, which is also the number of days in a year. Every day of the solar year can therefore be associated with one of the points or lines that make up the 144 Polyhedron.
• The number of yods lining edges = C + H = 7 units, i.e., 7×72 = 504. This is a parameter of CTOL, being the number of SLs down to (and including) the top of the 7-tree that maps the physical plane, i.e., the manifestation of space-time. It is also the number of yods outside the root edge in the inner Tree of Life that are unshared with its outer form. There are 504 of yods surrounding the centre of a heptagon with 2nd-order tetractyses as its sectors and 504 yods surrounding the centre of a Type C dodecagon: 

When they are Type C, the pair of dodecagons making up the inner Tree of Life have as many yods (2×504) as the 144 Polyhedron, namely, 14 units, or 14×72 = 2×504 yods. Each dodecagon corresponds to a half of the polyhedron.

• When its faces and internal triangles are Type A, it has (19×72=1368) sides surrounding its axis. Including the two sides making up its axis, it has 1370 sides. Remarkably, this is the number of yods in the inner Tree of Life with Type B polygons (see above). Surrounding the axis are (6×72=432) corners and (19×72=1368) sides, i.e., 1800 corners & sides. This number factorises as 50×36,  where 50 is the number value of ELOHIM, the Godname assigned to Binah, and 36 is the number of ELOAH, the Godname assigned to Geburah, which is the Sephirah below Binah in the Tree of Life.
  

• The number of yods lining sides of simple triangles = C + H = 3 + 18 = 21 units, or 21×72 = 1512. This is generated by assigning the number 21 of EHYEH, the Godname of Kether, to each of the 72 yods surrounding a Type A dodecagon: 

1944 =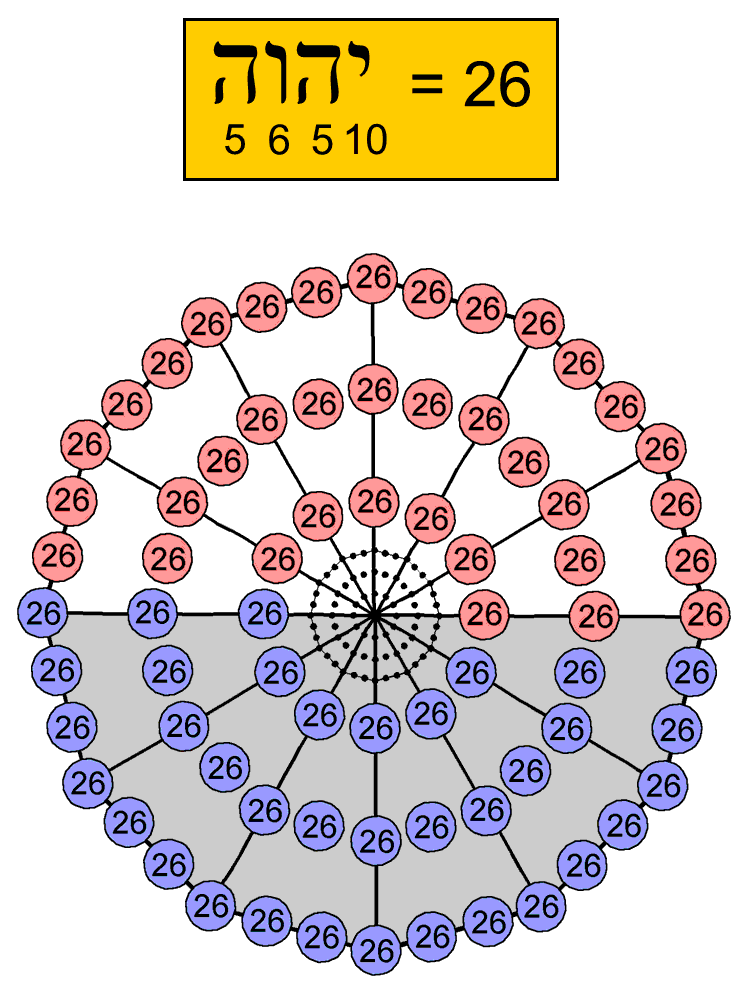

• The number of yods in the Type A faces that surround the axis = 27 units, or 27×72 = 1944. Of these, one unit, i.e., 72, are vertices, leaving 26 units, or 72×26 yods. Assigning the number value 26 of YAHWEH (יהוה) to the 72 yods surrounding the centre of a Type dodecagon generates the number of yods needed to be added to the faces shaping the 144 Polyhedron, given the 72 vertices surrounding its axis, which can be symbolised by the 72 yods in another dodecagon at its centre (see diagram above). The white and gray mathematical halves of the dodecagon correspond to the two halves of the polyhedron. The total number of yods =  59 units, of which 15 units are hexagonal yods at centres of tetractyses. The number of yods lining simple triangles = 59 − 15 = 44 units, or 3168. Including the three yods on the central axis on either side of the centre, there are 3174 boundary yods surrounding the latter, that is, 3100 yods other than vertices. Each half of the polyhedron is lined by 1550 yods other than vertices. This is the number of yods in 155 tetractyses. It shows how ADONAI MELEKH, the Divine Name assigned to Malkuth with number value 155, prescribes the form of the 144 Polyhedron in terms of the yods lining all its tetractyses. As 59×72 = 2×59×36 and a Type A dodecagon has 60 hexagonal yods, 59 hexagonal yods are associated with each dodecagon. Weighted with the number 36 of ELOHA, the Godname of Geburah, the 118 hexagonal yods in the two joined dodecagons generate the number yod population of the 144 Polyhedron:

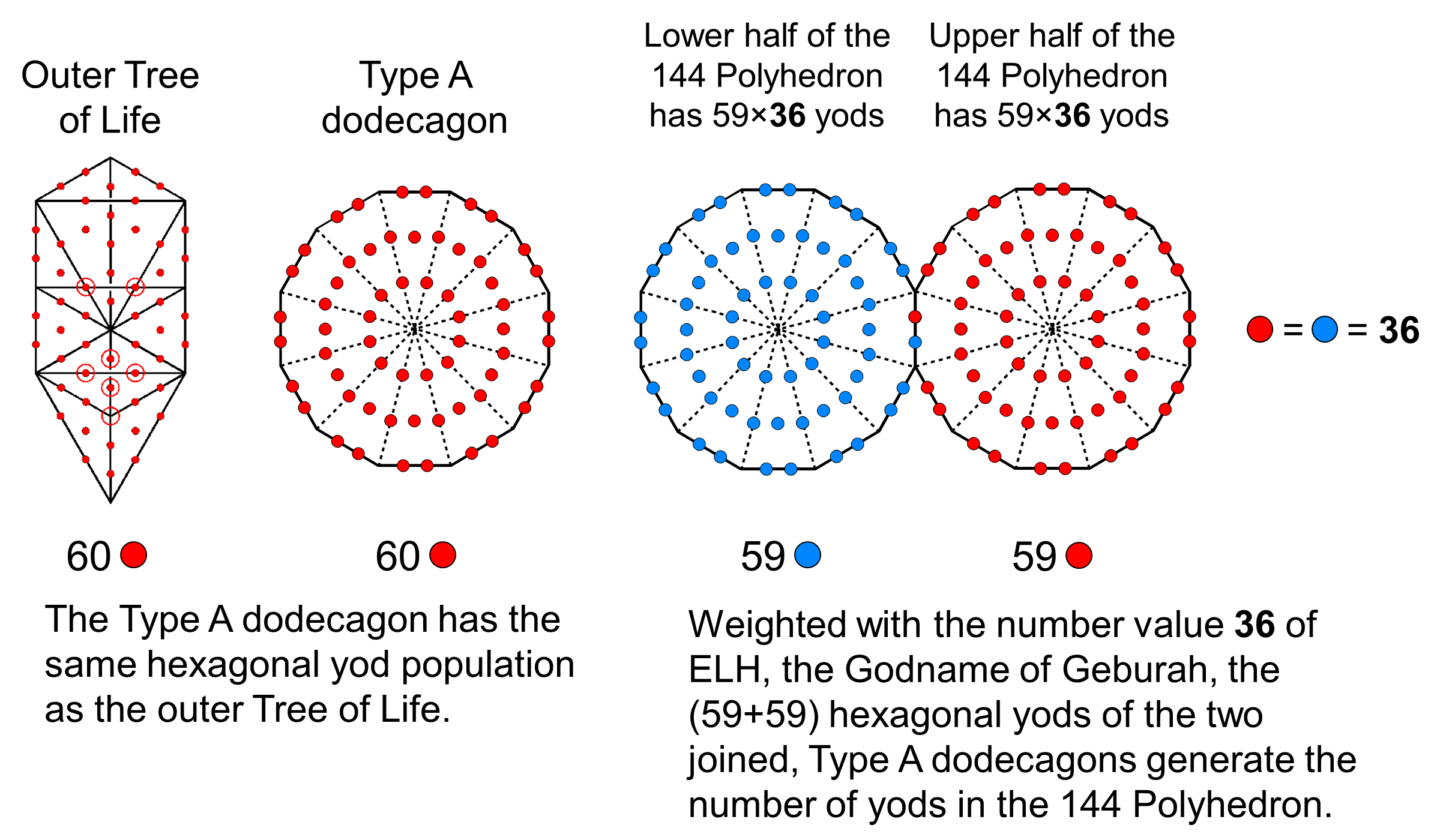
The two hexagonal yods in the root edge denote the 72 vertices surrounding its axis, 36 being in each half. As additional evidence of the pair of joined dodecagons generating the yod population of the 144 Polyhedron, the diagram below shows that the 59 hexagonal yods associated with each one form complete subsets whose numbers are various combinations of the weights given in the table above:

• The axis of the disdyakis triacontahedron is surrounded by 60 vertices, 180 edges & 120 triangular faces. Notice that, in units of 60, they are in the same 1:3:2 proportion as the 72 vertices, 216 edges & 144 faces are when a unit of 72 is used for the 144 Polyhedron. This is very significant. The two polyhedra are, of course, entirely different in shape, but they exhibit the same relative proportions of the three classes of geometrical elements that make up their faces, albeit with number bases of 72 and 60, which are in the ratio of 6:5. This means that the numbers of corners, sides, triangles and yods in the disdyakis triacontahedron are exactly 5/6 the corresponding numbers in the 144 Polyhedron and that the total population of any type = (1+5/6=11/6) that of the 144 Polyhedron (or 11/5 that of the disdyakis triacontahedron). All geometrical or yod populations of the 144 Polyhedron are 6/11 of the pair of polyhedra and all populations of the disdyakis triacontahedron are 5/11 of the total. The numbers displayed in the table shown above for the 144 Polyhedron apply to the disdyakis triacontahedron (indeed, to any other polyhedron whose numbers of vertices surrounding its axis, edges & faces are in the proportions 1:3:2). The only difference is that the unit is 60, not 72. For a polyhedron with V vertices, E edges and F faces, the numbers E and F are related by Euler's famous polyhedron formula:

•  V − E + F = 2,

  where V = 2 + C and C is the number of vertices surrounding its axis. If E = pC and F = qC, where p and q are not necessarily integers, we find:

  p = q + 1.

Therefore, if q = 2, then p = 3. The specialness of the 144 Polyhedron is that both it and its parent polyhedron have twice the number of faces as the number of its vertices surrounding an axis, although this property is not unique amongst polyhedra with triangular faces. For example, the tetrahedron, octahedron and icosahedron are the three Platonic solids with triangular faces and they conform to the same 1:3:2 proportions because they have the respective proportions 2:6:4, 4:12:8 and 10:30:20. The table shown above applies to them as well, with respective unit sizes of 2, 4 and 10. The reason why the 144 Polyhedron displays the proportion 1:3:2 is that it starts with the disdyakis dodecahedron, which has 24 vertices surrounding its axis, 72 edges & 48 faces, i.e., it displays the same proportion, and then the attachment of tetrahedra to its faces happens to leave this proportion unchanged:

(non-bold numbers are numbers of each added type of geometrical element in a tetrahedron)

• According to the table, the number of yods lining edges of the 144 Polyhedron and surrounding its axis when its faces are tetractyses = C + H = 1 + 6 = 7 units, i.e., 7×72 = 504. When its faces are Type A triangles, this number = 3 + 18 = 21 units (seven additional units, or 504 yods, in each half). The 1512 boundary yods comprise three sets of 504 yods: 1512 = 3×7×72. Alternatively, this triple division arises from the fact that the 72 vertices consist of the 48 peaks of the 48 tetrahedra stuck to the 48 faces of the disdyakis dodecahedron (24 in each half), which has 24 vertices surrounding its axis, in which case, 1512 = 21×3×24. Inserting the factorisation: 21 = 3×7 created (as we have just seen) by the distinction between simple triangles and Type A triangles, the 144 Polyhedron exhibits the factorisation: 1512 = 3×7×3×24. This number and this factorisation appears carved into stone on a world-famous archeological site whose identity will be revealed in the author's forthcoming book.

• For the disdyakis triacontahedron, the unit for calculating populations of geometrical elements and yods is 60, so that the number of yods lining sides of the (6×60=360) triangles in its 120 faces = 21×60 = 1260. This is the number value of the class of angels called "Tarshishim" that is assigned to Netzach. Comparing the two polyhedra, the (144×3=432) triangles in the 144 faces of the 144 Polyhedron are shaped by 1512 yods, that is, by 1440 (=144×10) yods other than vertices, whilst the (120×3=360) triangles in the 120 faces of the disdyakis triacontahedron are shaped by 1260 yods, that is, by 1200 (=120×10) yods other than vertices. Both polyhedra have (144+120=264) faces that require (1440+1200=2640=264×10) additional yods to create them from tetractyses. Here is remarkable evidence confirming that the two polyhedra consitute the Polyhedral form of the inner Tree of Life, its seven enfolded polygons having 264 yods (120 lining their 42 sides, inside which are 144 yods). It is as though the Polyhedral Tree of Life were expressing the inner form of 10 separate Trees of Life, each representing a Sephirah, the 144 Polyhedron corresponding to the interiors of the seven enfolded polygons and the disdyakis triacontahedron corresponding to their boundary and expressing the form of the inner form of the ten Trees of Life.

• The weight for calculating the number of corners, sides & triangles surrounding the axis of a polyhedron with (2+N) vertices, 3N edges & 2N faces is 40. For the 144 Polyhedron and disdyakis triacontahedron, which have these properties with, respectively, N = 72 and N = 60, these numbers are (40×72=2880=288×10) and (40×60=2400=240×10). The total number of geometrical elements surrounding their axes = 2880 + 2400 = 5280 = 528×10. Each half of the Polyhedral Tree of Life has 264×10 geometrical elements made up of the 144×10 elements in the 144 Polyhedron and 120×10 elements in the disdyakis triacontahedron. This is the polyhedral counterpart of the 144 yods inside the boundaries of the seven enfolded polygons in each half of the inner Tree of Life and the 120 yods lining their sides, that is, the 528 yods in the set of seven enfolded polygons and their mirror image, considered separate from each other. The inner form of 10 separate (i.e., not overlapping) Trees of Life consists of 10 sets of seven enfolded polygons with a total of 2640 yods and their mirror images with 2640 yods. They consist of 1200 boundary yods and 1440 internal yods that correspond to the 1200 geometrical elements in each half of the 120 Polyhedron and the 1440 elements in each half of the 144 Polyhedron. The factor of 10 indicates that the Polyhedral Tree of Life is the polyhedral version of the inner form of 10 separate Trees of Life, each Tree representing one of the 10 Sephiroth of a single Tree of Life. The distinction between the Supernal Triad and the seven Sephiroth of Construction expresses itself as three Trees of Life whose inner form has (3×528=1584) yods and seven Trees whose inner form has (7×528=3696) yods. Any sacred-geometrical representation of the triple Godhead must consist of 1584 irreducible components arranged as three sets of 528 components. There are two mysterious stone formations known to the author in different parts of the world that have this precise pattern and whose meaning he has deciphered. One of them can be found on his website here. As 1584 = 22×72 = 24×66 = 12×132 and the weight for the corners & sides in the faces of a polyhedron described by the table of weights is (3+9=12), the number 1584 is the number of points & lines in the 264 faces of the two polyhedra constituting the Polyhedral Tree of Life. As the sum of the (12×72=864) points & lines in the 144 faces of the 144 Polyhedron and the (12×60=720) points & lines in the 120 faces of the disdyakis triacontahedron, it is a structural parameter of any representation of the Divine Whole or a holistic system that embodies this paradigm. The two numbers 864 & 720 have the same 6:5 ratio as the numbers of vertices that surround the axes of the 144 Polyhedron and disdyakis triacontahedron and as the numbers of boundary and internal yods of the seven enfolded polygons making up the inner Tree of Life: 120/144 = 5/6. It manifests in the trunk and branches of the outer Tree as the 10 sides of the five triangles in the former and the 12 sides of the 11 triangles in the latter. It indicates that the disdyakis triacontahedron should be regarded as the trunk of the polyhedral Tree of Life and the 144 Polyhedron should be seen as its branches. The following correspondences exist:

trunk of Tree of Life → boundary of 7 enfolded polygons → disdyakis triacontahedron

branches of Tree of Life → interior of 7 enfolded polygons → 144 Polyhedron.

The outside of the Polyhedral Tree of Life makes up 5/11 of the whole and its inside makes up 6/11, e.g., for the 22 Paths of the outer Tree of Life, ((5/11)×22=10) Paths belong to its trunk and ((6/11)×22=12) Paths belong to its branches, whilst for the seven enfolded polygons in the inner Tree of Life, ((5/11)×264=120) yods make up its boundary and ((6/11)×264=144) yods make up its interior. The weight 12 that determines the number of points & lines in the faces of the 144 Polyhedron is the sum of the weights 1 (vertices), 2 (corners), 3 (edges) & 6 (sides). Hence, it is the sum of the weights (1+3=4) (vertices & edges), 2 (corners) and 6 (sides). This 4:2:6 division of the weight 12 into points and lines of different types, as well as the multiplying number 72 (which becomes a unit of distance measured in feet) manifests in the shape and size of the stone formation referred to above.

• The total number of yods surrounding the axes of the two polyhedra = 59×(72+60) = 59×132 = 7788. Including the 12 yods on their axes other than their centres, the total yod population = 7800 = 65×120, where 65 is the number value of ADONAI, the Godname of Malkuth and the sum of the first ten integers after 1:

65 = 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11,

and 120 is the sum of the first ten odd integers after 1:

120 = 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21.

Here is undeniable evidence of the mathematical beauty shown by the construction of the Polyhedral Tree of Life when its building block is the ten-fold tetractys. The Godname ADONAI prescribes the number of yods needed to construct all the tetractyses that build the forms of its two polyhedra. As 120 yods line the seven enfolded polygons of the inner Tree of Life, they generate, when weighted with the number 65 of ADONAI, the number of yods in its polyhedral counterpart that surround the centres of the 144 Polyhedron and the disdyakis triacontahedron. The integers 6 and 5 present in 65 also express the ratio of the yod populations of the 144 Polyhedron and the disdyakis triacontahedron because they equal 59N, where N = 72 for the former and 60 for the latter, i.e., their ratio is 6/5.

• Weighted with the number 33, the 236 yods lining the (7+7) enfolded polygons of the complete inner Tree of Life represent the number of yods surrounding the axes of the two polyhedra because 59×132 = 59×4×33 = 236×33. The number 33 is the average number of vertices per polyhedral half (33 = (36+30)/2), where 36 is the number of vertices in each half of the 144 Polyhedron and 30 is the number of vertices in each half of the disdyakis triacontahedron). 

As shown above, the four yods in the root edge separating the two sets of polygons generate the 132 vertices surrounding the axes, the 104 yods lining the pair of octagons and the pair of dodecagons generate the number of other yods in the 264 faces of the two polyhedra, and the 128 yods lining the sides of the ten other polygons generate the number of internal yods. It is readily verified that no other combinations of polygons have 64 or 52 yods lining their sides outside the root edge. The number 33 is the number of corners of the seven enfolded polygons that do not coincide with corners of triangles belonging to the outer Tree of Life. It measures those corners that are intrinsic to its inner form. As the number of corners of the polygons making up the inner form of the n-tree = 68n + 2, where "2" denotes the topmost corners of the two hexagons, which are shared with the inner form of the next higher Tree of Life, there are 68 corners per set of 14 polygons, i.e., 66 corners outside the root edge, so that 33 such corners are intrinsic to each set of seven enfolded polygons. One endpoint of the root edge can be asociated with one set of polygons with 33 intrinsic corners and the other endpoint can be asociated with the other set with 33 intrinsic corners. The counterpart of this "1+33" association in the Polyhedral Tree of Life is one of the two "poles" that an axis has and the 33 vertices that surround it on average in each half of the two polyhedra.

• The number weights whose ratios are the tone ratios of notes in the Pythagorean musical scale form an infinite, two-dimensional hexagonal lattice. Any number weight is of the form N = 2^p3^q, where p = 0, ±1, ±2, etc and q = 0, ±1, ±2, etc. The number n = 2^r3^s is located at the intersection of the row of weights with p = r and the row with q = s. It is the centre of a tetractys of 10 number weights, all of which are n/6 times their counterpart in the Lambda Tetractys. In other words, the latter gets shifted and multiplied by the same factor of n/6. Every number weight is the product of 2 and 3 raised to the powers of positive or negative integers. The ratio of any two number weights n and m = 2^t3^u is n/m = 2^(r−t)3^(s−u), which is the number weight located at the intersection of the (r−t) row and the (s−u) row. This means that any number weight is also the tone ratio of a musical note. They are, of course, still ratios, not actual frequencies, as the latter are set by whatever magnitude the freqency of the fundamental is. This is analogous to how the table given above lists the number weights for any polyhedron with (2+N) vertices, 3N edges and 2N triangular faces, not just for the 144 Polyhedron, for which N = 72, or for the disdyakis triacontahedron, for which N = 60. The number N corresponds to the fundamental frequency, which is arbitrary. But these two values of N are not arbitrary — they characterise the Polyhedral Tree of Life. We have already seen how, as numbers of vertices, these two numbers are unique in that the numbers of edges that they imply — 144 & 120 —parameterise the interior and boundary of the polygonal form of the inner Tree of Life. To understand their unique significance more, let us explore the musical analogy. Just as any note of the Pythagorean scale has a tone ratio that is the product of an integer power of 2 and an integer power of 3, so the proportions of any polyhedron that is a candidate for either polyhedron in the Polyhedral Tree of Life must have the proportion 1:3:2 for the relative numbers of their vertices, edges & faces. The numbers of the Lambda Tetractys are the numbers of different sets of weights for the vertices, edges & faces of this polyhedron, as well as various combinations of these geometrical elements:

1 → C = 1;
2 → T = 2;
3 → S = 3;
4 → C + S = 4;
6 → C + S + T = 6 (= T for Type A triangles);
9 → C + H + H′ = 9;
8 → H + H’ = 8;
12 → C + S = 12 (Type A faces);
18 → C + S + T = 18 (Type A faces);
27 → C + H + H′ = 27 (Type A faces).

Notice that "9" and "27" in the Lambda Tetractys are the total weights for the polyhedron whose faces are, respectively, simple triangles and Type A triangles. The central integer "6" corresponds to the weight 6 for number of triangles in the case where all faces are Type A triangles. Shown below is the tetractys of number weights centred on the number weight N:

The sum of the weights at its corners = 6N; If N is the number of vertices surrounding the axis, 6N is the number of tetractyses in the 2N Type A faces, the sum of the remaining seven weights is 9N, which is the number of tetractyses in the interior of the polyhedron, so that the sum of all 10 weights = 15N, which is the number of tetractyses in the polyhedron. Notice that the number value of YAH, the older Godname assigned to Chokmah, prescribes the number of tetractyses in the faces and interior of the polyhedron (it also determines the number of sides & triangles in its Type A faces).

• As 72 = 8×9 = 2³×3² and 108 = 2²×3³, these numbers are the only number weights whose powers of 2 and 3 are 2 and 3. The number 72 is the number of Chesed and is of unique significance to Kabbalah, being the number of "Names of God." Hindus regard 108 as a sacred number, referring in yoga to spiritual completion. Malas used for japa (silent repetition of a mantra) are composed of 108 beads and pranayama is completed in cycles of 108. It is the 21st harmonic in the Pythagorean scale. The two numbers are both arithmetic means of sets of four things:

72 = ¼(1¹ + 2² + 3³ + 4⁴)

(1, 2, 3 & 4 are the numbers of yods in the four rows of the tetractys)

108 = ¼(3³ + 4³ + 5³ + 6³)

(3, 4, 5 & 6 are the number of corners of the first four types of polygons: triangle, square, pentagon & hexagon). The number 72 is also the arithmetic mean of the cubes of 3, 4 & 5:

72 = ⅓(3³ + 4³ + 5³).

The table indicates that the weight for corners of tetractyses in the 144 Polyhedron with Type A triangles is 6, i.e., the total number of corners of tetractyses surrounding its axis = 6×72 = 432, where

432 = 3³ + 4³ + 5³ + 6³.

This is the number of hexagonal yods at the centres of the faces. It is the sum of the number weights at the corners of the tetractys with 72 at its centre:

12 + 96 + 324 = 432.

whilst the sum of the seven other number weights is 648 (=9×72), which is the number of hexagonal yods at centres of tetractyses inside the 144 Polyhedron, the weight for this being 9, according to the entry for H′ in the table shown above. The weight for corners other than vertices is 5, leaving a weight of 54 for all vertices and hexagonal yods, i.e., (54×72=108×36=3888) yods. The weight for all hexagonal yods in the 144 faces is 24, i.e., the number of such hexagonal yods = 24×72 = 8(3³+4³+5³) = 2³(3³+4³+5³) = 6³ + 8³ + 10³ = 12³. This number is determined by the Decad (10) because the tenth type of polygon (the dodecagon) has 12 corners and assigning 12² to each corner generates 12³.

• For a polyhedron with N vertices surrounding its axis, 3N edges and 2N triangular faces, there are 6N triangles in its faces when they are Type A and 9N internal triangles — a total of 15N triangles:

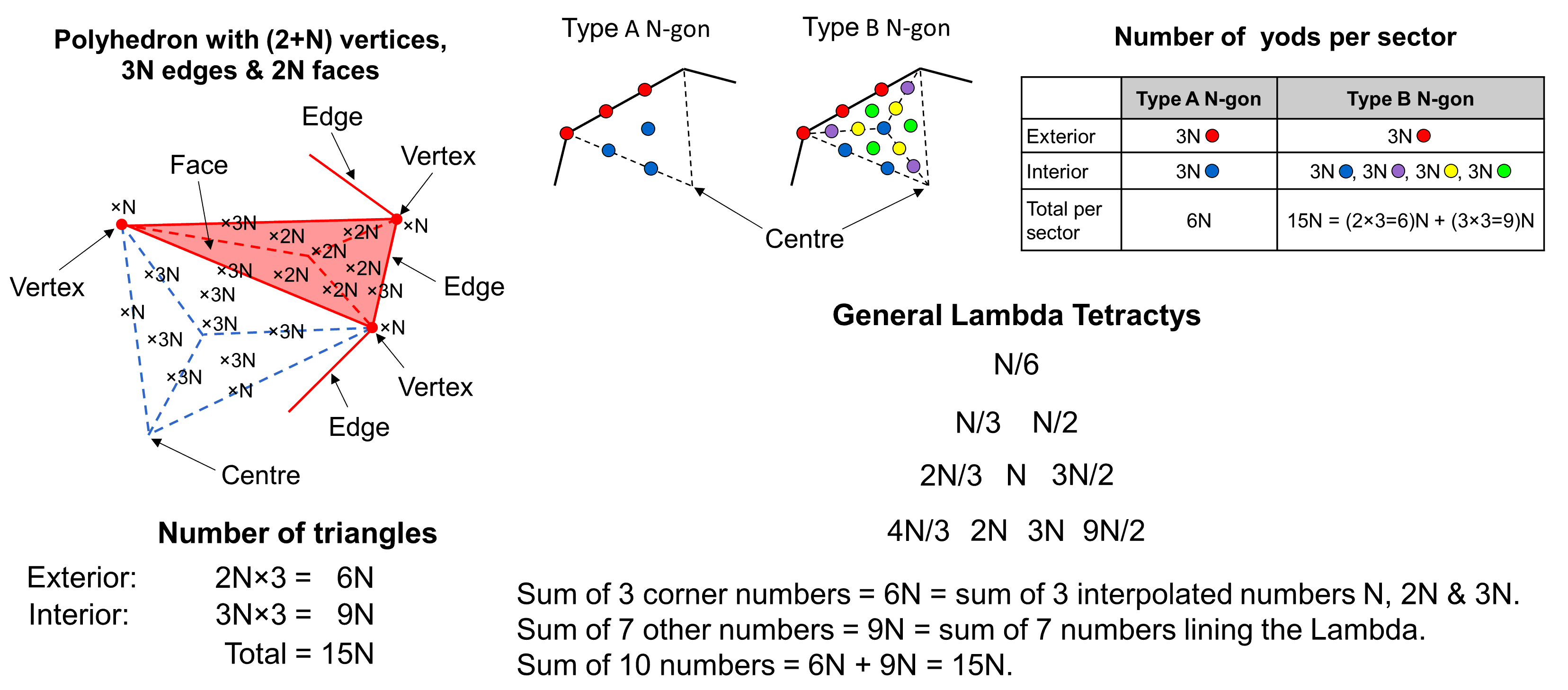
This 6:9 division appears in the Type B N-gon. For the Type A n-gon, there are six yods per sector (three on its external side, three inside it). Hence, 3N yods line the sides of the N-gon, inside which are 3N yods. The two sets of 3N yods compare with the 3N triangles in the N faces of each half of the polyhedron. For the Type B n-gon, nine yods are added to each sector. They comprise a set of three hexagonal yods (coloured green in the diagram above) at centres of tetractyses and three pairs of hexagonal yods lining their sides, or, alternatively, two sets of three hexagonal yods of the same colour (yellow & violet).  The nine extra yods therefore consist of three sets of three, so that the 9N additional yods comprise three sets of 3N yods; this compares with the 9N triangles inside the polyhedron, which consist of three sets of 3N triangles. If we count just its basic triangles, the (N+2)-vertex polyhedron is analogous to the Type B N-gon or any set of Type B polygons with N corners. The counterpart in the inner form of the Tree of Life of the 144 Polyhedron with (2+72) vertices is the first (6+6) separate polygons, which have (36+36=72) corners and (72×15=1080) yods surrounding their centres, comparing with the 1080 triangles in the 144 Polyhedron. Each set of six polygons with 36 corners corresponds to each half of the polyhedron with 36 vertices surrounding its axis. The number 15 is the number value of YAH (יה), the older Godname assigned to Chokmah. The value 5 of the letter heh (ה) denotes the weight of 5 for triangles in the 144 Polyhedron when its faces are simple triangles, whilst the value 10 of the letter yod (י) denotes the increase of weight by 10 when all these triangles become Type A triangles.

The "beauty" of the 144 Polyhedron
The Type A 72-gon has (6×72=432) yods surrounding its centre, where

432 = 3³ + 4³ + 5³ + 6³.

This is the number of triangles in the 144 Type A faces of the 144 Polyhedron, as well as the number of corners of its (15×72=1080) triangles. It is also the number of yods surrounding the centre of a hexagon with 2nd-order tetractyses as its sectors, for each one has 85 yods, 72 yods per sector, and 6×72 = 432. The Type B 72-gon has (72×15 + 1 = 1081) yods. This is the number of yods in a 15-gon whose sectors are 2nd-order tetractyses because 15×72 + 1 = 1081. The number 1081 is the gematria number value of Tiphareth (תפארת), meaning "beauty." This is the sixth Sephirah and the fifth Sephirah of Construction, counting from Malkuth. Its title signifies not merely the beauty of outer form but the perfect balance between this form and the function it serves. Only a polyhedron with 72 vertices surrounding its axis and 216 edges, namely, the 144 Polyhedron, has a polygonal counterpart that embodies the number 1081 of Tiphareth. Because of this property, it is unique.

As one of an infinite hexagonal lattice of musical weights, the number weight N is the centre of a general "Lambda Tetractys" of 10 number weights that are N/6 times their counterparts in the historically known Lambda Tetractys. As the sum of the latter is 90, the sum of the numbers in its general version is 15N. A Type B N-gon is its polygonal counterpart because 15N yods surround its centre. The sum of the weights at its three corners is 6N; this is also the sum of the three numbers added by interpolation of the seven numbers making up the general Lambda. The sum of the seven other numbers is 9N; this is also the sum of the seven numbers that form the general Lambda. The corresponding 6:9 divisions in the three, mathematically analogous systems are:

This 9/6 ratio is 3/2. Its musical counterpart is the tone ratio 3/2 of the perfect fifth, the fundamental division of the octave, being the arithmetic mean of the tone ratios of the first (1) and last notes (2) of any octave. The number of faces in the polyhedron is twice the number of its vertices and the number of edges in each half is 3/2 time the latter. The vertices play the role of the starting note in a musical scale and the centres of the faces are the counterpart of the octave, the edges in each half acting as the midway between them. The geometry of the 144 Polyhedron represents the spatialisation of the octave of sound.

 

<< Previous    1...   5  6  7  [8]  9    Next >>

Home