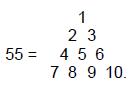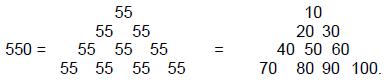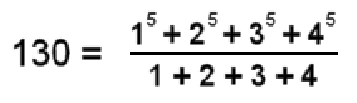ARTICLE 49
"As above, so below."
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
|
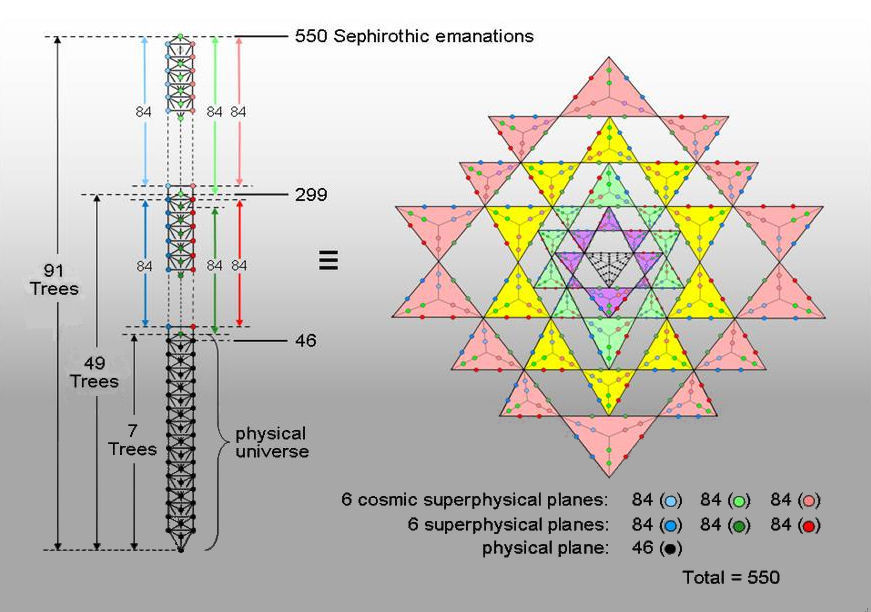
The triangular array of ten points, or tetractys, at the heart of Pythagoras' philosophy can be regarded as but the first member of an infinite sequence of higher order tetractyses. The mathematical realisation of the Hermetic axiom "as above, so below" is the Cosmic Tetractys in which the centre of a 2nd-order tetractys is another 2nd-order tetractys. Its 91 1st-order tetractyses represent the 91 subplanes of the seven cosmic planes of consciousness expounded by Theosophy. As the ten points of the tetractys denote the ten Sephiroth of the Tree of Life, the Cosmic Tetractys is equivalent to 91 overlapping Trees of Life (CTOL) with 550 Sephirothic emanations. As well as its outer form known to Kabbalists, the Tree of Life has an inner form consisting of two enfolded, similar sets of seven regular polygons that share one 'root edge.' Constructed from tetractyses, a unique set of twelve of these separate polygons, together with this root edge, have 91 corners and 550 yods. The Inner Tree of Life encodes the replication of its outer form to encompass all levels of reality. One set of seven polygons represents the cosmic physical plane and the five others represent the six cosmic superphysical planes. As independent evidence supporting this interpretation, the gematria number value of the Kabbalistic name of the Mundane Chakra of Malkuth (the physical level of the Tree of Life) determines the geometrical composition of the 49 Trees of Life that map the cosmic physical plane, whilst this map embodies the number value of Malkuth when constructed from tetractyses. The Sri Yantra is shown to be the counterpart of CTOL because the numbers 91 and 550 are embodied in its geometry. They are also embodied in the five Platonic solids because 550 points, lines & triangles are needed to construct their 50 faces, whilst the 90 interior triangles formed by their vertices and shared centre have 270 sectors with 91 corners. Constructed from tetractyses, the faces of the dodecahedron contain 550 points other than corners of tetractyses. The faces of the first four Platonic solids, which the ancient Greeks believed were the shapes of particles of the elements Earth, Water, Air & Fire, are constructed from the 248 corners & sides of 120 triangles, showing how they embody the dimension 248 of the superstring gauge symmetry group E8. Previous work established that the outer form of the polyhedral version of the Tree of Life is the disdyakis triacontahedron. Its 60 vertices surrounding an axis passing through two opposite vertices of a certain type are corners of 15 polygons. Including these two vertices, they possess 550 vertices, sides & triangles when their sectors are divided into three triangles. The eight polygons in one half of the polyhedron are composed of 299 geometrical elements. This is the number of Sephirothic emanations in the 49 Trees of Life mapping the cosmic physical plane. The 251 elements in the remainder of the polyhedron correspond to the 251 emanations in the 42 Trees of Life that map the six cosmic superphysical planes. The interior geometry of the disdyakis triacontahedron therefore represents CTOL. This is confirmed by the fact that the number of yods in the 15 polygons surrounding the centre of the polyhedron is the number of yods on the central pillar of CTOL between its apex and nadir when its triangles are tetractyses. |
1
Table 1. Gematria number values of the ten Sephiroth in the four Worlds.
ANGELS
CHAKRA1 Kether
(Crown)
620EHYEH
(I am)
21Metatron
(Angel of the
Presence)
314Chaioth ha Qadesh
(Holy Living
Creatures)
833
Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
6362 Chokmah
(Wisdom)
73YAHWEH, YAH
(The Lord)
26, 15Raziel
(Herald of the
Deity)
248Auphanim
(Wheels)
187Masloth
(The Sphere of
the Zodiac)
1403 Binah
(Understanding)
67ELOHIM
(God in multiplicity)
50
Tzaphkiel
(Contemplation
of God)
311
Aralim
(Thrones)
282
Shabathai
Rest.
(Saturn)
317Daath
(Knowledge)
4744 Chesed
(Mercy)
72EL
(God)
31Tzadkiel
(Benevolence
of God)
62Chasmalim
(Shining Ones)
428
Tzadekh
Righteousness.
(Jupiter)
1945 Geburah
(Severity)
216
ELOHA
(The Almighty)
36
Samael
(Severity of God)
131
Seraphim
(Fiery Serpents)
630
Madim
Vehement Strength.
(Mars)
956 Tiphareth
(Beauty)
1081
YAHWEH ELOHIM
(God the Creator)
76Michael
(Like unto God)
101
Malachim
(Kings)
140
Shemesh
The Solar Light.
(Sun)
6407 Netzach
(Victory)
148
YAHWEH SABAOTH
(Lord of Hosts)
129
Haniel
(Grace of God)
97Tarshishim or
Elohim
1260
Nogah
Glittering Splendour.
(Venus)
648 Hod
(Glory)
15
ELOHIM SABAOTH
(God of Hosts)
153
Raphael
(Divine
Physician)
311
Beni Elohim
(Sons of God)
112
Kokab
The Stellar Light.
(Mercury)
489 Yesod
(Foundation)
80
SHADDAI EL CHAI
(Almighty Living
God)
49, 363Gabriel
(Strong Man of
God)
246
Cherubim
(The Strong)
272
Levanah
The Lunar Flame.
(Moon)
8710 Malkuth
(Kingdom)
496
ADONAI MELEKH
(The Lord and
King)
65, 155Sandalphon
(Manifest
Messiah)
280Ashim
(Souls of Fire)
351
Cholem Yesodoth
The Breaker of the
Foundations.
The Elements.
(Earth)
168
(All numbers from this table that are referred to in the article are written in boldface).
2
1. The Cosmic Tetractys
At the heart of the ancient Pythagorean teachings was the triangular array of ten points known as the tetractys (Fig. 1).The modern academic view is that it represented what the Pythagoreans regarded as the perfect number 10 (Decad) as the fourth, so-called 'polygonal number,' the four rows of one, two, three & four dots symbolising, respectively, a mathematical point, the two points at the ends of a straight line, the corners of a triangle and the four vertices of a tetrahedron. However, it was far more than that, as the oath made by members of Pythagoras' mystery school testifies:
"I swear by the discoverer of the tetractys,
Which is the spring of all our wisdom,
The perennial fount and root of Nature."The seminal importance of the tetractys to Pythagoreans was due to this figure being not merely symbolic, as most mathematicians have wrongly believed, but the actual template of sacred geometry that transforms the latter into numbers of fundamental significance to the mathematical design of the universe and therefore having scientific meaning. The notion of design, with its implication of a Designer, is anathema, of course, to many scientists who hold to the materialistic paradigm that the universe sprung into
existence without the assistance of God. Hence, they would reject the claim of the Pythagoreans that the tetractys has a profound, metaphysical meaning that reveals the mysteries of the universe. The author's previous 48 research articles have demonstrated beyond doubt that this view is wrong. The tetractys is a representation of the Kabbalistic Tree of Life, each of its ten points, or yods (from the Hebrew name 'yod' of the tenth letter of the Hebrew alphabet, which is shaped somewhat like a dot) corresponding to one of the ten Sephiroth (Fig. 2). The yods either at the
corners of a hexagon or at its centre will be called 'hexagonal yods.' They symbolize the seven Sephiroth of Construction. The yods at the corners of the tetractys denote the Supernal Triad of Kether, Chokmah and Binah and the central hexagonal yod denotes Malkuth.
Suppose that we replace each point of a tetractys by a triangle. The motive behind this is to express the idea that each point of the tetractys ('1st-order tetractys') is a potential tetractys in itself and a member of a higher-order tetractys, or '2nd-order tetractys' (Fig. 3). Each triangle is then turned into a copy of the whole of which it was a constituent. All the triangles in the 1st-order triangles at the corners of the 2nd-order tetractys shown in Fig. 3 have been left white in order to conform to the white triangles in the original 1st-order tetractys. The seven coloured triangles in the 1st-order tetractys become (72=49) coloured triangles in the 2nd-order tetractys. There are 17 points along each side of the 2nd-order tetractys that are corners of 16 triangles. The number of corners of the triangles on its boundary is 48.
3
This is the number value of Kokab, the Mundane Chakra of Hod. The number 48 is always a basic measure of the global nature of a holistic system, as has been demonstrated in many previous articles and as will be illustrated in subsequent sections. A triangular array of 153 points (Fig. 4), 17 points along each side, comprises 300 sides of 100 triangles that form a 2nd-order tetractys. Each of its ten 1st-order tetractyses is made up of the 15 corners & 30 sides of ten triangles, that is, 55 geometrical elements, where
This demonstrates how the Decad determines the geometrical composition of a 1st-order tetractys whose yods are triangles. As 150 = 15×10, YAH, the Godname of Chokmah with number value 15 and ELOHIM SABAOTH, the Godname of Hod with number value 153, prescribe the geometrical array of points underlying the 2nd-order tetractys, the ten 1st-order tetractyses each having 15 corners. The ten separate 1st-order tetractyses have (10×55=550) geometrical elements that become 535 geometrical elements in the 2nd-order tetractys when their corners
coincide, 15 corners disappearing in the process. Including the 18 points in the six triangular gaps between 1st-order tetractyses, the triangular array consists of (18+535=553) geometrical elements. Starting with three points as the three corners of a triangle, 550 more elements (150 corners, 300 sides & 100 triangles) are needed to create the triangular array, where
This demonstrates how the Decad determines the geometrical composition of a 2nd-order tetractys as well as a 1st-order tetractys. The number 550 will manifest in various sacred geometries discussed later.
Let us next take this transformation a step further but with the difference that only the central 1st-order tetractys in the 2nd-order tetractys is replaced by the 2nd-order tetractys (Fig. 5). This generates what will be called the 'Cosmic Tetractys.' Its central 2nd-order tetractys, which denotes the Sephirah Malkuth, contains (7×7=49) coloured triangles symbolizing the seven Sephiroth of Construction. 49 is the
4
number value of EL ChAI, the Godname of Yesod. The six 1st-order tetractyses surrounding it refer to the six Sephiroth of Construction above Malkuth and contain (6×7=42) coloured triangles. The seven Sephiroth of Construction are expressed in the Cosmic Tetractys by (49+42=91) coloured triangles, where
91 = 12 + 22 + 32 + 42 + 52 + 62.
Because the square of any integer n is the sum of the first n odd integers, 91 is the sum of (1+2+3+4+5+6=21) odd integers. This is the number value of EHYEH, the Godname of Kether. Explicitly,
15 integers form the boundary of the triangular array, showing how YAH prescribes this number. YAH also prescribes it because a 15-sided polygon with its sectors turned into 1st-order tetractyses has 91 yods. The sum of the integers is 65, the remaining six integers inside the boundary adding to 26. 65 is the number value of ADONAI ("My Lord") and 26 is the number value of YAHWEH. Out of reverence for the holy nature of YHVH (TETRAGRAMMATON) and because most Jewish denominations teach that it is forbidden to utter the Name of God except by the High Priest
in the Temple, Jews substitute it in prayers with ADONAI. 91 is the number value of ADONAI TETRAGRAMMATON.
The fact that the centre of the Cosmic Tetractys is another 2nd-order tetractys like itself can be regarded as the geometrical realisation of the Hermetic principle 'As above, so below.' As a map of all levels of consciousness (as we shall shortly see), the Cosmic Tetractys is somewhat analogous to a hologram. This reproduces a three-dimensional image of a scene, each point in the hologram containing light from the whole of the original scene. In principle, the latter can be reproduced from any part of the hologram, however small, although in practice, the image becomes fuzzier because diffraction causes a loss of resolution. All information about the whole holographic image is contained in any part. The purist may object that this analogy between a hologram and the Cosmic Tetractys breaks down because only the central 2nd-order tetractys is identical to the parent one — its nine other 1st-order tetractyses remain such in the Cosmic Tetractys. The criticism is misplaced. Every triangle representing a Sephirah is potentially a 1st-order tetractys and therefore also a 2nd-order tetractys. It is this fundamental property that is analogous to a hologram, not the geometry of the Cosmic Tetractys per se.
2. The Cosmic Tree of Life
The 91 coloured triangles in the Cosmic Tetractys symbolize all possible differentiations of the seven
5
Sephiroth of Construction subject to the requirement of consistency with the Hermetic principle of correspondences that all their 49 differentiations should appear as well in the last one, Malkuth. As a triangle is a potential 1st-order tetractys, which is simply a Pythagorean representation of the Tree of Life, it is deduced that the seven Sephiroth of Construction require 91 Trees of Life represent their cosmic manifestation. The Tree of Life counterpart of the Cosmic Tetractys therefore consists of 91 Trees of Life that overlap one another (Fig. 7). This scheme will be called the 'Cosmic Tree of Life,' or CTOL. As the yod at the centre of a tetractys corresponds to Malkuth in the Tree of Life, the cosmic physical level of CTOL corresponding to Malkuth consists of the lowest 49 overlapping Trees of Life, each one denoted by one of the 49 coloured triangles (potential tetractyses) that form the central yod (Malkuth) of the Cosmic Tetractys. The cosmic superphysical region of CTOL is defined by the set of 42 Trees of Life above the lowest 49 Trees of Life. They correspond to the 42 larger, coloured triangles (potential tetractyses) in Fig. 6 symbolizing the six Sephiroth of Construction above Malkuth.
A THEOSOPHICAL INTERPRETATION
H.P. Blavatsky, one of the founders of the Theosophical Society, stated in her book The Secret Doctrine that Creation is divided into seven great planes of consciousness. Many of her ideas, which her book proved are found in the creation mythologies of ancient religions like Judaism and Hinduism, were developed by later Theosophical writers, such as Annie Besant and Charles W. Leadbeater. In particular, Alice Bailey gave a more precise and detailed formulation of the Theosophical classification of the planes. We shall follow her terminology, which is now commonly used in mainstream, Theosophical literature.
The seven cosmic planes of consciousness are:
1) Adi, or Divine, plane;
2) Anupadaka, or Monadic, plane;
3) Atmic plane;
4) Buddhic plane;
5) Mental plane;
6) Astral plane;
7) Physical plane.Each cosmic plane is divided into seven cosmic subplanes. The seven subplanes of the cosmic physical plane are called 'solar planes.' The word solar was used not to imply any connection with the Sun but to convey a loose analogy (that is, not to be regarded in any literal sense) between the difference between the Solar System and the rest of the universe and the distinction between the cosmic physical plane and the six cosmic superphysical planes of consciousness. The solar planes, too, have the names listed above, e.g., Theosophists speak of the 'solar physical plane,' the 'solar astral plane,' etc. Each solar plane is further divided into seven solar subplanes. The solar physical plane consists of seven solar physical subplanes; the solar astral plane consists of seven solar astral subplanes, etc. The seven solar planes of the cosmic physical plane have (7×7=49) solar subplanes and the six cosmic superphysical planes (astral–adi) have (6×7=42) subplanes. All seven cosmic planes have (49+42=91) subplanes.
The seven planes (cosmic or solar) denote primary modalities of consciousness that correspond in a one-to-one way to the seven Sephiroth of Construction:
Adi
Anupadaka
Atmic
Buddhic
Mental
Astral
Physical—
—
—
—
—
—
—Chesed
Geburah
Tiphareth
Netzach
Hod
Yesod
MalkuthOnly the four lowest Sephiroth of the Tree of Life: Malkuth, Yesod, Hod and Netzach, are at present components of normal consciousness. They correspond in the human personality to the four psychological functions of, respectively, sensing, feeling, thinking and intuiting, identified by the great psychoanalyst, C. J. Jung. Atmic, or mystical, consciousness corresponds formally to what Jung called the "transcendent function of the psyche." It is the expression of Tiphareth. A one-to-one association similarly exists between the seven subplanes of a cosmic or solar plane and the seven Sephiroth of Construction. It must be emphasized that Theosophical planes are not synonymous with the latter. The Kabbalistic notion of the Sephiroth is more fundamental than the Theosophical concept of planes. The latter are modalities of consciousness that express the particular quality of their corresponding Sephirah.
Comparison of the Theosophical scheme of planes of consciousness with the Cosmic Tetractys shown in Fig. 6 establishes the following set of correspondences:
6
Central 2nd-order tetractys
6 surrounding 1st-order tetractyses
triangle of central 2nd-order tetractys
triangle of 6 surrounding 1st-order tetractyses—
—
—
—
6 higher Sephiroth of Construction
solar subplane.
cosmic subplane.
— cosmic physical plane.
— 6 cosmic superphysical planes.Each of the 91 coloured triangles yods corresponding to a Sephirah of Construction in the Cosmic Tetractys denotes a subplane of either a cosmic or a solar plane. Each subplane is represented in CTOL by a Tree of Life. The lowest seven Trees of Life denote the cosmic physical plane. The lowest seven overlapping Trees of Life denote the solar physical plane, the next seven Trees of Life represent the solar astral plane, and the third, higher set of seven Trees of Life denotes the solar mental plane, and so on. Similarly, Trees 50–56 denote the cosmic astral plane; Trees 57–63 represent the cosmic mental plane, etc. The 91 Trees of Life in CTOL are a map of the 91 subplanes of the seven cosmic planes of consciousness.
Definitions & formulae
1) A 'Sephirothic level' (SL) is a Sephirah of any Tree of Life in CTOL. It is depicted in Fig. 7 by a black dot. Trees of Life and SLs are counted from the base of CTOL. As Daath is not a Sephirah, Daath of the highest (91st) Tree is not an SL. It is depicted in Fig. 7 as a dotted circle. Daath of every Tree except the 91st is Yesod of the next higher Tree and is therefore an SL of that Tree. For the sake of brevity, the phase 'Tree of Life' will be replaced in most contexts by its acronym TOL (plural: TOLs).
2) The 'n-tree' is the section of CTOL consisting of the n lowest, overlapping TOLs. Notice that this is not the same as n overlapping TOLs because in the former case, Daath of the nth TOL is Yesod of the (n+1)th TOL and is connected to other SLs by Paths of that TOL, whereas in the latter case, it is not an SL and is not joined by Paths to SLs, the nth TOL looking like a single Tree of Life. CTOL is
7
obviously not the 91-tree but 91 overlapping TOLs.
The structure of CTOL is described by the following formulae:
1. Kether of the nth TOL is number
S(n) = 6n + 5 (1≤n≤90; S(91) = 550)
2. Kether of the nth TOL is the (2n+3)th SL on the central Pillar of Equilibrium (1≤n≤90); Kether of the 91st TOL is the 184th SL on the central pillar.
3. The nth SL on the central pillar is number
C(n) = 3n – 4 (3≤n≤183; C(1) = 1, C(2) = 2, C(184) = 550).
5. Kether of the nth TOL is tree level number
L(n) = 3n + 4 (1≤n≤90; L(91) = 276)
6. Number of tree levels up to the nth SL on the central Pillar is
T(n) = (3n–2)/2 (n even)
= (3n–1)/2 (n odd)
7. The n-tree has (n+1) Upper and Lower Faces.
8. Number of Paths in the n-tree is
P(n) = 16n + 6 (n overlapping TOLs)
= 16n + 9 ( n-tree)The 91 overlapping TOLs in CTOL has 550 SLs. Compare this with the facts established earlier that the ten 1st-order tetractyses that form the 2nd-order tetractys have 550 geometrical elements when they are separate and that 550 geometrical elements are needed to construct its underling triangular array of 153 points, starting from the three corners of a triangle. According to formula 1, the 49-tree mapping the cosmic physical plane has S(49) = 299 SLs. Hence, there are 251 SLs above it. The 7-tree has 47 SLs, so that its apex is the 504th SL from the top of CTOL. The lowest TOL is the 1-tree with 11 SLs, so that its top is the 540th from the top of CTOL. The Decad determines the number 91 because a decagonal array of the integers 1, 2, 3 & 4 symbolised by the tetractys add up to 91:
As the 13th triangular number, 91 is the number of points in the triangular array underlying a 1st-order tetractys in which each triangle is a tetractys:
The odd integers in the sum of the first 13 integers:
91 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13
8
add up to 49 and the even integers sum to 42. This arithmetic division created by the even and odd integers mirrors the division of the seven cosmic planes into the 49 subplanes of the cosmic physical plane and the 42 subplanes of the six cosmic superphysical planes.
The Godname ELOHA with number value 36 prescribes CTOL because 91 is the sum of the 36 integers (15 even, 21 odd) in the array:
5 5 5
4 4 4 4 4
3 3 3 3 3 3 3
2 2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 1 1 1 1.ELOHIM, the Godname of Binah with number value 50, prescribes the 550 SLs in CTOL because 550 = 10×55, where
55 = 12 + 22 + 32 + 42 + 52,
i.e., 550 is the sum of (10×5=50) squares of the integers 1–5. Therefore,
550 = 10
10 + 30
10 + 30 + 50
10 + 30 + 50 + 70
10 + 30 + 50 + 70 + 90.The Godname YAH with number value 15 prescribes the number 550 as the sum of 15 numbers. We saw earlier how the Decad determines the number 550 as 10×55, where 55 is the sum of the first ten integers. 55 is also the tenth, so-called 'Fibonacci number.' Named after the 13th century Italian mathematician Leonardo of Pisa, also called Fibonacci, these are numbers appearing in the infinite sequence of integers:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ...
They have the property that each is the sum of the two previous numbers. They are known to be present in the philotaxis of many flowers and plants. The ratio of successive Fibonacci numbers converges towards the Golden Ratio φ = (1+√5)/2 = 1.6180339887... . This is the ratio of adjacent sides of the Golden Rectangle ABCD:
It has the remarkable property that, when a square ADEF is cut away from it with a side equal to the shorter side of the Golden Rectangle, the sides of the remaining rectangle BCEF has the same proportion as those of the original rectangle and therefore it is another Golden Rectangle.
3. Encoding of CTOL in the Inner Tree of Life
Polygonal representation of the n-tree
When the n sectors of an n-sided polygon (not necessarily regular) are each turned into tetractyses, six yods are added per sector, so that (6n+1) yods are generated, the number '1' referring to its centre. According to formula 1 given above, the number of SLs in the n-tree is
S(n) = 6n + 5.
There are four SLs beyond Chesed of the nth TOL up to its top. Therefore, the number of SLs up to Chesed of the nth TOL = S(n) – 4 = 6n + 1, where the number '1' denotes the lowest SL and six SLs are added for each overlapping TOL: S(n+1) – S(n) = 6. But (6n+1) is the number of yods in an n-sided polygon. Such a tetractys-constructed polygon is therefore a representation of n overlapping TOLs as far as its highest Chesed. The central yod corresponds to the lowest SL, the pair of hexagonal yods on each side of the polygon, being unshared by adjacent sectors, correspond to Chesed and Geburah of each TOL because these are unshared with adjacent TOLs. The yods at the corners of the polygon correspond to Yesod of each TOL and the hexagonal yods at the centres of the sectors correspond to each Malkuth, except for the lowest one, which is denoted by the centre of the polygon. Enclosing the n-sided polygon in
9
a square completes the polygonal representation of the n-tree because the four corners of the square correspond to Kether, Chokmah, Binah and Daath of the nth TOL. The following correspondences exist:
& on internal edges of tetractysesInner Tree of Life
The Tree of Life has an inner form as well as its outer form well-known to Kabbalists. It has been analyzed in great detail in many previous articles but will be described again briefly here.
The Inner Tree of Life (Fig. 9) consists of two identical sets of seven regular polygons that are enfolded in one another and share one side, one set being the mirror image of the other. The seven regular polygons are the triangle, square, pentagon, hexagon, octagon, decagon & dodecagon. Each set of separate polygons have 48 sectors with 55 corners, showing that the tenth Fibonacci number is present in the inner TOL, quantifying its geometry. Enfolded, both sets of polygons have 70 corners, the 96 sectors having 80 corners, where 80 is the number value of
Yesod. The former are the counterpart of the 70 yods in a Tree of Life when its 16 triangles are tetractyses (Fig. 10a). The latter are the counterpart of the 80 yods in the 1-tree when its 19 triangles become tetractyses (Fig. 10b). The ten yods added to TOL when it turns into the 1-tree correspond to the centres of the ten polygons that are not also corners of them when they are enfolded, for the outer corner of the triangle coincides with the centre of the hexagon and the outer corner of the pentagon coincides with the centre of the decagon.
Table 2. Yod populations of the polygons.
Polygon Σ n
Σ (6n+1)
14 Triangle 13 Square 12 Pentagon 11 Hexagon 10 Octagon 9 Decagon 8 Dodecagon Root edge 7 Dodecagon 6 Decagon 5 Octagon 4 Hexagon 3 Pentagon 2 Square 1 Triangle We have seen that the yod population of an n-sided polygon is the number of SLs up to Chesed of the nth TOL. When polygons are combined, their added yod populations will in general no longer correspond to the number of SLs up to Chesed of some TOL. What will be of interest to us here are the exceptions to this. In other words, what section of CTOL (if any) corresponds to the yod population of the seven separate polygons (or, indeed, all 14 polygons of the Inner TOL or some subset of them)? Table 2 displays the yod populations of the 14 polygons — both individual and as a running sum, adding upwards
10
from the bottom of the table. They are separated by the root edge, one set of seven polygons being arranged in the reverse sequence of the other set (the issue of other possible arrangements will be addressed later). Reading upwards from the base of the table, we find:
1. the first five polygons have 26 vertices or tetractyses and 161 yods. Compare this with the 161 SLs of the 26-tree;
2. the first seven polygons have 295 yods. Chesed of the 49th TOL is the 295th SL;
3. the first seven polygons & the root edge have 299 yods. Kether of the 49th TOL is the 299th SL;
4. the first 12 polygons & the root edge have 550 yods and 91 vertices (from a formal, mathematical point of view, the endpoints of the root edge count as vertices). CTOL has 550 SLs and 91 TOLs.Any set of five polygons with N corners will have a yod population obeying the formula S(N) = 6N + 5 for the number of SLs in the N-tree because
Σ (6n+1) = 6Σ n + 5 = 6N + 5,
set setwhere
N = Σ n
set
is the number of corners of the five polygons. Therefore, it is not surprising that the yod population of the first five polygons obeys this formula. However, what is interesting is that this set of polygons has 26 vertices, where 26 is the number value of YAHWEH, and 161 yods, which is the number of SLs in the 26-tree. Allowed numbers of overlapping TOLs in the last column are is the number of corners of the five polygons. Therefore, it is not surprising that the yod population of the first five polygons obeys this formula. However, what is interesting is that this set of polygons has 26 vertices, where 26 is the number value of YAHWEH, and 161 yods, which is the number of SLs in the 26-tree. Allowed numbers of overlapping TOLs in the last column are shown ticked. The thick lines separate one set of seven polygons & the root edge from the other set. The running total number of yods should be read upwards, starting from the base in each case.
What is even more interesting (in fact, remarkable) is that the seven polygons and the root edge have the same number of yods as there are SLs in the 49-tree, which maps the 49 subplanes of the seven planes of the cosmic physical plane! The four yods of the root edge therefore denote Kether, Chokmah, Binah and Daath of the 49th TOL. What is most interesting of all is that there exists a subset of the 14 polygons that — together with the root edge — have not only 91 vertices symbolizing the 91 TOLs of CTOL but also 550 yods that denote their 550 SLs. That subset is the set of the first 12 polygons and the root edge. This is amazing, for even if it were coincidence that a set of polygons can be found that contains 550 yods when the root edge is included, it is highly implausible that they would by chance possess 91 vertices as well! Nor is it plausible that it could be just coincidence that the number of SLs in the 49-tree is equal to the number of yods in the root edge and all seven polygons of the Inner TOL.
Twelve of the 14 polygons collectively encode the self-replication of a single TOL into CTOL as a map of all levels of reality. These 12 enfolded polygons have 67 corners (65 outside the root edge) and 76 corners and centres of 88 tetractyses. This is how the respective numbers of Binah, ADONAI and YAHWEH ELOHIM prescribe the polygonal encoding of CTOL (the complete prescription by all Godnames is given in Article 41). Moreover, only this particular combination of polygons has such a property, because only the triangle and square have the necessary seven vertices that must be excluded from
11
the 96 corners of the 14 polygons to leave 91 corners, including the two endpoints of the root edge. As will be now proved, if the three other possible orderings of the 14 polygons are considered:
1. triangle–dodecagon–triangle–dodecagon;
2. dodecagon–triangle–dodecagon–triangle;
3. dodecagon–triangle–triangle–dodecagon,none of them has a yod population that, including the root edge, fits the formula 6N + 4 for N overlapping TOLs with N greater than 91.
Proof of uniqueness of encoding of CTOL in the (7+5) polygons
The two possible orderings: triangle–dodecagon and dodecagon–triangle create (2×2=4) possible combinations of the two sets of polygons. Those not considered earlier are:
1) Triangle–dodecagon
The section: triangle–octagon encodes 76 overlapping TOLs (Fig. 11), which is allowable, although uninteresting, being less than the 91 TOLs of CTOL. The section: triangle–decagon encodes the 86-tree, which is disallowed because it only makes sense to look for a number of overlapping TOLs as a complete map of all levels of reality. The n-tree is always part of N overlapping TOLs, where N>n.
2) Dodecagon–triangle
The section: dodecagon–hexagon encodes 36 overlapping TOLs, which is permissible, but uninteresting, being less than 91. The section: dodecagon–square encodes the 95-tree, which is disallowed for the reason given above. CTOL is encoded in the section: dodecagon–pentagon.
3) Dodecagon–dodecagon
The two sections: dodecagon–hexagon & dodecagon–octagon encode, respectively, 36 & 76 overlapping TOLs, which are both uninteresting. The section: dodecagon–decagon encodes the 86-tree, which is disallowed.Although combination (2) is the only one that encodes a number of overlapping TOLs as large as that in CTOL, it also encodes 36 overlapping TOLs in one set of polygons. This is not permitted, because it is only meaningful for a set of polygons encoding as many TOLs as CTOL to have subsets encoding groups of TOLs that are part of CTOL, not separate, overlapping groups. In the 12-polygon section: triangle–pentagon considered earlier, it encodes not only a single number (91) of overlapping TOLs but also the 26-tree and the 49-tree, which are both parts of CTOL. It is concluded that, of the four possibilities, only this section is permitted.
We conclude that the encoding of CTOL in this particular set and ordering of 12 polygons is unique. (En passim, it is worth noting that the triangle and square uninvolved in this encoding have 44 yods — a very 'Pythagorean' feature in view of the importance of the Tetrad to this philosophy! It is another example of how the Tetrad Principle formulated in Article 12 governs properties of TOL).
In Theosophical terms, the 26th TOL in CTOL maps the fifth subplane of the fourth (Buddhic) plane, counting in both cases from the lowest plane and subplane of each plane. Malkuth of the 26th TOL is Tiphareth of the 25th TOL, which is the centre of the seven TOLs mapping the fourth plane, the central one of the seven planes. Malkuth of the 26th TOL is the pivotal centre of the 49-tree — its 'half-way point,' so to speak. These 26 TOLs corresponding to the first five polygons denote the region of CTOL that is the counterpart of 26-dimensional space-time predicted by
12
13
quantum mechanics for the one-dimensional objects that physicists call 'bosonic strings.' Because of this correspondence between the dimensions of space-time and the lowest 26 subplanes of consciousness, the 26-tree embodies scientific information about strings. CTOL itself is analogous to the superstring because holistic systems embody the same parameters, albeit with different meanings.
Encoded in the seven polygons is the 49-tree representing the 49 subplanes of the seven planes of the cosmic physical plane. They correspond to the 49 triangles at the centre of the Cosmic Tetractys that symbolize Sephiroth of Construction. Each corner of one set of seven polygons denotes a solar subplane and each corner of the five largest polygons in the other set denotes a subplane of the six cosmic, superphysical planes. One endpoint of the root edge denotes the 49th subplane and its other endpoint symbolizes the lowest subplane of the second cosmic plane. The three vertices of the triangle signify the three lowest physical subplanes (called in Theosophy the 'dense physical' subplanes) and the four vertices of the square signify the four highest
14
physical subplanes (known in Theosophy as the four 'etheric' subplanes). The seven vertices of the triangle and square denote the seven subplanes of the physical plane. Enfolded, they have five vertices. This is an example of a 5:7 pattern that is characteristic of seven-fold, holistic systems. An example is the fact that the seven tone intervals of each of the seven types of musical scales include five whole tone intervals. This pattern is the geometrical manifestation of the fundamental distinction between the five Sephiroth of Construction belonging to the Lower Face of the Tree of Life and the two Sephiroth of Construction (Chesed and Geburah) that are part of its Upper Face.
Enfolded, the (7+5) polygons have 67 corners (Fig. 12). This is the number value of Binah, the Sephirah at the head of the Pillar of Judgement that embodies the archetype governing the basic forms of holistic systems. Remarkably, it is the number of yods below Binah of the 1-tree when its 19 triangles become tetractyses. ELOHIM, the Godname of Binah with number value 50, prescribes the (7+5) separate polygons because their 89 sectors have 101 corners, where 101 is the 50th odd integer after 1. They are prescribed by YAHWEH, Godname of Chokmah with number value 26, because 101 is the 26th prime number. It is also the number value of Michael, the Archangel of Tiphareth. The (7+5) enfolded polygons have 65 corners outside their shared root edge, showing how ADONAI, the Godname of Malkuth with number value 65, prescribes their outer form. The 87 sectors of the enfolded (7+5) polygons have 76 corners, where 87 is the number value of Levanah, the Mundane Chakra of Yesod, and 76 is the number value of YAHWEH ELOHIM, the Godname of Tiphareth (see Article 4 in ref. 1 for how the Godnames of the other Sephiroth prescribe the (7+5) polygons).
What other evidence indicates that the 12 polygons encoding CTOL constitute a holistic system, as indicated by the way in which the number values of the ten Sephiroth in the four Worlds parameterize their properties? Converted into tetractyses, their 87 sectors contain 494 yods (Fig. 13). 247 yods lie on the sides of the 48 tetractys sectors of the seven separate polygons of the Inner TOL. This means that (2×247=494) yods line the 192 sides of the 96 tetractyses making up both sets of seven polygons. Of these, 110 yods are corners of the latter, leaving 384 hexagonal yods on their sides. Many previous articles have demonstrated that this number is a parameter of holistic systems. For example, it is the number of corners, lines & triangles surrounding the centres of both sets of seven separate polygons. It is also the number of lines and broken lines in the 64 hexagrams of the I Ching table, as well as the number of yods in CTOL up to the top of the seventh TOL, i.e., the number of yods needed to construct from tetractyses the map of the physical plane. The Pythagorean integers 1, 2, 3 & 4 express the number 494 as:
11 21 31 41
12 2 2 32 42
13 23 33 43
14 24 34 44They also express the 30 yods in the missing triangle and square because
30 = 12 + 22 + 32 + 42.
EL ChAI, the Godname of Yesod with number value 49, prescribes the (7+5) enfolded polygons because they have 490 (=49×10) yods outside their root edge. Their 87 sectors have 165 sides, where
165 = 12 + 32 + 52 + 72 + 92.
Such simple, mathematical beauty is characteristic of holistic systems.
The 295 yods in the seven separate polygons of the Inner TOL symbolize the 295 SLs up to Chesed of the 49th TOL. The four yods in the separate root edge denote Kether, Chokmah, Binah & Daath of the 49th TOL. The 251 yods in the five other polygons of the set of 12 symbolize the 251 SLs in CTOL above the top of the 49-tree (Fig. 14). There are 183 SLs on each side pillar of CTOL and 184 SLs on its central pillar. There are 99 SLs on each side pillar of the 49-tree and 101 SLs on its central pillar, where 101 is the 26th prime number and the number value of Michael, the Archangel of Tiphareth. Hence, there are (183–99=84) SLs on each side pillar above the 49-tree and (184–100=84) SLs on the central pillar down to its top. There are 15 SLs on each side pillar of the 7-tree, which is analogous to the 49-tree because both correspond on their own levels to the Sephirah Malkuth, as well as 17 SLs on the central pillar of the 7-tree. Hence, there are (99–15=84) SLs on each side pillar of the 49-tree above the 7-tree and (100–16=84) SLs on its central pillar below the top of the 49-tree down to the top of the 7-tree. This SL, the 47th from the bottom of CTOL, is the 168th SL on the central pillar, counting from the top of CTOL. 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth. This is remarkable evidence that the 7-tree does, indeed, represent Malkuth. Furthermore, there are (84+84=168) SLs on the side pillar above the 49-tree, which, too, represents this Sephirah on a greater cosmic level. The 504 SLs down to the top of the 7-tree consist of 168 SLs on each side pillar and 168 SLs on the central pillar. This 168:168:168 division will prove to be highly significant when CTOL is compared in the next section with
15
the Sri Yantra. Here is a clear manifestation in the map of physical and superphysical reality of what many previous articles have demonstrated to be the structural parameter of the E8×E8 heterotic superstring. This is, of course, not a coincidence, for the basic unit of matter is a holistic object as well, being the microscopic manifestation of the universal blueprint of the Tree of Life and other sacred geometries.
More evidence that the 49-tree is the cosmic Malkuth level of CTOL is provided by its geometrical composition. The numbers of triangles, their sides & their corners in n overlapping TOLs are given by:
Number of corners = 6n + 4.
Number of sides = 16n + 6.
Number of triangles = 12n + 4.
Number of corners, sides & triangles = 34n + 14.49 overlapping TOLs have (34×49 + 14 = 1680) geometrical elements. This is the number of yods in 168 tetractyses, where 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth. Here is unambiguous evidence for the 49-tree representing the cosmic physical plane. The number 1680 is the number of helical turns that the Theosophist C.W. Leadbeater counted in each whorl of the UPA, the basic unit of matter made visible by his special form of remote viewing ability that is one of the yogic siddhis3 (Fig. 15). Many previous articles have
identified this particle as the E8×E8 heterotic superstring, whose unified interaction is transmitted by 496 gauge bosons. As we shall discover in the next section, when all their triangles are tetractyses, 49 overlapping TOLs have 496 yods on the Pillar of Equilibrium, where 496 is the number of Malkuth. Such a conjunction of number values of the same Sephirah cannot, plausibly, be due to chance. Instead, the Tree of Life map of the cosmic physical plane embodies the superstring structural parameter 1680 because they are both the Malkuth aspect of the Tree of Life and therefore are parameterized by the number value of the Mundane Chakra of this Sephirah.
4. The Sri Yantra represents CTOL
The equivalence of the Tree of Life and the Sri Yantra (Fig. 16) was demonstrated in Article 35.4 It will therefore not be pursued here. The Sri Yantra is generated from nine primary triangles (Fig. 17).

Five downward-pointing triangles symbolizing the feminine, creative energy of the Goddess Shakti intersect four upward-pointing triangles symbolizing the masculine, creative energy, popularly conceived in India as the God Shiva. Their overlapping generates 43 triangles. 42 triangles arranged in four layers of eight, ten, ten and 14 triangles surround a downward pointing triangle whose corners denote the triple Godhead, or Trimûrti, of Shiva, Brahma and Vishnu. At its centre is a point, or 'bindu,' representing the Absolute, or transcendental unity. Including its square enclosure and two sets of circumscribing lotus petals, the Sri Yantra has nine levels.
16
Figure 18. The Sri Yantra is equivalent to CTOL as a map of all levels of reality.
17
There are two ways of conceiving the set of 43 triangles. The more common one is to regard them as lying in the same plane, so that outward-pointing vertices of triangles touch either the bases or vertices of triangles in the adjacent, surrounding set. When their geometrical composition is analysed, this means that the vertices of some triangles meet at a single point in this plane, whilst other vertices lie on edges of triangles. The other way is to regard the Sri Yantra as a three-dimensional stack of four layers of triangles, so that only triangles in the same layer touch one another. As this possibility is the easier one to study, it will be examined first. This will be followed by a discussion of what difference it makes to regard the Sri Yantra as drawn in a plane. Each triangle can be considered either as single triangles, tetractyses or as divided into its three sectors as Type A triangles, Type B triangles, etc. Here, we will consider the 42 triangles surrounding the central one as Type A, each with 19 yods, and arranged in four layers. The central triangle has a special status and will be regarded as a simple triangle without sectors.
Table 3. Yod composition of the three-dimensional Sri Yantra with Type A triangles.
on edges
centres of tetractysesBindu Central triangle Subtotal 1st layer 2nd layer 3rd layer 4th layer Subtotal Total
Table 3 displays the vertices, the hexagonal yods on edges of tetractyses and the hexagonal yods at their centres, as well as the total number in each layer of triangles. There are 129 corners of triangles surrounding the central bindu point. This shows how YAHWEH SABAOTH, the Godname of Netzach with number value 129, prescribes the geometry of the Sri Yantra. Including the separate bindu point, the total number of vertices is 130, where
The 42 triangles have 126 sectors with 126 corners. This number is the sum of the values of all possible different combinations of the letters of EHYEH, the Godname of Kether:
AHIH = 21
A = 1, H = 5, I = 10.
AH + AI + HI + HH = 42
AHI + AHH + HIH = 47
AHIH = 21
Total = 126This shows how EHYEH prescribes the Sri Yantra. A more obvious prescription is the fact that the number 42 is the 21st even integer. The number 126 has the remarkable property that it is the arithmetic mean of the first 26 triangular numbers:
where Tn (= ½n(n+1), the sum of the first n integers) is the nth triangular number. This shows how YAHWEH with number value 26 prescribes the shape of the Sri Yantra.
The total number of yods in the 43 triangles is 760 = 76×10. This shows how YAHWEH ELOHIM, the Godname of Tiphareth with number value 76, prescribes the Sri Yantra. There are 504 yods in the first three layers. There are also 504 hexagonal yods on the 252 edges of the 126 tetractyses making up the 42 triangles surrounding the central one. The first three layers have 336 such yods (168 in each half) and the fourth has 168 such yods. This 168:168:168 pattern is similar to that found earlier for the 168 SLs on each pillar of CTOL above the 7-tree. However, a more interesting pattern is shown in Fig. 18. The 504 hexagonal yods on edges of tetractyses comprise 252 hexagonal yods arranged as three sets of 84 on
18
the 126 edges of the 42 triangles and 252 hexagonal yods arranged as three sets of 84 on the 126 edges of the 126 tetractyses inside them. The former correspond to the 84 SLs on each of the three pillars of the 49-tree down to the top of the 7-tree and the latter correspond to the three sets of 84 SLs above the 49-tree. The exterior and interior of the 42 triangles represent the two sets of 42 TOLs above the 7-tree. They are analogous to each other because they map the two sets of 42 corresponding subplanes above the seven subplanes of the physical plane.
Let us next suppose that the central triangle is a Type B triangle with 46 yods. They correspond to the 46 SLs in the 7-tree below its apex — the 504th from the top of CTOL. This is how the 43 triangles of the three-dimensional Sri Yantra represent the 550 SLs of CTOL. The central triangle represents the physical universe at the centre of the spiritual cosmos mapped by the 504 hexagonal yods on edges of tetractys in the 42 triangles. The seven corners of the nine tetractyses in the former can be thought as symbolizing the seven TOLs mapping the physical plane. and the 84 corners of the 42 triangles can be regarded as symbolizing the 84 TOLs above the 7-tree.
The Godname YAHWEH prescribes the Sri Yantra because Table 4 shows that it contains 260 (=26×10) vertices, sides & triangles when the central triangle is a simple triangle and the 42 triangles are Type A:
Table 4. Geometrical composition of the three-dimensional Sri Yantra.
Bindu Central triangle Subtotal 1st layer 2nd layer 3rd layer 4th layer Subtotal Total
In an analogous way, the seven enfolded polygons of the Inner Tree of Life have 260 yods outside their shared root edge when their 47 sectors are tetractyses (Fig. 19). The Godname YAHWEH SABAOTH with number value 129 prescribes the Sri Yantra because the 43 triangles have 129 sides. They have 87 vertices, where 87 is the number value of Levanah, the Mundane Chakra of Yesod.55. The five Platonic solids represent CTOL
It can be proved mathematically6 that five, and only five, equal-sided polyhedra can exist in three-dimensional space. They are the tetrahedron, octahedron, cube, icosahedron and dodecahedron (Fig. 20).
They are known as the five 'Platonic solids,' so-called not because they were discovered by the Greek philosopher Plato (428/427 B.C.E.–348/347 B.C.E.), as the Pythagoreans knew of their existence long before Plato, but because of the special emphasis he placed upon them in expounding Pythagorean cosmology in his book entitled Timaeus (c. 360 B.C.E.), wherein they were first described.
Formulae for calculating the numbers of triangles, their corners & sides needed to construct the faces of a Platonic solid are listed below:
Formulae
C = number of vertices; E = number of edges; F = number of faces; m = number of sectors of a face. Number of corners of triangular sectors = V = C + F.
Number of sides of triangular sectors = e = E + mF, where m = 3 (tetrahedron, octahedron &19
icosahedron), m = 4 (cube) and m = 5 (dodecahedron).
Number of triangular sectors = T = mF.Table 5 lists the geometrical composition of the faces of each Platonic solid, the first four Platonic solids and all five Platonic solids.
Table 5. Geometrical composition of the faces of the Platonic solids.
Comments
1) ELOHIM, the Godname of Binah with number value 50, prescribes the five Platonic solids with 50 vertices and 50 faces. Their 180 triangular sectors have 100 corners, where
10 10
10 10 10
10 10 10 10.2) 550 geometrical elements are needed to construct the 50 faces of the five Platonic solids, where
550 = 10×55 = 10×
8 9
5 6 7
1 2 3 4= 100
80 90
50 60 70
10 20 30 40.500 (=50×10) more elements are needed to turn the 50 points in space denoting their vertices into regular polyhedra, showing further how ELOHIM prescribes them. This representation of the number 550 demonstrates how the number 10, the Decad, called by the ancient Pythagoreans 'All complete' and regarded by them as the perfect number, determines the SL population of CTOL. The sum of the topmost three numbers is 270; this is the number of sides of the 180 triangles in the five Platonic solids. The sum of the next three numbers is 180, which is the number of triangles. The sum of the last four numbers on the base of the tetractys is 100, which is the number of corners of the 180 triangles:
Indeed, subsets of these three sets of numbers refer to either the first four Platonic solids or all five solids:
20
The Decad determines the 180 triangles in the five Platonic solids because 180 yods surround the centre of a Type B dodecagon — the tenth regular polygon and the last of the seven regular polygons making up the inner form of the Tree of Life (Fig. 21). As 12 = 4×3, the 12 sectors of the dodecagon form three cross-shaped arrays, each containing 60 yods. They denote the 60 triangles in the tetrahedron, octahedron & cube, the 60 triangles in the icosahedron and the 60 triangles in the dodecahedron.
As has been pointed out in a number of previous articles, the dodecagon is the single polygonal form of the Tree of Life. This is why it embodies a parameter that characterizes an archetypal geometrical system such as the five Platonic solids. This 60×3 factorisation of the parameter 180 of holistic systems is encountered in the polyhedral Tree of Life — the disdyakis triacontahedron — as the 60 edges of each type (AB, BC & AC) joining its three types of vertices A, B & C, as will be discussed in the next section. It occurs also in the 60 non-stop/start codons in human mRNA, whose structure is a holistic pattern. Figure 22 displays in detail the correspondence between the 180 yods and the 180 triangular sectors in the faces of the five Platonic solids.7
The simplest polygon — the triangle — can be thought to determine the 368 geometrical elements in the first four Platonic solids because a Type B triangle has 46 yods, which generate the number (4×46=184) of geometrical elements in each half of these regular polyhedra when weighted with the Pythagorean Tetrad (Fig. 23). The number 46 is the average number of geometrical elements needed to construct the faces in each half of the first four Platonic solids. Genetically speaking, this is the human diploid number, i.e., the number of chromosomes in the human cell.
3) The first four Platonic solids are constructed from 248 corners & sides of 120 triangles, where
i.e., 120 is the sum of the first ten odd integers after 1, showing how the Decad determines how many triangles are needed to construct the faces of the solids whose shapes were believed by the ancient Greeks to be those of the particles of the four elements Earth, Water, Air & Fire. The Tetrad also determines the number 120 because it is the sum of the squares of four integers spaced four units apart, starting with the Tetrad, 22 = 4. The number 248 is the number value of Raziel, the Archangel of Binah, and the dimension of the superstring gauge symmetry group E8. This confirms the basic ancient insight that the first four Platonic solids embody the physics of matter, although not of course for the reasons
21
given by Plato in his Timaeus. They have 68 corners (30 polyhedral vertices, where 30 = 12 + 22 + 32 + 42), and 180 sides (60 polyhedral edges). The holistic parameter 180, which was earlier encountered as the 180 sectors in the faces of the five Platonic solids, reappears in the first four Platonic solids as the number of sides of their 120 triangular sectors.
E8 has eight simple (or zero) roots and 240 non-zero roots. Comparing this with the 248 corners & sides in the 38 faces of the first four Platonic solids, Table 5 indicates that the number 8 appears three times, namely, as the eight corners of the 12 sectors in the tetrahedron, as the eight corners at the centres of the faces of the octahedron and as the eight corners of the cube. Rather than try to answer the question of which polyhedron embodies the corners corresponding to the simple roots, let us just note that the 120 sectors in the 38 faces have 60 corners and 180 sides, i.e., 240 corners & sides. They correspond to the 240 non-zero roots of E8. The 180 sides comprise 12 sides that belong either to the tetrahedron, the octahedron or the cube and 168 other sides, where 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth. The latter comprise 78 sides of the 60 sectors of the first three solids and 90 sides of the 60 sectors of the icosahedron. This is remarkable because it reproduces the number values of Cholem and Yesodoth:
However, it is unsurprising, as this division always manifests in holistic systems, as has been demonstrated in many previous articles. The counterpart of the 240 non-zero roots of E8 in the 38 faces of the first four Platonic solids are the 60 corners, the 12 unspecified sides and the 168 other sides, i.e., 72 corners & sides and 168 sides, totalling 240 corners & sides. The former correspond to the 72 roots of E6, the rank-6 exceptional subgroup of E8 and the latter correspond to the 168 roots of E8 that are not also roots of E6.
4) When the 60 sectors of the 12 pentagonal faces of the dodecahedron are turned into tetractyses and the 90 sectors of the 30 internal triangles formed by its centre and edges are turned into tetractyses, 550 hexagonal yods are generated.8 Plato regarded this regular solid as representing the celestial sphere because it resembled the perfect shape of a sphere more than any other one. We now see that not only do the five Platonic solids represent CTOL but so, too, does the fifth one by itself! Each hexagonal yod in the 150 tetractyses needed to construct the dodecahedron symbolizes one of its 550 SLs. The holistic parameter 550 embodied in all five Platonic solid manifests in the last one as well.
6. The disdyakis triacontahedron represents CTOL
The faces of the Platonic solids are regular polygons with the same shape and size. The 13 Archimedean solids have faces with the shapes of two or more regular polygons. Interchanging vertices and faces generates their duals — the 13 Catalan solids. The Catalan solid with the most vertices is called the "disdyakis triacontahedron." Article 239 proved that this polyhedron is the outer form of the polyhedral version of the Tree of Life and all its equivalent sacred geometries (its inner form — the polyhedral counterpart of the polygonal Inner Tree of Life — is a
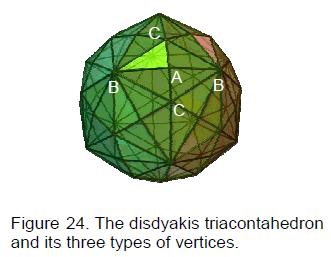
polyhedron with 74 vertices, 216 edges & 144 faces). The disdyakis triacontahedron (Fig. 24) has 62 vertices, 180 edges and 120 triangular faces, that is, 362 geometrical elements make up its faces. Including its centre, there are 363 elements, where 363 is the number value of SHADDAI EL ChAI, the complete Godname
22
23
24
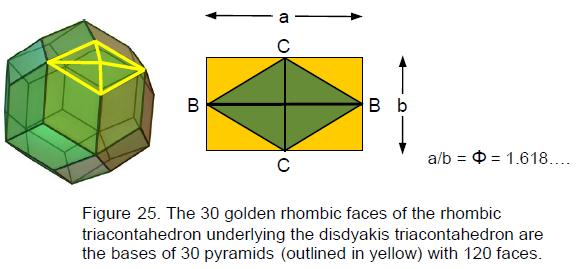
of Yesod. The vertices are of three kinds: the 12 B vertices are vertices of an icosahedron, the 20 C vertices are vertices of a dodecahedron and the 30 A vertices are vertices of rhombic pyramids stuck on the 30 faces of a rhombic triacontahedron (Fig. 25). They are in fact golden rhombic faces because the ratio of their two diagonals (the edges of the underlying icosahedron and dodecahedron) is the Golden Ratio φ. This means that the bases of all the diamond-shaped facets of the disdyakis triacontahedron have this aesthetically pleasing proportion used for centuries by artists and architects.
F is present in this polyhedron in a more subtle way. Imagine a straight line passing through two opposite C vertices. It will be referred to as the C-C axis. As there are 20 C vertices, there are ten different C-C axes. For present purposes, however, only one need be considered. The 60 vertices (30 A, 12 B & 18 C) surrounding a C axis are arranged in 15 sheets or layers. They are the corners of seven polygons either above or below the central plane, which have six vertices arranged at the corners of a hexagon. Table 6 lists the rectangular coordinates of all 62 vertices. Each is a function of F, the distances between adjacent polygons being an integer power of F.
Figure 26 displays the positions of polyhedral vertices plotted in the XY plane with the C axis along the Z axis. It shows that each of the 15 polygons has corners that are polyhedral vertices of the same type. This means that none of their 60 sides are edges of the disdyakis triacontahedron. Moreover, if the sectors of the polygons are Type A triangles, i.e., themselves divided into three triangles, only the centre of the central hexagon and the internal sides of its six sectors (shown red in Fig. 27) are shared with the 180 ordinary triangles inside the polyhedron formed by its centre and its 180 edges. The centres of the 14 polygons above and below the central polygon, the edges of their sectors and the sides of the three triangles in each sector of a polygon are unshared with the polyhedron, as are the 24 internal sides of the 18 triangles in the sectors of the central Type B hexagon. The two opposite C vertices on the Z axis are unshared with the polygons. Including these, the number of unshared geometrical elements is shown below:
triangles
60×3=180 Total = 180 = 550. There are 550 such elements, shown in detail in Fig. 27. They consist of 76 vertices, 294 sides & 180 triangles, i.e., 474 sides & triangles, where 474 is the number value of Daath ("knowledge") and 76 is the number value of YAHWEH ELOHIM, the Godname of Tiphareth. There are 256 vertices & triangles, where 256 = 44, showing how the Tetrad expresses this number. Remarkably, the 180 triangles and the 370 vertices & sides correspond to the 180 triangles and the 370 vertices & sides making up the 50 faces of the five Platonic solids (see Table 1). Indeed, the same 180:370 division appears in the tetractys representation of the number 550 discussed in Section 5:
The 548 unshared geometrical elements other than the two opposite C vertices are the counterpart of the 548 SLs between the apex and nadir of CTOL, the C vertices playing the role of the latter. The disdyakis triacontahedron is the polyhedral representation of CTOL, the unshared geometrical elements of its 15 polygons corresponding to SLs.
The central hexagon has (6×3=18) unshared triangles with six unshared corners and (6×4=24) unshared sides surrounding its centre. The 14 polygons above and below the central hexagon have 14 unshared centres and (60–6=54) unshared corners of (180–18=162) unshared triangles with (294–24=270) unshared sides, i.e., 500 (=50×10) geometrical elements unshared with the internal triangles of the disdyakis triacontahedron. This shows how ELOHIM, the Godname of Binah with number value 50, prescribes the 14 polygons. Each set of seven polygons has 250 unshared elements. Including the two C vertices, 251 elements are either above or below the central hexagon, which has (6×8=48) unshared elements (one corner, four sides & three triangles per sector). 48 is the number value of Kokab, the Mundane Chakra of Hod. Hence, the eight polygons making up the lower half of the disdyakis triacontahedron have (251+48=299) unshared geometrical elements, 251 unshared elements being above the central hexagon.
25
In terms of the correspondence with the 550 SLs of CTOL, this is remarkable, for there are 299 SLs up to the top of the 49-tree mapping the seven planes of consciousness and 251 SLs in the 42 TOLs above it! What this means is that the 48 geometrical elements in the central hexagon that are unshared with the disdyakis triacontahedron are the counterpart of the 48 SLs above the lowest SL in CTOL up to Chesed of the eight Tree of Life. This is the 49th SL prescribed by EL ChAI, the Godname of Yesod, whose meaning "foundation" is appropriate, given that the 25 tree levels up to this point in CTOL signify the 25 spatial dimensions of the physical universe. In correlating geometrical elements in the 15 polygons with SLs, we have to start counting from the lowest C vertex, which signifies the lowest SL of CTOL, proceed to the central polygon, counting 48 more unshared elements that correspond to the next 48 SLs, and then count the 250 elements in the lower set of seven polygons. The 299 elements in the lower half of the polyhedron correspond to the 299 SLs up to the top of the 49-tree that maps the cosmic physical plane. The 251 geometrical elements in the remainder of the polyhedron correspond to the remaining 251 SLs in the 42 TOLs that map the 42 subplanes of the six cosmic superphysical planes, the topmost C vertex denoting the top of the 91st TOL.
As the seven cosmic planes correspond to the seven Sephiroth of Construction, the cosmic physical plane is the 'Malkuth' level of CTOL. We found mathematical confirmation of this earlier. Additional evidence comes from analyzing the yod composition of the eight Type B polygons making up the lower half of the disdyakis triacontahedron, whose 299 unshared corners, sides & triangles are the counterpart of the 299 SLs in the 49-tree. Table 7 shows that the eight polygons have 351 hexagonal yods, where 351 is the number value of Ashim, the Order of Angels assigned to Malkuth.
351 is the sum of the first 26 integers, showing how YAHWEH, the Godname of Chokmah with number value 26, prescribes the eight types of polygons formed by vertices of the disdyakis triacontahedron. They have 385 yods other than vertices, where
385 =
22 32
42 52 62
72 82 92 102.This demonstrates how the Decad determines the number of new yods needed to construct the eight Type B polygons from tetractyses. They have 495 yods surrounding their centres. As
495 = 9×55 = 32×(12+22+32+42+52) = 32 + 62 + 92 + 122 + 152,
the Godname YAH with number value 15 prescribes the yod population of these polygons. It also prescribes the 470 (=47×10) yods in their 99 tetractyses that are not polyhedral vertices, as 47 is the 15th prime number. All 15 polygons have 135 vertices and 780 hexagonal yods (that is, ten times the number of hexagonal yods in the central hexagon), totalling 915 yods. 900 yods surround the 15 centres, where 900 = 302 = (12+22+32+42)2 = 9×102 = 32(1+2+3+4)2 = (3+6+9+12)2. This illustrates the Tetrad Principle at work in expressing the mathematical properties of holistic systems, for 900 is the square of the sum of the squares of the first four integers. Including the two opposite C vertices, there are 137 vertices. This shows how the disdyakis triacontahedron embodies the number 137 central to atomic physics because its reciprocal is almost equal to the fine-structure constant α = e2/ħc. Its origin remains one of the unexplained mysteries of theoretical physics. Not so in sacred geometry. It arises in particle physics because it is a parameter of all sacred geometries, and subatomic particles and their interactions are the physical manifestation of these equivalent blueprints in the microscopic world. It is the electromagnetic force measured by the number 137 that determines the electronic configurations of atoms and hence the chemical properties of the elements.
26
Including the C vertex, there are 504 yods in half the polyhedron (Table 7 & Fig. 28). There are 496 yods other than centres of its eight polygons. This is the number value of Malkuth, the last Sephirah of the Tree of Life denoting its physical form. The very half of the polyhedron whose 299 geometrical elements are analogous to the 299 SLs of the 49-tree mapping the cosmic physical plane embodies the number value of the Kabbalistic name of the Sephirah that is associated with this section of CTOL! Such an amazing property refutes the suggestion that it might be merely coincidence that there are 550 geometrical elements in the 15 Type B polygons and the two opposite C vertices, quite apart, of course, from the equally remarkable 299:251 division in elements that compose the polygons in one half of the polyhedron and its remainder. Another piece of evidence that discounts the possibility of coincidence is the fact that 66 corners of tetractyses surround the centres of the eight polygons in half the polyhedron. As 66 is the 65th integer after 1, this property is aptly prescribed by ADONAI, the Godname of Malkuth with number value 65.
According to Table 7, including a C vertex, the number of yods in the seven polygons either above or below the central hexagon with 91 yods is 413. Including the two C vertices, the number of yods in the 15 polygons = 2×413 + 91 = 917. 916 yods surround the centre of the disdyakis triacontahedron. The number of yods on the central Pillar of Equilibrium of n overlapping TOLs constructed from tetractyses is given by
N(n) = 10n + 6.10
Hence, N(91) = 916. The number of yods surrounding the centre of the disdyakis triacontahedron is exactly equal to the number of yods that lie on the central pillar of CTOL when its 1096 triangles are tetractyses! Here is further, spectacular evidence that this polyhedron is the polyhedral counterpart of CTOL. The geometrical elements composing the 15 polygons perpendicular to a C-C axis correspond to SLs between the apex and nadir of CTOL, whilst their yods correspond to yods lying on its central pillar.
The number of yods on the central Pillar of Equilibrium of the n-tree (the lowest n TOLs in CTOL) is given by
N(n) = 10n + 10.11
Hence, N(49) = 500. There are four more yods up to, but not including, Daath of the 50th TOL. The 504 yods in the eight polygons (including the C vertex) correspond to the 504 yods on the central pillar of CTOL up to this SL. Its significance is that it is the next lower SL after Binah of the 50th TOL, where 50 is
27
the number value of ELOHIM, Godname of Binah, and that this SL is the 248th from the top of CTOL, where 248 is the dimension of E8, the rank-8, exceptional Lie group describing the symmetries of the unified interaction between superstrings of either ordinary matter or what physicists have called 'shadow matter' (invisible matter that interacts with the former only gravitationally). As N(49) = 496, 49 overlapping TOLs mapping the cosmic physical plane have 496 yods on the central pillar. This shows how EL ChAI, the Godname of Yesod with number value 49, prescribes the dimension 496 of the two Lie groups SO(32) and E8×E8 describing the unified interaction between superstrings Each such yod denotes one of the 496 spin-1 gauge bosons responsible for the forces between them. It is yet more evidence for the 49 overlapping TOLs mapping the
cosmic physical plane being the Malkuth level of the CTOL. Four yods are added by replacing them by the 49-tree, above which are four more yods up to Daath of the 50th TOL. This is analogous to the 496 yods (including the C vertex) that surround the eight centres of the polygons in one half of the disdyakis triacontahedron (see Table 7). To be consistent, however, with the earlier finding that the 15 polygons and two C vertices have 917 yods, we have to interpret the number 916 as the number of yods other than the top C vertex, rather than the number of yods surrounding the centre of the polyhedron. This is because the number 504 includes the latter. So the lowest eight Type B polygons and the lowest C vertex denote the 504 yods on the Pillar of Equilibrium up to (but not including) Daath of the 50th TOL, the lowest C vertex denoting the
lowest SL in CTOL, the 495 yods that surround the centres of the eight polygons in the lower half of the disdyakis triacontahedron representing the next 495 yods on the central pillar of 49 overlapping TOLs, their eight centres denoting the eight yods either added by the conversion of the former into the 49-tree or lying on the central pillar above the top of the 49-tree as far as (but not including) Daath of the 50th TOL. The remaining 412 yods in the seven polygons above the centre of the polyhedron denote the 412 yods on the central pillar from Daath of the 50th TOL to the top of CTOL.
The Tetrad and the Godname ELOHIM with number value 50 determine the number 916 because
28
where 229 is the 50th prime number. The number 229 is a geometrical parameter of the seven enfolded polygons of the Inner Tree of Life, being the number of edges of their 141 triangles when they are Type B polygons.12 It is also a parameter of the seven enfolded Type A polygons, being the number of yods associated with each set of their 47 tetractyses other than the 34 polygonal corners that are not also centres of other polygons (Fig. 29), i.e., 'pure' corners.
The factorisation of 916 as 4×229 has a remarkable meaning vis-à-vis the Kabbalistic representation of the four Worlds of Atziluth, Beriah, Yetzirah & Assiyah as four overlapping TOLs (Fig. 30). Being a map of all levels of reality, it is equivalent to CTOL. The number of pure corners of the 28 polygons enfolded on each side of the Pillar of Equilibrium = 4×66 = 264. This is the number of yods in one set of seven enfolded polygons (Fig. 31). As the seven enfolded polygons enfolded in each TOL have 229 yods other than pure corners, the number of such yods associated
with each set of 28 enfolded polygons making up
29
the inner form of four overlapping TOLs = 4×229 = 916. This is the number of yods lying on the Pillar of Equilibrium of CTOL. Different representations of the same holistic system are always parameterized by the same set of numbers.
The counterpart in the Sri Yantra of the 504 SLs in CTOL down to the top of the 7-tree mapping the physical universe are the 504 hexagonal yods lying on the sides of tetractyses in the 42 triangles. They consist of 252 hexagonal yods on the outer sides of these triangles (three sets of 84) and 252 hexagonal yods (three sets of 84) inside them. They symbolized the 84 SLs in each of the three pillars of CTOL down to the top of the 49-tree and the 84 SLs in each of the three pillars below the top of the 49-tree down to the top of the 7-tree. What is the counterpart of this
3×84:3×84 pattern in the 504 yods (including the upper C vertex) in the eight polygons in the upper half of the disdyakis triacontahedron? Figure 32 shows that 84 yods other than corners surround the centre of each of the three six-sided polygons. 84 yods other than corners surround the centres of two triangles, 84 yods other than corners surround the centres of two more triangles, leaving 84 yods made up of the C vertex, the yods in the last triangle and the corners & centres of all eight polygons. That particular triangle has been chosen only for illustration, for it is not obvious which triangle should be included with the corners and centres. Whichever is the correct one is irrelevant to what is demonstrated here, namely, that the 504 yods in the 15 polygons (including the C vertex) naturally and simply divide into six sets of 84 yods, as should be expected if the disdyakis triacontahedron embodies a map of all superphysical .levels of reality that is analogous to CTOL.
The same pattern exists in the distribution of 504 yods that surround the centre of a Type C dodecagon (Fig. 33). Pairs of opposite sectors contribute 84 yods. The 84 light and 84 dark yods symbolize, respectively, the 84 SLs on the Pillar of Mercy above the 49-tree and between the 7-tree and the 49-tree. The light and dark green yods denote the corresponding SLs on the Pillar of Equilibrium and the light and dark blue yods denote the corresponding SLs on the Pillar of Judgement. As the last regular polygon of the Inner TOL, the dodecagon is the single polygonal counterpart of the Tree of Life. This is demonstrated by the fact that the 60 hexagonal yods in a Type A dodecagon are analogous to the 60 hexagonal yods in
30
the Tree of Life itself when its 16 triangles are tetractyses (Fig. 34). Only this polygon can have such a number of hexagonal yods. Its Tree of Life character is the reason why 168 yods are needed to turn it into a Type B dodecagon and why 504 yods are needed to convert it to a Type C dodecagon. The former correspond to the 168 SLs on the central pillar of CTOL down to the top of the 7-tree mapping the physical universe. The extra 2×168 yods correspond to the 168 SLs on each side pillar (this is an alternative to the representation in Fig. 33 of the 504 SLs).
As we have seen, the 168:168:168 division of SLs distributed on the three pillars of CTOL above the 7-tree is characteristic of holistic systems. It was encountered in Article 4313 in the discussion of the {3,7} tessellation of the 3-torus mapping the 168 automorphisms of the Klein quartic as the 168 hexagonal yods on the edges of its 56 triangles when they are tetractyses and as the 336 hexagonal yods added, generating 504 hexagonal yods, when the sectors of these triangles are tetractyses. The geometry of the tessellated 3-torus was shown to be analogous to the Tree of Life, embodying its parameters.
The number 504 and its 168:336 division is embodied arithmetically in the Tree of Life for the following reason: assigning the 70 odd integers after 1 to its 70 yods generates the number 5040 because
712 – 1 = 3 + 5 + 7 +... + 141 = 5040.
This is the number of yods in 504 tetractyses. There are 40 yods above the Lower Face. Assigning the first 40 odd integers after 1 to them generates the number 1680 because
412 – 1 = 3 + 5 + 7 +... + 81 = 1680.
This is the number of yods in 168 tetractyses. This means that the 30 integers 83-141 assigned to the 30 yods in the Lower Face add up to 3360, which is the number of yods in 2×168 tetractyses. The distinction between the Lower Face and the rest of the Tree of Life creates in an arithmetic way the 168:2×168 division characteristic of holistic systems. It is remarkable that this purely geometrical distinction divides the 70 yods into precisely the sets of 40 and 30 yods that generate this division when the odd integers after 1 are assigned to them. It is an example of the beautiful harmony between number and geometry displayed by sacred geometries. It manifests in the three uppermost whorls of the UPA shown in Fig. 15, which C.W. Leadbeater described as thicker than the lower seven ones, each whorl being a helix with 1680 circular turns. As the microscopic manifestation in space-time of the Tree of Life, the three whorls correspond to the Supernal Triad of Kether, Chokmah & Binah, whilst the seven other whorls correspond to the seven Sephiroth of Construction.
_________________________________References
1 Phillips, Stephen M. Article 4: "The Godnames prescribe the inner Tree of Life," (WEB, PDF), p. 6.
2 Phillips, Stephen M. Article 1: "The Pythagorean nature of superstring and bosonic string theories," Article 1 (WEB, PDF), p. 4.
3 Besant, A. & Leadbeater, C.W.: "Occult Chemistry," Theosophical Publishing House, Adyar, Chennai, India, 1951, p. 23.
4 Phillips, Stephen M. Article 35: "The Tree of Life nature of the Sri Yantra and some of its scientific meanings," (WEB, PDF).
5 See ref. 4 for how other number values of the ten Sephiroth in the four Worlds are present in the Sri Yantra.
6 Proof: Let p = the number of sides of each face (or the number of vertices of each face) and q = the number of faces meeting at each vertex (or the number of edges meeting at each vertex). Then, for a regular polyhedron with C vertices, E edges and F faces, pF = 2E = qC. Substituting these in Euler's formula for a polyhedron:
C – E + F = 2,
2E/q – E + 2E/p = 2,so that
1/q + 1/p = ½ + 1/E.
Since E is positive,
1/q + 1/p > ½.
Allowed values of p and q are p = 3, q = 3 (tetrahedron), p = 4, q = 3 (cube), p = 3, q = 4 (octahedron), p
31
= 5, q = 3 (dodecahedron) & p = 3, q = 5 (icosahedron).
7 Phillips, Stephen M. Article 46: "How sacred geometries encode the 64 codons of mRNA and the 64 anticodons of tRNA," (WEB, PDF), Fig. 38b.
8 See Table 1 in Article 3 (WEB, PDF).
9 Phillips, Stephen M. Article 23: "The polyhedral Tree of Life," (WEB, PDF).
10 Proof: n overlapping Trees of Life have (n+1) Faces. Each of the lowest n Faces has 10 yods on the Pillar of Equilibrium when all triangles are tetractyses and the (n+1)th Face has 6 yods. Number of yods on the central pillar of n overlapping Trees of Life = N(n) = 10n + 6.
11 Proof: the n-tree has (n+1) Faces, each with 10 yods on the central Pillar of Equilibrium. Number of yods on the central pillar of the n-tree = 10(n+1) = 10n + 10.
12 Proof: The seven enfolded polygons have 42 sides. Their 47 sectors have 46 internal sides. When each polygon is Type B, their 47 sectors add (47×3=141) sides. Number of sides of seven enfolded Type B polygons = 42 + 46 + 141 = 229.
13 Phillips, Stephen M. Article 43: "The Tree of Life nature of the {3,7} tessellation of the 168 automorphisms of the Klein quartic on the 3-torus," (WEB, PDF), Table 3.
32