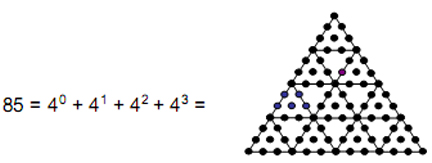ARTICLE 21

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://www.smphillips.mysite.com

Abstract

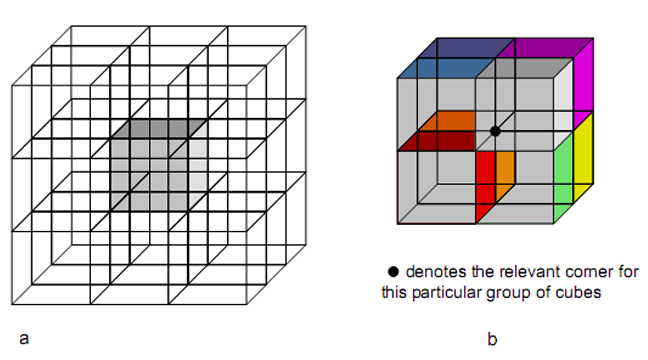
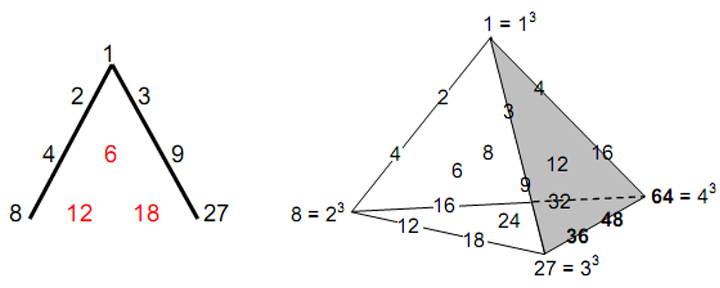
1. The 168 faces

It was shown in Article 20 that the I Ching table (Fig. 1) is a symbolic expression of the 3×3×3 array of cubes shown in Fig. 2a. Each of the upper trigrams of the eight

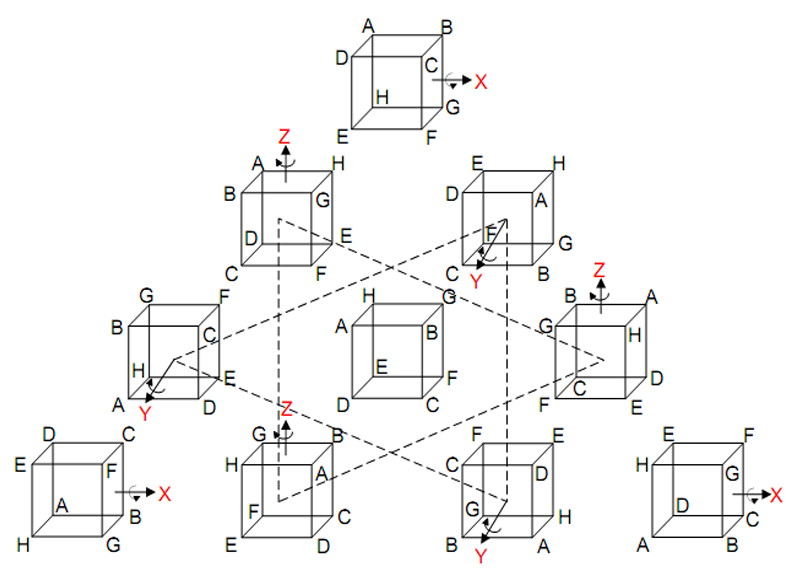
hexagrams along the diagonal of the table symbolises the three cube faces whose intersection defines a corner of a cube. The pairing of each trigram with a different one symbolises an association between the three faces defining a corner of the central cube and the three faces of one of the cubes surrounding it that is contiguous with this corner. Each corner of the cube at the centre of the 3×3×3 array of cubes (the grey one in Fig. 2a) is the point of intersection of the corners of seven other cubes. Three of

Figure 2. Each corner of the grey cube (a) at the centre of a 3×3×3 array of cubes touches three cubes (coloured blue, indigo & violet in (b)) at the same level as itself and four cubes (red, orange, yellow & green) that are either above or below it.

2

these (the violet, indigo and blue cubes in Fig. 2b) are at the same height as the cube and the remaining four (the green, yellow, orange and red ones) are above or below it. Let us express the pattern of eight cubes centred on any corner of the central cube as 

 where ‘1’ always denotes the central cube, ‘3’ denotes the three cubes contiguous with it at the same height and ‘4’ denotes the four contiguous cubes above or below

Figure 3. Three cubes on the same level are contiguous with each corner of the central (grey) cube.

it. As we jump from corner to corner in the top face of the central cube, the L-shaped pattern of three coloured cubes in the same plane rotates (Fig. 3), as do the four cubes above them. Likewise, as we go from corner to corner in the bottom face of the central cube, the three cubes in the same plane change, as do the four cubes below them. Movement through all eight corners of the central cube involves every one of the 26¹ cubes in the 3×3×3 array because they are all contiguous with its

corners.

Each corner of the central cube is the point of intersection of the three orthogonal faces (3) of each of the seven cubes that are contiguous with it (Fig. 4). The number of such faces generating the corners of the central cube is

Counting these corners in the same way as the pattern of cubes, that is, differentiating any corner from the three corners at the same height and the four corners below them, then

where

Therefore,

24 = [(1+3) + 4]×(1_X + 1_Y + 1_Z)

3

where 3_X (≡ 3×1_X) signifies the three faces of cubes that are orthogonal to the X-axis and associated with the three corners at the same height as the corner labelled ‘1’ (and similarly for the Y- and Z-axes), and 4_X (≡ 4×1_X) denotes the four faces orthogonal to the X-axis associated with the four corners below corner ‘1’ (and similarly for 4_Y and 4_Z). Therefore, substituting Equation 6 in Equation 3,

The 168 faces of the 26 cubes surrounding the central cube that touch its eight corners consist of seven sets of 24 faces. Each set consists of the three orthogonal faces of the cube corresponding to corner ‘1’, the seven faces perpendicular to the X-axis at the seven other corners, the seven faces perpendicular to the Y-axis at these corners and the seven faces perpendicular to the Z-axis at these corners. Each group of seven faces comprises a face for each of the three corners of the central cube at the same height as corner ‘1’ and a face for each of the four corners below it. The 24 faces naturally divide into two groups of twelve:

and

Hence,

where

and

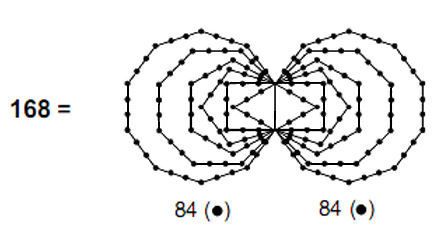
We see that the 168 faces are made up of two distinct sets of 84 faces. Each set comprises 28 faces orthogonal to the X-axis, 28 faces orthogonal to the Y-axis and 28 faces orthogonal to the Z-axis. One set is associated with the four upper corners and the other set is associated with the four lower corners.

Figure 5. There are 168 yods on the unshared sides of the two sets of six polygons, 84 for each set. They symbolise
the two sets of 84 faces of the 26 contiguous cubes that surround the central cube and define its corners.

4

Which set is associated with which group of corners is determined by whether the corner ‘1’ is regarded as an upper or a lower corner of the central cube. If the former, the 84 faces are associated with the lower corners. If the latter, the 84 faces are associated with the upper corners. For the present purpose, no choice needs to be made for ‘1’.

 Figure 6. 84 yods surround the centre of a 2nd-order tetractys.

The pair of 84 cube faces intersecting at the corners of the two opposite faces of the central cube is encoded in the inner form of the Tree of Life (Fig. 5). The first six regular polygons enfolded on each side of the central pillar of the Tree of Life can be divided into tetractyses of ten yods. There are 84 yods on the sides of each set of polygons. Each yod denotes a face, whilst the pair of identical sets of polygons corresponds in the cube to the two sets of four corners that form either a square face or a tetrahedron.

The Pythagorean significance of the number 84 is that the next higher order tetractys — the 2nd-order tetractys (Fig. 6) — is made up of 85 yods, that is, there are 84 yods surrounding its central yod. This means that 84 hidden degrees of freedom (here ambient cube faces) express the concrete form of a holistic system (here, the four corners of a face of the central cube), as symbolised by the yod at the centre of the tetractys, which corresponds to Malkuth of the Tree of Life.

Figure 7. The Klein Configuration of the 168 elements of the group PSL(2,7) of transformations of the Klein quartic. 

The Tetrad Principle² prescribes this number because

that is, 84 is the sum of the squares of the first four odd integers.

2. The Klein Configuration

 Felix Klein (1849–1925) is well-known to mathematicians as one of the nineteenth

5

century’s great geometers. The one-sided, closed surface called the “Klein bottle” is named after him. In 1878, he discovered that the curve

has the 336-fold symmetry of the group SL(2,7). This curve is known to mathematicians as the “Klein quartic.” Klein showed that its Riemann surface is mapped onto itself (hence ‘automorphisms’) by168 analytic transformations. Hurwitz³showed that a compact Riemann surface of genus g≥2 has at most 84(g–1) automorphisms and the same number of anti-automorphisms. A Riemann surface with the maximum number of automorphisms is called a “Hurwitz curve” of genus g (g≥3). A Hurwitz curve of genus 3 has (84(3-1) = 84×2 =168 ) automorphisms. So the Klein curve is the Hurwitz curve with the smallest genus g = 3. Although there is an infinite number of Hurwitz curves⁴, no curves other than the Klein curve with g = 3 and one with g = 7 have equations known to mathematicians.⁵

The Riemann surface of the Klein quartic can be represented by the so-called “Klein Configuration” (Fig. 7). It has168 coloured, hyperbolic triangles and168 grey triangles. Each of the 14 slices shown numbered has 12 coloured triangles. They can be grouped in clusters of seven, each group forming one of 24 heptagons:

This composition can be represented as:

The numbers within each bracket denote the triangles in the two slices of each of the seven sectors of the Klein Configuration. Each sector is made up of two different slices, each with 12 triangles, i.e., the 168 triangles can be sorted into 84 from one type of slice and 84 from the other type:

where

Seven slices of one type have 84 triangles made up of 28 red, 28 yellow and 28 green triangles. The seven slices of the other type have 84 triangles made up of 21 yellow, 21 green, 21 red and 21 cyan triangles.

Let us compare the 7-fold pattern of 24 coloured triangles indicated by Equation 15, each denoting one of the 168 automorphisms of the Klein quartic, with the composition

6

7

(according to Equation 6) of the seven sets of 24 cube faces:

24 = (1_X + 1_Y + 1_Z) + (4_X + 3_X) + (4_Y + 3_Y) + (4_Z + 3_Z).

Compare also the 84 triangles within the seven slices of each type (let us call them ‘A’ and ‘B’) given by Equations 16 and 17 with the two sets of 84 faces given by Equations 10 and 11. The following correspondences exist:

Slice A upper/lower sets of 4 corners

4 red triangles		4 faces orthogonal to X-axis for each corner below/above ‘1’
4 yellow triangles		4 faces orthogonal to Y-axis for each corner below/above ‘1’
4 green triangles		4 faces orthogonal to Z-axis for each corner below/above ‘1’

Slice B 3 corners at same level as ‘1’

3 cyan triangles		3 faces defining a corner (‘1’) of a cube
3 red triangles		3 faces orthogonal to X-axis for each corner at level of ‘1’
3 yellow triangles		3 faces orthogonal to Y-axis for each corner at level of ‘1’
3 green triangles		3 faces orthogonal to Z-axis for each corner at level of ‘1’

We see that the two types of slices in the Klein Configuration correspond to the two opposite faces of a cube. The four corners of a face that include ‘1’ are contiguous with (4×3×7 = 84) faces of surrounding cubes in the 3×3×3 array and correspond to slice B. The four corners of the opposite face are contiguous with (4×3×7 = 84) faces of surrounding cubes and correspond to slice A. The 4:3 splitting of the triangles in the heptagons mirrors the fact that there are four contiguous cubes above or below any given corner of the central cube and three contiguous cubes at the same height. As a cube face is either positive or negative depending on whether it faces the positive or negative direction of a coordinate axis, there is for each of the 

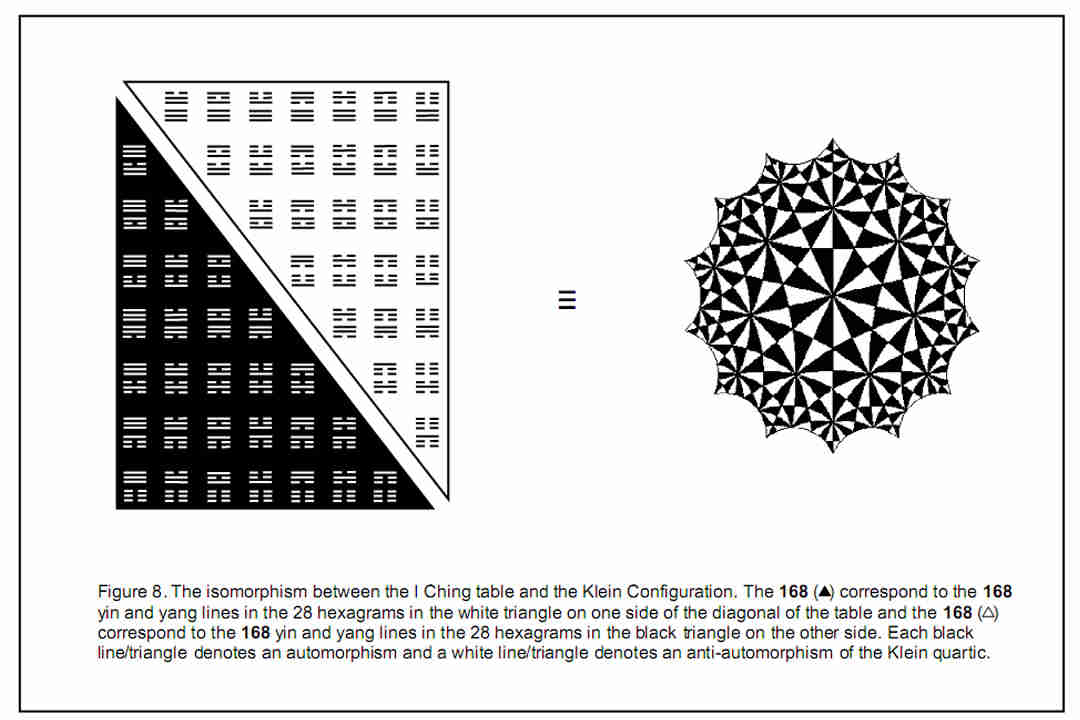
168  faces one of opposite polarity. This means that there are 168  ‘dual’ faces of surrounding cubes contiguous with the eight corners of the central cube that have the opposite polarity. These correspond to the 168  grey triangles in the Klein Configuration that represent the 168  anti-automorphisms of the Klein quartic.

Fig. 8 displays the isomorphism between the 168  automorphisms and the 168  yin/yang lines in the white, triangular half of the I Ching table above the diagonal, as well as the 168  anti-automorphisms and the 168  lines in the black half of the table below the diagonal. Equation 16 indicates that the 168  triangles are made up of coloured types that are multiples of 28, whilst the 168  lines belong to 28 hexagrams. As, according to Equation 6,

 24 = 4_X + 4_Y + 4_Z + (1_X + 3_X) + (1_Y + 3_Y) + (1_Z + 3_Z),

8

168 = 7×24 = 7×[4_X + 4_Y + 4_Z + (1_X + 3_X) + (1_Y + 3_Y) + (1_Z + 3_Z)].

This shows that the 168 faces, likewise, comprise six different types of 28 faces. The splitting of each hexagram into two trigrams corresponds in the 3×3×3 array of cubes to the pair of opposite faces of a cube with four corners (the distinction between 4_X and (1_X + 3_X), etc) and in the Klein Configuration to each of its seven sectors being divided into half. The I Ching table, the 3×3×3 array of cubes that it symbolises and the Klein Configuration are isomorphic to one another. It was argued in Article 20 that the degree of correspondence between the

Figure 10. The 3-torus, in which the Klein map can be embedded, is topologically identical to a cube whose opposite faces are imagined stuck together.

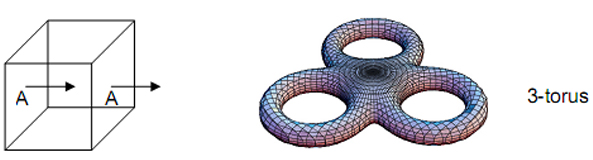
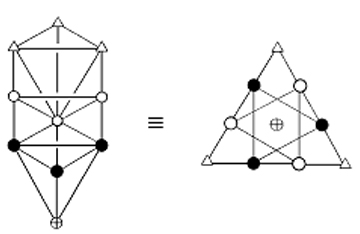
first two is too high to be dismissed as coincidence. The same conclusion applies to the lattermost two.

The 1:3:4 pattern of cubes associated with the central cube corresponds in each sector of the Klein Configuration to the cyan hyperbolic triangle of the

Figure 11. The three rotations of the central cube about the X-, Y- and Z-axes (labelled red) generate a tetractys array of ten orientations with the unrotated cube at its centre.

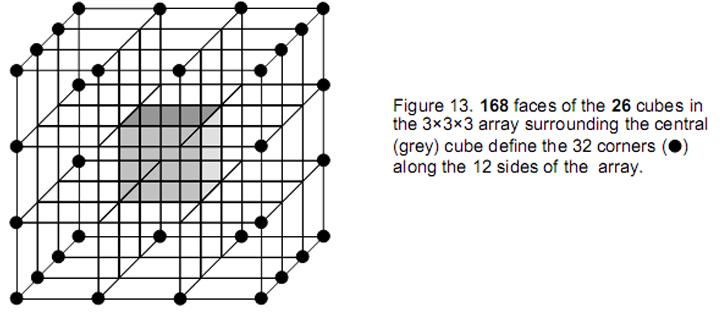
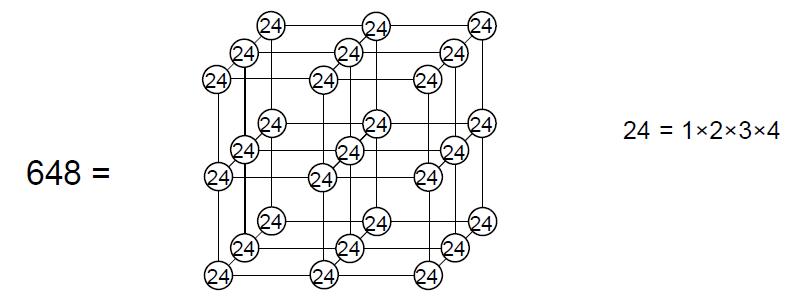
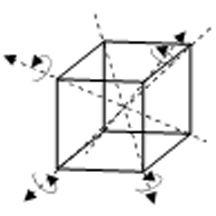
9

central heptagon, the three red, yellow or green triangles in one half of a sector and the four triangles with these colours in the other sector. The existence of this pattern in the archetypal pattern of 27 cubes symbolised by powers of 3 in Plato’s Lambda reflects the pattern of Sephiroth of Construction in the Tree of Life (Fig. 9). ‘1’ represents the starting point (any corner of a cube) and corresponds to Daath (Knowledge), from which objective manifestation emerges. ‘3’ represents the three other corners of a square — the halfway stage in the creation of a cube. They correspond to the triad of Chesed, Geburah and Tiphareth. ‘4’ denotes the remaining four corners of the cube. They correspond to the four-fold emanation of Netzach, Hod, Yesod and Malkuth, which signifies the material aspect of the Tree of Life, the element ‘Earth,’ whose particles the ancient Greeks believed has the form of a cube.

The Klein Configuration can be embedded in a 3-torus because the latter is a compact manifold of genus 3. The 3-torus is topologically equivalent to a cube whose opposite faces are imagined to be glued together (Fig. 10), so that movement along each coordinate axis is periodic, like motion around a circle. This means that all eight corners of a cube represent the same point of a space that has the topology of a 3-torus. However, suppose that they were tagged or labelled in some way that differentiated them. As the cube has three 4-fold axes of symmetry, namely, rotations of 90°, 180° and 270° about the X-, Y- and Z-axes, there are nine possible configurations of labelled corners into which the original one can be rotated, that is, there are ten different configurations of corners connected by these rotations about the coordinate axes. They form the tetractys pattern shown in Fig. 11. The cubes at the corners of the tetractys are the central cube after rotation through 90°, 180° and 270° about the X-axis. The two triads of cubes that are connected by dotted lines are the result of similar rotations about the Y- and Z-axes.

Figure 12. Equivalence of the Tree of Life and the tetractys.

As geometrical representations of the ten-fold nature of holistic systems, the Tree of Life and tetractys are equivalent (Fig. 12). The Supernal Triad of Kether, Chokmah and Binah corresponds to the three points at the corners of the tetractys. The next two triads of Chesed-Geburah-Tiphareth and Netzach-Hod-Yesod correspond to the two triangular arrays of points whose intersection forms a Star of David. Malkuth at the base of the Tree of Life corresponds to the centre of the tetractys. The ten rotational configurations of a cube constitute a Tree of Life pattern because the set of three rotations through 90°, 180° and 270° about an axis perpendicular to a face of the cube (say, the X-axis) corresponds to the Supernal Triad, whilst the pair of three-fold rotations about the Y- and Z-axes corresponds to the pair of triads of Sephiroth of Construction above Malkuth, this being the last Sephirah of Construction that corresponds to the non-rotated cube.

The 3×3×3 array of cubes has (4×4×4=64  ) corners. Within each face of the array itself are four corners, each the meeting point of three faces of each of four cubes. The

10

number of faces defining the corners within the six faces of the array = 6×4×4×3 = 288 = 1¹ + 2 ² + 3 ³ + 4 ⁴. This is another example of the Tetrad Principle expressing properties of mathematical objects that are archetypal. Between the ends of its twelve sides are two corners, each defined by three faces of cubes. Three faces define each corner of the array itself.  

The number of cube faces defining corners along the sides of the array = 3[12×(2+2) + 8] = 3×56 = 168 . This is the same as the number of faces of the 26  cubes whose intersections define the corners of the central cube. They correspond to the 168  grey triangles of the Klein Configuration shown in Fig. 7 that represent the 168  anti-automorphisms of the Klein quartic. Including the (8×3=24) faces that define the eight corners of the central cube, the total number of faces defining the  64  corners of the array = 168  + 288 + 168  + 24 = 648. They consist

Figure 14. Four cubes with 1×2×3×4 assigned to their 27 corners generate the number of faces defining the 64 corners of the 3×3×3 array of cubes.

of (648/3= 216) sets of three perpendicular faces, where 216  = 6³. There are (168 +24=192) faces defining the eight corners inside the array and (288+168  =456) faces defining the 56 corners on its surface. As 192 = 8×24 = 2³×24 and 648 = 27×24 = 3³×24, these two numbers can be represented by an array of four cubes (Fig. 14) with (24=1×2×3×4) assigned to each corner. This is another beautiful illustration of the Tetrad Principle at work in expressing archetypal patterns and the numbers that they embody because four joined cubes with the number 4! at each of their corners generate the number (648) of faces defining the 4³ corners of the 3×3×3 array of cubes, whilst one cube with 4! assigned to each of its 2³ corners generates the number (192) of faces defining the corners of the central cube.

11

4! of these faces belong to the cube itself and 7×4! belong to the 26  cubes surrounding it, where 7 is the fourth  odd integer and 26  is the sum of the first four  Mersenne numbers:

These numbers are also the numbers of combinations of, respectively, one, two, three and four objects, so that 26 is the number of combinations of ten objects arranged in the four rows of a tetractys:

A
B C
D E F
G H I J

Figure 15. The first six enfolded polygons have 24 corners outside their shared root edge. 168 other yods in 35 tetractyses are associated with them.

 square (symbol of the number 4), four to a side:

Articles 17 and 18 showed that the average distances (in 1/10 AU) of the planets Venus-Uranus from the asymptotic centre of the logarithmic spiral-shaped planetary nebula that spawned them are the Bode numbers:

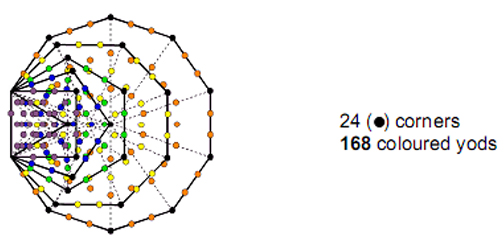
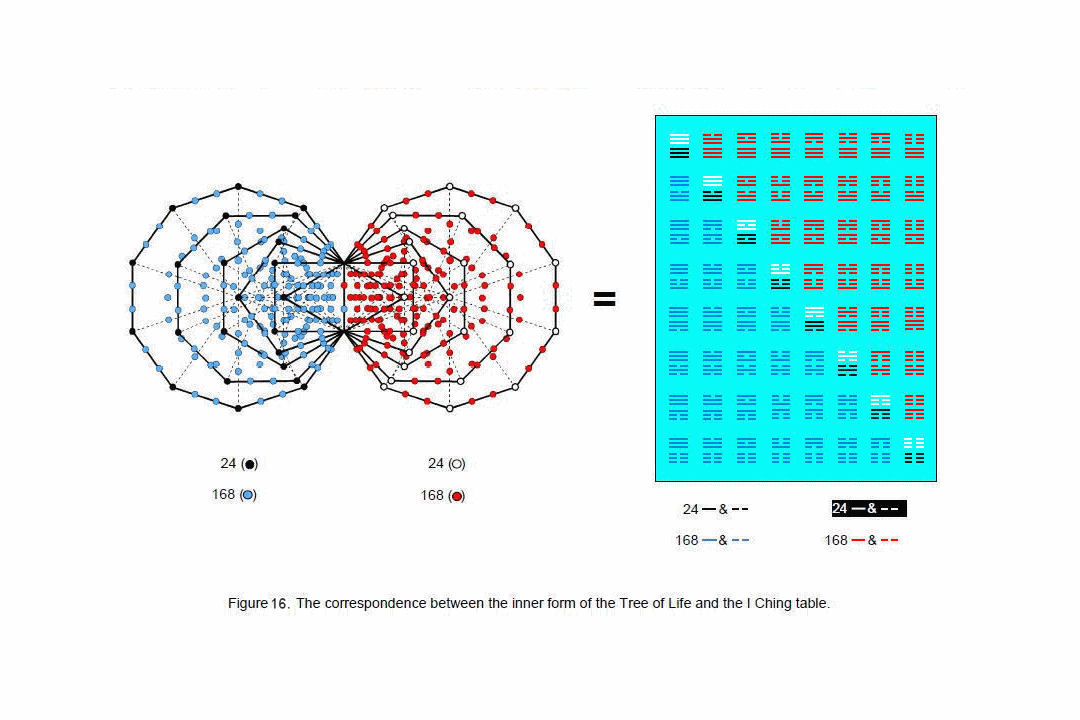
12

13

The average distance of the Asteroids from the asymptotic centre is 24. Uranus, the last member of the first octet of planets, has an average distance of 168  from them. This 24:168  pattern of planetary distances corresponds in the 3×3×3 array of cubes to the 24 faces defining the eight corners of the cube at the centre of the 3×3×3 array of cubes and the 168  faces of the surrounding 26  cubes that, too, define these corners. The fact that the average distance from the asymptotic centre of the last member of the first octet of planets is 192 — the same as the number of faces defining the corners of the central cube and the number of yang or yin lines in the I Ching table — is strong evidence of a non-accidental isomorphism between the Solar System and the 3×3×3 array of cubes. It exists because both the Solar System and the Klein Configuration connected with superstring physics⁶ are holistic manifestations of the same universal design. “As above, so below,” wrote Hermes Trismegistus, the semi-mythical Egyptian teacher of mystical wisdom, at the beginning of his great work The Emerald Tablet.

This is confirmed by the fact that the same  24: 168  pattern is exhibited in the first six enfolded polygons that are part of the inner form of the Tree of Life (Fig. 15). Both sets of six polygons have 336 yods other than corners, two of which lie on their shared side, so that 168  yods can be regarded as belonging to or as associated with each set of polygons, which has 24 corners outside their shared side. The 24:168  pattern found for the faces of the 3×3×3 array of cubes and for the average planetary distances reflects the fact that the cosmic blueprint of the Tree of Life governs both the natural processes that formed the solar system and the physics of superstrings. The Divine Name ELOHIM assigned to Binah in the Tree of Life has the gematria number value 50  . It prescribes this pattern because the two sets of the first six enfolded polygons have 50  corners. The Godname YAHWEH with number value 26  prescribes it because each set of six enfolded polygons has 26  corners. See Article 4 (pp. 4–5) for how all the other Godnames assigned to the Sephiroth prescribe these two sets of six polygons and hence this fundamental pattern.

As discussed in Article 18,⁷  the 24:168  pattern of yods in each set of six enfolded polygons has its counterpart in the I Ching table as the 24 lines of the upper or lower trigrams along the diagonal of the table and the 168  lines of the 28 hexagrams above or below the diagonal (Fig. 16). Each line signifies a face of a cube, it being a yang line if the outward normal to the face points along a positive X-, Y- or Z-axis and a yin line if it is directed along the negative axis.

The cube has 13 axes of symmetry that are of three types:

1. three 4-fold axes (C₄) of rotation of 90°, 180° and 270° (therefore, 3×3 = 9 rotations):

2. four 3-fold axes (C₃) of rotation of 120° or 240° (therefore, 4×2 = 8 rotations):

3. six 2-fold axes (C2) of rotation of 180° (therefore, 6 rotations):

14

4. the identity (one rotation of 360°).

The octahedral group O₃ of order 24 describes the 24 possible rotations of a cube.

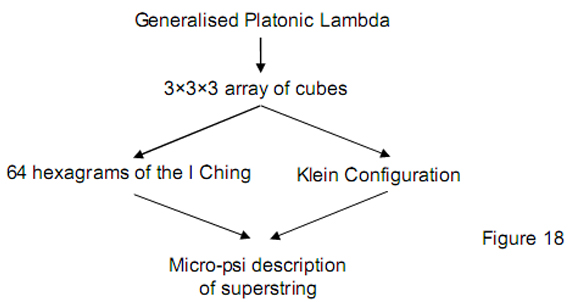
3. Superstring structural parameter 168

It was pointed out in Article 11⁸ that the mathematical pattern through which Plato said in his Timaeus  the Demiurge proportioned the cosmos is incomplete because it involved only the integers 1, 2 and 3, whereas Pythagoras taught that the integers 1, 2, 3 and 4 constituted the fundamental numbers expressing all aspects of the physical and spiritual cosmos. The

Figure 17. Plato’s Lambda and its tetrahedral generalisation.

realisation that his famous ‘Lambda’ is but two sides of a tetractys of integers and that this tetractys is but one triangular face of a tetrahedral array of 20 integers (Fig. 17) has been demonstrated ⁹ to generate the tone ratios of the Pythagorean musical scale in a symmetric way that is absent from the account known to historians of music. Article 20¹⁰ showed that the first four powers of 2, 3 and 4 spaced along the edges of the tetrahedron are the numbers of 0-cubes (points) in the sequence of generation from a point of a cube, a 2×2×2 array of cubes and a 3×3×3 array of cubes.

15

As this article has shown that the 3×3×3 array is isomorphic to the Klein Configuration, we see a remarkable continuity between the mathematical algorithm that Plato said God used to design the universe and the Klein Configuration. This represents the 168  automorphisms of the Klein quartic symbolised by the 168  yang/yin lines of the off-diagonal hexagrams of the I Ching table and by the 168  yods other than corners making up the first six polygons of the inner form of the Tree of Life. Article 15¹¹  made connections between the Klein Configuration and the micro-psi description of the superstring discussed in many earlier articles. The chain of logic linking the generalised Platonic Lambda to the superstring structural parameter 168 is set out in Fig. 18.

Figure 19. Each of the ten whorls of the UPA/superstring described with micro-psi vision by Annie Besant and C.W. Leadbeater is a helix with 1680 turns that twists five times around its axis. Each turn represents a circularly polarised oscillation of a string. There are 84 oscillations in a 90° twist, 168 oscillations in a 180° twist and 336 oscillations in a 360° twist. Each oscillation is the manifestation of one of the 168 automorphisms of the Klein quartic, is symbolised in the I Ching table by a yang or yin line making up the 28 hexagrams on either side of the diagonal and corresponds to one of the 168 faces of the 26 cubes surrounding the cube at the centre of the 3×3×3 array of cubes that intersect at its eight corners. Both the table with 336 off-diagonal lines and the array with 336 faces defining corners either in its surface or of the central cube symbolise one complete revolution of the whorl, that is, a whole cycle.

 

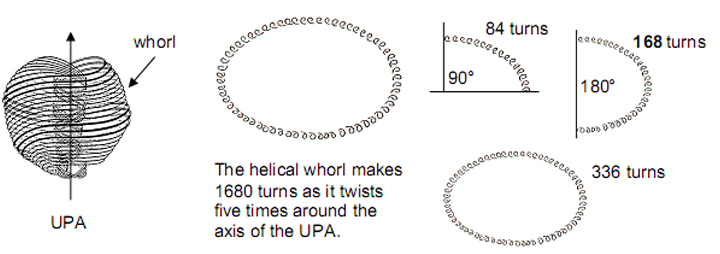
Fig. 19 shows the way in which the helical form of each whorl of the UPA/superstring is represented by the I Ching table and by the Klein Configuration. It demonstrates that the hyperbolic triangles of the Klein Configuration and the yin/yang lines of the I Ching table signify fundamental, physical phenomena manifesting in the subatomic world as circularly polarised oscillations or waves that propagate around the string-like whorls of

Figure 20. Of the 70 corners of the two sets of 7 polygons, three on either side of the shared edge coincide with Sephiroth on the side pillars of the Tree of Life, leaving 32 unshared corners associated with each set that symbolise hexagrams.

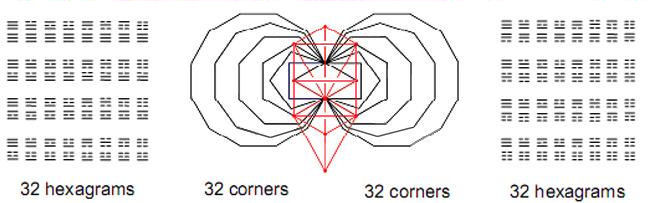
16

the superstring. The 168  yang lines signify the outward half of each revolution and the 168  yin lines represent the movement of a whorl as it completes the full revolution. These two half-cycles correspond in the 3×3×3 cubic array to the 168  faces defining the 32 corners on its exterior (see Fig. 13) and to the 168  faces defining the corners of the central cube. In the inner form of the Tree of Life, they correspond to the two sets of six enfolded polygons (see Fig. 16), each with 168  yods other than corners.

The distinction between the 32 exterior corners of the array and the 32 interior ones is mirrored in the inner Tree of Life as the two sets of seven enfolded polygons, each set having 32 corners other than those coinciding with Sephiroth on the side pillars (Fig. 20). The number 64  is also the number of hexagrams in the I Ching table, which is two sets of 32 hexagrams, one the mirror image of the other (Fig. 1). This bipolarity corresponds to the two similar sets of polygons.

Table 1. Number values of the Sephiroth in the four Worlds.

The first hexagram, Ch’ien (The Creative, Heaven), corresponds to the corner located at Daath and the last hexagram, K’un (The Receptive, Earth), corresponds to the corner located at Tiphareth. As the largest of the integers in the generalised Lambda (see Fig. 17),  64 is the number value of Nogah  (“Glittering Splendour”), the Mundane Chakra of Netzach, the seventh Sephirah, traditionally associated with the planet Venus. In terms of the planetary Bode numbers, 64  is the ratio 192/3, where 192 is the Bode number of Uranus, the last member of the first octet of planets predicted by the author’s theory of the Solar System¹² and 3 is the Bode number of Venus. This corresponds in the I Ching table to the ratio of the number of lines in the first  trigram — the Heaven trigram — to the number of lines in the first 32 hexagrams, the mirror images of which appear in the second set of 32 hexagrams and the 192 lines of which correspond to the difference between the Bode numbers of Pluto (384) and Uranus, i.e., to the average distance between them in units of 1/10 AU.* Finally, 64  is the number of sets of three perpendicular faces whose intersections define the eight corners of the cube at the centre of the 3×3 array.

These examples of the appearance of the gematria number value of a particular Kabbalistic Mundane Chakra in widely diverse and seemingly, unconnected contexts demonstrate that a hidden harmony made visible through number pervades phenomena, whatever their space-time scale. 

* 1 AU (Astronomical Unit) is the average distance of the Earth from the Sun (approximately, 93 million miles), this being defined as the arithmetic mean of its least and furthest distances.

17

This unity, which could have no rational cause if it were the miraculous product of coincidence, exists because these phenomena are all manifestations of the mathematical archetypes of the Divine Mind, which — whether expressed in mystical traditions or in pure mathematics — possess isomorphic features because they embody the same idea.

 References

1. Numbers in boldface are the number values of the Hebrew names of the ten Sephiroth of the Tree of Life, their Godnames, Archangels, Orders of Angels and Mundane Chakras. They are listed above in Table 1. They are calculated by means of the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers associated with its letters.

2. Phillips, Stephen. Article 1: “The Pythagorean Basis of Superstring and Bosonic String Theories,” (WEB, PDF).

3. Hurwitz, A. “Über algebraische Gebilde mit eindeutigen Transformationen in sich,” Math. Ann. 41 (1893), 403–442.

4. Murray Macbeath, A. “On a theorem of Hurwitz.” Proc. Glasgow Math. Assoc. 5 (1961), 90–96.

5. Murray Macbeath, A. “Hurwitz groups and surfaces.” The Eightfold Way. MSRI Publications, vol. 35, 1998, 11.

6. Phillips, Stephen. Article 15: “The Mathematical Connection between Superstrings and their Micro-psi Description: a Pointer towards M-theory,” (WEB, PDF).

7. Phillips, Stephen. Article 18: “Encoding of Planetary Distances and Superstring Structural Parameters in the I Ching Table,” (WEB, PDF), pp. 15–16.

8. Phillips, Stephen. Article 11: “Plato’s Lambda — Its Meaning, Generalisation and Connection to the Tree of Life,” (WEB, PDF).

9. Phillips, Stephen. Article 12: “New Pythagorean Aspects of Music and the Connection to Superstrings,” (WEB, PDF).

10. Phillips, Stephen. Article 20: “Algebraic, Arithmetic and Geometric Interpretations of the I Ching Table,” (WEB, PDF), pp. 19–22.

11. Ref. 6.

12. Phillips, Stephen. Article 17: “The Logarithmic Spiral Basis of the Titius-Bode Law,” (WEB, PDF).

18