
1
1. The Titius-Bode Law
Sir Isaac Newton (1642–1727) showed in his Principia Mathematica that a gravitational force varying as the inverse square of their distance from the Sun binds the planets in orbits that are ellipses (Fig. 1). These curves are characterised by their eccentricities:
e = (1 – b2/a2)½,
where a is the length of the semi-major axis and b is the length of the semi-minor axis. A circle, which has a = b, has zero eccentricity. All the planets have nearly circular orbits, except Mercury with e = 0.21 and Pluto with e = 0.25. Planets revolve in an anticlockwise sense around the Sun situated at one of the two foci of each ellipse.
The distance of each focus from the centre of the planet’s ellipse is ae. Its distance at its closest point A to the Sun is therefore (a – ae) and its distance at its farthest point B is (a + ae). Their sum is 2a, so that the average of these distances is a, the length of the semi-major axis. Unless stated otherwise, it is this average of its largest and shortest distances from the Sun that is meant when the text refers to a planetary distance.
In 1766, the German mathematician, Johan Daniel Titius (1729–1796) of Wittenberg, translated into German “Contemplation de la Nature,” by the French natural philosopher Charles Bonnet. To the paragraph where Bonnet remarks: “We know seventeen planets that enter into the composition of our solar system;* but we are not sure that there are no more,” Titius added what is now known as the ‘Titius-Bode Law’ (or sometimes ‘Bode’s Law’):
“Take notice of the distances of the planets from one another, and recognize that almost all are separated from one another in a proportion which matches their bodily magnitudes. Divide the distance from the Sun to Saturn into 100 parts; then Mercury is separated by four such parts from the Sun, Venus by 4 + 3 = 7 such parts, the Earth by 4 + 6 = 10, Mars by 4 + 12 = 16. However, notice that from Mars to Jupiter there comes a deviation from this so exact progression. From Mars there follows a space of 4 + 24 = 28 such parts, but so far no planet was sighted there. But should the Lord Architect have left that space empty? Not at all. Let us therefore assume
____________________________
* That is, major planets and their satellites.
2
that this space without doubt belongs to the still undiscovered satellites of Mars, let us also add that perhaps Jupiter still has around itself some smaller ones, which have not been sighted yet by any telescope. Next to this for us still unexplored space there rises Jupiter's sphere of influence at 4 + 48 = 52 parts; and that of Saturn at 4 + 96 = 100 parts. What a wonderful relation!”1
The German astronomer, Johan Elert Bode (1747–1826), was putting the finishing touches in 1772 to the second edition of his introduction to astronomy “Anleitung zur Kenntniss des gestimten Himmels,” which he originally published in 1768 at the age of 19, when he came across the relationship proposed by Titius in a footnote to the second edition of his translation. Convinced by it, he added it as a footnote in his text, although only acknowledging Titius as his source in later editions, possibly because of some urging by him.
Despite this plagiarisation of Titius’s discovery, the relationship came to be known as Bode’s Law, although he merely popularized it. In fact, it is not a physical law at all because that status requires a conceptual foundation for what remains merely an empirical relationship between numbers and average planetary distances. Nevertheless, this article will follow contemporary practice by referring to it as the ‘Titius-Bode Law,’ whilst at the same time recognising that it is but a rule.
Titius had noticed that, if 0 were assigned to Mercury, 3 to Venus, 6 to Earth, 12 to Mars, etc, that is, 3 times successive powers of 2, and then 4 added, the resulting integers when divided by 10 were approximately equal to the average distances of the planets then known from the Sun in terms of the Sun-Earth distance:
Mercury
Venus
Earth
Mars
Asteroids
Jupiter
Saturn
Uranus
Neptune
Pluto
0
3
6
12
24
48
96
192
384
768
Add 4: 4
7
10
16
28
52
100
196
388
772
Divide by 10: 0.4
0.7
1.0
1.6
2.8
5.2
10.0
19.6
38.8
77.2
The division by 10 enables the distances to be compared with that of the Earth, whose distance from the Sun is about 93 million miles, or one Astronomical Unit (AU).*
One way to help visualize the relative sizes in the Solar System (Fig. 2) is to imagine a model in which it is reduced in size by a factor of a billion. Then the Earth is about 1.3
____________________________
* The exact figure is 149,597,871 Km.
3
cm in diameter (the size of a grape). The Moon orbits about a foot away. The Sun is 1.5 metres in diameter (about the height of a man) and 150 metres (about a city block) from the Earth. Jupiter is 15 cm in diameter (the size of a large grapefruit) and 5 blocks away from the Sun. Saturn (the size of an orange) is 10 blocks away; Uranus and Neptune (lemons) are 20 and 30 blocks away. A human on this scale is the size of an atom; the nearest star would be over 40,000 km away.
Table 1 indicates that the distances of the planets from the Sun show good agreement with those predicted by the Titius-Bode Law as far as Uranus but fail for the next two planets, Neptune and Pluto.
Planet Mercury Venus Earth Mars Asteroids Jupiter Saturn Uranus Neptune Pluto It was first tested in 1781 when William Herschel discovered Uranus at a distance predicted by the relationship. It was accepted by astronomers until the discovery of Neptune in 1846. It is interesting that some of the larger asteroids between Mars and Jupiter satisfy the law. This indicates that the Asteroid Belt is likely remnants of the proto-planetary nebula that failed to form a planet. Ceres, discovered by G. Piazzi on January 1, 1801, is the largest asteroid and the first to be discovered. It comprises over one-third of the total mass of all the asteroids and has a distance from the Sun of 2.77 AU, which compares with the predicted value of 2.8 AU. The larger asteroids have distances that spread about this figure. The asteroid Kleopatra shows the best agreement with the Titius-Bode Law with a distance of 2.793 AU. One object in the Asteroid Belt, Chiron, discovered in 1977, is anomalous in that its orbital period of 50.7 years is much larger than typical asteroid periods of 3–5 years, whilst its mean distance from the Sun is 13.63 AU, which compares with their typical values of 2–3 AU. Because it is emitting super-volatiles, it could not have been in its present orbit for very long. It is thought likely to be an intruder from a much colder region outside the Solar System — probably a comet from the Kuiper Belt — rather than a remnant of a planet between Mars and Jupiter that broke up. This is further suggested by its possession of a coma, which asteroids do not have.
According to the Titius-Bode Law, the mean distance in Astronomical Units from the Sun of the nth planet from Mercury can be written:
dn = 0.4 + 0.3×2n-1 (n = 1, 2, 3, … 9) (1) 4
= 4 + 3×2n-1×1. where 0.4 is Mercury’s mean distance from the Sun. What astronomers have failed to notice in Equation 1 is that it can be expressed wholly in terms of the set of four integers 1, 2, 3 & 4, as Equation 2 indicates. These integers are symbolised by the rows of dots in the tetractys symbolising for the Pythagoreans the perfect number 10:
1
2
3
4
This is the first clue to what until now has been the complete mystery of the mathematical regularity observed by the mean distances from the Sun of planets other than Neptune and Pluto. Indeed, it was the absence of any credible theory underlying the law that made many astronomers dismiss the excellent agreement between the numbers as a series of lucky coincidences when they found that it broke down for the two outermost planets. However, their displays of professional scepticism have been neither convincing nor unified. The Titius-Bode Law has remained an enigma, often mentioned in books on astronomy with a mixture of scientific reserve and curiosity that conceals a measure of embarrassment about what to make of a simple, numerical regularity that is suggestive far more of a designing Creator than of what the force of gravity might have produced if it had acted on a fledgling Solar System subject only to Newtonian mechanics and the rule of chance!
It is important to point out that the number 10 used as a divisor in the Titius-Bode Law is the number in the sequence of integers starting with 4 that corresponds to the planet Earth. It is what turns this term in the sequence into 1, making comparison of planetary mean distances simpler when they are expressed in Astronomical Units. Presumably, a hypothetical Martian astronomer discovering this empirical relationship would have divided these integers by 16 in order to make a convenient comparison with the distances of the planets measured in terms of his Astronomical Unit — the Sun-Mars mean distance. Similarly, a Venusian astronomer would have divided them by 7 and a Jovian astronomer would have used the divisor of 52 to make comparison easier. As the correct explanation of the rule cannot, of course, be expected to favour any particular planet by having one of these numbers as the divisor in its mathematical formulation, it is clear that the procedure of dividing every integer by 10 is both parochial in an astronomical sense and unnecessary in a theoretical sense, because only human astronomers would want to make this division in order to ease comparison between the actual and predicted numbers. It is only the relative proportions of the numbers in the sequence that matter, not their absolute values, which only become actual distances when a particular planet is arbitrarily chosen to set the unit of distance. A true explanation of the rule must not discriminate between planets and will need to explain only the ratios of the set of integers: 4, 7, 10, 16. 28, 52, 100, etc, not their absolute magnitudes, which have been used to express a relationship in a way that favours a particular planet, namely, Earth. That said, a remarkable connection exists, as already mentioned, between the terrestrial formulation of the rule and what the author has found to be the universal mathematical lexicon expressing numbers with cosmic significance, namely, the Pythagorean mathematical formulation of whole systems in terms of the integers 1, 2, 3 & 4. This gives unique significance to the mathematical formulation of the Titius-Bode law in terms of the Sun-Earth mean distance, for these integers do not appear when the rule is expressed in terms of any other planet’s distance from the Sun.
5
Another point that must be made at this stage is that, by assuming that its conventional form has to apply to all the planets, astronomers have introduced an unnecessary complication into the Titius-Bode equation:
dn = (4 + 3×2n-1)/10. (3) It is counter-intuitive to require n = –∞ so that d1 = 0.4 for Mercury, when n is a positive integer for all other planets. As it appears in Equation 3, the value of n signifies the order of location of the planet from Mercury. What is so special about Mercury that it should be differentiated in this radical way from the other planets? It should have been obvious that Equation 3 holds (in theory, that is) for all planets except Mercury because the first term is already the distance of Mercury from the Sun, whilst n = 1 corresponding to Venus. Equation 3 needs to be modified or at least be understood in a new way that makes sense (if there is any) of the special mathematical status attributed for Mercury by requiring n = –∞. People may have been reluctant to create a new mystery by not letting the equation apply to Mercury, as though this was tantamount to saying that this planet disobeyed the Titius-Bode Law, thereby discrediting its historical status as a genuine regularity observed by all the planets except Neptune and Pluto. However, this is not the logical implication of allowing the values of n to start only with 1. Like it or not, it is distances of planets that are measured from Mercury — not from the Sun — that increase by successive, integer powers of 2. The canonical formulation of the Titius-Bode Law appears to give to Mercury a special status in making its distance simply an added constant in Equation 3 that is falsely taken into account by bizarrely requiring n = –∞ for this planet. As we shall see, however, this is an illusion arising from the fact that the planetary average distances stem from other distances defined by the underlying theory. One cannot let n = 0 for Mercury and change the added constant in Equation 3 from 0.4 to 0.25 so that d0 = 0.4 because this would reduce all ensuing values by 0.15, significantly worsening the agreement for Venus, Earth, the Asteroid Belt and Jupiter, although marginally improving it for Mars, Saturn, Uranus, Neptune and Pluto. The natural meaning of n as the number signifying the order of a planet from the Sun becomes lost if — as it is often written — the power of 2 in Equation 3 is n, not n–1, because Venus is then the case n = 0, so that n denotes the order in the sequence of planets counting from Venus. This makes even less sense in terms of a fundamental theory of planetary distances than counting from Mercury because it attributes a false theoretical significance to what is merely the second planet!
The form of the Titius-Bode Law that has to be explained is not its normalised, canonical form but the equation for the distance (measured in arbitrary units) of the (n+1)th planet from the Sun:
dn+1 = 4 + 3×2n-1, (4) where n = 1 applies to Venus, i.e., the value of n refers to the nth planet beyond Mercury. Equation 4 can also be written as
4 + 3/2×2n = 1 + 3/2(21 + 2n) = 1 + (1 + 21)(21 + 2n)/2 [1 + (21 + 22)/2] + (2n + 2n+1)/2. Mercury’s distance is the first term (shown in square brackets), the second component of which ((21 + 22)/2) has the same form as the second term in Equation 5 representing the distance between Mercury and the nth planet after it. Indeed, for n = 1 (Venus), the latter is merely a repetition of it. This shows that Mercury at least belongs to the same mathematical pattern as the other planets, which is certainly not what requiring n = –∞ for this planet suggests! However, (21 + 22)/2 cannot be treated as the first term in a
6
geometric progression involving successive powers of 2 because, as was just stated, the second term associated with Venus is exactly the same. As (20 + 21)/2 = 3/2>1, the first component, 1, cannot be split up into an analogous expression without introducing a negative component, -½, which lacks meaning in the context of distances from the Sun. This may be regarded as an argument against the existence of an unseen planet between the Sun and Mercury, which would require n to assume negative values if (as seems reasonable) it, too, obeyed the Titius-Bode Law. If, instead, the number ‘1’ denoted its distance from the Sun, the next two expressions for the mean distance of Mercury and Venus from the Sun would correctly be (1 + 3×20 = 4) and (1 + 3×21 = 7). However, the distances of planets beyond Venus would then have to be (1 + 3×2n-1) instead of (4 + 3×2n-1), which leads to unacceptably more inaccurate, predicted values. Therefore, a hypothetical planet between Mercury and the Sun does not restore mathematical generality to the Titius-Bode Law in an acceptable way.
Although it would not persuade astronomers, another powerful argument against the possibility of the existence of such an unobserved planet is that it would imply the existence of eleven heliocentric planets,1 which would violate the Pythagorean view of the Solar System as a whole system modelled on the archetypal, ten-fold tetractys. As we shall see shortly, although one principle determines the relative sizes of all planetary average distances, its mathematical expression takes two forms; the transition from one to the other corresponds to the changeover from Uranus to Neptune — the first planet to exhibit serious deviation from the Titius-Bode Law. In fact, the analysis predicts that this departure is an illusion. By so doing, it proves that Pluto is a true planet.
2. The Pythagorean musical scale
Any musical scale is defined by its starting note — the tonic C, with a tone ratio of 1 — and its finishing note — the octave C', with a tone ratio of 22. In the Pythagorean scale, the arithmetic mean of these tone ratios: (1 + 2)/2 = 3/2 defines the tone ratio of the ‘perfect fifth’ G, so-called because it is the fifth note in the Pythagorean scale (Fig. 3).
The pitch interval between the perfect fifth and the octave is 2/(3/2) = 4/3, which defines the tone ratio of the fourth note F, the so-called ‘perfect fourth.’ Descending a perfect
____________________________
1This includes the Asteroid Belt, which is the remains of a planet that failed to form.
2 The tone ratio of a musical note is the ratio of its frequency to that of the tonic.
7
fourth from G creates the second note D, the major second, with a tone ratio of (3/2)×(3/4) = 9/8. An ascent from D by a perfect fifth then creates A, the major sixth with a tone ratio of (9/8)×(3/2) = 27/16. Stepping down a perfect fourth generates E, the major third with a tone ratio of (27/16)×(3/4) = 81/64. Ascending by a perfect fifth from this note creates the last note B in the scale, the major seventh, with a tone ratio of (81/64)×(3/2) = 243/128. The perfect fifth thus divides C and C' into all other notes.
The first seven notes of the Pythagorean scale:
are repeated on each higher or lower octave, corresponding notes, respectively, increasing or decreasing in pitch by a factor of 2. The octave is spanned by five whole tone intervals of 9/8 and two ‘leimmas’ of 256/243, which correspond to (but are 10% flatter than) the modern, equal-tempered semitone: (9/8)5×(256/243)2 = 2.
Table 2 shows the tone ratios of the first eleven octaves of the Pythagorean musical scale. The last column shows the running total of overtones — notes above the tonic with tone ratios that are integers. Notice that the first nine overtones in purple cells:
3, 6, 12, 24, 48, 96, 192, 384, 768,that are successive octaves of a perfect fifth include the very integers that Titius noticed denote the distances (when divided by 10) of the (then known) planets from Mercury. This is the second clue to the Pythagorean basis of the Titius-Bode Law.
Table 2. The Tone Ratios of the Pythagorean Musical Scale.
of
Overtones768, the perfect fifth of the tenth octave, is not, however, the distance of Pluto from Mercury and so it needs to be explained why, instead, 384, the perfect fifth of the ninth octave, denotes its distance and how (if at all) Neptune fits into the sequence of overtones.
3. Perimeter of ellipse
As pointed out in Section 1, the mean distances of the planets from the Sun are equal to the lengths of the semi-major axes of their elliptical orbits. Any law of scaling of the former is therefore also one of the latter. Indeed, being a characteristic of orbits, it is really this length, not the artificial notion of ‘mean distance,’ that is fundamental. The area of an ellipse with semi-major axis a and semi-minor axis b is πab, that is, a simple,
8
algebraic function of a and b. This is not the case with its perimeter. For an ellipse with eccentricity e, the perimeter P is
P = 4aE(e), where
is the complete elliptic integral of the second kind.2 This cannot be expressed as a simple algebraic function, so mathematicians have worked out various approximations. An exact, series expansion for P in ascending powers of e is3:
= 1 – (1/4)e2 – (3/64)e4 – (5/256)e6 – (175/16384)e8 – (441/65536)e10 – … . Notice that this converges to the correct limit 1 of a circle as e → 0.
An astoundingly accurate formula approximating P was given in 1918 by the Indian mathematical genius, S. Ramanujan (1887–1920)4:
P ≈ π(a+b)[1 + 3h/(10 + √(4–3h))],
All the terms match the correct series (9) up to and including the coefficient of e18! It is amazingly accurate for small e and, even when e ≈ 1, the absolute size of the relative error is only 7π/22 – 1, or about 4×10–4.
Table 3 shows how accurately — even for Pluto, the planet with the largest eccentricity — the circumferences of the planetary orbits approximate to the value 2πa for a circle:
Planet e
P/2πa
Mercury 0.21
0.988882
Venus 0.01
0.999975
Earth 0.02
0.998999992
Mars 0.09
0.997972
Jupiter 0.05
0.999375
Saturn 0.06
0.999099
Uranus 0.05
0.999375
Neptune 0.01
0.999975
Pluto 0.25
0.984187
The level of approximation is far better than that between measured planetary distances and those predicted by the Titius-Bode Law. This means that the discrepancies cannot
9
be due merely to considering their orbitals as circles instead of as ellipses, otherwise Mars with the largest eccentricity amongst the planets Venus-Neptune might be expected to show the worst agreement, which it does not.
The very accurate proportionality between a, the mean distance of a planet from the Sun, and its orbital circumference implies that the latter, starting with Venus, increases as integer powers of 2 in accordance with the Titius-Bode Law, although not exactly. It raises the possibility that circumferences of planetary orbits may be more relevant to the understanding of the Titius-Bode Law than the artificial notion of an arithmetic average of their maximum and minimum distances from the Sun. As explained in Section 6, however, this turns out not to be the case.
4. Undertones, tones & overtones
In Timaeus, his treatise on cosmology, Plato (428 B.C.E.–347 B.C.E.) described how the Demiurge measured the substance of the World Soul according to the simple proportions of the first three powers of 2 and 3, which came to be represented by what is known as ‘Plato’s lambda’ because of its resemblance to the Greek letter Λ (Fig. 4).5 This came to be recognised as but two sides of a tetractys array of ten integers whose ratios determine the tone ratios of the notes of the Pythagorean scale:
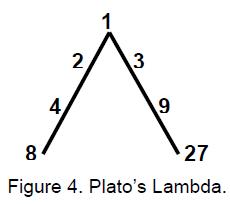
The way in which they generate the spectrum of musical notes is, however, asymmetrical because the pairing of integers to form octaves, such as 4 and 8 or 6 and 12, and perfect fifths, such as 8 and 12 or 4 and 6, follows the directions of the sides of the tetractys, whereas the pairing of integers to form perfect fourths, such as 3 and 4 or 9 and 12, is diagonally across the natural geometry of the array of integers in the tetractys. Moreover, the creation of tone ratios is incomplete in the context of Pythagorean mathematics because the number 4 is missing as a generative factor from Plato’s Lambda. By considering the Lambda tetractys with 13 = 1, 23 = 8 and 33 = 27 at its corners as but one face of a tetrahedron with 43 = 64 at its fourth corner, it was found6 that a complete symmetry appeared in the pairing of integers forming the fourth face of the tetrahedron (Fig. 5). All successive octaves lie on red lines, all perfect fourths lie on green lines and all perfect fifths lie on blue lines, these sets of lines being parallel to the three sides of the tetractys forming the fourth face of the tetrahedron. (In
10
the first face, only octaves and perfect fifths are linked parallel to these sides). Its hexagonal symmetry means that, when this fourth tetractys is extended to create other octaves, every number becomes surrounded by six others that are octaves, perfect fourths or perfect fifths. All the numbers in this infinite, planar array may be divided by any one of them to generate the same hexagonal lattice of tone ratios of the Pythagorean scale. It is, of course, not invariant with respect to division by any integer, because not all integers are present in the lattice. For example, all prime numbers are
11
absent. However, ratios of any pair of numbers are unchanged by division of each by the same number. Division of all the numbers in the lattice by any number — whether or not it belongs to the lattice — therefore leaves the tone ratios formed from the pairs unchanged. It does not matter which number in the lattice is picked as the tonic, or fundamental frequency, as the tone ratios created by dividing it by the numbers around it are the same as those formed by the numbers surrounding the number 1. Where one picks one’s tonal ‘origin’ is arbitrary. This simply reflects the way in which the intervals between notes in one octave are preserved in a different octave because every tone ratio is changed by the same factor.
Figure 6 shows the lattice of tone ratios, starting with the tonic, 1. Overtones are shown in yellow circles. Red lines connect octaves (×2), green lines connect perfect fourths (×4/3) and blue lines connect perfect fifths (×3/2). The Pythagorean tone interval 9/8 is
12
13
also indicated by the orange line joining the tonic at the centre of the tetractys (coloured grey) to one corner of it. The tone ratio 27/16 of the major sixth and the tone ratio 243/128 of the major seventh are similarly defined by, respectively, indigo and violet diagonals extending from the number 1 to corners of larger triangles. Successive notes of the musical scale are joined by dashed lines. They zigzag between the octave, the major seventh and the perfect fourth, i.e., between the extremities of each octave and its midpoint.
The perfect fourth of the nth octave has a tone ratio of 2n-1(4/3) = 2n(2/3) and the perfect fifth has a tone ratio of 2n-1(3/2) = 2n(3/4). The corresponding undertones of the nth octave have tone ratios of, respectively, 2-n(4/3) and 2-n(3/2). As 2n(2/3) is the reciprocal of 2-n(3/2) and 2n(3/4) is the reciprocal of 2-n(4/3), the tone ratio of the perfect fourth for a given octave of undertones is the reciprocal of the tone ratio of the perfect fifth of the corresponding octave of tones, and vice versa. This is illustrated in Figure 7 for five octaves of tones and their undertones. Red arrows link octaves, green arrows link the perfect fourths of undertones to the perfect fifths of tones and blue arrows link the perfect fifths of undertones to the perfect fourths of tones. Only octaves, perfect fourths and fifths share this property of reciprocity.
As frequency and wavelength are inversely related, the wavelength of an undertone that is a perfect fourth is the same as the tone ratio of the perfect fifth of the same octave of tones. Table 4 displays the wavelengths of the undertones for eleven octaves. The last column lists the number of their sub-harmonics as a running total. We see that only octaves and perfect fourths have wavelengths that are whole numbers. More important is the fact that the latter are the very integers that appear in the Titius-Bode Law measuring the distances of the planets from Mercury. This is the third clue to its physical basis.
Table 5 shows the zigzag pattern of the Pythagorean musical undertones and their wavelengths. The second column numbers the integer values of the perfect fourths in the purple cells up to 192. The reason for stopping at this number for the eighth octave will be given in Section 8.
5. Theories of the Solar System
The oldest theory of the Solar System is the nebula theory. Originally proposed in the middle of the eighteenth century by Immanuel Kant (1724–1804), the great German philosopher, and developed in 1796 by the French astronomer, Pierre Laplace (1749–1827), it starts with a cloud of interstellar gas and/or dust that was triggered to collapse under its own gravity by some disturbance (perhaps the shockwave from a nearby supernova). The centre of the cloud became compressed as it collapsed and heated up until it formed into a protostar. Viscous drag between the rotating protostar and the gas flowing around it made the latter start to rotate. Some material fell into the protostar and the rest condensed into an ‘accretion disk,’ which rotated around the star and cooled off enough for metal, rock and ice to condense into tiny particles. The metals condensed almost as soon as the accretion disk formed (4.55 to 4.56 billion years ago according to measurements of certain meteors). The rock condensed later (between 4.4 and 4.55 billion years ago). Particles collided and aggregated into larger particles until they became the size of small asteroids. Then gravity took over and pulled in more, smaller particles. They grew to a size that depends on their distance from the star and the density and composition of the protoplanetary nebula. The accretion of these ‘planetesimals’ is supposed to have taken a few hundred thousand to about twenty million years, the outermost taking the longest to form because of the lower density of
14
material near the rim of the disk. About one million years after the nebula cooled, the star’s nuclear reactions expelled its outer layers, this so-called ‘T Tauri Wind’ sweeping away all the gas left in the protoplanetary nebula. Gas giants like Jupiter and Saturn formed because they were massive enough to hold on a relatively large quantity of nebula gas, which was swept away from the smaller planets. The planetesimals slowly collided with one another and became more massive, moon-sized bodies that continued to collide until the planets formed about ten to a hundred million years later.
There were two main problems with the original version of this theory. First, as angular momentum is conserved, the condensation process should have left the Sun with 99% of the Solar System mass with most of the angular momentum, whereas 99% of it resides in the planets’ orbital and rotational motions. The central mass could not have transferred this much momentum to the planets. Second, a hot gaseous ring of the type postulated by Laplace would disperse into space and would not pull itself together gravitationally to form a planet.
A variation of the theory suggested that the protoplanetary nebula was a system of rings that were radiated away from the Sun, somewhat like a series of smoke rings puffed out by someone smoking a cigarette. Apart from the problem whence this chain of rings came, it would require much more time than the estimated five billion years the Sun has existed.
Problems with the nebula theory made people think of an alternative. The French naturalist George Buffon (1707–1788) proposed in 1745 that material ripped off from the Sun by collision with a comet had condensed into the planets. This encounter theory was developed by the American geologist Thomas Chamberlin (1843–1928) and the American astronomer Forest Moulton (1872–1852), who suggested that giant eruptions were pulled off the Sun by the gravitational attraction of a passing star. Later, another geologist-astronomer pair in England, Sir Harold Jeffreys (1891–1989) and Sir James Jeans (1877–1946), theorized that a cigar-shaped gaseous filament was pulled from the Sun by the sideswiping action of a passing star. The middle section condensed into the Jovian planets, and the ends condensed into the smaller planets. This theory accounts for all the planets orbiting in the same direction and in the sense of the Sun's rotation, as well as for the planets' nearly circular and coplanar orbits. In either version, however, this theory has serious failings in that solar matter, whether pulled or ejected, could not have acquired sufficient angular momentum nor could hot gas have condensed into planets. Besides, the probability of a near encounter in our region of the Galaxy is vanishingly small, less than one in many millions. Finally, encounter theories cannot explain why the Earth and other planets display so many elements not found in the Sun.
Improvements to the nebula hypothesis were made in the mid twentieth century. A fragment was imagined to first separate from an interstellar cloud of gas and dust. This was followed by the separation of other fragments. The central region of the cloud was denser than its outer parts and collapsed more quickly. As the rotating cloud broke up, rotation was transferred to each fragment, the motion speeding up as the solar nebula contracted in order to conserve angular momentum. The solar nebula grew by accretion as material continued to fall inward from its surroundings. Large-scale turbulence from gravitational instabilities ruptured the thin accretion disk into eddies, each containing many small particles. These particles gradually built up into larger bodies by some combination of adhesive forces. Repeated encounters among them resulted in the accretion of literally billions of still larger asteroid-sized aggregates (planetesimals), which orbited the centre of the solar nebula. Mutual gravitational attraction led to further encounters and gradual coalescence into many roughly Moon-size bodies, or proto
15
planets, which in turn coalesced to form the planets.
The Asteroid Belt likely represents not the remains of a planet that broke up owing to catastrophic collision with some invading object but one that failed to form because the mass of all the bodies there (less than a quarter of the mass of the Earth’s Moon) was insufficient to create massive enough planetesimals to draw them together by the force of gravity. If it had been the former, one would have expected its orbit to have been perturbed enough to cause some deviation from the Titius-Bode Law, with which the Asteroid Belt agrees well. Alternatively (and more likely), the formation of large bodies could have been disrupted by the powerful gravitational pull of neighbouring Jupiter, which would have tugged them completely out of the belt if they occupied so-called ‘resonant orbits’ that periodically brought them close to the giant planet.
In January 2002 a strange object called a ‘brown dwarf’ was reported7 orbiting a star nearly as closely as Saturn is to the Sun. Brown dwarfs are large balls of gas, much heavier than Jupiter but not massive enough to generate the thermo-nuclear fusion that powers a star. The nearest, confirmed brown dwarf is about 16 light-years3 from Earth (the nearest star, Proxima Centauri, is 4.2 light-years away), although an as yet unconfirmed brown dwarf has been found8 about 13 light-years away. Between 55 and 78 times as heavy as Jupiter, its planetary-scale distance of 14 AU from the star is uncomfortably too close for its size to be explainable by the nebula theory of planetary systems. The problem raised by this object is similar to that raised by many of the massive, extra-solar planets that have been discovered orbiting stars. They are much closer to these
stars than current ideas of planetary formation allow and generally have large orbital eccentricities, raising the question whether the Solar System and its formation is actually atypical of planetary systems. The most likely situation is that there is no unique process by which planetary systems form. That said, in 1992 the Hubble Space Telescope obtained the first images of proto-planetary disks in the Orion Nebula.9 10 Dr. C. Robert O’Dell, a Rice University astronomer, surveyed with the Hubble Space Telescope 110 stars in the Orion Nebula 1500 light-years away and found disks around 56 of them (Fig. 8). At the centre of each disk was a young star. The images showed that the objects were pancake-shaped disks of dust. Some of these disks are
____________________________
3 A light-year is the distance travelled by light in one year. It is about 5.88 trillion miles (9.7 trillion km).
16
visible as silhouettes against a background of hot, bright interstellar gas, while others are seen to shine brightly. Hubble’s images provide direct evidence that dust surrounding a newborn star has too much spin to be drawn into the collapsing star. Instead, the material spreads out into a broad, flattened disk through a combination of centrifugal force and gravitational attraction between objects on either side of the central plane of rotation. The disks are roughly on the same scale as the Solar System and lend strong support to the nebular theory of its origin.
6. Planetary orbitals as musical perfect fourths
The problem of the nebula theory vis-à-vis the Titius-Bode Law is that the condition for stabilising a future planetary orbit, namely the balancing of the centrifugal force acting on the orbiting, would-be planet with the Sun’s gravitational force, merely creates the relationship between its period and average distance described by Kepler’s Third Law. Another dynamical condition that gravity does not seem able to provide is required to determine the relative sizes of the planetary orbits. The fact that physics could not supply one made some astronomers question whether the
numerical relationship discovered by Titius was anything other than coincidence. The fact, however, that both the four largest moons of Jupiter and some extra-solar planetary systems exhibit spacing rules in their orbitals, albeit not of the Titius-Bode kind, discredits this viewpoint because these rules, too, would then have to be due to coincidence, which is
17
implausible. If, as the nebula theory asserts, some disturbance, such as the shockwave from an exploding star, pushed out a clump of gas and dust in the rotating accretion disk to a point where the centrifugal force exceeded the inward gravitational pull of the proto-sun at the centre of the disk, this would have created a tear in it. In fact, many tears would be created as the radiation and gas blast from the exploding star accelerated different clumps of matter as it passed through the disk. Travelling faster than material nearby that had been shielded by the blast, the ejected matter would collide more often with objects in its path and build up its mass owing to the greater likelihood of their greater speed causing cohesion with them. It would literally dig a path through the gas and dust, the trail being made up of bodies that were larger than most of the material in
the accretion disk undisturbed by the exploding star. As the disk rotated, the trail of larger, faster objects moving with it as a whole would curve round and eventually become elliptical, their centrifugal force overcoming the inward gravitational pull by the proto-sun for a while until they had slowed down enough through collisions and had become sufficiently massive for the latter force to counterbalance the former. When this happened, the various trails of aggregated bodies formed rings of material that, being of higher density, attracted matter in the accretion disk, thus widening the gaps between the rings.
A point on a logarithmic curve has polar coordinates (r, θ) related by:
r(θ) = aebθ (a and b are positive constants). Hence, after n further, complete revolutions:
r(θ+2πn) if b = ln2/2π ≈ 0.1103. Therefore:
This particular logarithmic curve crosses any straight line passing through the point r = 0 around which it spirals at points r(2πn) = 2na = a, 2a, 4a, 8a, etc. The distance between
18
successive crossings is twice the previous one (Fig. 10). The same is true for the length of the curve up to these points, as now shown. The differential length ds is given by
The length of the logarithmic spiral up the point with polar coordinates (r, θ) is
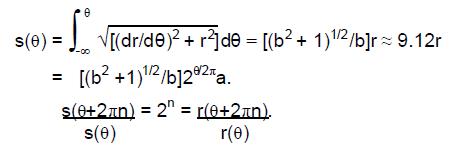
(16)
(17)
(18)
Every revolution of the spiral increases its length by a factor of 2, just as the distance between successive crossings of any straight line through its centre does. As r(2πn) = 2na and s(2πn) ≈ 9.12a×2n, the length of the curve from its centre up to any point on it is just over nine times the distance of the point from the centre. As r(πn) = (√2)na and s(π(n+1))/s(nπ) = (√2), successive revolutions by 180° increases both the radius and the length of the spiral by √2 ≈1.414, showing the meaning of this smallest surd as the factor by which this logarithmic spiral expands in every half-revolution.
It is important to point out here that n can take negative values because the curve winds endlessly in smaller and smaller spirals around its asymptotic centre θ= –∞. The part of the curve that n defines is arbitrary because the logarithmic spiral is self-similar — every corresponding section whose ends are defined by the same pair of angles modulo 2πn is similarly shaped, differing only in scale. n = –∞ denotes the asymptotic centre.
Self-similar spirals are ubiquitous in nature as the form taken by living things that do not change in shape as they grow in size. Let us suppose that the inswirling material of the solar nebula that gave birth to the Solar System followed the inward path of a logarithmic spiral.
This contraction was the opposite to the kind of expansive, spiral development that occurs, for example, in seashells and vertebrate embryos. The spiral motion of the material continued in the accretion disk. It aggregated into spiral bands of
19
denser material that eventually turned into stable, elliptical annuli of bodies in orbit around the young Sun. Assuming that the decrease in density of accretion material with distance was uniform, the average distance of each ring was set by the arithmetic mean of the radii of successive spirals, each half-revolution of which caused that section of the spiral inflow of material to break off and to go into its own orbit, its parameters set by Kepler’s Third Law. Material belonging to the most tightly wind spirals was closest to the Sun and therefore collapsed into it. As the Sun was forming at the same time, sucking dust and gas into it, there is no reason why it should have been at the asymptotic centre of the spiral, which was not an orbital path generated by its gravitational pull on the material of the accretion disk.* The distance from the asymptotic centre of the nth crossing point of the spiral with the major axes of the elliptical orbits is 2na. This centre is distance R from the common centre of the ellipses. The distance Rn of the nth crossing point from the centre of the orbits is
Rn = R + 2na
The mean distance of the nth ring from the centre (Fig. 11) is
dn = ½(Rn + Rn+1) = R + ½a(2n + 2n+1) = R + 3a×2n-1. The distance between the nth and (n+1)th planet after Mercury is
dn+1 – dn = 3a, 6a, 12a, 24a, etc. As the first planet, Mercury was formed from material of the accretion disk within the distance 0≤r≤R1, the average value of which = (0+R1)/2 = ½R1. Its distance from the Sun is dM = ½R1 = ½(R + 2a). According to Equation 20, the distance of Venus from the Sun is
d1 = ½(R1 + R2) = R + 3a.
The distance of Venus from Mercury is
d1 – dM = ½(R + 4a).
According to Equation 22, the distance between consecutive planets is an even or odd multiple of a. If one supposes that this also true of the distance between Mercury and Venus, then
d1 – dM = 2Na or (2N–1)a,
where N = 1, 2, 3, etc. Hence,
½(R + 4a) = 2Na or (2N–1)a.
R = 4(N–1)a = 4a, 8a, 12a, etc,
or
R = (4N–6)a = 2a, 6a, 10a, etc.
R = 2a is excluded because it implies dM = 2a as well, i.e., that Mercury is at the asymptotic centre of the logarithmic spiral, which would not allow its own annulus (and hence itself) to develop. The minimum value of R is 4a. Substituting in Equation 20,
dn = 4a + 3a×2n-1.
d2 = 4a + 6a = 10a,
and
dn/d2 = 0.4 + 0.3×2n-1.
____________________________
* Sir Isaac Newton proved that a logarithmic spiral is the orbit produced by a force that varies as 1/r3.
20
This is the Titius-Bode Law (Equation 1) expressed in terms of the astronomical unit d2, the mean distance of the second ring from the centre of the ellipses. It expresses the average distance from the centre of the elliptical orbits of successive edges of the spiral segments of the accretion disk that eventually form a planet. R = 4a is not, as astronomers have thought, the distance of Mercury from the Sun. Instead, it is the distance of the asymptotic centre of the logarithmic spiral, which, as we shall see, turns out to be close to Mercury. n = 1 corresponds to Venus, n = 2 corresponds to Earth, etc.
As R = 4a, Equation 19 becomes
Rn = 4a + 2na = (4 + 2n)d2/10,
R-∞= 0.4d2 = 4a = R. Why n was wrongly thought to have the singular value of -∞ in the case of Mercury now becomes clear. It signifies the asymptotic point on the X-axis to which the logarithmic spiral converges after winding infinitely many times around it.According to Equation 19, R1 = 3R/2, R2 = 2R, R3 = 3R, R4 = 5R, etc. Therefore,
dn = [1 + (2n-2 + 2n-1)/2]R. Therefore,
dn/R = 1 + (2n-2 + 2n-1)/2 Following the convention that the tonic of the first octave has a tone ratio of 1, the second term on the right-hand side of Equation 32 is the perfect fifth of the (n–1)th octave. The relative distance (dn–R)/R of the nth planet from Mercury is simply the proportion by which the frequency of the perfect fifth of the (n–1)th octave exceeds that of the tonic of the first octave. Alternatively, Figure 7 shows that, as the tone ratios of perfect fifths are reciprocals of those of perfect fourths of their counterpart undertones
21
and as wavelength and frequency are inversely proportional to each other, the planets’ distances from Mercury increase as the wavelengths of successive octaves of perfect fourths of the musical undertones. This reflects the fact that, whereas the tone ratios of perfect fourths are the harmonic mean of those of the tonic and octave, their wavelengths are the arithmetic means of these notes.
dM = ½R1 = 3R/4 =0.3d2. This, and not R = 0.4d2, would be the predicted distance of Mercury from the Sun if the centre of its orbit coincided with those of the other planets, all of whom (apart from Pluto) have almost zero eccentricities (see Table 3). However, the eccentricity of Mercury’s orbit is e = 0.2056, which means that, unlike other planets to a very good approximation, the Sun is not at the geometrical centre of its orbit. If dM is its mean distance from the Sun, its distance at perihelion is dM(1–e) ≈ 0.7944dM. This must be the average distance from the Sun of the material that formed Mercury. Hence, 0.7944dM ≈ 0.3d2, so that dM/d2 ≈ 0.3776. This predicted distance compares well with the actual value of 0.3871 — certainly better than the value of 0.4 appearing in the Titius-Bode Law (the discrepancy is –0.095 compared with +0.1129).
7. Octet patterns in nature
When chemists in the 1860s began to group the known elements according to similar chemical and physical properties, they found that the latter repeated in cycles. Arranged in a periodic table, elements with similar properties occurred in the same vertical column. The chemists discovered eight main groups, or types, of elements (Table 6). Physicists eventually found the reason for this eightfold pattern. The chemical properties of elements are due to the electrons that their atoms either give up or share when they bind to other atoms — their so-called ‘valence electrons.’ Electrons occupy a discrete number of orbitals in a set of quantum shells. Usually the valence electrons in the outermost shell participate in the bonding together of atoms. As this shell possesses eight electrons when filled (Fig. 12), atoms strive to attain this most stable electronic configuration by combining with those elements whose atoms have sufficient number of valence electrons to fill up the shell. Elements at the extreme right column of the table (group VIII), known as the inert, or noble, gases like neon and argon, have atoms with full, outermost shells of eight electrons. They find difficulty in chemically reacting with other elements. When the outer shell is full, a new row, or ‘period,’ of elements begins again with one electron in its outer shell (Group I). These give up an electron in chemical reactions. Group II elements give up two electrons, and so on. Elements whose atoms give up or share the same number of electrons will occupy the same group. As it is this number that determines how they bond to other atoms, elements within the same group display similar chemical properties. Atoms therefore have up to eight stages in the filling of their valence shell.
Particle physicists found in the 1960s that strongly interacting subatomic particles called ‘baryons’ and ‘mesons’ could be classified according to what became known as the ‘eight-fold way.’ This highly successful classification scheme placed these particles in groups of eight, or ‘octets’ (Fig. 13). The Quark Model proposed by Gell-Mann and Zweig in 1964 explained these patterns by postulating the existence of a more fundamental particle called the ‘quark.’ Three types of these particles combined
22
as quark-antiquark pairs or as groups of three quarks to form just those baryons and mesons that had been discovered in the high-energy physics laboratory, as well as one — the omega minus — which was discovered soon after the model was proposed.
Particle physicists describe the forces operating between subatomic particles in terms of so-called gauge symmetry groups. Many believe that the basic constituents of matter are extended objects called ‘superstrings.’ The gauge symmetry group describing the unified superstring force
is the rank-8 exceptional group E8. It was shown in Article 1511
23
that a continuous, mathematical link exists between this group and the algebra of octonions, which is the most general class of division algebra. Article 1612 showed a remarkable analogy between the multiplicative properties of this 8-dimensional algebra (Table 12) and the seven musical octave species known to the ancient Egyptians and Greeks. This correspondence is too detailed and exact to be due to chance. It suggests that the much-sought ‘M-theory’ that encompasses the five superstring theories with supergravity will incorporate the Pythagorean mathematics of the musical scale.
These examples of eight-fold patterns at work in Nature determining the chemical properties of atoms and the interactions of superstrings arise because the cyclic process that renews and exhausts all possibilities — either physical (electron shells, barons and mesons) or mathematical (eight octonions, eight-dimensional E8) — requires eight steps. The space-time predicted by superstring theory has eight dimensions perpendicular to any given direction that superstrings may move along. These comprise two large-scale dimensions of the space that is familiar to us and six dimensions of a hidden, curled-up space. This 2:6 division corresponds in music to the beginning (tonic) and end (octave) of the eight-note diatonic scale and the six notes spread between them. In the atom it corresponds to the two electrons occupying the S orbital and the six electrons in the three P orbitals of the valence shell that together determine the chemistry of elements other than the rare earths.
In view of these examples, it should not come as a surprise that an eight-fold pattern exists in the planets of the Solar System. In fact, it was encountered in Section 1, where Table 1 shows that the Titius-Bode Law is obeyed by the first eight planets (including the Asteroid Belt, which is the remnant of a planet that failed to form) but breaks down for the next two planets. As next explained, this is because, like musical tones repeated on higher octaves, Neptune and Pluto belong to another octet governed by the same principle forming the planets up to Uranus. They obey a re-scaled version of the Titius- Bode Law appropriate to this new octet, Uranus acting as the tonic of a new octave.
8. The octet structure of the Solar System
Logarithmic spiral geometry for the spiralling of matter in the solar accretion disk before it aggregated into planets was shown in Section 6 to result in planetary average distances that obey the Titius-Bode Law. Average distances from the centre of the spiral are simply the wavelengths of the perfect fourths of the undertones of the Pythagorean musical scale:
dn – 4a = (3a/2)×2n 3a/2 is the wavelength of the perfect fourth of the first octave of undertones whose tonic has the wavelength a. Venus (n = 1) corresponds therefore to the perfect fourth of the second octave. In general, the (n+1)th planet from the Sun (the nth planet from Mercury) corresponds to the perfect fourth of the (n+1)th octave. Uranus, the eighth planet from Mercury,* has a distance from it equal to the wavelength of the perfect fourth of the eighth octave, namely, (3a/2)×27 = 192a. Let us suppose that, just as the eighth note of the Pythagorean musical scale is both the last note of one octave and the tonic of the next higher octave, so Uranus both ends the first octet of planets and commences the next one. Then, just as Mercury itself does not obey the Titius-Bode Law in the same way as other planets do because it is not a term in the geometrical progression and is therefore undetermined by it, so Uranus does not obey the law of geometric progression that corresponds to the new octet. According to this view,
____________________________
* As always, the Asteroid Belt is counted as a planet because it is the remnant of one that failed to form.
24
Neptune, the first member (n' = 1) of this octet after Uranus, corresponds to Venus, the first planet (n = 1) after Mercury in the first octet of planets (Table 13).
Octave
Planet
centre = (3/2)×2na1
Mercury 2
Venus 3
Earth 4
Mars 5
(Asteroids) 6
Jupiter 7
Saturn 8
Uranus 9
Neptune 10
Pluto But now, instead of the distance (3a/2)×2n = 3a×2n-1 of the nth planet from the first asymptotic centre, the distance of the n'th planet beyond Uranus will be given by 96a×2n'-1. The reason for this is as follows: The distance from the Sun of the n'th crossing point of the logarithmic spiral in the second octet is
Rn' = R' + 2n'a', where R' is the distance of the new centre and a' is the distance of the first crossing point from the centre. The rescaled spiral becomes centred on the orbit of Uranus, whose distance from the first centre is 192a (Fig. 14). Therefore, R' = 4a + 192a = 196a.
25
The distance from the Sun of the n'th planet beyond Uranus in the second octet is
= 196a + 3a'×2n'-1. This compares with
for planets in the first octet. The orbit of Venus is determined by the second and third crossing points of the spiral at distances from its centre of, respectively, 2a and 4a, the first crossing point being at a distance of a. The latter plays the role of the wavelength of tonic of the first octave of undertones.
Planet Mercury Venus Earth Mars Asteroids Jupiter Saturn Uranus Neptune Pluto The distance 3a of Venus from the spiral’s centre is the perfect fourth of the second octave. Uranus, the first member of the second octet, corresponds to Mercury, which is the first member of the first octet, and Neptune (n' = 1), the second member of the second octet, corresponds to Venus (n = 1), the second member of the first octet. The distance between the two spirals associated with Uranus is 28a – 27a = 128a, the outer one being 64a units from the planet’s orbit. The inner spiral for Venus corresponds to the inner spiral for Neptune, which is at the same position as the outer spiral for Uranus. Venus’s inner spiral is distance 2a from the asymptotic centre. Hence, as the spiral for the second octet is a logarithmic spiral as well,* Neptune’s inner spiral is distance 2a' from its centre, which is at the crossing point of Uranus’s orbit. Therefore, 2a' = 64a, a' = 32a and Equation 36 becomes
dn' = 196a + 96a×2n'-1 As 7 + n' = n, the distance of the (n+1)th planet from the Sun is
____________________________
* As a' = 25a, i.e., larger than a by an integer power of 2, the spirals for the two octets are identical.
26
Dividing by 10a (d2) to convert dn into Astronomical Units, the Titius-Bode Law for the second octet of planets is
dn = 19.6 + 0.3×2n-3. For Neptune (n = 8), d8 = 29.2 AU, comparing well with the actual value of 30.06 AU. For Pluto (n = 9), d9 = 38.8 AU, also agreeing well with the actual value of 39.48 AU.
By making just one reasonable assumption that the planets have the same octet pattern as that found in music, the quark make-up of baryons and mesons and the group mathematics of superstrings, it has been shown that, far from being anomalous, Neptune and Pluto actually fit the same musical pattern of perfect fourths underlying the Titius-Bode Law as the other planets do (Table 14). The discrepancies are 2.9% under for Neptune, comparing with the old value of 29.0% over, and 1.7% under for Pluto, comparing with the huge discrepancy of 95% over that caused doubt among some astronomers that Pluto is a true planet. Mercury plays the role of the tonic of the musical scale and Uranus its octave, which is the tonic of the next higher octave of notes. The unit octonions comprise the real number 1 and seven imaginary octonions. The two planets correspond to the real unit octonion. The meson octets each comprises a so-called ‘isospin singlet state’ as well as seven other quark-antiquark bound states (e.g., the η meson in the spin-0 octet shown in Fig. 13). This 1:7 differentiation corresponds to the distinction between Mercury and the seven other members of the Solar System up to Uranus forming the first octet.
The predicted distance of the next hypothetical planet beyond Pluto is d10 = 19.6 + 0.3×27 = 58.0 AU, not 77.2 AU, as predicted by the unmodified Titius-Bode Law. This value agrees precisely with the current distance of a large Kuiper Belt Object called 2004 XR 190 (nicknamed “Buffy”) whose discovery13 by astronomer Lynne Allen with the Canada France Hawai Telescope during the operation of the Canada-France Ecliptic Plane Survey was announced on December 15, 2005. The large inclination of 47° of its orbit to the ecliptic makes astronomers think it is a Kuiper Belt object, some of which have large inclinations. However, Pluto’s orbit has an inclination of over 17° and so, if Pluto is a real planet (some astronomers do not think it is, an issue discussed in Section 10), the even larger inclination of Buffy is no reason to discount it as a true planet because it could have arisen from a cause similar to what made Pluto’s inclination large. Furthermore, unlike observed Kuiper Belt objects, it has an almost circular orbit, which is consistent with its being a real planet, although complex gravitational interactions in the early history of the solar system may also account for this. The additional fact that the measured distance agrees exactly with prediction makes one optimistic that it is not just coincidental, although caution is necessary in deciding whether this does, indeed, amount to a spectacular confirmation of the explanation of the Titius-Bode Law given in this article.
Beauty is a quality of eternal truth and mathematical beauty shines brightly in the Pythagorean character of the Solar System, as will be evident shortly. Another criterion is the set of ten Hebrew Divine Names assigned in Kabbalah to the ten Sephiroth of the Tree of Life, for a large body of evidence both reported by the author14 and as yet unpublished15 has shown that they mathematically prescribe the archetypal nature of Pythagorean whole systems through their gematria values.* Examples of this prescription will be discussed next.
____________________________
* By assigning integers to the letters of the Hebrew alphabet, a Hebrew word can be converted into a number that is the sum of its letter values. This was the basis of the ancient practice of gematria.
27
Table 1 indicates that the ratio of the average distance from the Sun of Uranus, the last member of the first octet, and that of the asymptotic centre of the logarithmic spiral is predicted to be 19.6/0.4 = 49 (actual value ≈49.205). This number is highly significant because it is the number value of the Divine Name El Chai (“God Almighty”) assigned to Yesod, the ninth Sephirah. Here is a remarkable illustration of how a Godname prescribes aspects of a divine archetype, for the Solar System is an arena for evolution (at least on the third planet from the Sun), and its structure has therefore to conform to the nature of God, Who has ten aspects or qualities embodied by the Sephiroth. This is not to suggest, of course, that God created the Solar System in the biblical sense. Instead, it is to assert that any holistic system — whether a superstring, living cell or human being must conform to the pattern of the Tree of Life. Just as the Pythagorean, musical octave is whole and complete, so the first eight planets up to Uranus form a whole that — because it is a whole — must be prescribed by the Divine Names. El Chai also determines the crossing point of the inner spiral of Uranus with distance 128a from the centre because, as the wavelength of the seventh octave of undertones (Table 5), 128 is the 49th note above the tonic 1 of the first octave. It is also the 50th note, showing how the Godname Elohim assigned to the third Sephirah, Binah, with number value 50 prescribes the octet of planets.
The number 192, the wavelength of the perfect fourth of the eighth octave, is the 15th whole integer in Table 5. 15 is the number value of Yah, one of the two Divine Names assigned to Chokmah, the second Sephirah, which therefore prescribes the distance of Uranus from the asymptotic centre. Yah prescribes the distance 4a of the latter from the Sun because 4 is the wavelength of the 15th undertone. According to Equation 30, the distance from the Sun of the outer spiral associated with Uranus is R8 = 4a + 256a = 260a = 26×10a. Table 5 indicates that 256, the distance of the outer spiral of this planet from the centre, is the wavelength of the 15th subharmonic, showing how Yah prescribes the size of the octet of planets. The mean Earth-Sun distance is 10a (see Equation 28). Therefore, this point on the outer spiral is exactly 26 AU from the Sun. This shows how the Divine Name Yahweh with number value 26 prescribes the section of the logarithmic spiral that generates the full octet of planets.
It is of profound, religious significance that the most commonly known ancient Hebrew Godname measures through its number value the size of the part of the accretion disk that forms the octet of planets in terms of the Earth’s average distance from the Sun! R7 = 132a and R8 = 260a, so the average distance of Uranus from the Sun = d7/d2 = ½(R7 + R8)/d2 = ½(132a + 260a)/10a = ½(13.2 + 26) = 19.6 AU, comparing well with the actual value of 19.19 AU. This shows explicitly how the number value 26 of Yahweh determines the distance of Uranus. The Pythagorean Tetrad (4) determines this distance because the distance (in terms of a) of the outer spiral for Uranus from the asymptotic centre = 28 = 256 = 44, a beautiful, mathematical property of the octet of planets. The distance
28
between Mercury (distance 0.3d2 = 3a from the Sun) and Uranus (distance 196a from the Sun) is 193a. 193 is the 44th prime number! Once again, the Tetrad appears in this numerical prescription of the distance between the first and last planets of the first octet. This will be commented upon shortly.
That the octet of planets does, indeed, constitutes a whole or a Tree of Life pattern is indicated by the fact that the inner form of the Tree of Life — the seven enfolded, regular polygons shown in Figure 15 — is shaped by 47 tetractyses with 260 yods outside their shared edge, that is, the yods in 26 separate tetractyses (47 is the 15th prime number and is thus prescribed by the Godname Yah, whose number value is 15). In the planetary manifestation of this blueprint, each yod corresponds to the distance a and a tetractys corresponds to 10a — the mean Earth-Sun distance.
The Godname Eloha assigned to Geburah, the sixth Sephirah, with number value 36 prescribes the distance a' = 32a of the first crossing point of the second spiral from its asymptotic centre because, according to Table 5, 32 is the wavelength of the 36th note, counting from the tonic 1.
The distance of the n'th planet from the asymptotic centre of the second logarithmic spiral is 96a×2n'-1 = 48a×2n'. Table 4 indicates that 48 is the wavelength of the fortieth undertone, counting from the tonic of the first octave with a wavelength equal to 1. 40 = 4×10 = 4(1+2+3+4) = 4 + 8 + 12 + 16, i.e., this number is the sum of four integers spaced four units, starting with 4. This and the earlier results expressed by the number
29
4 are examples of the Tetrad Principle formulated by the author16 whereby the fourth member of a class of mathematical object or the sum of the first four members of a sequence of mathematical objects is always a parameter of the universe. In this case the Tetrad naturally determines via the musical scale the parameter 48 setting the scale of the logarithmic spiral associated with the second octet of planets. The Titius-Bode Law is, indeed, a universal law, not merely a rule that applies only to one of the many planetary systems in the universe. 48 is also the tone ratio of the fortieth tone, that is, the thirty-ninth note after the tonic of the first octave. There are (39 + 38 = 77) notes and intervals beyond the tonic up to this note. 77 is the 76th integer after 1. This shows how Yahweh Elohim, Godname of Tiphareth, with number value 76 prescribes the distance 48a between successive crossing points of the second logarithmic spiral.
The number 384 measuring the distance of Pluto from the asymptotic centre of the logarithmic spiral is the 16th sub-harmonic (16 = 15th integer after 1), showing how the Divine Name Yah with number value 15 prescribes the distance of the tenth planet from the first planet. Table 4 shows that 384 is the 61st smallest wavelength, starting from 1, the tonic of the first octave. 61 is the 31st odd integer, where 31 is the number value of El (“God”), the Hebrew Godname assigned to Chesed, the fourth Sephirah of the Tree of Life. Table 2 shows that 384 is the 61st tone and the 30th overtone, that is, there are 30 tones with fractional tone ratios up to the tone ratio 384. This has the following remarkable geometrical representation: when the decagon is divided into its triangular sectors and the latter are each converted into the ten dots of a tetractys, 61 dots are created, of which 30 lie on its boundary and 31 are in its interior. All overtones up to 384 can therefore be assigned to dots on the sides of the decagon and all fractional tone ratios between 1 and 384 can be assigned to dots in its interior, with 1, the tonic of the first octave, appropriately at its centre (Fig. 16). The Decad (10) is the perfect number of the Pythagoreans. Measuring the fullness of Divine Unity (the Monad), it is symbolised by the tetractys. As well as measuring the number of planets in the Solar System, it also determines the maximum distance the logarithmic spiral extends to create them.
The Pythagorean Tetrad defines the number 384 in the following way:
384 =
4! 4! 4! 4!
4! 4! 4! 4!
4! 4! 4! 4!
4! 4! 4! 4!This serves as another example of the Tetrad Principle at work. The facts that the first term in the Titius-Bode Law for the first octet of planets is 4 and that planetary distances are determined by the wavelengths of perfect fourths of the musical undertones further illustrate this potent principle.
The average distance of Pluto from the Sun is 388a and the average distance of Mercury from the Sun is 3a. The average distance between the first and tenth planets is 385a, where
385 =
22 32
42 52 62
72 82 92 102.This is a stunningly beautiful property! Is it a curious accident? No. Who can deny that it bears the hallmark of a Designer? In Astronomical Units this distance is 385a/10a = 385/10 = 38.5, that is, the arithmetic mean of the squares of the first ten natural integers. The actual average distance of Pluto from Mercury is 39.09 AU, a discrepancy
30
31
of only 1.5% from the theoretical value of 38.5 AU! These results are very convincing evidence in favour of Pluto being a true planet, not merely an escaped moon of another planet.
Table 13 indicates that R7 = 132a. The theoretical distance between the first planet and the inner spiral of the last planet of the first octet = 132a – 3a = 129a. The number value of Yahweh Sabaoth, Godname of Netzach, which is the seventh Sephirah, is 129, showing how it prescribes this parameter of the first octet of planets.
Figure 17 depicts how successive division of circles into pairs of similar circles reproduces the powers-of-2 scaling of the logarithmic spiral that determines the average distances of the planets from the Sun.
The distance of Venus from the asymptotic centre is 3a, the distance of Earth from Venus is 3a and the distance of Pluto from Earth is 378a. These distances are encoded in the inner form of the Tree of Life (Fig. 18) in the following way: the two sets of the first six polygons are prescribed by the Godname Elohim because its number value 50 is the number of their corners. They are made up of 378 coloured yods other than the three white yods (one corner of the triangle and two corners of the hexagon) that coincide with Chokmah, Chesed and Netzach on the Pillar of Mercy, the three analogous white yods coinciding with Binah, Geburah and Hod on the Pillar of Severity and the two endpoints of the root edge shared by each set of polygons. The three white yods on one side of the central pillar of Equilibrium denote (in units of 1/10 AU) the distance of Earth from Venus and the three white yods on the other side denote the distance of Mercury from Venus.
We saw earlier that the octet of planets Mercury-Uranus constitutes a Tree of Life pattern because the size of the outer spiral of Uranus — 260a — is the number of yods creating the shape of this pattern. The above result indicates that the first six polygons also constitute a Tree of Life pattern. This is confirmed by the following extraordinary correlation between their yod population and planetary distances: associated with each set of six polygons are 25 corners and 168 other yods (Fig. 19). Compare this with the prediction* that the mean distance (in terms of 1/10 AU) of the Asteroid Belt from
____________________________
* This does not take into account the relatively large eccentricity of Mercury’s orbit, which is probably a feature acquired since the formation of the planets.
32
Mercury is 25 (actually 23.8) and the average distance between the Asteroid Belt and Uranus is 168 (actually, 164.2). The 25 corners associated with the six enfolded polygons define the distance from Mercury of the first four planets after it (counting the Asteroid Belt formally as a planet), whilst the remaining yods define the distance between the Asteroids and Uranus — the last member of the octet.
This is truly remarkable, for it has the profound implication that the octet of planets in the Solar System conforms to the Divine blueprint of the Tree of Life! The four (
) yods coinciding with the positions of the Sephiroth in the Tree of Life symbolise the distance 4a between the Venus and Mercury and the 189 other yods symbolise the distance 189a between Venus and Uranus.
That this correlation is not a coincidence is indicated by the remarkable fact that there are 168 yods on the boundaries of both sets of six polygons outside their shared edge (Fig. 20).
The number 168 determines their shape because it is the number value of Cholem Yesodoth (מלח יסודות), the Kabbalistic title of the Mundane Chakra of Malkuth. Its physical significance as the basic structural parameter of superstrings has been discussed in most of the author’s earlier articles.
33
In analogy to the notes of the Pythagorean scale, Mercury represents the tonic, whilst the seven planets beyond Mercury up to Uranus represent the seven notes above the tonic, Uranus completing the planetary octet and musical octave and playing the same role for the next octet containing Neptune and Pluto as Mercury does for the first octet, i.e., its first member or musical tonic.
9. Planetary distances and superstring theory
The symmetries displayed by the forces of nature are expressed by physicists in the language of a branch of mathematics called ‘group theory.’ The mathematical fields that represent the particles mediating a given type of force are said to be the gauge fields of the gauge symmetry group expressing the symmetry of this force. The mathematical transformations belonging to a gauge group are defined by its set of generators. The dimension N of a symmetry group is the number of independent generators defining its transformations. Each generator is associated with its own gauge field. N gauge fields are therefore associated with a symmetry group of dimension N. The complete set of N generators of a group obeys the rules of an abstract algebra called Lie algebra. This gives rise to a certain algebraic equation, solutions of which are specified by a set of N points in an l-dimensional Euclidean space, where l is the rank of the group. Each point defines a root of the group. l of the N roots are said to be zero roots because they denote points at the centre of the diagram representing these roots, and (N–l) roots are called non-zero roots because they denote points a non-zero distance from this centre.
Physicists Gary Schwarz and Michael Green made the important discovery in 1984 that the gauge symmetry group describing the symmetries of the forces other than gravity acting between 10-dimensional superstrings had to have the dimension N = 496 in order that the theory be free of quantum anomalies. They pointed out that two groups: E8×E8 and SO(32)* have this dimension. The former is the one that first became favoured by string theorists. The group E8 is called the exceptional group of rank 8. It has dimension 248 (half of 496). Its 248 roots consist of 8 zero roots and 240 non-zero roots. The 496 roots of E8×E8 thus consist of (8+8=16) zero roots and (240+240=480) non-zero roots. The 8 zero roots of E8 comprise a zero root of one kind (which need not be specified here) and 7 of another kind. Similarly, the 240 non-zero roots of E8 consist of 128 non-zero roots of one kind and 112 of another kind. The root composition of E8×E8 is laid out below:
Let us now compare the root composition of E8 with the distances between the planets. Inspection of Table 13 shows that (in terms of a) the outer spiral of Uranus is at a distance R8 = 260 from the Sun and the outer spiral of Earth is at a distance R 3 = 12. The distance between the outer spirals of the third and eighth planets = R8 – R3 = 260 –
____________________________
* A third group contained in the other two groups has since been found to be free of anomalies.
34
12 = 248 (Fig. 20). Amazingly, this is the dimension of E8! The outer spiral of Mars is at a distance of R4 = 20. The distance between the outer spirals of the fourth and eighth planets = R8 – R4 = 260 – 20 = 240. This is the number of non-zero roots of E8. The distance between the outer spirals of Earth and Mars = R4 – R3 = 20 – 12 = 8. This is the number of zero roots of E8. The Earth occupies a unique position in the Solar System in that the distance between its outer spiral and the edge of the octet is 248 units — the very number of roots of the superstring gauge symmetry group. Its neighbour Mars defines the number of non-zero roots and the distance between them measures the number of zero roots. Moreover, the distance of the inner spiral of Uranus is R7 = 132, so that the distance between its inner and outer spirals = R8 – R7 = 260 – 132 = 128.
As stated earlier, this is the number of non-zero roots of a certain kind. The distance between the outer spiral of Mars and the inner spiral of Uranus = R7 – R4 = 132 – 20 = 112. This is the number of non-zero roots of another kind (see above). The distance 240 between the innermost and outermost spirals of the outer four planets of the octet splits into the pair of integers:
240 = 112 + 128, measuring, respectively, the width of these spirals for the first three planets and the width for the fourth one. Remarkably, this division is the same as those defining the number of the two types of non-zero roots of E8. The pattern of distances for the octet of planets mirrors the root structure of the mathematical symmetry group describing superstrings! Hard though this may seem to believe, it has the following simple but profound reason: as proved in earlier work,17 E8 belongs to the Tree of Life description of the forces of nature. The mathematical explanation of the Titius-Bode Law presented in this article is also part of the Tree of Life blueprint, for it applies to any planetary system. The same pattern of numbers must ipso facto manifest in both the Solar System and the superstring because both are wholes in the Pythagorean sense, conceived according to the Divine blueprint of the Tree of Life. Figure 15 shows the geometrical form of this blueprint and how it embodies the number 260 measuring the
35
size of the octet.*
Once again, these distances are an example of the Tetrad Principle because

The sum of the first three powers of 2 is 112, which is the distance spanned by the Asteroid Belt, Jupiter and Saturn. The fourth power of 2, i.e., 27, is the distance between the two spirals of Uranus. The 3:1 division in the number of powers reflects the same pattern in the last four planets of the octet.
The distance between the inner spiral R4 of the Asteroid Belt and the outer spiral R8 of Uranus is 240, whilst the distance between the Asteroids and Uranus is 168. The remaining distance is 72. These numbers are expressed by the tetractys representation of the number 240:
The sum of the numbers 24 at the corners of the tetractys is 72 and the sum of the numbers at the corners and centre of the hexagon is 168. The central integer 24 is the predicted distance between the Asteroid Belt and Jupiter (the actual distance is 24.3). In terms of superstring theory, 240 is the number of non-zero roots of E8, 72 is the number of non-zero roots of E6, an exceptional subgroup of E8, and 168 is the number of nonzero roots of E8 that do not belong to E6.
Ignoring the fact that the centre of its eccentric orbit is not located at the Sun (as in the case of other planets to a good approximation), the distance of Mercury from the Sun is predicted to be 3 units. The distance of the outer spiral of the eighth planet completing the octet is R8 = 260. The distance between the first planet and the edge of the octet = 260 – 3 = 257. This is the 55th prime number, where
55 =
2 3
4 5 6
7 8 9 10is the tenth triangular number. This demonstrates for the second time how the Pythagorean Decad defines properties of the Solar System. It is evidence that the distance of Mercury from the Sun is correctly given by ½R1 for, had this not been the case, neither this result nor the spectacular property of the distance 385 between Mercury and Pluto being the sum of the squares of the first ten integers would have
____________________________
* It is amusing that the eccentricity of Pluto, the tenth planet, is 0.248, whilst its orbital period is 247.92 years, that is, almost 248. Two orbital parameters of Pluto are approximately the dimension 248 of the superstring symmetry group E8!
36
been true. We encountered earlier a similar property in finding that the distance between Mercury and Uranus is 193, the 44th prime number. The extra distance between Uranus and its outer spiral = 257 – 193 = 64 = 43, which is another beautiful illustration of the Tetrad Principle. The Solar System is measured out with the Pythagorean yardstick of the number 4. No wonder that one of the ancient titles assigned by the early Pythagoreans to this number was “holding the key of nature”!
10. Is Pluto a planet?
Although the International Astronomical Union still declares Pluto to be a planet,18 some astronomers believe that it was not formed at the time of the other planets but is a satellite of Neptune that was knocked out of orbit. The reasons19 they give for this belief are:
-
Inclination of its orbit compared to the ecliptic is 17.148°;
-
Large orbital eccentricity: 0.248 (Earth's eccentricity: 0.0167);
-
Composition: Pluto is composed of:
-
core of hydrated rock (70% of mass);
-
mantle of water ice;
-
atmosphere containing methane ice (and possibly: N2, CO, CO2). This composition is very different from the other outer
planets because they are mainly composed of gas. Therefore, Pluto’s density is larger than the other outer planets.
-
-
Pluto has a high albido: ±0.5. Remarkably, it is irregular; Pluto has the largest global-scale contrast in the solar system. This
indicates that the planet is active; -
Charon (Pluto’s satellite) is extraordinary large compared to Pluto: Pluto’s radius:Charon’s radius = 1:0.5, in comparison with:
Earth’s radius:Moon’s radius = 1:0.3 and Mars’s radius:Phobos’s radius = 1:0.003. This makes some astronomers believe that
Pluto and Charon may be a double planet.
The fact, however, that Pluto’s composition is more like that of the asteroids in the Kuiper’s Belt is hardly unambiguous evidence that it, too, was once an asteroid. The relative tenuity and coldness of the material on the edges of the accretion disk that condensed into the Solar System would lead one to expect any bodies to have formed there later than those nearer the Sun and to display a composition different from that of the gaseous giant planets, especially if the outer rim of the gaseous accretion disk was mixed with material from the Kuiper Belt.. Nor is its large orbital eccentricity evidence that it is not a planet, for Mercury’s eccentricity is almost as large, yet no one disputes that it is a genuine planet. Pluto differs from objects in the Kuiper Belt by having an orbital inclination to the ecliptic of about 17° — much larger than the several degrees of most Kuiper Belt objects. This difference needs to be explained if Pluto is such an object that left the Kuiper Belt some time in the past. There have been a number of models proposed. None has worked. It has been theorized that Pluto was a natural satellite of Neptune and that Triton, now one of its satellites, was originally in a heliocentric orbit. Their orbits were changed by a collision, which also created Charon, Pluto’s satellite, through tidal forces. However, computer simulations of the orbits and dynamics of Neptune and Pluto have made this scenario very unlikely. It also seems improbable that an object far enough away from the Sun to belong to the Kuiper Belt could have been captured by Neptune. Charon could have been a Kuiper Belt object that was captured by Pluto. This would be consistent with its relatively large size, for one object — Quaoar — has been found in the Kuiper Bet with about one-half the size of Pluto, that is, it is about as large as Charon.20 Finally, Mercury has an orbital inclination of about 7°, which is not much smaller than the average of 10±1 degrees21
37
reported by March, 1999 for Kuiper Belt objects. Yet no one would argue that Mercury is such an object! The relatively large inclination of Pluto’s orbit compared with other heliocentric planets is not unambiguous evidence that it is an asteroid, for it is possible that this light body could have been formed from the planetary nebula but have been subsequently knocked into an orbit of a different inclination through one or more collisions with other objects. This is consistent with the relatively large eccentricity of its orbit, which suggests that the orbital plane changed from what it was during the formation of the planets. It is surely not coincidental that the two planets Mercury and Pluto that have relatively large eccentricities also have relatively large orbital inclinations. If one planet can have a large orbital inclination without having to be considered a Kuiper Belt object, why should the same not apply to another planet?
Contrary to what its protagonists believe, the idea that Pluto is not a natural planet has no strong argument or evidence to support it. Even if objects in the Kuiper Belt are found that are as large as Pluto (or even larger), this does not cast doubt on whether it is a planet, for why should there not be such objects in the primordial debris field? But for the fact that Pluto did not seem to obey the Titius-Bode Law at all, arguably there would have been little incentive to doubt that Pluto is a planet. However, as we have seen, Pluto does in fact obey the theory underlying the law to a very good degree of accuracy. This is inexplicable if it had been merely a satellite of Neptune that was struck by Triton and flew away into its current, heliocentric orbit. For the Titus-Bode Law governs those bodies that condensed out of the primordial gas cloud, not objects that later assumed stable orbits around the Sun through collisions with other detritus that never managed to aggregate into planets. Protagonists of the satellite model might be on firmer ground if the theory presented here had restored Neptune to the fold of planets obeying the Titius-Bode law but still excluded Pluto. However, in the theory presented here restoring Neptune automatically reinstates Pluto. Unless the agreement between its predicted distance and its actual distance is a highly implausible coincidence (but, then, what about the beautiful Pythagorean property of the number 385 revealed on page 30?), the fact that accurate predictions can be made for both Neptune and Pluto is strong evidence that the latter is a true planet. The signature of a true planet should be that it obeys the correctly understood form of the Titus-Bode Law, which this article has shown Pluto to do with an acceptable degree of accuracy.
11. Planets beyond Pluto?
It remains an open question as yet whether the Solar System has more than nine true planets (as opposed to Kuiper Belt objects that may be mistaken for them). It is an active research topic amongst astronomers. BBC News reported on 13 October, 1999 work by Dr John Murray22 of the UK’s Open University that suggests a large planet orbits the Sun a thousand times further away than Pluto, that is, thirty thousand times further than Earth. Murray, who studied the motion of so-called ‘long period’ comets, analysed the orbits of thirteen comets in the Oort Cloud, a region of the Solar System about 50,000 AU from the Sun and about one-third the distance to the nearest star containing an estimated 100 billion comets that spend millions of years before being deflected by collisions into an orbit bringing them into the inner Solar System. He detected signs of a single massive object that was disturbing all of them. Although not yet observed, the planet is several times bigger than Jupiter, the largest known planet in the Solar System. At three thousand billion miles from the Sun, it would take almost six million years to orbit it. It would not have been already found because it is too faint and moves too slowly. It has been suggested that the object is a planet that has escaped from another star because it orbits the Sun in the opposite direction to that of the other
38
planets. Professor John Matese of the University of Louisiana at Layfayette came to the same conclusion in a similar study.
It will be difficult to establish that any planetoid or object found* to be orbiting the Sun further from Pluto is a natural planet (that is, one formed at the time of the known planets) and not some Kuiper Belt object that escaped and was forced gradually into a heliocentric orbit. This article predicts that the next planet after Pluto should have a mean distance from the Sun of 58 AU – exactly that measured for the recently reported object called “Buffy,” although it remains to be determined whether this is more than coincidence.
The Kuiper Belt is a disk-shaped region between 30 and 100 AU from the Sun that contains many icy bodies. The predicted average distance from the Sun of the fourth member of the second octet brings its orbit well into the Kuiper Belt, as does Pluto’s orbit. It would be outside the so-called “classical KBO” orbit near about 50 AU, making a small planet difficult to detect among the thousands of objects already observed in the Kuiper Belt. But one such object precisely satisfying the modified Titius- Bode Law has now been detected, although regarded at the moment by astronomers as a Kuiper belt object. Being so far away, it would likely obey the Titius-Bode Law more accurately than Pluto, whose small deviation from the version formulated here is probably due in part to the gravitational pull of its large neighbour Neptune. This, indeed, is the case with Buffy, whose current distance agrees precisely with prediction, although it spends all its time between 52 and 62 AU from the Sun.
12. Satellite evidence
Using satellites of the planets within the Solar System to test the Titius-Bode Law is complicated by the fact that many small satellites are likely captured bodies that did not form directly along with the present planet or may have had their orbits drastically changed during the early evolution of the Solar System. The smaller the satellite in the sample, the more uncertain is its eligibility. In order to test the idea proposed in this article that planets beyond the eighth one belong to a rescaled octet, it is necessary to have a test sample of at least nine satellites for a given planet. This is because the changeover to the new octave described by its own version of the law — the form that needs testing — occurs with the eighth planet and so the ninth one is the first proper instance of the new version. However, it is these more distant satellites whose origin may be uncertain enough to render meaningless any disagreement between prediction and observation. Testing the law is therefore problematic for n = 8–15.
Jupiter is the most obvious planet to analyze because its four Galilean satellites are thought to be natural, being much larger than its other, much lighter, orbiting bodies. Uranus also has four or possibly five satellites that stand out from its other smaller
____________________________
* A planetoid 800-1100 miles in diameter and as far away as 84 billion miles was announced in March 2004. Called "Sedna," it is the largest object seen since Pluto was discovered in 1930.
39
satellites. Both Saturn and Neptune, however, have only one large satellite, making it difficult to test the rule. The smaller planets have few or no satellites, making testing impossible. Therefore, only the Jovian and Uranian systems provide enough information to test distance rules.
Table 15
Satellite
(1,000 km)
(relative)Io Europa Ganymede Callisto Howard L. Cohen pointed out23 in 1996 that the four Galilean moons of Jupiter obey:
Table 15 compares the actual and predicted distances of these satellites. The agreement is good. Almathea, the next Jovian satellite to be discovered after Galileo found those listed in the table, orbits 180,000 Km from Jupiter, or 0.43 of Io’s distance. Cohen pointed out that, if n = -∞ for this satellite, its predicted distance is 0.5, which is another good agreement. However, as in the case of Mercury, this value of n is counterintuitive and should actually refer not to a satellite but to the asymptotic centre of the spiral that would have generated Jupiter and its natural moons. Moreover, Equation 43 is not a proper expression of the general Titius-Bode Law as the values of n should start with 1, not 0. Instead, therefore, let us write for these five satellites the form of the rule:
where n = 1 for Io, i.e., a is the distance of Almathea from Jupiter (for the moment, we use the standard interpretation). Let us work with the actual distances of the five satellites rather than make assumptions about which satellite should provide the unit of distance. Using Almathea and Io to determine a and b, then a = 180 and b = 242. Table 16 compares the actual and predicted distances of the test satellites:
(1,000 Km)
(1,000 Km)Europa Ganymede Callisto We find that, whilst the agreement is good for Europa, it is poor for Ganymede and Callisto. A progression of powers-of-2 requiring values of n that start from the sensible value n = 1 therefore shows good agreement only for one of the five satellites. However, Table 15 shows that the spacings between Io, Europa, Ganymede and Callisto do increase as powers of 2. The predicted spacings between Almathea-Io, Io-Europa, Europa-Ganymede and Ganymede-Callisto are, respectively, 242, 242, 484 & 968, comparing poorly with the measured values of 242, 249, 399 & 815. This means
40
therefore that the satellite Almathea does not fit the historical form of Titius-Bode Law because its use for determining values of a and b leads to a false, poor fit for other satellites.
(1,000 Km)
(1,000 Km)Ganymede Callisto Suppose, instead, that Io and Europa are used to fix a and b. Table 17 compares the actual and predicted distances for the remaining two test satellites. The fit is even poorer. If they conform to a general Titius-Bode Law, the spacings between Io, Europa, Ganymede and Callisto should be in the proportions 1:2:4. Instead, they are in the ratio 1:1.60:3.27, which is a poor match.
Let us check, however, whether the reason for the non-Bode behaviour of the five satellites is that it is wrong to assume that ‘a’ in Equation 41 is the distance of the nearest natural satellite from the planet. The theory presented here indicates that this is the case, for this distance should be 3a/4, not a. The predicted correct form of the law is
This means that 3a = 180 for Almathea and a = 60 for the new law, whereas 4a = 180 and a = 45 for the old law. Table 18 compares the actual and predicted distances for the four Galilean satellites:
For all four satellites, the new form of the law gives a far superior fit than the traditional version. In the case of Io, it is excellent. Astronomers have falsely concluded that the satellites of Jupiter do not fit the Titius-Bode Law, whereas the true reason for this is that they have misunderstood it by believing that its first term represented the distance of the first planet or satellite from, respectively, the Sun or planet, whereas it really denoted their distance from the asymptotic centre of the logarithmic spiral. The difference in the case of the planets amounts to 0.4 – 0.3 = 0.1 AU, which was small enough compared with 0.4 AU not to distort significantly the agreement between the planetary data and the wrong form of the law. However, a similar 25% error in the assumed value of the nearest satellite’s distance underestimates the total distance by 25% because the deduced value of a appears in both terms of Equation 45 and so the discrepancy gets larger, the further the satellite is from the planet, as Table 18 indicates. That said, the measured spacings 249, 399 and 815 between Io, Europa, Ganymede and Callisto still show 10-28% difference from the values 180, 360 and 720 predicted by the new form of the Titius-Bode Law. This is not large enough to be certain that they do not obey even the correctly interpreted law, but it is also not small enough
41
to be sure that they do. The four major satellites are known to be locked into orbital periods that are each twice that of the next inner satellite. It is believed that the reason for this is that tidal drag is forcing them outwards to lock to the period of the
Table 19
(Uranian radii)Miranda Ariel Umbriel Titania Oberon outermost, large satellite, Callisto. This factor distorts the picture and makes a test of any theory of the Titius-Bode Law based upon satellites inconclusive.
The major satellites of Uranus also have non-Bode spacings (Table 19). The spacing between Titania and Oberon is less than that between Umbriel and Titania, despite
42
Oberon being further out from Uranus than Titania is. The lesser satellites of Uranus have mean distances of the order of 2-3 Uranian radii or several hundred radii. Their spacings decrease, then increase, showing no signs of obeying a Titius-Bode rule, whether old or new.
13. Conclusion
As a planetary nebula collapses into an accretion disk centred on a protostar, it aggregates into vortical currents or streams of material flowing along a logarithmic spiral. Logarithmic spirals are ubiquitous in nature as the geometrical shape of biological systems. One such example is the golden spiral found in seashells such as the Nautilus, successive radii of whose curves are in the proportion of the Golden Ratio. The cochlea is another example (Fig. 21), although its spiralling is not confined to a plane. The asymptotic centre of the logarithmic spiral does not coincide with the nucleus of the disk — the future Sun — because the swirling is not a stable state like elliptical orbital motion produced by gravity. Mutual attraction between bodies in the spirals causes the latter to break into separate sections, the material in each spreading eventually into an elliptical ring of matter bound to the protostar. The relative sizes of the rings are set by the geometry of these logarithmic spiral sections, which double in radius from one to the next. Eventually, each ring aggregates into planetesimals and then a planet whose orbital mean distance is the arithmetic mean of the radii of the edges of the annulus. This explains why the average distances of the planets from the Sun are perfect fourths of successive octaves of undertones. A modified Titius-Bode Law emerges from this scenario that fits the data better than the historical version. The predicted distance of Pluto from Earth differs from the known value by only 0.05%, which is very impressive. It explains why Mercury seems a singular case of the geometric progression of distances by correcting what astronomers mistook in the relationship as the mean distance of Mercury from the Sun, whereas this term really denotes the distance of the asymptotic centre of the logarithmic spiral from the Sun. The musical analogy suggests that planets distribute themselves in groups of eight like the notes of the Pythagorean musical scale. This eight-fold pattern had long been signalled by the breakdown of the relationship for Neptune and Pluto, the ninth and tenth members of the Solar System, but astronomers failed to realise its significance. Instead, they wrongly concluded that the good fit to the Titius-Bode Law was merely coincidental and that this regularity was not a true law. On the contrary, both planets fit the modified law. Moreover, the recent detection of a body about half the size of Pluto at precisely the distance predicted by the modified law for the next planet beyond it is evidence that — as with Uranus, this law once again has predicted the mean distance of a new planet from the Sun.
The logarithmic spiral distribution of matter that generated the planets may be likened to what mathematicians understand as a ‘fractal’ in the sense that it was self-similar, although not continuously so at all scales of distance but only for the discrete series of scales set by each octet. Planetary systems do not contain an arbitrary number of planets but, instead, are made up of octets of planets in which — like the tonic and octave of the Pythagorean musical scale — the most distant member of one octet (octave) is the first member (tonic) of the next outer octet. The geometry of each octet is the same, but rescaled and shifted so that its asymptotic centre coincides with the average distance of the last member of the previous octet. As a result, Neptune and Pluto obey, mathematically speaking, the same kind of Titius-Bode Law as the other planets do, but its parameters are rescaled for the octet to which they belong.
Evidence that this rescaling actually exists (that is, apart from the better fit to the
43
relationship by all ten known members of the Solar System) appears in the form of beautiful, mathematical properties displayed by their theoretical distances that cannot, plausibly, be due to chance because their inherent Pythagorean character would not then have manifested. This is supported by the system of Hebrew Godnames, which have been shown elsewhere to prescribe the mathematics of superstrings and their space-time structure. The way in which the Divine Names determine the octet of planets is unmistakably clear. Amazingly, the predicted distance (in tenths of an AU) between the crossing points of the outer spirals of Earth and Uranus is 248 — precisely the number of transmitter particles predicted by the five superstring theories to mediate their forces! That this, too, cannot be coincidence is indicated by the presence also of the group-theoretical numbers 112 and 128 associated with the superstring gauge symmetry group E8, which denote distances between pairs of planets. Together with the unique Pythagorean character of the Titius-Bode Law when expressed in terms of the average Earth-Sun distance, this has an extraordinary implication for the planet Earth. It is as if, when God the Architect decided to design the Solar System, He had wished to leave the following clue for its future inhabitants about the nature of the subatomic world: placing the end of a tape measure at the edge of the particular spiral arm of the planetary nebula from which Earth was to form, God extended the tape until it reached a spiral arm at the mark numbered 248, at which point He finished His task of sizing the nebula for the first octet of planets and used spirals left over for all remaining planets. In this sense, Earth occupies a unique position amongst the family of planets.
The beautiful, mathematical properties of the Solar System revealed through this article’s presentation of the theory underlying the Titius-Bode Law is evidence that the Solar System is not some galactic backwater created by random chance. Instead, it is a cradle for life — the Divine Life — that bears the signature of its Designer in the geometry of its sacred Tree of Life blueprint, shaped according to the mathematical archetypes embodied in the ten ancient Hebrew, Divine Names. The Pythagoreans taught that form is number. Their principle of apeiron, or the Unlimited (Plato’s principle of the Indefinite Dyad) is at work sizing the arms of the logarithmic spiral according to powers of 2, whilst their principle of peras (Limit) shows itself in the Titius-Bode Law as the number 3 and its multiplication by powers of 2 to define the actual distances of planets relative to the asymptotic centre of the logarithmic spiral. It is the perpetual interplay and balance of these opposite but complementary principles that creates harmonia — the true Pythagorean “music of the spheres” — in the form of the ten octaves of perfect fourths of undertones whose wavelengths are the average distances of the planets from this centre.
“We shall not cease from exploration, and the end of all our exploring will be to arrive where we started and know the place for the first time.”
T.S. Eliot
References
1 Johann Daniel Titius, Betrachtung über die Natur, vom Herrn Karl Bonnet (Leipzig, 1766), pp. 7–8; transl. by Stanley Jaki in “The early history of the Titius-Bode Law,'' American Journal of Physics, vol. 40 (1972), pp. 1014–23.
2 http://en.wikipedia.org/wiki/Ellipse.
3 http://home.att.net/~numericana/answer/geometry.htm#elliptic.
44
5 Phillips, Stephen M. Article 11: “Plato’s Lambda — Its Meaning, Generalisation and Connection to the Tree of Life,” (WEB, PDF).
7 http://www.space.com/scienceastronomy/gemini_keck_020107.html.
8 http://www.space.com/scienceastronomy/astronomy/brown_dwarf_001122–1.html.
9 http://www.solarviews.com/eng/orionnebula1.htm.
10 http://www.seds.org/hst/OriProp4.html.
11 Phillips, Stephen M. Article 15: “The Mathematical Connection Between Superstrings and Their Micro-psi Description: A Pointer Towards M-theory,” (WEB, PDF).
12 Phillips, Stephen M. Article 16: “The Tone Intervals of the Seven Octave Species and Their Correspondence with Octonion Algebra and Superstrings,” (WEB, PDF).
13 See announcement at http://www.cfeps.astrosci.ca/4b7/index.html.
14 See articles at http://www.smphillips.mysite.com.
15 “The Mathematical Connection between Religion and Science,” Stephen M. Phillips (Antony Rowe Publishing, England, 2009).
16 Phillips, Stephen M. Article 1: “The Pythagorean Nature of Superstring and Bosonic String Theories,” (WEB, PDF).
18 In a press release dated Feb. 3, 1999, the International Astronomical Union stated, "No proposal to change the status of Pluto as the ninth planet in the solar system has been made by any Division, Commission or Working Group of the IAU responsible for solar system science. Lately, a substantial number of smaller objects have been discovered in the outer solar system, beyond Neptune, with orbits and possibly other properties similar to those of Pluto. It has been proposed to assign Pluto a number in a technical catalogue or list of such Trans-Neptunian Objects (TNOs) so that observations and computations concerning these objects can be conveniently collated. This process was explicitly designed to not change Pluto's status as a planet." (see: http://www.iau.org/PlutoPR.html). Subsequently, a decision was made, forced by a minority of astronomers, to relegate Pluto to the status of a dwarf planet. According to the demonstration in this article that its mean distance fits well the generalised Titius-Bode law, this undemocratic and unscientific decision is incorrect.
19 http://www.astro.rug.nl/~mwester/aos/aose.html.
20 http://www.ifa.hawaii.edu/faculty/jewitt/kb.html.
21 http://www.ifa.hawaii.edu/faculty/jewitt/papers/ESO/ESO.pdf.
22 http://www.ras.org.uk/html/press/pn99-32.htm.
23 “The Titius-Bode Relation Revisited,” Howard L. Cohen. http://www.fluridastars.org/960coke.html.
45