Article 57

ARTICLE 57

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com

Abstract

According to the Tetrad Principle formulated in Article 1, the first four regular polygons constitute a holistic system. Confirmation of this is provided by the fact that the properties of this geometrical system are analogous to those of well-known sacred geometries revered in various religions. As such, they are prescribed by the gematria number values of the Godnames assigned in Jewish Kabbalah to the ten Sephiroth of the Tree of Life. One of the various parameters characteristic of holistic systems is the number 496, which was found in 1984 to determine the two possible symmetry groups of the forces between superstrings, namely, SO(32) and E₈×E₈. The following question arises: given that the first four enfolded polygons must embody this number in some way, do they embody it in a manner that is compatible with only one of the two groups? If so, it would imply that sacred geometries pick out only one type of superstring as the actual, basic particles making up the physical universe. Other articles have accumulated considerable evidence indicating that sacred geometries favour E₈×E₈ over SO(32). This article confirms this conclusion by showing that, constructed from tetractyses, the first four enfolded polygons have 17 rows of yods with 496 permutations, of which 248 belong solely to the first three enfolded polygons and 248 are shared by all four polygons, where 248 is the dimension of E₈.

1

Table 1. Gematria number values of the ten Sephiroth in the four Worlds.

SEPHIRAH

GODNAME

ARCHANGEL

ORDER OF
ANGELS

MUNDANE
CHAKRA

1
Kether
(Crown)
620 EHYEH
(I am)
21 Metatron
(Angel of the
Presence)
314 Chaioth ha Qadesh
(Holy Living
Creatures)
833
Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
636

2
Chokmah
(Wisdom)
73 YAHWEH, YAH
(The Lord)
26, 15
Raziel
(Herald of the
Deity)
248 Auphanim
(Wheels)
187 Masloth
(The Sphere of
the Zodiac)
140

3
Binah
(Understanding)
67 ELOHIM
(God in multiplicity)
50
Tzaphkiel
(Contemplation
of God)
311
Aralim
(Thrones)
282
Shabathai
Rest.
(Saturn)
317

Daath
(Knowledge)
474

4
Chesed
(Mercy)
72 EL
(God)
31 Tzadkiel
(Benevolence
of God)
62 Chasmalim
(Shining Ones)
428
Tzadekh
Righteousness.
(Jupiter)
194

5
Geburah
(Severity)
216
ELOHA
(The Almighty)
36
Samael
(Severity of God)
131
Seraphim
(Fiery Serpents)
630
Madim
Vehement Strength.
(Mars)
95

6
Tiphareth
(Beauty)
1081
YAHWEH ELOHIM
(God the Creator)
76 Michael
(Like unto God)
101
Malachim
(Kings)
140
Shemesh
The Solar Light.
(Sun)
640

7
Netzach
(Victory)
148
YAHWEH SABAOTH
(Lord of Hosts)
129
Haniel
(Grace of God)
97 Tarshishim or
Elohim
1260
Nogah
Glittering Splendour.
(Venus)
64

8
Hod
(Glory)
15
ELOHIM SABAOTH
(God of Hosts)
153
Raphael
(Divine Physician)
311
Beni Elohim
(Sons of God)
112
Kokab
The Stellar Light.
(Mercury)
48

9
Yesod
(Foundation)
80
SHADDAI EL CHAI
(Almighty Living
God)
49, 363
Gabriel
(Strong Man of
God)
246
Cherubim
(The Strong)
272
Levanah
The Lunar Flame.
(Moon)
87

10
Malkuth
(Kingdom)
496
ADONAI MELEKH
(The Lord and King)
65, 155
Sandalphon
(Manifest Messiah)
280 Ashim
(Souls of Fire)
351
Cholem Yesodoth
The Breaker of the
Foundations.
The Elements.
(Earth)
168

The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers of its letters.

(Numbers in this table referred to in the article will be written in boldface).

2

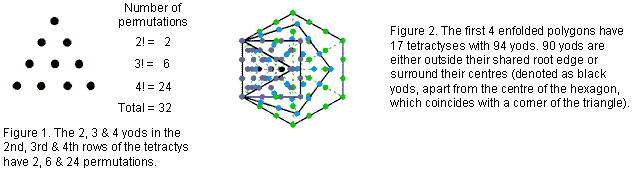
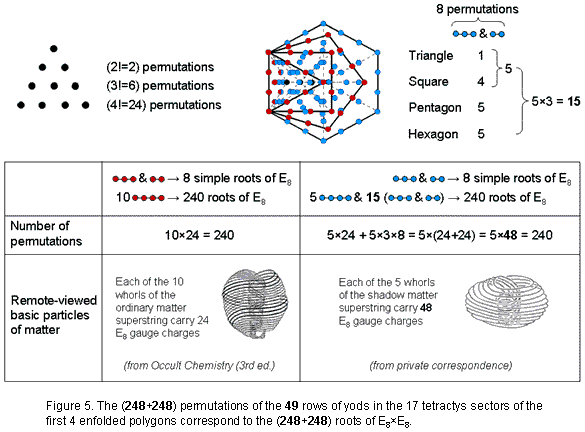
1. 496 permutations of rows in tetractyses of 1st 4 enfolded polygons

The four rows of 1, 2, 3 & 4 yods in a tetractys have, respectively, (1! = 1) permutations, (2! = 2) permutations, (3! = 6) permutations & (4! = 24) permutations (Fig. 1). The three lowest rows have (2+6+24=32) permutations (see also here). This means that 10 objects can be arranged in (1!×2!×3!×4! = 288) different tetractyses, where 288 = 1¹ + 2² + 3³ + 4⁴. When their 17 sectors are tetractyses, the first four enfolded polygons have 94 yods, that is, 90 yods lie outside their shared root edge (Fig. 2). The individual yod populations of these polygons conform to the pattern of integers in the Lambda Tetractys [1], so that they constitute a holistic system.

An n-gon with n tetractys sectors has 6n yods surrounding its centre. They are arranged in 3n rows that have 32n permutations. The n sides of the n-gon have 24n permutations and its 2n second & third rows have 8n permutations. Tabulated below are the numbers of permutations of yods in the root edge and in the 48 rows of the 17 tetractyses in the first four enfolded polygons:

Table 2. Number of permutations of rows in the 17 tetractyses of the first four enfolded polygons.

Polygon

Number of permutations on sides

Number of permutations of 2nd & 3rd rows

Total

Root edge

24×1 = 24

−

24

Triangle

24×2 = 48

8×3 = 24

72

Square

24×3 = 72

8×4 = 32

104

Pentagon

24×4 = 96

8×5 = 40

136

Subtotal

240

96

336

Hexagon

24×5 =120

8×5 = 40

160

Total

360

136

496

Their 49 rows of yods have 496 permutations. Remarkably, this is both the number value of Malkuth, the last Sephirah of the Tree of Life:

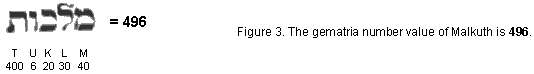
and the dimension of SO(32) and E₈×E₈, the two symmetry groups that generate interactions between superstrings that are free of quantum anomalies [2]. As each permutation of two, three & four yods has its mirror-image counterpart, the 496 permutations consist of 248 permutations and their 248 mirror-images, where 248 is the dimension of E₈. However, the actual division of the 496 permutations into two sets of 248 permutations may be more subtle than this, and we must analyse the contribution of each polygon in more detail. 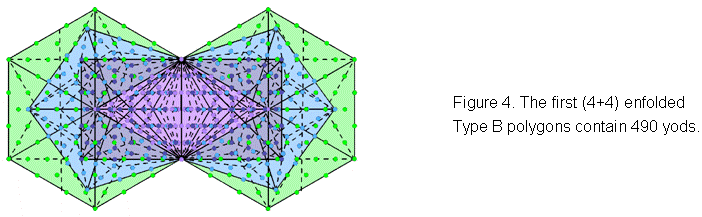The first four enfolded polygons have 49 rows of yods with 496 permutations, showing how EL ChAI, the Godname of Yesod with number value 49, prescribes this number at the heart of superstring theory. In fact, EL ChAI prescribes the first (4+4) enfolded polygons because, when they are all Type B polygons, they possess 490 (=49×10) yods (Fig. 4). The transformation Type A → Type B adds 153 yods to each set of four polygons, where 153 is the number value of ELOHIM SABAOTH, the Godname of Hod.

Table 2 indicates that the first three enfolded polygons have 240 permutations of the yods on their 10

3

sides (24 permutations per side) and 96 permutations of their 24 second & third rows — a total of 336 permutations. This chance-defying conjunction of the superstring structural parameter 336 (the number of circular turns in each revolution of a helical whorl of the UPA) and the superstring dynamical parameters 240 & 496 is amazing. It constitutes powerful evidence for the UPA described by Annie Besant & C.W. Leadbeater being a superstring. This is confirmed by the fact that the 14 sides of the first four enfolded polygons outside their shared root edge with 24 permutations of its four yods also have 336 permutations, so that:

24 + 336 + 136 = 496.

The seven sides of the square & pentagon outside the root edge have (72+96=168) permutations and the seven sides of the triangle & hexagon outside the root edge have (48+120= 168) permutations. The geometry of the first four enfolded polygons naturally allows the division 336 = 168 + 168 that is characteristic of holistic systems [3]. Its counterpart in the superstring is the 336 turns in one revolution of a helical whorl of the UPA and the 168 turns in a half-revolution (scroll down the left-hand column of the table in ref. 4). Alternatively, the three sides of the triangle have 72 permutations and the seven sides of the square & pentagon have 168 permutations. The 72:168 division of the 240 permutations of the sides

4

of the triangle, square & pentagon is a division that is characteristic of the parameter 240 embodied in all holistic systems, corresponding to the 72 roots of E₆, the rank-6 exceptional subgroup of E₈, and the 168 other roots of E₈. Given this remarkable correspondence between the 496 roots of E₈×E₈ and the 496 permutations of the 49 rows of yods in the first four enfolded polygons, the question arises: what eight permutations are the counterpart of the eight simple roots of each E₈? If no natural counterparts exist in the geometry of the first four enfolded polygons, this would be evidence favouring SO(32) over E₈×E₈. However, analysis in previous articles of other sacred geometries have certainly demonstrate their embodiment of the latter symmetry group, and so we should expect the geometry of the first four enfolded polygons to be able to generate these (8+8) permutations. Perhaps, however, one set of polygons corresponds to E₈×E₈ and its mirror image in the other half of the inner Tree of Life corresponds to SO(32)? Given that each side of a polygon generates 24 permutations of their four yods and that the second & third rows of yods in each tetractys generate eight permutations, it seems reasonable to infer that the eight simple roots in one E₈ correspond to the eight permutations in the second & third rows in one of the 17 tetractyses and that the eight simple roots in the other E₈ correspond to the eight permutations in the second & third rows in another tetractys. This leaves 120 permutations in the second & third rows of the remaining 15 tetractyses (120=8×15), as well as the (5×24=120) permutations of the yods in the five sides of the hexagon outside the root edge, making a total of 240 permutations. The two tetractyses should, intuitively speaking, be expected to belong to the simplest polygon — the triangle — because the simple roots of a Lie group are the most basic ones. The former 120 permutations comprise the eight permutations in the second & third rows of the third tetractys in the triangle and the 112 permutations of the second & third rows in the square, pentagon & hexagon (see table). The division: 240 = 112 + 8 +120 = 112 + 128 has its group counterpart in E₈, as now explained. The E₈ root system is a rank 8 root system containing 240 root vectors spanning R⁸. It is irreducible in the sense that it cannot be built from root systems of smaller rank. All the root vectors in E₈ have the same length. It is convenient for a number of purposes to normalize them to have length √2. In the so-called even coordinate system E₈ is given as the set of all vectors in R⁸ with length squared equal to 2 such that coordinates are either all integers or all half-integers and the sum of the coordinates is even. Explicitly, there are 112 roots with integer entries obtained from

(±1, ±1, 0, 0, 0, 0, 0, 0)

by taking an arbitrary combination of signs and an arbitrary permutation of coordinates, and 128 roots with half-integer entries obtained from

(±½, ±½, ±½, ±½, ±½, ±½, ±½, ±½)

by taking an even number of minus signs (or, equivalently, requiring that the sum of all the eight coordinates be even). There are 240 roots in all.

The 28 red yods lining the 10 sides of the triangle, square & pentagon with black yods at their centres form 10 sets of 24 permutations of four yods corresponding to the 240 roots of E₈. The tetractys sector with the root edge as its base has a row of two red yods and a row of three red yods (those yods shared with the two other sectors of the triangle are shown as half red and half blue). These two rows have eight permutations that correspond to the eight simple roots of E₈. Hence, 12 rows of red yods have 248 permutations. The five sides of the hexagon outside the root edge have 14 blue yods and two red yods. They form five sets of 24 permutations of four yods, i.e., 120 permutations. One of the two remaining tetractys sectors in the triangle has two rows with eight permutations; they correspond to the eight simple roots of the second E₈ group. The pair of rows in the other sector of the triangle, the four pairs of rows in the square, the five pairs of rows in the pentagon and the five pairs of rows in the hexagon constitute 15 pairs of rows of yods with (15×8=120) permutations. The number of permutations of the (5+2+2+8+10+10=37) rows of blue yods = 120 + 8 + 120 = 248 . This is the how the pattern of permutations in the rows of yods in the first four enfolded polygons is analogous to the pattern of (248+248) roots in the symmetry group E₈×E₈.

2. Superstrings are either 10-fold or 5-fold

Four rows have 16 permutations corresponding to the 16 simple roots of the two similar E₈ groups and 45 rows have 480 permutations corresponding to their 480 roots. The 10 sides of the first three enfolded polygons generate 240 permutations of red yods (24 per side). There remain five sides of the hexagon and three sets of five pairs of rows, i.e., 35 rows of blue yods, with 240 permutations. They create five sets of seven rows (one side with 24 permutations & three pairs of rows with (3×8=24) permutations. In other words, the 240 roots in one E₈ correspond to 10 sets of 24 permutations and the 240 roots in the other E₈ correspond to five sets of (24+24=48) permutations. Article 53 [5] demonstrates the 10-fold division of the holistic parameter 240 embodied in five sacred geometries. It manifests in the subquark state of the E₈×E₈ heterotic superstring paranormally described over a century ago by Annie Besant & C.W. Leadbeater as the 10 whorls of their UPA. 24 gauge charges of E₈ are spread along each whorl. It was shown in ref. 6 that the seven separate Type B polygons of the inner Tree of Life are composed of

5

240 geometrical elements surrounding the centres of the triangle, square, pentagon & dodecagon and 240 geometrical elements surrounding the centres of the hexagon, octagon & decagon. The former polygons form 10 sets of 24 elements and the latter polygons form five sets of 48. It was proposed in ref. 6 that the former correspond to the 10 whorls of the UPA and that the latter correspond to the five whorls reported by another remote-viewer (private communication) to make up the superstring of shadow matter whose forces are described by the second E₈ group. We now find support for this interpretation in the five-fold pattern of distribution of the 240 permutations of the 37 rows of blue yods. The 10 sides of the triangle, square & pentagon determine the 10 whorls of the superstring of ordinary matter and the five sides of the hexagon outside the root edge, the five sectors of the pentagon and the five remaining sectors of the square & triangle determine the five whorls of the superstring of shadow matter.

There are 360 permutations of the yods in the 15 sides and 136 permutations of the 34 second & third rows. 496 is the 31st triangular number:

1 + 2 + 3 + ... + 31 = 496,

and 136 is the 16th triangular number:

1 + 2 + 3 + ... + 16 = 136.

A pentagon whose five sectors are tetractyses contains 31 yods. 30 yods surround its centre. 31 is the number value of EL (אל), the Godname of Chesed. The value 1 of the letter aleph (א) denotes the centre of the pentagon and the value 30 of lamed (ל) denotes the 30 yods. 15 black yods lie on the sides of the pentagon, inside which are 16 red yods (Fig. 6).

Assigning the integers 1–31 to the 31 yods, starting with 1 assigned to the central yod, the first 16 integers inside the pentagon add up to 136 and the next 15 integers 17–31 assigned to yods on its sides add up to 360. This division is the counterpart of the 496 permutations (see the last row in Table 2). The interior of the pentagon generates the number of permutations of the 34 second & third rows and its boundary generates the number of permutations of the 15 sides of the first four enfolded polygons. Displayed here is a remarkable harmony of number and sacred geometry co-existing with an equally remarkable conjunction of theoretical physics (namely, the number 496 at the heart of superstring theory) and the paranormal observations of Besant & Leadbeater (namely, the number 336 — the number of circular turns in each revolution of a whorl of the UPA revealed by their micro-psi vision).

The 90 yods outside the root edge of the first four enfolded polygons comprise 13 corners of 17 tetractyses and 77 hexagonal yods. The first (4+4) enfolded polygons have (17+17=34) tetractyses with 184 yods made up of (13+13=26) corners outside the root edge and 156 hexagonal yods. 26 is the number value of YAHWEH, the Godname of Chokmah (Hebrew: YHVH), and 156 is the sum of the values of all combinations of the Hebrew letters of YHVH:

YHVH = 26.
Y = 10, H = 5, V = 6.

Y + H + V = 21;

YH + YV + VH + HH = 52;

YHV + YHH + HVH = 57;

YHVH = 26.

Total = 156.

(17+17=34) hexagonal yods are at the centres of the 34 tetractyses and (184−34=150=15×10) yods line their 61 sides, where 15 is the number value of YAH, the older Godname assigned to Chokmah. (150−4=146) yods line the 34 tetractyses outside the root edge. 73 yods outside the root edge line the 17 tetractyses in each set of four enfolded polygons. 73 is the number value of Chokmah. The first (4+4) enfolded Type A polygons have 34 sectors with 61 sides and 28 corners, i.e., 123 geometrical elements. This is the tenth Lucas number L₁₀, i.e., the tenth member of the Lucas series after the first one, L₀ = 2:

2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, ...

6

so that it is determined by the Decad (10). In terms of the Golden Ratio Φ = (1+√5)/2, the nth Lucas number L_n = Φⁿ + (−Φ)⁻ⁿ, so that:

123 = L₁₀ = Φ¹⁰ + Φ⁻¹⁰.

This is how the Golden Ratio and the Decad express the geometrical composition of the first (4+4) enfolded Type A polygons, each half of which embodies the third perfect number 496:*

496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248

at the heart of superstring theory! The second perfect number 28:

28 = 1 + 2 + 4 + 7 + 14

also appears in them as the number of corners of their 34 sectors, whilst the first perfect number 6:

6 = 1 + 2 + 3

is the number of corners of the hexagon, which is the fourth polygon.

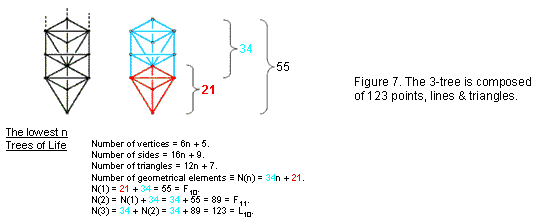
The 3-tree (the lowest three Trees of four or more overlapping Trees of Life) also possesses 123 points, lines & triangles (Fig. 7). Article 32 [7] explains the significance of the 3-tree and its inner form as the Tree of Life map of the human skeleton and its acupuncture meridians.

120 geometrical elements are outside the root edge of the first (4+4) enfolded Type A polygons, where

120 = 2² + 4² + 6² + 8².

The Godname YAH with number value 15 prescribes not only the 15 sides of the first four enfolded polygons and the 15 corners of their 17 sectors but also these 120 geometrical elements because 120 is the 15th triangular number:

1 + 2 + 3 + 4 + ... + 15 = 120.

The Decad also determines this number because it is the sum of the first ten odd integers after 1:

120 = 121 − 1 = 11² − 1 = 3 + 5 + 7 + 9 + 11 + 13 + 15  + 17 + 19 + 21.

See Article 8 [8] for a discussion of the properties of the first four polygons — both separate and enfolded — and their prescription by the Godnames of the 10 Sephiroth. The holistic nature of the first (4+4) enfolded polygons is proved in Article 48 [9].

References

1.         For example, see: http://smphillips.mysite.com/plato%27s-lambda-08.html.

2.         http://smphillips.mysite.com/occult-chemistry-05.html.

3.         http://smphillips.mysite.com/the-holistic-pattern.html.

4.         http://smphillips.mysite.com/real-god-particle.html.

5.         http://smphillips.mysite.com/article-53.html.

6.         http://smphillips.mysite.com/tree-of-life-36.html.

7.         http://smphillips.mysite.com/article-32.html.

8.         http://smphillips.mysite.com/article08.htm.

9.         http://smphillips.mysite.com/article48.htm.

* A perfect number is an integer that is the sum of its divisors.

7