 |
|
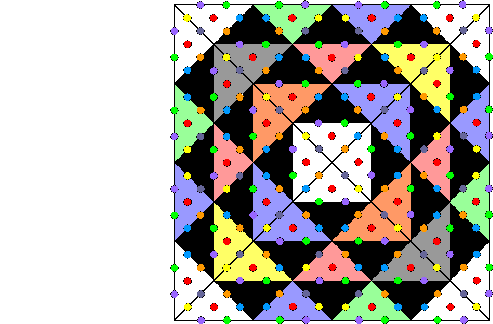
The UPA described by Besant & Leadbeater is a subquark state of the E8×E8 heterotic superstring. |
The tetractys
.png)
The Tree of Life
-
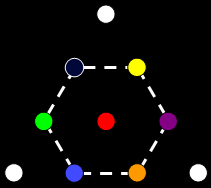
The UPA is composed of 10 closed curves, or "whorls."
- Three ("major") whorls are thicker than the rest.
- Seven "minor" whorls spiral with the major whorls around the vertical axis, separating from the major whorls at the base of the UPA and twisting towards the top in an inner, narrower spiral in the opposite sense to the three major whorls.
- The tetractys is a triangular array of 10 dots, or "yods."
- Three white yods are at the corners of the tetractys.
- Seven coloured yods are at the centre and corners of a hexagon.
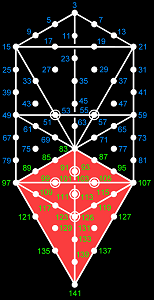
- Ten Sephiroth (Divine qualities) compose the Tree of Life.
- The Supernal Triad comprises Kether, Chokmah & Binah.
- Daath ("knowledge") is the "Abyss" separating the Supernal Triad from the seven Sephiroth of Construction.
.png)
Whorl
Each whorl is a closed helix with 1680 circular turns, or 1st-order spirillae.
|
3 |
23 |
43 |
63 |
|
|
5 7 |
25 27 |
45 47 |
65 67 |
|
|
1680 = |
9 11 13 + |
29 31 33 + |
49 51 53 + |
69 71 73 |
|
15 17 19 21 |
35 37 39 41 |
55 57 59 61 |
75 77 79 81 |
= 
The gematria number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, is 168:
.png)
This is the number of points, lines & triangles below the top of the 1-tree constructed from 19 Type A triangles with 25 sides, i.e., 168 geometrical elements are needed to construct the 1-tree, starting from the point at its apex:
Proof:
Below the apex of the 1-tree are:
(10+19=29) corners of triangles;
(25+ 3×19 = 82) sides of triangles;
(3×19=57) triangles.
Total = 168.
|
|
Each 1st-order spirilla consists of 7
2nd-order spirilla spaced evenly around a circle; each 2nd-order spirillae
comprises 7 3rd-order spirillae, and so on. The 7th-order spirilla is 7 "bubbles in
koilon" spaced evenly around a circle. The 6 higher orders of spirillae represent
the winding of curves around the 6 compactified dimensions predicted by superstring
theory. It appears that the compactified space is
(S1)6 = T6, namely, the 6-dimensional torus,
which is a Ricci-flat, Calabi-Yau space. |
.png)
.png)
The Tree of Life and the 2nd-order tetractys are equivalent representations of holistic systems.
The black hexagonal yods at the centres of the 10 1st-order tetractyses in the 2nd-order tetractys
correspond to the 10 Sephiroth/corners of the 16 tetractyses in the Tree of Life; the 60 white
hexagonal yods in the 2nd-order tetractys at the corners of 10 hexagons correspond to the 60
hexagonal yods in these tetractyses.
|
|
|
(Place cursor over image to enlarge)
|
|
|
|
Two-dimensional & 3-dimensional projections of the 240 root vectors of the rank 8, exceptional Lie group E8 determined by the vertices of the 8-dimensional, Gosset polytope 421. This is one of 255 uniform 8-polytopes with 240 vertices, 6720 edges, 60480 faces, 241920 cells, 483840 4-faces, 483840 5-faces, 207360 6-faces & 19440 7-faces. |
| 240 = |  |
The 240 hexagonal yods in the 48 tetractyses of the 7 separate polygons making up half of the inner Tree of Life denote, in the context of superstrings, the 240 roots/gauge charges of the exceptional Lie group E8 whose associated spin-1 gauge fields determine the forces between the E8′-singlet states of E8×E8′ heterotic superstrings.
.png)
The 1-tree with 19 Type A triangles contains 240 yods other than Sephirothic corners of these
triangles. They denote the 240 roots/gauge charges of the superstring gauge symmetry group
E8.

Interpretation 1
The three major whorls of the UPA correspond to the Supernal Triad of Kether, Chokmah
& Binah (called in Theosophy the 'First, Second & Third Logoi').
72 gauge charges of E8 are spread along the major whorls, 24
per whorl. The seven minor whorls are the manifestation of the seven Sephiroth of Construction
(corresponding to what in Theosophy are called the seven 'Planetary Logoi'). They
carry the remaining 168 gauge charges of
E8. The 240 E8 gauge charges are spread along the 10 whorls of the
UPA/subquark superstring, 24 per whorl. The difference in thickness between the major whorls
and the minor whorls is the result of the breakdown of the symmetry of
E8 into that of E6, the rank-6, exceptional subgroup of
E8, which has 72 gauge charges.
Interpretation
2
Each whorl revolves five times around the axis
about which the UPA spins as a spin-½ fermion. A helical whorl makes 10 half-revolutions
around the axis, each half-revolution being made up of 168 turns. A
half-revolution of all 10 whorls therefore contains 1680 turns — the same number as five
revolutions of a single whorl. Suppose that 24 gauge charges of E8 are spread
along such a half-revolution. Then the 240 gauge charges of E8 are spread
along the 10 half-revolutions of all 10 whorls, i.e., their 50 complete
revolutions, where 50 is the number value of ELOHIM, the Godname of Binah, which is the third
member of the Supernal Triad. The outer and inner halves of the UPA would represent the
E8×E8 heterotic superstring manifestation of 120 gauge charges of
E8, spread along 8400 turns. It corresponds to the compound of two 600-cells with
240 vertices that is the Petrie projection of the Gosset polytope, whose 240 vertices
determine the 240 root vectors in the 8-dimensional lattice space of E8. 70 turns
(7 per whorl) represent a single charge, which is the source of a 10-dimensional gauge field.
Seven turns are associated with each of the 2400 components of the 240 10-dimensional
E8 gauge fields: 16800 = 2400×7. According to this alternative view, instead
of the gauge charges being smeared out over single whorls, 24 to a whorl, they are spread out
along all 10 whorls, 24 to a half-revolution of them. Three whorls are different to the other
seven because they correspond to, or generate, the three spatial components of every
10-dimensional gauge field that are measured along the three large-scale dimensions of space.
The seven minor whorls correspond to the time and spatial components of each gauge field
measured along the six compactified dimensions.
Which is the correct interpretation? The fact that each 600-cell has 1200 faces that, taken separately, have 8400 corners, sides & triangles corresponding to the 8400 turns in the inner or the outer half of the UPA supports Interpretation 2 as the more natural one because it explains not only why the UPA has two halves but why each half comprises five revolutions, each 600-cell being a compound of five 24-cells. In the case of interpretation 1, five whole whorls would have to correspond to each 600-cell, so that a whorl would have to correspond to a 24-cell, which leaves unexplained why it has an inner and an outer half and why each half has five half-revolutions. As shown on #3 of 4-d sacred geometries, sacred geometries comprise 240 structural components (yods or geometrical elements) that can be grouped naturally into a pair of five sets of 24. Each "half" of these sacred geometries has its 4-dimensional counterpart in the 600-cell, so that we can feel sure that the latter does, indeed, correspond to an inner or outer half of the UPA rather than to five complete whorls. It suggests, therefore, that a 24-cell defines a half-revolution of all 10 whorls of the UPA rather than one complete whorl.

|
|
Each whorl in the UPA is a helix with 1680 circular turns, or "1st-order spirillae." It is 10-dimensional, the six higher orders of spirillae being helices that wind around the six compactified dimensions (actually progressively smaller circles) predicted by superstring theory. A dimension is represented by a Tree of Life, so that a whorl is geometrically represented by 10 overlapping Trees of Life. As the microscopic Tree of Life, the UPA has 10 whorls corresponding to the 10 Sephiroth. Each Sephirah can be represented by a Tree of Life with 10 Sephiroth, each of the latter by a Tree of Life, and so on. This means that a whorl can be mapped by both a single Tree of Life and 10 overlapping Trees of Life; the latter is merely the more differentiated version of the former. Just as the UPA is a whole, Kabbalistically speaking, so, too, is each whorl. |
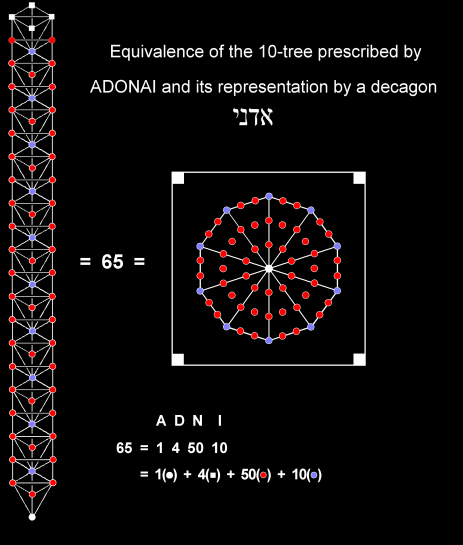
The Godname of Malkuth — the physical manifestation of the Tree of Life blueprint — is ADONAI. Its number value is 65, which is the number of Sephirothic levels (white, red & blue corners of triangles) in the 10-tree. This is equivalent to a tetractys-divided decagon that is enclosed in a square. ADONAI prescribes the 10 dimensions of space-time predicted by superstring theory and mapped by 10 Trees of Life. EL ("God"), the Godname of Chesed with number value 31, also prescribes them because the 10-tree has 127 triangles, where 127 is the 31st prime number. EHYEH ("I am"), the Godname of Kether wiith number value 21, prescribes the 10-tree because each side pillar of it has 21 Sephirothic levels.


Each of the 10 whorls spirals five times around the axis of the UPA. Each revolution of the 10 whorls comprises 3360 helical turns (1st-order spirillae), 336 per whorl. An outer or inner half-revolution of a whorl comprises 168 turns and a quarter-revolution comprises 84 turns.
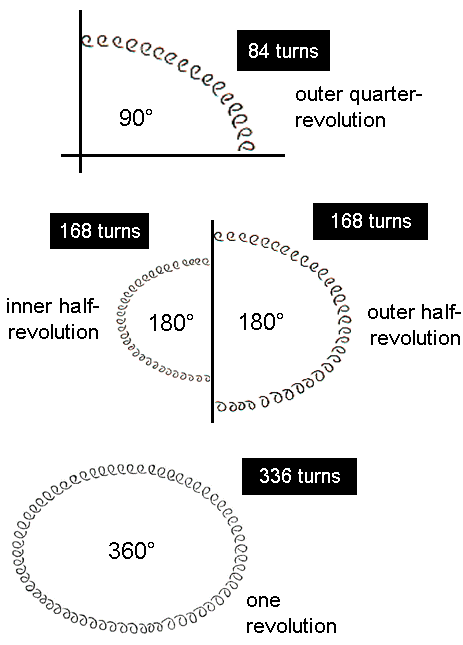
The seven enfolded polygons of the inner Tree of Life contain 3360 yods when their sectors are 2nd-order tetractyses.
84
= 12 + 32 + 52 + 72. 336
= 42 + 82 + 162 = 22×84 = 22 + 62 + 102 + 142.
The 3-d Sri Yantra is shaped by the same number (336) as the number of turns in one revolution of a
helical whorl of the UPA/subquark superstring. The 168 yods lining each half
of the Sri Yantra denote the 168 turns in an outer or inner half-revolution
of a whorl.
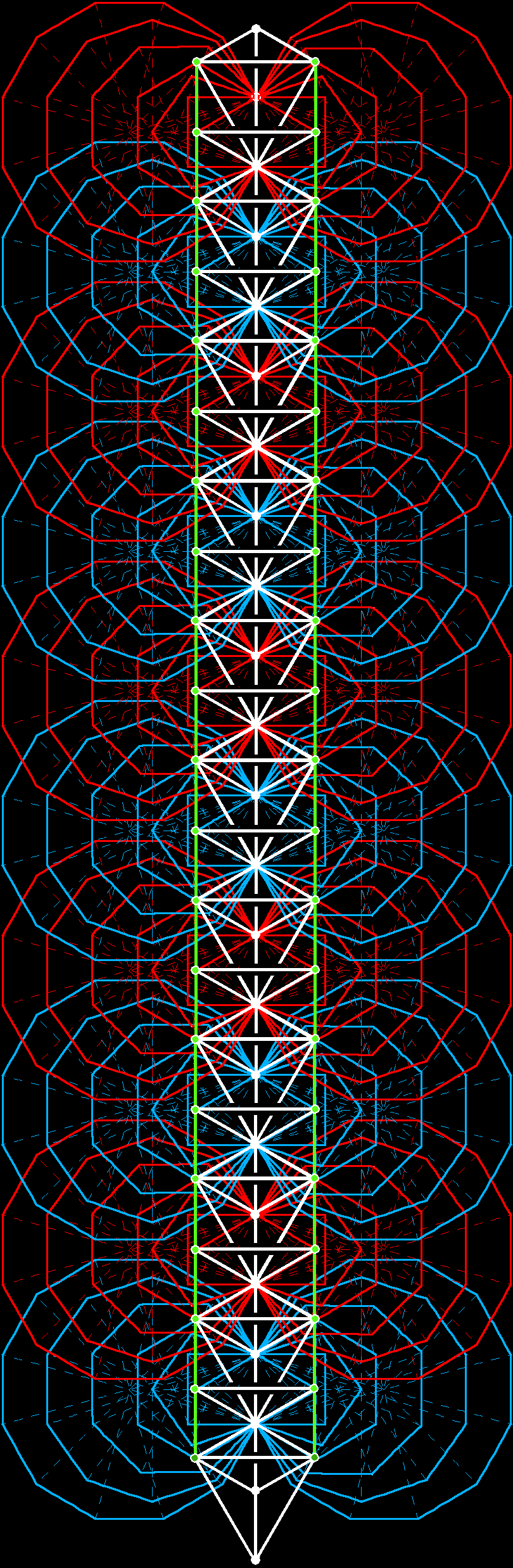
Divided into their sectors, the (70+70) polygons enfolded in 10 overlapping Trees of Life are composed of 3360 points, lines & triangles that are unshared with the outer Trees (shared geometrical elements are coloured green). Each set of (7+7) enfolded polygons has (168+168=336) geometrical elements that are unshared with its outer Tree of Life.
|
|
|
The 10 helical whorls of the UPA have 16800 circular turns. |
.gif)
16800 yods surround the centre of the 7-pointed star, where 16800 = 7×2400.
Every point of the star is a
parallelogram constructed from tetractyses with
49 yods lining each
side. It contains (492−1=2400) yods outside a corner.
| Number of white yods = 3×1680 = number of turns in the three major whorls of the UPA. |
| Number of coloured yods = 7×1680 = number of turns in the seven minor whorls of the UPA. |
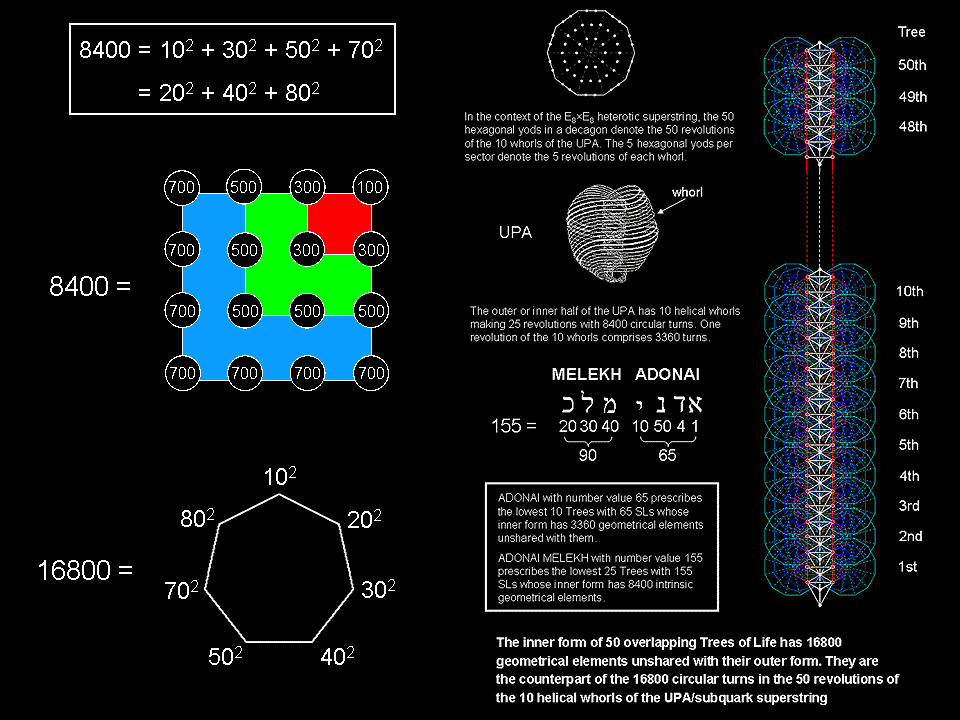
The Godname ELOHIM with number value 50 prescribes the 16800 turns in the 50 revolutions of the 10 helical whorls of the UPA/subquark
superstring. The Godname ADONAI MELEKH with number value 155 prescribes the 8400 turns in an outer or inner half of these 10 whorls.
|
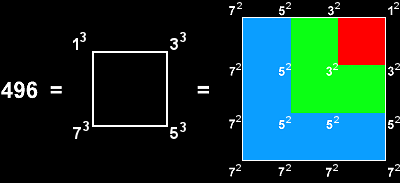
Superstring theory requires the symmetry group of the unified, quantum anomaly-free interaction between heterotic superstrings to be either SO(32) or E8×E8, both groups having dimension 496. In the latter case, heterotic superstrings of ordinary matter have a unified force that is described by the exceptional Lie group E8 with dimension 248. |
There are 248 hexagonal yods in a square with 2nd-order tetractyses as its sectors. Each yod symbolizes a root of E8, the rank-8, exceptional Lie group.
The square also provides an arithmetic representation of the dimension 496 of the two possible superstring gauge symmetry groups SO(32) & E8×E8:
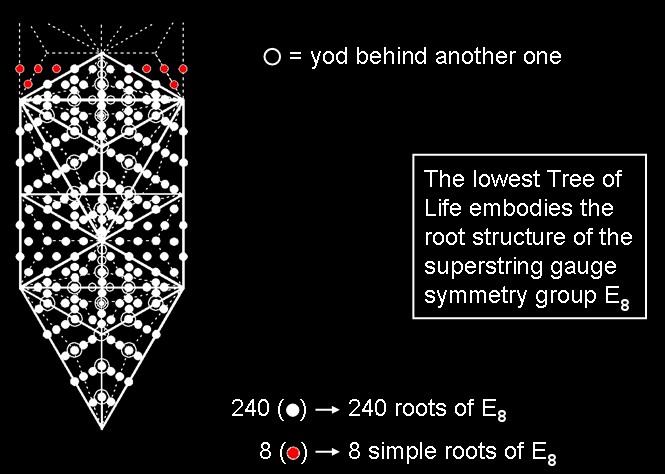
There are 248 yods below the top of the 1-tree with its triangles turned into Type A triangles. The eight red yods outside the 1-tree denote the eight simple roots of E8 and the 240 white yods other than Sephiroth denote its 240 roots.
Superstring theory requires the symmetry group of the unified, quantum anomaly-free interaction between heterotic superstrings to be either SO(32) or E8×E8, both groups having dimension 496. In the latter case, heterotic superstrings of ordinary matter have a unified force that is described by the exceptional Lie group E8 with dimension 248.
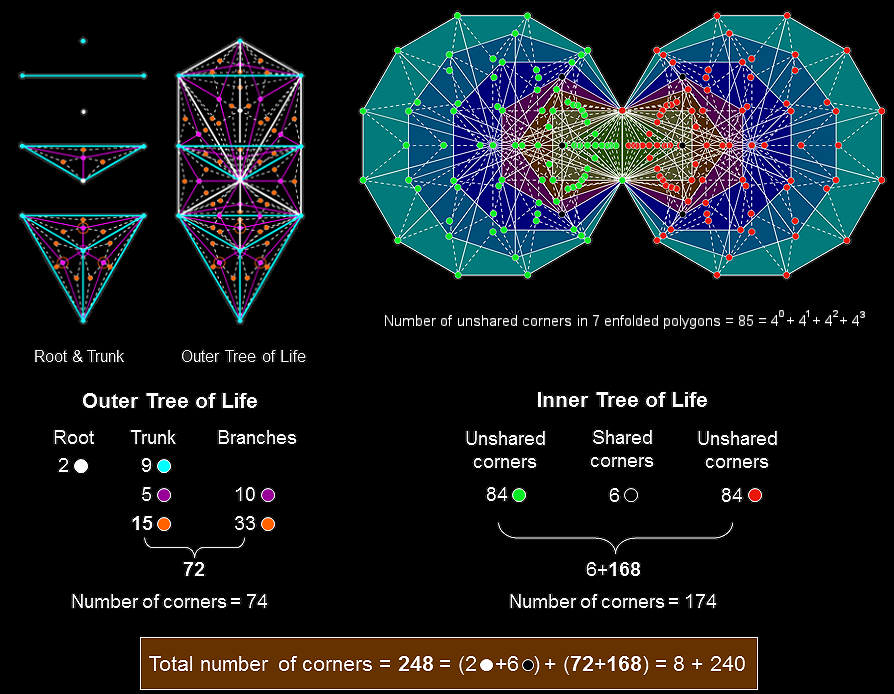
A Type B triangle is composed of 9 triangles with 3 external corners and 4 corners that are inside it. The 16 Type B triangles of the outer Tree of Life have 10 corners on their 22 sides and (16×4=64) internal corners of their (16×9=144) triangles with (16×12=192) sides. The outer Tree of Life comprises its root, its trunk and its branches. In terms of the 74 corners, the root consists of two corners whose projection onto the plane containing the (7+7) enfolded polygons of the inner Tree of Life are the endpoints of their shared root edge. One corner is located at Daath, which is the centre of the triangle formed by Chokmah, Binah & Tiphareth. The other corner coincides with Tiphareth, which is the centre of the Tree of Life in both a geometrical and a metaphysical sense. It is where the root joins the trunk of the Tree of Life, which is the sequence:
The 7 enfolded, Type B polygons have 47 sectors with 41 corners. Their (47×3=141) triangles have (41+47=88) corners (86 outside the root edge). The (7+7) enfolded, Type B polygons have (2×141=282) triangles with (2 + 2×86 = 174) corners. 282 is the number value of Aralim, the Order of Angels assigned to Binah. The centre, top and bottom of each hexagon coincide with corners of triangles belonging to the outer Tree of Life. These six white corners are shared and (174−6=168) corners are unshared. (168/2=84) corners (turquoise or pink) are associated with each set of 7 enfolded polygons, which have 85 unshared corners, where
|
|
|
|
3-d projection of rotating 600-cell |
3-d projection of rotating 600-cell |
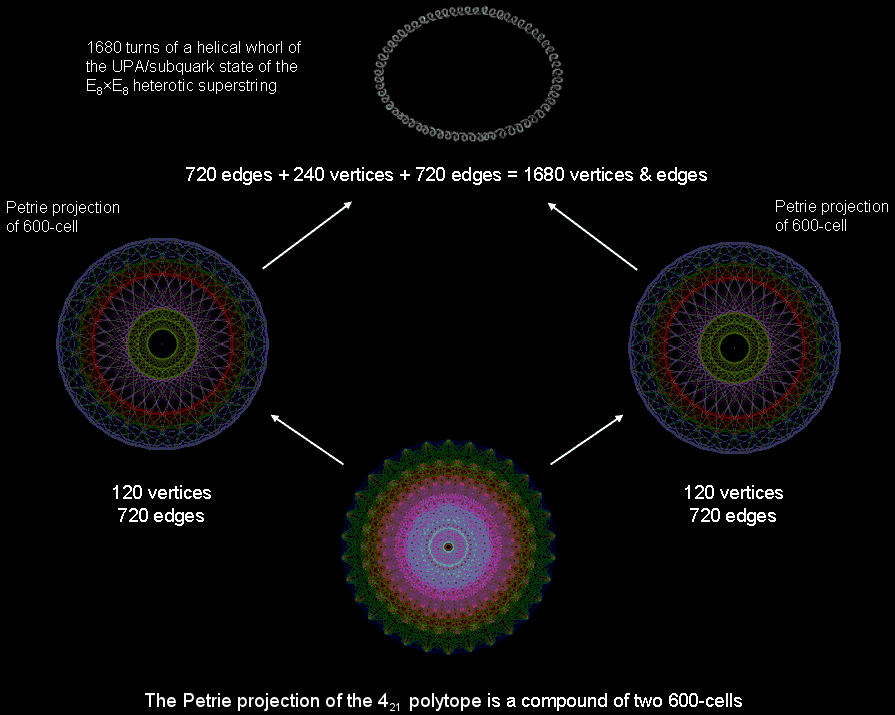
| It is no coincidence that sacred geometries reproduce the 720:240:720 pattern in the vertices & edges in the compound of two 600-cells that is the Petrie projection of the 421 polytope. Rather, what is appearing in this polytope is a universal archetype that is embodied in ancient sacred geometries and which manifests in space-time as the 1680 turns of each helical whorl making up the UPA/subquark state of the E8×E8 heterotic superstring. |

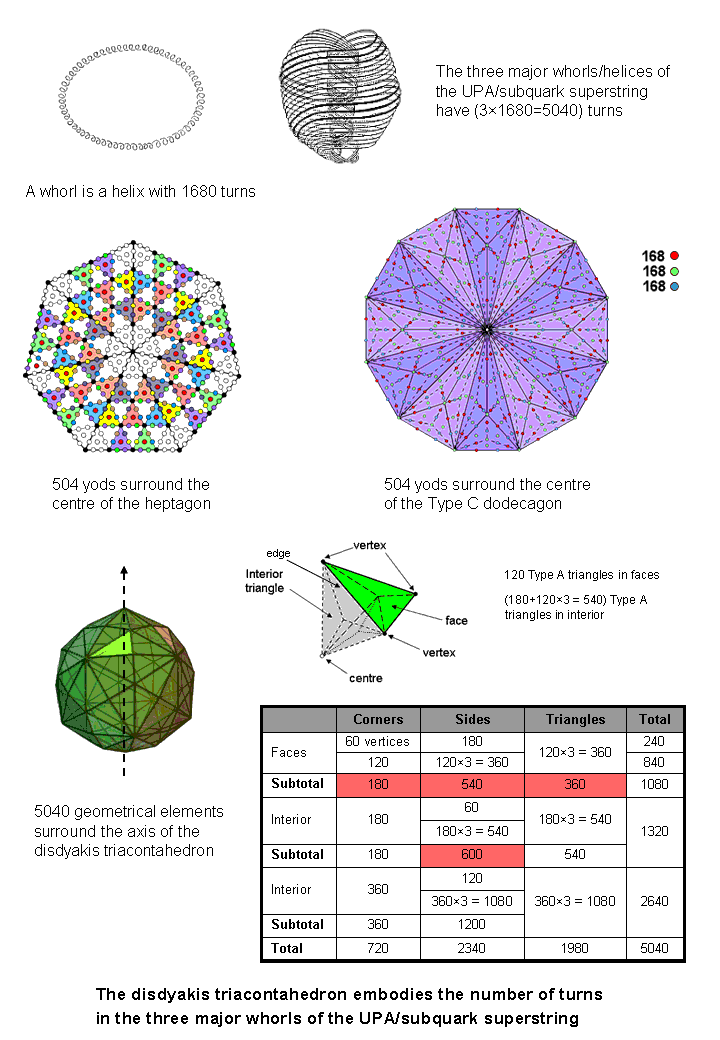
Correspondence between the geometrical or yod compositions of the first four Platonic solids,
the disdyakis triacontahedron, the inner & outer Trees of Life and the inner form of the 10-tree
| 412 − 1 = 3 + 5 + 7 +... + 81 = 1680. |
| 712 − 1 = 3 + 5 + 7 +... 83 +... + 141 = 5040 = 3×1680. |
| 5040 − 1680 = 3360 = 83 + 85 + 87 +... + 141 = 2×1680. |
The sum of the 70 odd integers after 1 assigned to the 70 yods of the Tree of Life = 5040. This is the number of turns in the three helical major whorls of the UPA/subquark superstring. It is the sum
of the first 40 odd (blue) integers 3-81 after 1 assigned to the 40 yods outside the (red) Lower Face and the next 30 odd (green) integers 83-141 assigned to the 30 yods in the Lower Face.
The subquark state of the E8×E8 heterotic superstring remote-viewed by the Theosophists Annie Besant & C.W. Leadbeater over a century ago consists of 10 closed curves, or "whorls." They bear a correspondence to the 10 Sephiroth of the Tree of Life. The three major whorls correspond to the Supernal Triad and the seven minor whorls are the counterpart of the seven Sephiroth of Construction. Each whorl is a helix with 1680 circular turns. The three major whorls have (3×1680=5040) turns.
Sacred-geometrical embodiment of 504 & 5040
Heptagon
When the seven sectors of a heptagon are 2nd-order tetractyses, 504 yods surround its
centre.
Type C dodecagon
When the 12 sectors of a Type C
dodecagon are constructed from tetractyses, 504 yods surround its centre. They can be grouped into
three sets of 168 yods (coloured red, green & blue).
Disdyakis triacontahedron
The disdyakis triacontahedron has 62 vertices (60 vertices surrounding an
axis passing through two opposite vertices). Its 120 triangular faces have 180 edges. Their
(120×3=360) sectors have (360+180=540) sides. The number of geometrical elements in the faces that
surround the axis = 60 + 120 + 540 + 360 = 1080.
Each edge and each side of a sector in the green faces of the disdyakis triacontahedron are sides of internal grey triangles with the centre of the polyhedron as their shared corner. The (180+360=540) internal triangles have (540×3=1620) sectors with (60 + 120 + 540×3 = 1800) internal sides & 540 internal corners surrounding the centre, i.e., 3960 geometrical elements. The number of geometrical elements in the faces and interior that surround the axis = 1080 + 3960 = 5040. They include 1680 elements (red cells) either in the faces (1080) or sides (600) of sectors of internal triangles created by the edges of the disdyakis triacontahedron, leaving 3360 elements (1680 elements in each half of the polyhedron).* This is the polyhedral counterpart of the 1680 helical turns in the first major whorl and the 3360 turns in the second & third major whorls.
* Alternatively, surrounding the axis are 1680 geometrical
elements comprising 180 corners of sectors in the faces, 180 edges & 1320 geometrical elements
in the internal triangles created by edges. This totals 1680 elements, leaving 3360
elements.
|
|
|

3-dimensional projection of a rotating 24-cell.

3-dimensional projection of a rotating
600-cell.
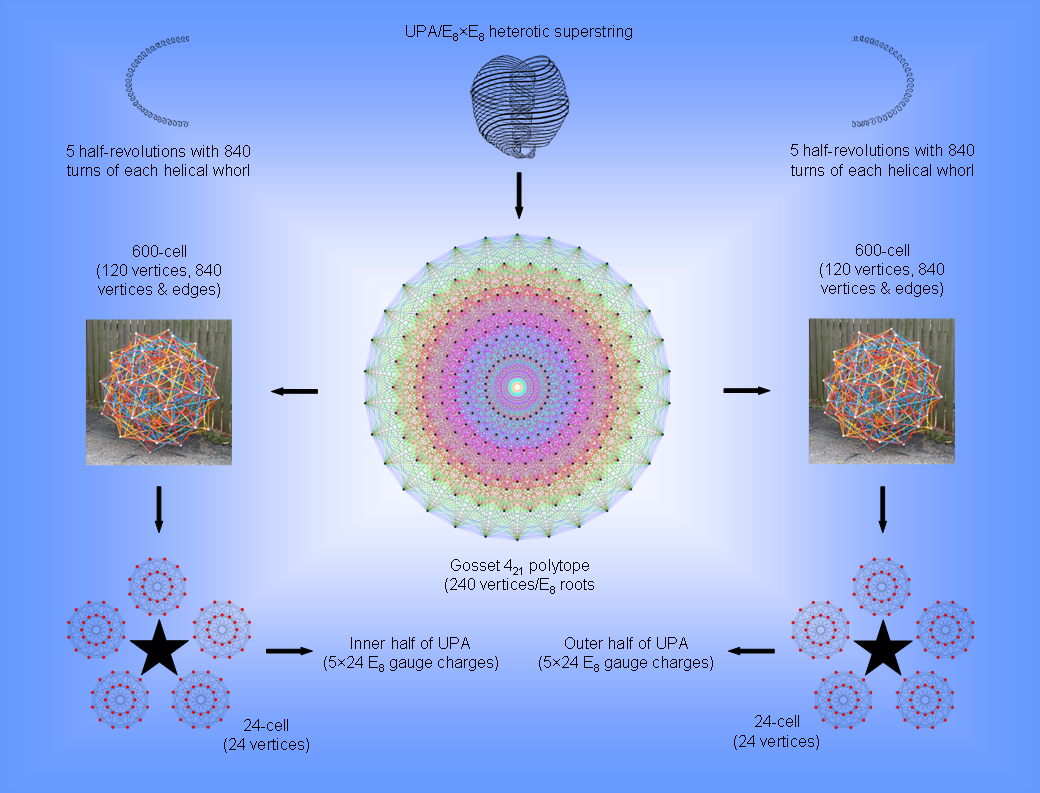
The 240 vertices of the 421 polytope coincide with the positions of the 240 roots of E8, the rank-8, exceptional Lie group. The 4-d projection of this 8-d polytope is a compound of two 600-cells. The 120 vertices of a 600-cell can be partitioned into those of five disjoint 24-cells. As each vertex of the 421 polytope defines one of the 240 root vectors of E8, there is a geometrical basis for dividing the 240 gauge charges corresponding to these roots into 10 sets of 24, each set being represented by the 24 vertices of a 24-cell. The outer half of the UPA is the counterpart of one 600-cell, the 120 gauge charges denoted by the 120 vertices of the five 24-cells being spread out along the five half-revolutions of the 10 whorls in this half. The inner half of the UPA is the counterpart of the other 600-cell. The 2½ revolutions (five half-revolutions) of the whorls that make up each half are the counterpart of the five 24-cells in each 600-cell. The 840 vertices & edges in each 600-cell are the geometrical counterpart of the 840 circular turns in the five half-revolutions of the outer or inner half of each helical whorl. The 1680 vertices & edges belonging to the compound of two 600-cells in the Gosset polytope are the counterpart of the 1680 circular turns in each helical whorl of the UPA. 70 turns "carry" an E8 gauge charge: 1680 = 24×70.
This correlation is irrefutable evidence that the UPA paranormally described over a century ago is a state of the E8×E8 heterotic superstring (see Article 62 for more details).
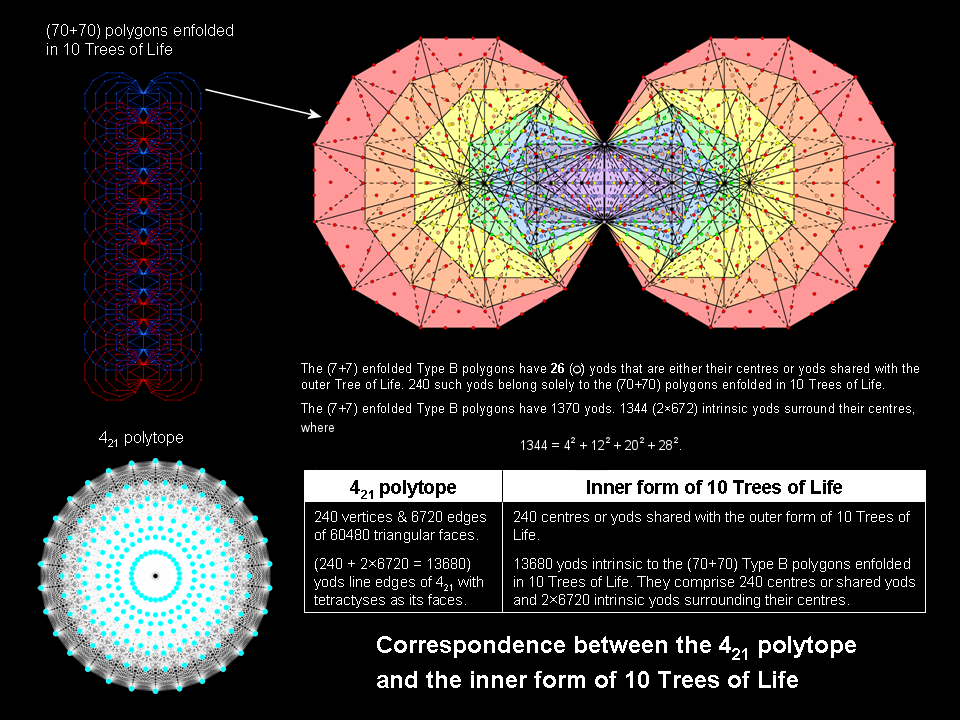 |
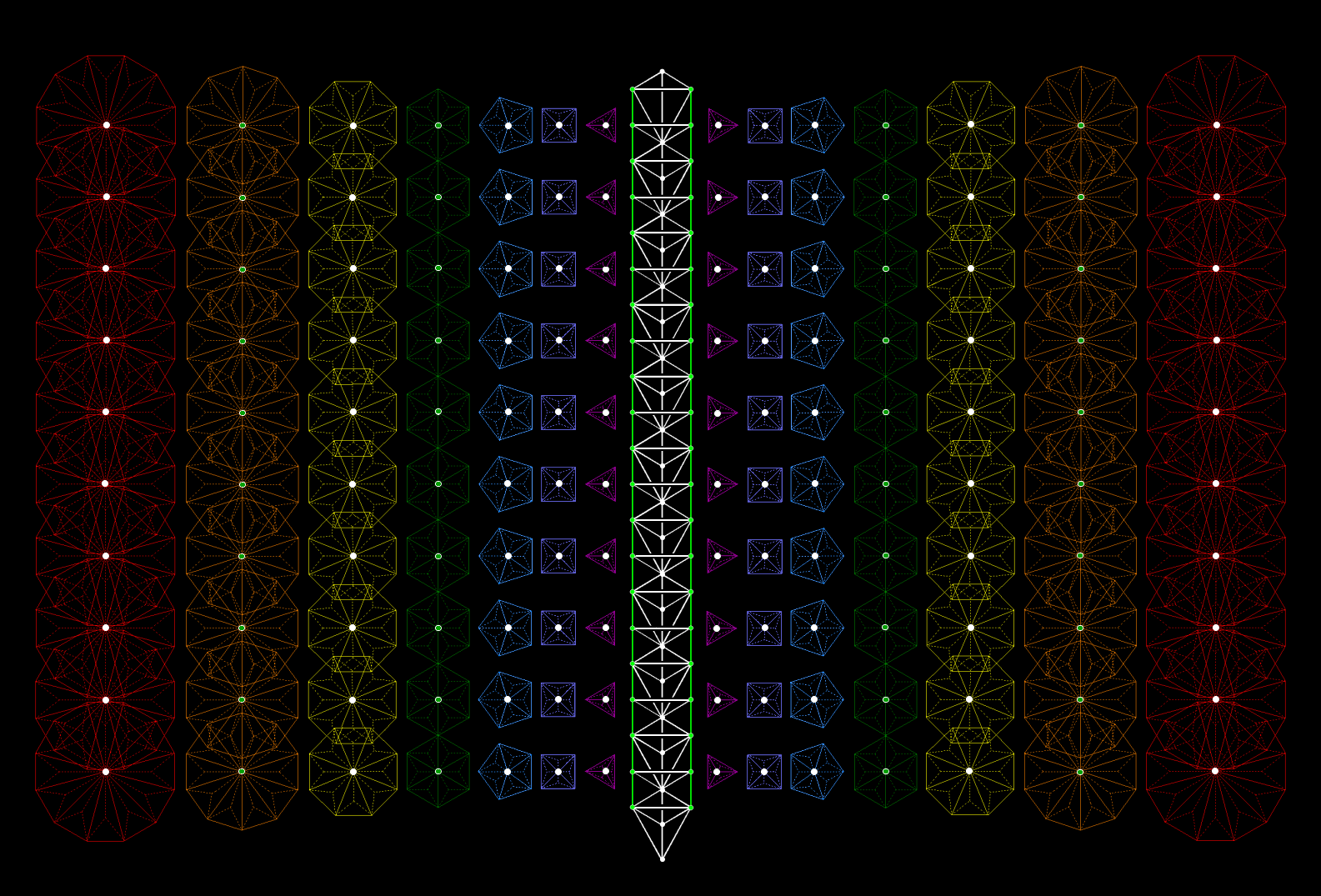
The 421 polytope is the 8-dimensional polytope counterpart of the inner form of 10 overlapping Trees of Life when the (70+70) regular polygons enfolded in the latter are Type B. Each set of (7+7) enfolded polygons embodies the number 137 that determines the fine-structure constant because its yod population is that of 137 tetractyses. The topmost corners of the two hexagons coincide with the lowest corners of the hexagons enfolded in the next higher Tree. This leaves 1368 yods intrinsic to each Tree, i.e., 13680 yods are intrinsic to 10 Trees of Life. They correspond to the 13680 yods lining the 6720 edges of the 421 polytope with tetractyses as its 60480 faces: 240 vertices + 6720×2 hexagonal yods = 13680. The 7 black yods in each hexagon
coincide with yods on the two side pillars of the outer Tree of Life.
Six other black yods are centres of the other polygons in each half of the
inner Tree of Life. 26 black yods in both halves are either
centres of polygons or shared with the outer
Tree. Of these, two are shared with the
hexagons enfolded in the next higher Tree. This means that 24 black yods per
set of (7+7) enfolded polygons are either centres or shared yods. There are
240 yods in the (70+70) polygons enfolded in 10 Trees of Life that are either
centres or shared yods. There are 13440
yods (6720 pairs) intrinsic to these 140 polygons that
surround their centres. They correspond to the 13440 hexagonal yods on the 6720 edges of the
421 polytope. Discounting coincidence as too improbable, what do these correspondences imply? 1. E8×E8 heterotic
superstrings exist; |
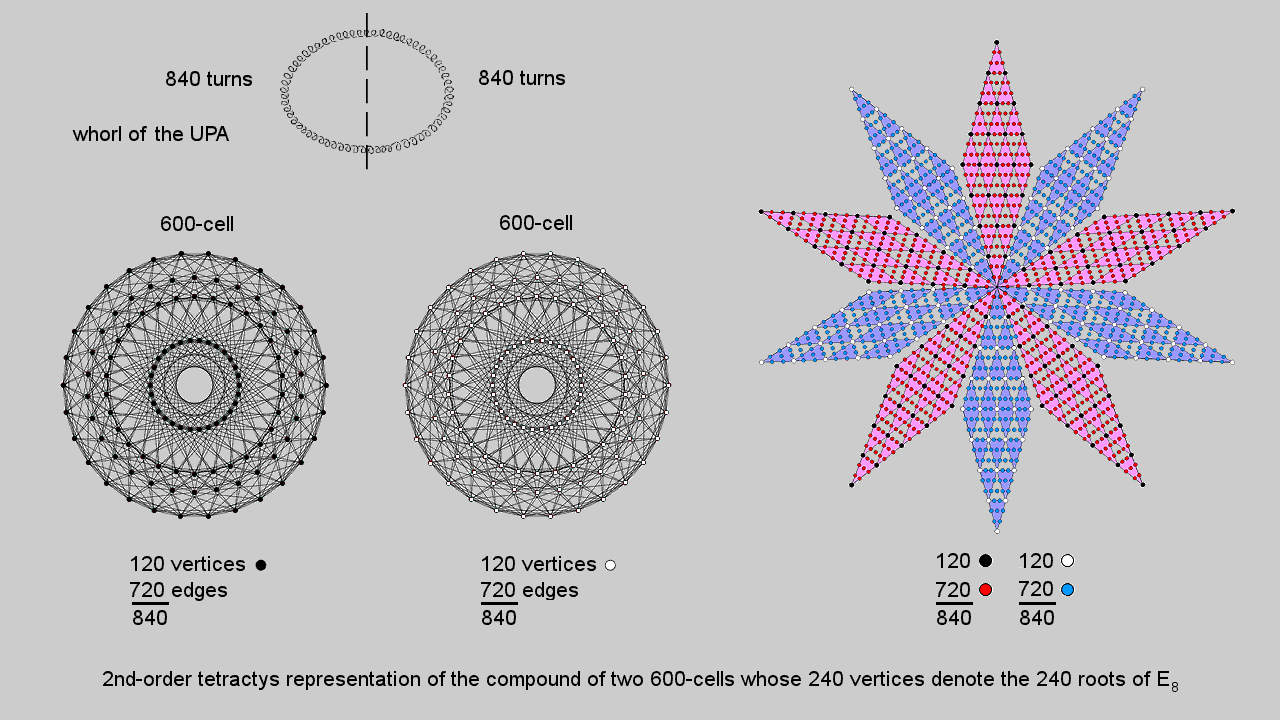
A 2nd-order tetractys contains 85 yods, where
85 = 40 + 41 + 42 + 43.
Including the yods at the centres of the six triangular gaps between the 1st-order tetractyses in the 2nd-order tetractys generates a triangular array of 91 yods, where
91 = 12 + 22 + 32 + 42 + 52 + 62.
13 yods line each side of the array, so that a parallelogram made up of two triangular arrays of 91 yods placed back to back contains (91+91−13=169) yods. Surrounding the centre of a 10-pointed star whose points are these arrays are 1680 yods. Each 5-pointed star has 840 yods. Each point of the star contains 120 corners of 1st-order tetractyses and 720 hexagonal yods. The red 5-pointed star contains 120 black corners of 1st-order tetractyses and 720 red hexagonal yods. The blue 5-pointed star contains 120 white corners of 1st-order tetractyses and 720 blue hexagonal yods. The 1680 yods in the 10-pointed star comprise 240 corners of tetractyses and 1440 hexagonal yods. Compare this with the fact that a 600-cell is a polychoron with 120 vertices and 720 edges. The 10-pointed star is a representation of the compound of two 600-cells with 240 vertices and 1440 edges, each 5-pointed star representing a 600-cell. The 240 corners of 1st-order tetractyses denote the 240 vertices of the compound and the 1440 hexagonal yods denote the 1440 edges.
Each point of the star contains 24 corners of 1st-order tetractyses. They correspond to the 24 vertices of a 24-cell, each 5-pointed star representing the compound of five disjoint 24-cells that make up a 600-cell. We saw in the last section that the 24 vertices of a 24-cell consist of the eight vertices of a 16-cell and the 16 vertices of an 8-cell. In the point of the 10-pointed star, they correspond to the eight corners of tetractyses outside the corner shared between star points that line two adjacent sides of the parallelogram and to the remaining 16 corners.
This 10-pointed star representation of the 240 vertices of a compound of two 600-cells as the 4-dimensional projection of the 240 roots of E8 mapped by the 8-dimensional 421 polytope is a particularly clear demonstration of the 10-foldness of this number displayed by sacred geometries, as explained in #2 of 4-d sacred geometries. It should not, therefore, come as a surprise that the 1680 turns of each helical whorl of the UPA/heterotic superstring are generated in 10 half-revolutions (180°). The outer five half-revolutions of a whorl with 840 turns are represented by the 840 yods (120 corners, 720 hexagonal yods) in one 5-pointed star and its inner five half-revolutions with 840 turns are represented by the 840 yods in the other 5-pointed star. However, if we want to retain the correspondence between the 240 corners of tetractyses and the 240 vertices of the two 600-cells determining the 240 roots of E8, this correspondence cannot be interpreted as referring to a single whorl. Rather, each point in the 10-pointed star must correspond to either a whorl or (as we concluded in earlier sections of 4-d sacred geometries) a half-revolution of all 10 whorls of the UPA, which is represented by the whole star because the UPA "carries" the 240 gauge charges of E8 corresponding to its roots.
The counterparts of this in the inner form of 10 Trees of Life (see right-hand picture) are the 1680 corners of the 2820 triangles in the (70+70) Type B polygons that are unshared with them. They comprise (120+120=240) red corners of the sectors of the 20 dodecagons and 720 remaining corners in each set of 70 enfolded polygons that are unshared with the outer Trees of Life. This demonstrates in an unequivocal way the Tree of Life basis of the 120:720 division in vertices & edges of each 600-cell.

The 421 polytope has 240 vertices and 6720 edges.
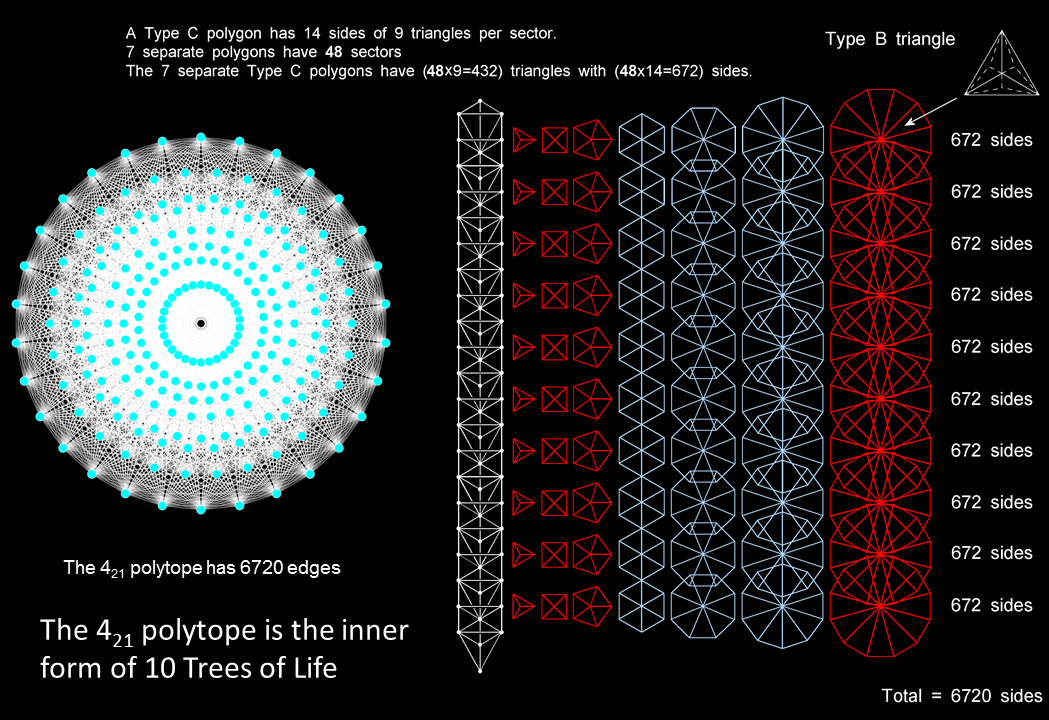
The 70 regular polygons enfolded in the inner form of 10 Trees of Life have 6720 sides when they are separate and Type C, i.e., when every sector is a Type B triangle. They correspond to the 6720 edges of the 421 polytope. It is evidence that the latter is the 8-d polytopic version of the inner form of 10 Trees of Life. The implication from this correlation of a hidden 10-foldness in the 421 polytope is confirmed by the mathematical fact that its 4-d Coexeter plane projection is a compound of two concentric 600-cells, each of which is a compound of five 24-cells.
The two halves of the 421 polytope, each with 3360 edges, correspond to the two sets of 35 polygons (red & blue), each set being composed of 2160 triangles with 3360 sides.
There are 240 white dots & white sides of triangles in every 10 overlapping Trees of Life that either belong solely to their outer form or are white centres of 100 of the 140 Type B polygons associated with these Trees that remain "pure" centres when the polygons become enfolded (note: centres of hexagons become corners of the triangles and centres of decagons become corners of pentagons). Green corners & sides of triangles in every 10 Trees become shared with enfolded polygons, whilst 40 green centres of 20 hexagons & 20 decagons coincide with corners of other polygons when they all become enfolded. 6720 corners & sides of the 2820 (=10×282) triangles in the 140 separate Type B polygons surround their centres.* 282 is the number value of Aralim, the Order of Angels assigned to Binah, and 140 is the number of Malachim, the Order of Angels assigned to Tiphareth.
|
240 unshared, white corners & sides of triangles in 10 Trees of Life or "pure" centres of 100 polygons |
→ 240 vertices of the 421 polytope. |
|
6720 corners & sides of triangles in inner form of 10 Trees of Life |
→ 6720 edges of the 421 polytope. |
Here are two inferences from this amazing correspondence:
-
The 421 polytope, whose 240 vertices are the root vectors of E8, is a holistic system conforming to the archetypal geometry of the Tree of Life blueprint.
-
The E8×E8 heterotic superstring is the material manifestation in the subatomic world of the divine paradigm.
* Proof: There are 7 corners & sides of triangles per sector, 48 sectors per set of 7 polygons and 10 sets of (7+7) polygons in the inner form of 10 Trees of Life. Total number of their corners & sides = 10×(48+48)×7 = 6720.
.png)
|
Spread along the 16800 circular turns or circularly polarised waves in the 10 helical whorls of the UPA (E8×E8 heterotic superstring) are the 240 gauge charges of E8. Each whorl |
| comprises 1680 turns and winds five times around the UPA's axis of spin. Each half-revolution of a whorl contains 168 turns, so that a half-revolution of all 10 whorls contains 1680 turns. |
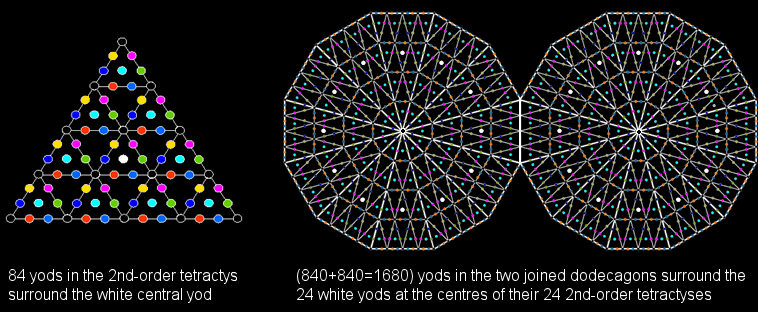
The dodecagon is the last of the seven types of regular polygons making up the inner Tree of Life. When their 24 sectors are turned into 2nd-order tetractyses, there are 840 yods outside their
shared root edge that surround the 12 white centres of the 12 2nd-order tetractyses in each dodecagon. This is ten times the number of yods surrounding the centre of a single 2nd-order tetractys.

16800 yods outside their root edges surround the white yods at the centres of the 240 2nd-order tetractyses that make up the (10+10) dodecagons enfolded in 10 overlapping Tree of Life.
The number of yods surrounding the centres of the 120 2nd-order tetractyses in each set of 10 dodecagons = 8400 = 102 + 302 + 502 +702. They denote the 8400 turns in the outer/inner halves of the 10 whorls of the UPA.
16800 yods outside the root edges of the (10+10) dodecagons enfolded in 10 overlapping Trees of Life surround the white centres of the 240 2nd-order tetractys sectors of these dodecagons. They denote the 16800 circular turns of the 10 helical whorls of the UPA (subquark state of the E8×E8 heterotic superstring). These 240 white centres denote the 240 gauge charges of E8. The 24 white centres per pair of dodecagons denote the 24 E8 gauge charges that are spread along a half-revolution of all 10 whorls, a Tree of Life mapping a half-revolution. This is another example of the 10-fold division of sacred geometries (see Article 53 and #2 in 4-d sacred geometries). In the subatomic world, this 10×24 pattern expresses the spreading of the 240 gauge charges of E8 along the 10 half-revolutions of all 10 whorls of the UPA, the 24 charges per half-revolution being spread along 1680 turns.
.png) |
|
YAH (יה) is the shorter form of YAHWEH (יהוח), which is the complete Godname of Chokmah, the second Sephirah of the Tree of Life. Its gematria number value is 15. As
152 − 1 = 224,
15(152−1) = 15×224 = 3360 = 153 − 15.
This is the number of turns in one revolution of the 10 whorls of the UPA/E8×E8 heterotic superstring, showing how YAH prescribes how many circularly polarised oscillations make up each revolution of these 10 whorls. Their five revolutions comprise (5×3360=16800) turns. The number 26 of YAHWEH is the dimensionality of the space-time of bosonic strings and the number 15 of YAH is the number of dimensions beyond the 11-d space-time predicted by M-theory, the yet-to-be discovered theory that encompasses both supergravity theory and the five superstring theories.

The superstring structural parameter 16800 can be represented by a five-pointed star, with each point corresponding to one of the 5 revolutions of the 10 whorls and consisting of a 15×15 array of the number 15 of YAH arranged in a parallelogram, the 1120 numbers outside the centre of the star adding up to 16800. The 600 15s in the red outer halves of the 5 points of the star add up to 9000 (=90×100). The 520 15s in the blue inner halves of the points add up to 7800 (=78×100). 78 is the gematria number value of Cholem and 90 is the number value of Yesodoth, the two words making up Cholem Yesodoth, the Kabbalistic name of the Mundane Chakra of Malkuth. The geometry of the 5-pointed representation of the superstring structural parameter 16800 naturally distinguishes between the gematria number values of these words. The UPA is par excellence the micro-physical manifestation of the Mundane Chakra of Malkuth.
.png)




