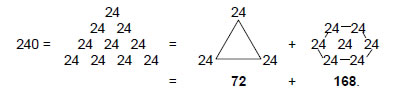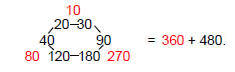ARTICLE 30
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
|
Earlier analysis of the Archimedean and Catalan solids constructed from the tetractys — the template of straight-line, sacred geometry — revealed that the disdyakis triacontahedron (the Catalan solid with the most vertices) embodies the structural parameter 1680 of the E8×E8 heterotic superstring. This article completes the analysis by proving that this polyhedron also embodies its structural parameter 840. The triakis tetrahedron (the simplest Catalan solid) and the disdyakis triacontahedron are the polyhedral version of Plato’s Lambda Tetractys, whose numbers generate the tone ratios of the notes of the Pythagorean musical scale. The 120 faces of the disdyakis triacontahedron contain 480 hexagonal yods. They symbolize the 480 roots of E8×E8 and are the counterparts of the 480 hexagonal yods of the two similar sets of seven regular polygons that constitute the inner form of the Tree of Life. The direct product nature of this gauge symmetry group reflects the fact that each face and vertex of the disdyakis triacontahedron has a mirror image. |
In previous articles, it was proved that, when each of the 120 triangular faces of the disdyakis triacontahedron (Fig. 1) is constructed from three tetractyses and the triangles in its interior are turned into single tetractyses (case C), there are 1320 geometrical elements surrounding its axis. When its faces are single tetractyses and the interior triangles are divided into three tetractyses (case A), there are 1680 elements surrounding its axis. When its faces are each divided into three tetractyses and its internal triangles are divided into three triangles (case B), there are 2400 elements surrounding its axis. In this article, we shall consider the final possibility (case D), wherein internal triangles and faces are single tetractyses. Of the four possible cases, only cases B and C have counterpart transformations in the Archimedean and Catalan solids because consistency of construction requires a face that is a regular polygon with n sides to be divided into n triangular sectors.
1
Cases A and D are exceptions to the general rule of construction of polyhedra from tetractyses. This does not mean, however, that they lack legitimacy or significance. On the contrary, the disdyakis triacontahedron in case A embodies the
superstring structural parameter 1680 and (as we shall see shortly) provides another such parameter in case D. What it does mean is that polyhedra like the disdyakis triacontahedron with only triangular faces are a special case because their faces can be constructed from tetractyses in two ways, not one, i.e., from one or three tetractyses. As none of the Archimedean solids has only triangular faces, only the Catalan solids need to be considered in case D. As in earlier articles, we shall consider an axis passing through two diametrically opposite vertices of a polyhedron and then calculate the number of geometrical elements and the number of yods that surround this axis, simplifying expressions by using Euler’s equation for a polyhedron:
C – E + F = 2.
The central axis passing through two such vertices consists of three corners of tetractyses (two polyhedral vertices and its centre) and two edges of tetractyses (Fig. 2). Seven yods lie on the axis (three corners and four hexagonal yods).
For case D:
Number of vertices ≡ V = C + 1. Number of vertices surrounding axis ≡ V' = V – 3 = C – 2 = E – F.
Number of edges ≡ e = C + E. Number of edges surrounding axis ≡ e' = C + E – 2.
Number of triangles ≡ T = E + F. Number of triangles surrounding axis = E + F.
Total number of geometrical elements ≡ N = 2C + 2E + F + 1 = C + 3E + 3.
Number of geometrical elements surrounding axis ≡ N' = C + 3E – 2.Table 1. Numbers of geometrical elements in the Catalan solids (case D).
triakis tetrahedron rhombic dodecahedron triakis octahedron tetrakis hexahedron deltoidal icositetrahedron pentagonal icositetrahedron rhombic triacontahedron disdyakis dodecahedron triakis icosahedron pentakis dodecahedron deltoidal hexacontahedron pentagonal hexacontahedron disdyakis triacontahedron According to Table 1, the triakis tetrahedron — the Catalan solid with fewest vertices — consists of 60 vertices, edges and triangles surrounding its axis. The disdyakis triacontahedron — the Catalan solid with most vertices — consists of 600 geometrical
2
elements surrounding its axis. Indeed, for the latter, the numbers of vertices (V'), edges (e') and triangles (T) surrounding its axis are ten times the corresponding numbers for the former. The Godname ADONAI with number value 65 is assigned to Malkuth.1 It prescribes the triakis tetrahedron because the simplest Catalan solid comprises 65 vertices, edges and triangles. It has 36 vertices and triangles, where 36 is the number value of ELOHA, Godname of Geburah. The Godname EHYEH with number value 21 assigned to the Sephirah Kether prescribes this
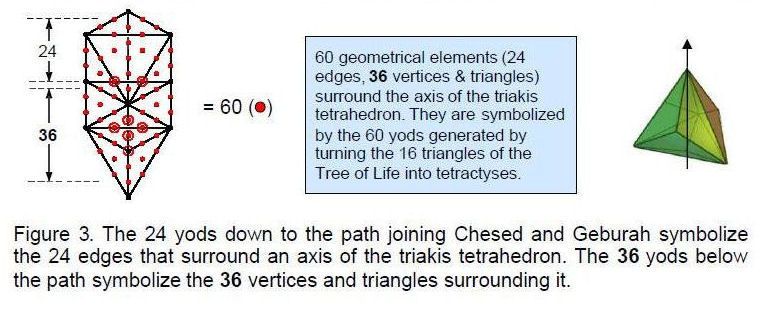
polyhedron because, counting firstly the five Platonic solids, then the 15 Archimedean solids and, finally, the Catalan solids, the triakis tetrahedron is the 21st polyhedron. The Godname YAHWEH with number value 26 assigned to Chokmah prescribes the triakis tetrahedron because its 18 tetractyses have 26 edges. Two edges form its axis, so that 24 edges surround it. The 60 geometrical elements surrounding the axis comprise 24 edges and 36 vertices and triangles.
The counterpart of this in the Tree of Life is the fact that, constructed from 16 tetractyses, it has 60 yods other than the ten Sephiroth at their corners (Fig. 3). Each yod symbolizes one of the geometrical elements in the triakis tetrahedron. The 24 yods below the apex of the Tree of Life down to the path connecting Chesed and Geburah denote the 24 edges around the axis and the 36 yods below the path denote the 36 vertices and triangles that surround it. This is striking evidence that the triakis tetrahedron is the polyhedral counterpart of the outer form of the Tree of Life.
The numbers of yods in the faces and in the interiors of a polyhedron with triangular faces are calculated below:
Faces
Number of corners of tetractyses = C. Number of corners surrounding axis = C – 2 = E – F.
Number of hexagonal yods on edges of tetractyses = 2E.
Number of hexagonal yods at centres of tetractyses = F.
Total number of hexagonal yods ≡ Hs = 2E + F.
Number of yods surrounding axis ≡ Ns = C – 2 + Hs = C – 2 + 2E + F = 3E.Interior
Number of corners of tetractyses = 1 (centre of polyhedron).
Number of hexagonal yods on edges of tetractyses ≡ 2C.
Number of hexagonal yods at centres of tetractyses = E.
Total number of hexagonal yods surrounding axis ≡ Hi = E + 2C – 4 = 3E – 2F.
Total number of yods surrounding axis ≡ Ni = Hi = 3E – 2F.3
4
Total number of corner yods surrounding axis ≡ C' = C – 2 = E – F.
Total number of hexagonal yods surrounding axis ≡ H = Hs + Hi = 5E – F.
Total number of yods surrounding axis ≡ N = C' + H = 6E – 2F.Table 2. Numbers of yods in the Catalan solids (case D).
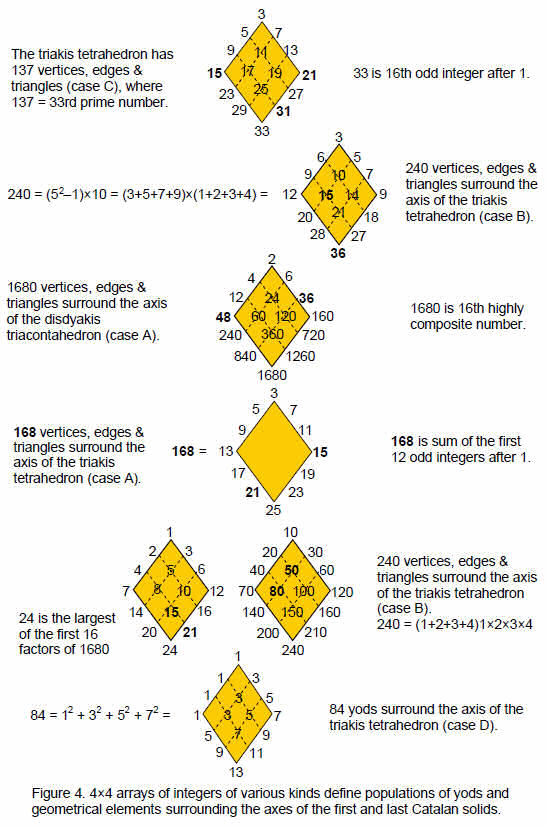
Catalan solid triakis tetrahedron rhombic dodecahedron triakis octahedron tetrakis hexahedron deltoidal icositetrahedron pentagonal icositetrahedron rhombic triacontahedron disdyakis dodecahedron triakis icosahedron pentakis dodecahedron deltoidal hexacontahedron pentagonal hexacontahedron disdyakis triacontahedron Table 2 lists the yod populations of those Catalan solids that have only triangular faces (other solids have cells with dashes). The triakis tetrahedron has 84 yods surrounding the seven yods along its axis, where
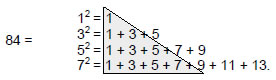
84 = 12 + 32 + 52 + 72.
This can be expressed as:
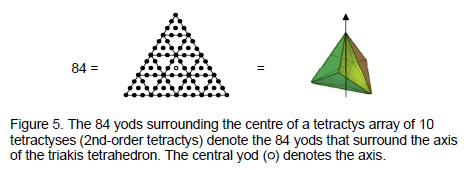
This provides a 4×4 array of odd integers adding to 84 (Fig. 4, bottom). The ten integers enclosed in the grey triangle form the upper half of the rhombic array shown in Fig. 4. The 2nd-order tetractys (Fig. 5) — the next higher order of differentiation of the (1st-order) tetractys — has 85
yods, 84 of them surrounding its centre. The 1, 2, 3 & 4 points in the four rows of the tetractys symbolise the sequence of generation of the tetrahedron from a mathematical point:
5
point
line
triangle
tetrahedron.
Its next higher-order version denotes the triakis tetrahedron, which is formed from the tetrahedron by raising the centres of its four faces (mathematicians call this process ‘cumulation’). The 2nd-order tetractys also symbolises the tetrahedron in case B because the latter consists of 15 vertices (symbolized by the 15 corners of the ten tetractyses), 40 edges and 30 triangles (symbolized by their 70 hexagonal yods), that is, 85 geometrical elements.2
The polyhedron has 91 yods, where
91 = 12 + 22 + 32 + 42 + 52 + 62,
and
12 = 1
22 = 1 + 3
32 = 1 + 3 + 5
42 = 1 + 3 + 5 + 7
52 = 1 + 3 + 5 + 7 + 9
62 = 1 + 3 + 5 + 7 + 9 + 11.The 21 odd integers adding to 91 demonstrate how the Godname EHYEH with number value 21 prescribes the yod population of the triakis tetrahedron. As 15 integers lie on the boundary of this triangular array, it also shows how the Godname YAH with number value 15 prescribes this number.
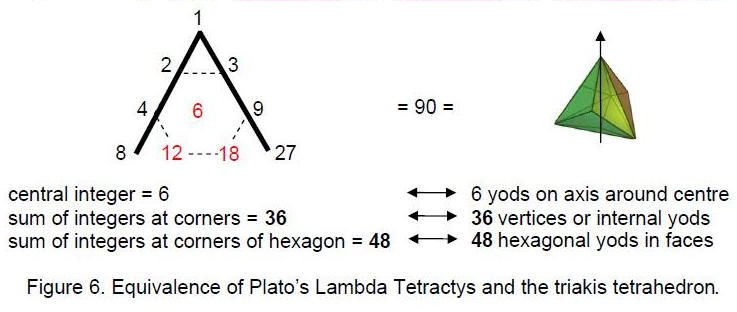
Starting from a point, 90 more yods are needed to construct the triakis tetrahedron from its 30 tetractyses. As discussed in Article 27,3 the Lambda array of powers of 2 and 3 made famous by Plato in Timaeus, his treatise on cosmology, is but seven of ten integers arranged in a tetractys (Fig. 6). Including the three interpolated integers (shown in red in Fig. 6), the ten integers add up to 90, which is the number of yod surrounding the centre of the triakis tetrahedron. The integer 6 at the centre of the tetractys corresponds to the number of yods on the axis of the polyhedron
that surround its centre. The sum (36) of the integers at the corners of the tetractys corresponds to the 30 internal yods and the six vertices surrounding the axis. The sum (48) of the six integers at the corners of a hexagon in the Lambda Tetractys corresponds to the 48 hexagonal yods in the faces of the polyhedron.
This correlation demonstrates that the Lambda Tetractys and the triakis tetrahedron are, respectively, the arithmetic and geometrical expressions of the same mathematical archetype. It manifests spiritually as the 90 subplanes of the seven cosmic planes
6
above the lowest subplane of the physical plane described by Theosophy.4 The seven yods on the axis symbolize the seven subplanes of the physical plane, the 42 yods on the 18 edges symbolize the 42 subplanes of the six planes of the cosmic physical plane above the physical plane and the 42 yods either inside the polyhedron or at the centres of the 12 faces symbolize the 42 subplanes of the six superphysical, cosmic planes. The three yods on the axis that are corners of tetractyses denote what Theosophy calls the three ‘dense physical subplanes’ and the four hexagonal yods on the axis denote the four etheric subplanes. The correlation between the Lambda Tetractys and the triakis tetrahedron manifests physically as the (10×9=90) coordinate variables needed to track the motion of the ten closed curves in 10-dimensional space-time that constitute the heterotic superstring constituent of quarks. Notice in both cases that the total number of degrees of freedom — subplanes or space-time coordinates of the curves — is 91, which is the number of yods in the triakis tetrahedron. The reason for this is that the seven planes and the heterotic superstring are, respectively, the macrocosmic and microscopic manifestations of the Tree of Life blueprint.5
The Lambda Tetractys generates the tone ratios of the notes of the Pythagorean musical scale as ratios of pairs of integers.6 The sums 36 and 54 of, respectively, the integers at its three corners and the integers at the centre and corners of a hexagon also define the perfect fifth with tone ratio 3/2 because 54/36 = 3/2, whilst the sums 36 and 48 define the perfect fourth with tone ratio 4/3 because 48/36 = 4/3. The triakis tetrahedron also defines the perfect fifth because its faces and interior have, respectively, 36 and 24 geometrical elements surrounding its axis, and 36/24 = 3/2.
For case D, according to Tables 1 and 2, every number of yods or geometrical elements surrounding the axis of the disdyakis triacontahedron is ten times its counterpart in the triakis tetrahedron. Surrounding its axis are 600 geometrical elements and 840 yods. Among the latter are 60 vertices and (180×2=360) hexagonal yods on its edges, that is, (360+60=420) yods form its edges, leaving 420 yods either at centres of faces or inside the polyhedron. As
292 – 1 = 840 = 3 + 5 + 7 + … + 57,
840 is the sum of the first 28 odd integers after 1. The number 29 is the largest of the first ten prime numbers:
2
3 5
7 11 13
17 19 23 29 .The number (120) of faces of the disdyakis triacontahedron is the sum of the first ten odd integers after 1:
3
5 7
120 = 9 11 13
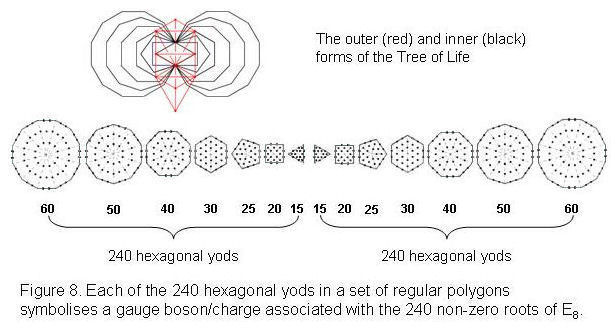
15 17 19 21 .As the largest of these integers, the number value 21 of EHYEH, Godname of Kether, determines the number of faces of this Catalan solid. These faces contain 480 hexagonal yods (see the value of Hs for the disdyakis triacontahedron in Table 2). This is also the number of hexagonal yods in the 32 faces of the icosahedron and the dodecahedron when they are constructed from tetractyses, as well as the number of hexagonal yods in the 38 faces of the tetrahedron, octahedron, cube and icosahedron
7
that the ancient Greeks believed were the shapes of the particles of the elements Fire, Air, Earth and Water.7 The superstring gauge symmetry group E8×E8 has 480 non-zero roots (240 for each E8). This group-theoretical parameter of superstrings is therefore embodied in the disdyakis triacontahedron as the number of hexagonal yods creating its outer form. In other words, the polyhedral form of the Tree of Life is associated with the 480 gauge bosons corresponding to these roots. The direct product structure of the E8×E8 heterotic superstring gauge symmetry group
arises from the inversion symmetry (Fig. 7) of the polyhedral Tree of Life because 60 faces contain 240 hexagonal yods and their 60 mirror images contain 240 hexagonal yods as well.
The counterpart of this mirror symmetry in the polygonal, inner form of the Tree of Life is its two sets of seven regular polygons, one being the mirror image of the other (Fig. 8).
8
yods. A yod denotes a gauge boson and gauge charge associated with those generators of the Lie algebra of E8 that are defined by its 240 roots. As with the disdyakis triacontahedron, the fact that one set of polygons is the mirror image of the other explains why the gauge symmetry group of this superstring is the direct product of two identical groups E8.
As
48 = 72 – 1 = 3 + 5 + 7 + 9 + 11 + 13
and
10 = 1 + 2 + 3 + 4,
480 = 48×10 = (3+5+7+9+11+13)×(1+2+3+4).
As
24 = 52 – 1 = 3 + 5 + 7 + 9,
240 = 24×10 = (3+5+7+9)×(1+2+3+4).Therefore,
480 – 240 = 240 = (11+13)×(1+2+3+4)
= (11+13+22+26) + (33+39+44+52)
= 72 + 168,where 72 is the sum of the four smallest integers and 168 is the sum of the four largest integers. This division is therefore determined by the Tetrad (4).
The same 72:168 division of 240 was found in Article 278 to appear in the triakis tetrahedron. In case A, 168 vertices, edges & triangles surround its axis and in case B, 240 such geometrical elements surround its axis, that is, 72 elements are added by the construction of each of the 12 faces into three tetractyses. In terms of a tetractys array of the integer 24:
9
the transformation amounts to considering a whole tetractys array instead of just a hexagon. In terms of the equivalence between the Tree of Life and tetractys, this means that all ten Sephiroth are considered instead of just the seven Sephiroth of Construction. In terms of the root structure of E8, the 72:168 division denotes the 168 roots of E8 that are not also roots of its exceptional subgroup E6, which has 72 roots.9
Fig. 9 depicts the UPA (‘ultimate physical atom’), the fundamental unit of matter described by Annie Besant & C.W. Leadbeater. Identified by the author as the E8×E8 heterotic superstring constituent of quarks, this object consists of ten closed curves, or ‘whorls.’ In the ‘positive’ type of UPA, the whorls wind clockwise around the axis when viewed from the top. In the ‘negative’ variety, they wind anticlockwise. Fig. 9 shows a positive type of UPA. The uppermost three whorls, called ‘major whorls,’ are different from the seven others (called ‘minor whorls’) in ways that need not be discussed here. The 3:7 division between these two types of whorls is the manifestation of the ontological distinction in the Tree of Life map of all beings between the Supernal Triad of Kether, Chokmah and Binah and the seven Sephiroth of Construction. In the context of the tetractys, wherein each yod symbolises a whorl, the major whorls correspond to the yods at the corners of the tetractys and the seven minor whorls correspond to the seven yods at the corners and centre of a hexagon. According to the author’s research, 24 gauge charges of E8 are spread along each curve. This means that the three major whorls carry 72 charges of E8 and the seven minor whorls carry 168 charges. This is the superstring counterpart of the 168 geometrical elements surrounding the axis of the triakis tetrahedron in case A and the extra 72 elements added to its faces in case B. The 240 geometrical elements that surround the axis of this polyhedron in the latter case represent degrees of freedom whose counterparts in the E8×E8 heterotic superstring are its 240 E8 gauge charges.
Each whorl is a helix with 1680 turns. It is a standing wave with 1680 circularly polarised oscillations. This is the string manifestation of the 1680 vertices, edges and triangles surrounding the axis of the disdyakis triacontahedron in case A. Figure 8 shows that a whorl makes five revolutions around its axis. It winds 2½ times in an outer spiral, making 840 oscillations, and 2½ times in a narrower spiral, making another 840 oscillations. Alternatively, there are 840 turns in a half-revolution of five whorls. This is the string manifestation of the 840 yods surrounding the axis of the disdyakis triacontahedron in case D (see Table 2). There are 168 turns in a half-revolution of a whorl and 84 turns in a quarter-revolution. This is the string manifestation of the 84 yods surrounding the axis of the triakis tetrahedron. The ten-fold difference between the populations of yods or geometrical elements in the first and last Catalan solids has its counterpart in the heterotic superstring as the ten half-revolutions of each whorl and as the ten quarter-revolutions in the inner or outer half of a whorl. The disdyakis triacontahedron embodies the number of oscillations in each whorl of the superstring made during 2½ revolutions (case D) and five revolutions (case A).
According to Table 2, the 840 yods surrounding the axis of the disdyakis triacontahedron consist of the 480 hexagonal yods in its 120 faces and 360 other yods (60 vertices and 300 hexagonal yods in its interior). Multiplying the Lambda Tetractys of integers by 10, the sum of the integers at its corners is 360 and the sum of the integers at the corners of a hexagon is 480:
10
Magnified by the Pythagorean factor of 10, the Lambda Tetractys is an arithmetic version of the disdyakis triacontahedron. The central integer 6 corresponds to the central axis. In the triakis tetrahedron, it denotes the six yods on the central axis on either side of the centre of the polyhedron. The sum of the seven integers at the centre and corners of a hexagon is 540. This is the number of yods on the sides of the 300 tetractyses needed to construct the polyhedron. The number defining the edges of these building blocks is determined aptly by the very numbers whose positions in a tetractys are occupied by yods that symbolize the seven Sephiroth of Construction.
The sum of the seven integers forming the Lambda modified by multiplying by 10 is 540. This is the number of yods on the 120 faces of the disdyakis triacontahedron:
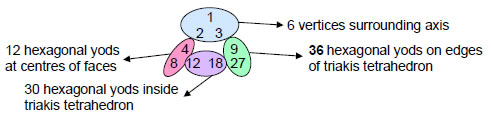
The two interpolated integers on the base of the Lambda Tetractys are 120 and 180. They denote, respectively, the number of hexagonal yods on the 60 edges of the 180 internal triangles (60×2=120) and the number of hexagonal yods at the centres of the latter. Combinations of the nine integers surrounding the centre of the Lambda Tetractys when multiplied by 10 therefore determine the numbers of various types of yods in the 300 tetractyses making up the disdyakis triacontahedron. As the latter numbers are ten times their counterparts in the triakis tetrahedron (see Table 2), this demonstrates the equivalence between the Lambda Tetractys and this Catalan solid:
The sum of the four integers 8, 12, 18 & 27 forming the base of the Lambda Tetractys is 65, which is the number value of ADONAI, the Godname of Malkuth. It is the number of vertices (9), edges (26) and triangles (30) in the triakis tetrahedron (see Table 1), showing how this Godname prescribes the simplest Catalan solid. The two integers 8 and 18 add up to 26, the number of edges, and the two other integers 12 and 27 add up to 39, which is the number of vertices and triangles. The geometrical properties of the triakis tetrahedron are therefore represented by groups of integers belonging to the Lambda Tetractys. The reason for this is simple: they are the arithmetic and polyhedral expressions of the archetypal blueprint of the Tree of Life, whose inner, polygonal form can be shown10 to encode its own 91-fold replication to generate the Tree of Life mapping of the 91 subplanes of the seven cosmic planes of consciousness. Article 1111 discussed the way in which the number 540 — the sum of the nine integers surrounding the centre of the modified Lambda Tetractys — expresses the number of emanations of the 90 trees down to the top of the lowest Tree of Life that map the seven planes. It is summarised here briefly: 91 overlapping Trees of Life have 550 emanations (see ref. 11). The lowest of these has 11 emanations. There are (550–11=539) emanations
11
12
above the top of the lowest tree, that is, 540 emanations down to Kether of the first tree. Just as the seven yods on the axis of the triakis tetrahedron surrounded by 84 yods symbolize the seven subplanes of the physical plane interpenetrated by 84 higher subplanes, so the 540 yods in the faces of the disdyakis triacontahedron that surround its axis symbolise the 540 emanations of the 90 trees extending down to the top of the lowest one. The latter represents the lowest subplane, which, being the seventh, bears a correspondence to the physical plane (the seventh plane). The numbers 84 and 540 express the same kind of information — the former as trees and the latter as their emanations. 539 is the sum of the number values of the Godnames assigned to the seven Sephiroth of Construction:
539 = 31 + 36 + 76 + 129 + 153 + 49 + 65
(see table in Ref. 1). This is not coincidental but, instead, an example of the remarkable, designing potency of the Godnames.
The sum of the four integers forming the base of the Lambda Tetractys multiplied by 10 is 650. This is the number of yods in the 144 faces of the 144 Polyhedron when they are constructed from tetractyses, showing how ADONAI, the Godname of Malkuth with number value 65, prescribes
the polyhedron that — together with the disdyakis triacontahedron — constitute what was called in Article 2312 the ‘polyhedral Tree of Life.’ The number 650 is the sum of the Godname numbers of the first four Sephiroth:
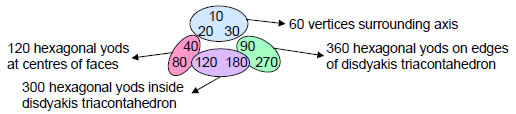
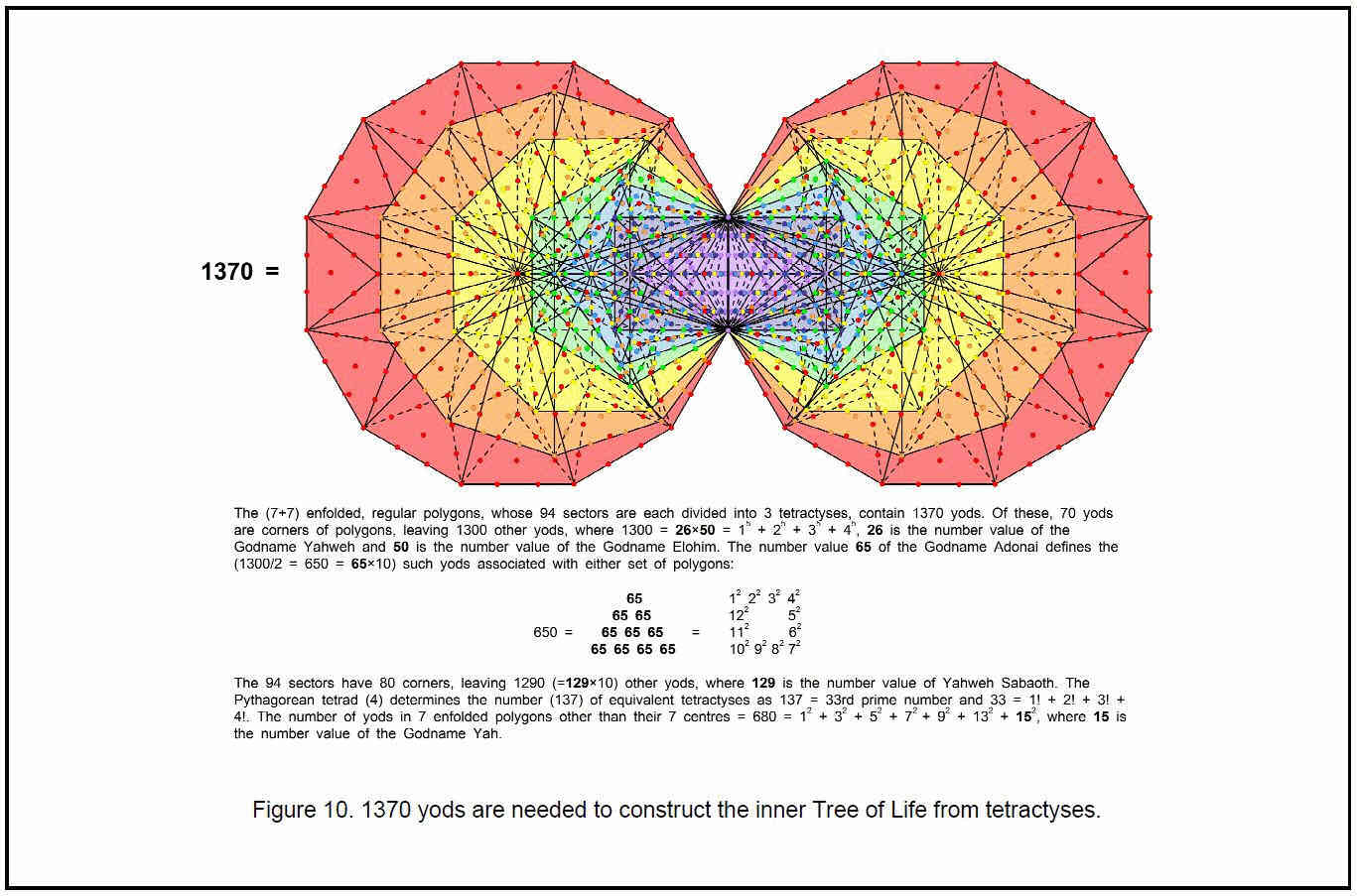
650 = 543 + 26 + 50 + 31.
It is also the number of yods other than corners associated with each set of seven enfolded polygons when each of their 94 sectors is divided into three tetractyses (Fig. 10). In other words, it is the number of extra yods needed to construct each half of the inner Tree of Life — its actual form, in keeping with the meaning of Malkuth.
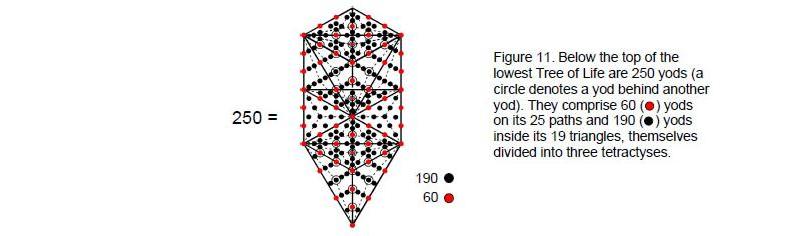
The sum of the six integers above the base of the Lambda tetractys is 250. It is the sum of the central integer 60 and the five integers on its sides that add to 190:
13
The significance of this is that the lowest of the 91 overlapping Trees of Life mapping the spiritual cosmos has 250 yods below its apex when each of its 19 triangles is divided into three tetractyses (Fig. 11). Below this point, there are 60 yods on its 25 paths and 190 yods inside its triangles. As already pointed out, the apex is the 540th emanation, where 540 is the sum of the six integers at the corners of a hexagon that surround the central integer 60. The sum 250 is therefore the number of yods in the lowest Tree of Life below the 540th emanation. The lowest tree corresponds to Malkuth, so it is apt that the Godname ADONAI of this Sephirah of Construction has the very number value 65 that specifies the base of four integers and hence the six remaining integers of the Lambda Tetractys whose sum is the number of yods in this tree.
The significance of the number 250 for superstring physics is that ten independent, non-intersecting curves in 26-dimensional space-time need (10×25+1=251) rectangular space-time coordinate variables. They are symbolised by the 251 yods of the lowest Tree of Life. One variable is the time coordinate, symbolized by the apex of the tree. The 250 spatial coordinates of the ten curves are determined by the sum of the six integers in the Lambda Tetractys above its base specified by the Godname of Malkuth. This is truly a Malkuth level of description of the superstring as ten separate, closed curves in 26-dimensional space-time. Each curve is a whorl of the UPA described by Besant and Leadbeater (see Fig. 9). In terms of the disdyakis triacontahedron, the central integer 60 in the Lambda Tetractys corresponds in this particular context to the 60 vertices
Table 3. Number values of the Sephiroth in the four Worlds.
Sephirah
Angels
ChakraKether Chokmah Binah Chesed Geburah Tiphareth Netzach Hod Yesod Malkuth surrounding its axis (or, alternatively, to its 60 faces and their mirror images. They are symbolized in the lowest Tree of Life by the 60 yods below its apex that lie along its paths and thus create its shape. In this sense, Plato’s Lambda marks out uniquely the disdyakis triacontahedron, for it is the only Catalan solid that has 60 vertices and 840 yods surrounding its axis. As Table 1 shows, these 840 yods are associated with 600 vertices, edges and triangles — a further illustration of how the root number 6 at the centre of the original Lambda Tetractys determines the nature of the sacred geometry of the disdyakis triacontahedron. In music, it fixes the frequency, or pitch, of the starting note (tonic) of the musical scale as unity, so that the ratios of the other integers to 6 are the tone ratios of the notes. The integer 6 is the starting point for the Pythagorean musical scale, its diversification in the seven octave species, the Tree of Life counterpart of the Lambda Tetractys and its polyhedral equivalent — the triakis tetrahedron and the disdyakis triacontahedron.
14
References
1The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras. Table 3 above gives their number values calculated by the practice of gematria, wherein each letter of a word has a number assigned to it, giving a number value to the word that is the sum of the number values of its letters. Numbers from this table that are referred to in the article are written in boldface.2 Phillips, Stephen M. Article 27: “How the Disdyakis Triacontahedron Embodies the Structural Parameter 1680 of the E8×E8 Heterotic Superstring,” (WEB, PDF), pp. 2–3.5 Phillips, Stephen M. Article 5: “The Superstring As Microcosm of the Spiritual Macrocosm,” (WEB, PDF).6 Phillips, Stephen M. Article 11: “Plato’s Lambda — Its Meaning, Generalisation and Connection to the Tree of Life,” (WEB, PDF), pp. 2–3.9 Phillips, Stephen M. Article 22: “The Disdyakis Triacontahedron As the 3-dimensional Counterpart of the Inner Tree of Life,” (WEB, PDF), pp. 3–4.10 Phillips, Stephen M. “The Mathematical Connection between Religion and Science” (Antony Rowe Publishers, England, 2009).15