1. Embodiment of the division: 3840 = 1920 + 1920
in the inner form of 10 Trees of Life

48 corners and 96 sides of 48 triangular sectors surround the centres of the 7 separate Type A polygons. These 192 geometrical elements comprise 24 geometrical elements in the green hexagon, 84 elements in the blue triangle, octagon & decagon and 84 elements in the red square, pentagon & dodecagon. Each element has its mirror-image counterpart in the set of 7 polygons on the other side of the Tree of Life. (192+192=384) geometrical elements surround the centres of the (7+7) separate Type A polygons.

The inner form of 10 overlapping Trees of Life (or the 10-tree shown opposite) consists of (70+70) enfolded polygons. The centres of the 140 separate polygons are surrounded by 3840 geometrical elements. The 1920 geometrical elements surrounding the centres of the 70 separate polygons in each set comprise 240 elements in the 10 green hexagons, 840 elements in the blue triangles, octagons & decagons, and 840 elements in the red squares, pentagons & dodecagons. i.e.,

1920 = 240 + 1680,

where

1680 = 840 + 840.

This is the geometrical counterpart of the 1920 hexagonal yods that line the sectors of the 70 separate Type A polygons making up each half of the inner form of 10 Trees of Life. 240 such yods line the sectors of the 10 hexagons and the remaining 1680 yods line the sectors of the 60 other polygons. 840 hexagonal yods line the sectors of the triangles, octagons & decagons and 840 hexagonal yods line the sectors of the squares, pentagons & dodecagons.

There is no alternative to associating the number 240 in the equation above uniquely to the hexagon because:

1. no other subset of the set of 7 polygons has 6 sectors; 
2. the 1920 geometrical elements surrounding the centres of the 70 polygons consist of 480 corners, 480 sides of polygons, 480 internal sides of sectors & 480 triangles, so that the number 240 refers only to the number of geometrical elements of each type making up the 35 polygons associated with 5, not 10, Trees of Life. 

However, the triangle, square & pentagon have 24 corners & sides, as do either the dodecagon or the square & octagon. In each case, this means that the 10 sets of 7 polygons have 240 corners & sides, 840 corners & triangles and 840 external and internal sides. Therefore, they display the holistic division:

1920 = 240 + 840 + 840

in several ways. Rather than pose a problem, this lack of uniqueness confirms that the existence of the division is not a coincidence.

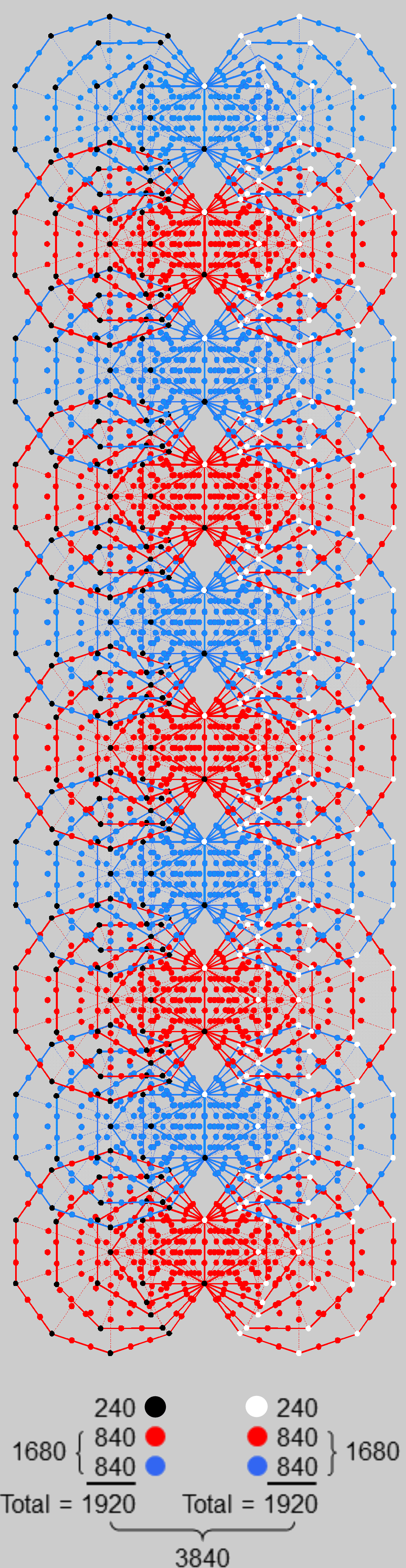
The 1st (6+6) polygons in the inner
form of 10 Trees of Life have
(1920+1920=3840) yods that are
intrinsic to these polygons (notice
that no black or white yod is assigned
to the topmost corners of the hexagons
enfolded in the highest Tree of Life.
This is because these two corners are
not intrinsic to the polygons enfolded in
the 10 Trees, being also the corners of
the two hexagons (not shown) enfolded

in the 11th Tree of Tree.

A superstring interpretation of the 3840 yods

The rank-8 exceptional Lie group E₈ has 240 non-zero roots. They include the 12 roots of G₂, the 48 roots of F₄, the 72 roots of E₆ and the 126 roots of E₇, where G₂≤F₄≤E₆≤E₇≤E₈. There are (240−72=168) roots of E₈ that are not roots of E₆ and (240−48=192) roots of E₈ that are not roots of F₄. As E₆ has (72−48=24) roots that are not roots of F₄, the 192 roots comprise these 24 roots and the 168 roots:

192 = 24 + 168.

The 192 yods associated with each set of 6 enfolded polygons denote the 192 roots of E₈ that are not roots of F₄, whilst the 24 corners denote the 24 roots of E₆ that are not roots of F₄ and the remaining 168 yods denote the 168 roots of E₈ that are not roots of E₆. Each root is associated with a generator of the symmetry group E₈, which in turn defines a gauge charge and the 10-dimensional vector gauge field that couples to it. If each of the 10 dimensions of superstring space-time are mapped by a Tree of Life, there are (1920+1920=3840) yods that are intrinsic to the (60+60=120) polygons enfolded in the inner form of 10 Trees of Life that map superstring space-time. Each set of 1920 yods consists of 240 corners of 60 polygons and their 1680 yods. The former denote the 240 space-time components of the 24 gauge fields associated with the gauge charges corresponding to the 24 roots of E₆ that are not roots of F₄; the latter denote the 1680 components of the 168 gauge fields associated with the gauge charges that correspond to the 168 roots of E₈ that are not roots of E₆ (and, therefore, its exceptional subgroup F₄).

This interpretation of the holistic pattern displayed by the first 6 polygons in the inner form of 10 Trees of Life:

3840 = 1920 + 1920

implies that the symmetry group for superstrings is E₈×E₈, i.e., that the type of superstring is the E₈×E₈ heterotic superstring.

2. The first 6 types of polygons enfolded in the inner
form of 10 Trees of Life have (3840=1920+1920) yods

The first 6 enfolded polygons are the triangle, square, pentagon, hexagon, octagon & decagon. Separately, they have 36 corners; enfolded, they have 26 corners, of which 21 are outside the root edge and unshared with the outer Tree of Life. The first (6+6) enfolded polygons have 50 corners. This is how the Godnames EHYEH with number value 21, YAHWEH with number value 26, ELOHIM with number value 50 and ELOHA with number value 36 prescribe this subset of the 7 polygons making up the inner form of the Tree of Life. The number of yods in a Type A n-gon = 6n +1. The number of yods in the first 6 separate polygons = ∑(6n+1) = 6×36 + 6 = 222. When they are enfolded, the corner of the pentagon coincides with the centre of the decagon and the triangle overlaps a sector of the hexagon, causing 6 yods to disappear; (5×4=20) yods on the sides of 5 of the 6 polygons that coincide with the shared root edge when they are enfolded, likewise, disappear. The number of yods in the first 6 enfolded polygons = 222 − 1 − 6 − 20 = 195. They comprise 26 corners of polygons and 169 other yods. The number of yods in the first (6+6) enfolded polygons = 386. They include the topmost corners of the two hexagons, which coincide with the lowest corners of the two hexagons enfolded in the next higher Tree of Life. Therefore, 194 yods are intrinsic to the first 6 enfolded polygons and (386−2=384) yods are intrinsic to the first (6+6) polygons enfolded in each successive Tree because they are not shared with the polygons enfolded in the next higher Tree. They include (50−2=48) corners and (384−48=336) other yods. Associated with either set of the first 6 enfolded polygons are (384/2=192) such yods; they include (48/2=24) corners and (336/2=168) other yods. The divisions:

384 = 192 + 192,
192 = 24 + 168,

characterise all holistic systems (see The holistic pattern). This indicates that the subset of the complete set of 7 regular polygons that consists of their first 6 types constitutes a holistic system in itself.

The 10 sets of (6+6=12) polygons of the first 6 types that are enfolded in the inner form of 10 overlapping Trees of Life consist of 3840 yods that are intrinsic to these polygons. 1920 yods are associated with each set of 60 polygons. As there are (24+24) corners and (168+168) other yods per set of (6+6) enfolded polygons, the 1920 yods comprise 240 corners of polygons (coloured black on the left and white on the right in the diagram opposite) and 840 red yods and 840 blue yods in alternate sets of 6 polygons). These 1680 red & blue yods fill up the body of each set of 60 polygons whose shapes are marked out by their 240 corners. The 5:5 division in the 10 Trees generates the division: 1680 = 840 + 840. It manifests in the UPA (the subquark state of the E₈×E₈ heterotic superstring described paranormally by C.W. Leadbeater (see here) as the 840 1st-order spirillae in each outer or inner quarter-revolution of all 10 whorls, each one making 10 half-revolutions around its axis of spin (5 half-revolutions in its outer spiral from its apex to its nadir and 5 half-revolutions in its inner, narrower spiral). Each Tree maps a half-revolution of each whorl, 5 Trees representing the outer section of a whorl and 5 Trees representing its inner section. Yods in sets of polygons enfolded in successive Trees are shown as alternating in the colours red and blue in order to distinguish them.

3. Inner form of the Tree of Life with 4th-order polygons has (3840=1920+1920) sides

According to Table 9 on #45 of Sacred geometry/Tree of Life, the number of sides of the triangles making up the 7 enfolded, nth-order polygons = ½(35 + 47×3ⁿ). The triangles in the 7 4th-order polygons have 1921 sides (1920 outside the root edge). The (7+7) enfolded, 4th-order polygons have 2538 triangles with 3841 sides. This is the sum of the 91 squares of the numbers 1-10 forming a 10-fold array, showing how the Decad determines the number of sides of triangles forming the inner Tree of Life. The central square 12 corresponds to the root edge. Outside the root edge are 3840 sides. In each set of 7 enfolded polygons are 1920 sides. According to Table 1 of Properties of the polygons/Collective properties, the number of sides in the 3^n-1N triangles making up an nth-order N-gon = ½(3ⁿ+1)N. The 1st-order triangle contains 6 sides, the 4th-order triangle contains 123 sides & the 4th-order hexagon contains 246 sides. Therefore, the lattermost contains (246−6=240) sides other than the 3 sides of one sector of the hexagon occupied by the 4th-order triangle in the set of 7 enfolded polygons and the 3 sides of its own red, green & blue sectors. Being a 3rd-order triangle, each sector of the 4th-order hexagon contains 42 sides (41 outside the root edge). Therefore, the 4th-order triangle contains (123−42=81) extra sides. If the hexagon is regarded as containing 240 sides, the 4th-order triangle has (81+5=86) sides in the enfolded state (outside the root edge in both cases). The 6 enfolded, Type D polygons other than the hexagon contain 1680 sides. The numbers of sides in the 7 polygons outside the root edge are:

The triangle, square, pentagon & octagon contain 780 (=78×10) sides and the decagon & dodecagon contain 900 (=90×10) sides. This reproduces the respective gematria number values of Cholem (78) and Yesodoth (90), the two Hebrew words that make up the Kabbalistic name of the Mundane Chakra of Malkuth, which has number value 168.

.

4. 1920 yods line axes & tetractyses in the faces of the 5 Platonic solids

The 5 Platonic solids have 50 vertices, 50 faces and 90 edges. Their faces can be divided into 180 sectors. When these sectors are Type A triangles, i.e., when their faces are regular Type B polygons, the number of corners of tetractyses in the faces of the 5 Platonic solids = 50 +  50 + 180 = 280. This is the number value of Sandalphon, the Archangel of Malkuth. Inside each sector are three sides of tetractyses. The number of sides of the (3×180=540) tetractyses in all the faces = 90 + 180 + 3×180 = 810. The number of hexagonal yods lining these sides = 2×810 = 1620. The number of yods lining them = 280 + 1620 = 1900. This is 10 × the sum of the first 19 integers, where 19 is the 10th odd integer, showing how the Decad arithmetically determines the number of yods that line all the tetractyses needed to construct the faces of the 5 Platonic solids from Type A triangles. Each edge is the base of an internal triangle created by joining the two vertices at its end to the centre of the Platonic solid. This triangle, too, has three sectors that, for the sake of consistency, must be regarded as Type A triangles. The straight line passing through any two diametrically opposite vertices and the centre of a Platonic solid serves as its axis (in the case of the tetrahedron, which is the only Platonic solid that is not mapped to itself by point inversion, the axis is no longer straight because the tetrahedron lacks central symmetry, i.e., it does not have point symmetry). The axis of a Platonic solid is formed by two sides of two internal triangles, so that two hexagonal yods lie on each side when the triangles are Type A. The axes of the 5 Platonic solids are lined by (5×4=20) hexagonal yods. Therefore, (20+1900=1920) yods line these axes and all sides of the 540 tetractyses in the 50 Type B polygonal faces.

Of the 280 corners of tetractyses in the faces, 40 are vertices surrounding pairs of vertices that lie on the axes. Therefore, (280−40=240) corners are not vertices that shape the 5 Platonic solids. They comprise 10 vertices on axes, 50 centres of faces & 180 corners inside sectors of faces. There are (1920−240=1680) yods left that consist of the 40 vertices, the 20 hexagonal yods lining axes and the 1620 hexagonal yods lining sides of tetractyses. Therefore,

1920 = 240 + 1680.

On average, the axis and tetractyses in the faces of half a Platonic sold are lined by 192 yods other than its centre. They comprise 24 corners of 54 tetractyses that are not vertices surrounding its axis and 168 other yods. On average, a Platonic solid has (192+192=384) yods lining its axis and the 108 tetractyses in its faces. They comprise 48 corners of 108 tetractyses that are not vertices surrounding its axis and 336 other yods, where:

384 = 192 + 192 = 48 + 336,

192 = 24 + 168,

48 = 24 + 24,

336 = 168 + 168  .

Including its centre, the average number of yods lining theaxis and tetractyses in a Platonic solid = 385 = 1² + 2² + 3² + 4² + 5² + 6² + 7² + 8² + 9² + 10².

5. The disdyakis triacontahedron fits 29 polyhedra with
(3840=1920+1920) hexagonal yods in their faces

Article 3 shows that, when their faces are Type A polygons, the tetrahedron has48 hexagonal yods, the octahedron and the cube each has 96 hexagonal yods, and the icosahedron and the dodecahedron each has 240 hexagonal yods (see also #2 inSuperstrings as sacred geometry/Platonic solids).

The 62 vertices of the disdyakis triacontahedron can accommodate 10 tetrahedra, 5 octahedra, 5 cubes, an icosahedron, one dodecahedron, 5 rhombic dodecahedra, a rhombic triacontahedron and an icosidodecahedron (the dual of the lattermost) — see pages 5, 6, 7 & 9 at Superstrings as sacred geometry/Disdyakis triacontahedron. When their faces are divided into their sectors and each sector turned into a tetractys, i.e., the faces are regarded as Type A polygons, the 21 Platonic solids other than the dodecahedron contain 1680 hexagonal yods. The letter values of EHYEH, the Godname of Kether with number value 21, denote the numbers of each type of Platonic solid:

AHIH = 21
A = 1 → one icosahedron;
H = 5 → 5 cubes;
I = 10 → 10 tetrahedron;
H = 5 → 5 octahedra.

The dodecahedron, the rhombic dodecahedra and the rhombic triacontahedron also have 1680 hexagonal yods, whilst the icosidodecahedron has 480 hexagonal yods. The faces of the 29 polyhedra have 3840 hexagonal yods, which divide into the 480 hexagonal yods of the icosidodecahedron and the 3360 hexagonal yods of the other 28 polyhedra:

3840 = 480 + 3360.

There are 1920 hexagonal yods in one set of halves of the 29 polyhedra and 1920 hexagonal yods in their other halves. They comprise 240 hexagonal yods in each half of the icosidodecahedron and 1680 hexagonal yods in each set of halves of the other 28 polyhedra. The reason why the number 480 should be associated with the icosidodecahedron rather than with its dual, the rhombic triacontahedron, which also has 480 hexagonal yods, is not merely that it is the only Archimedean solid amongst the 29 polyhedra. The more persuasive, arithmetic reason is that the set of polyhedra containing 1680 hexagonal yods must include either the icosahedron or the dodecahedron with 240 hexagonal yods because each of the other polyhedra contains 480 hexagonal yods and 480 is not a factor of 1680. Therefore, even though 1920 hexagonal yods are in the 22 Platonic solids that can be fitted in the disdyakis triacontahedron and 1920 hexagonal yods are in the Archimedean & Catalan solids, this assignment cannot generate the required division: 1920 = 240 + 1680, leaving the assignment discussed above as the only possible one.

6. The 3-d Sri Yantra embodies the division: 1920 = 240 + 1680

The 3-d Sri Yantra consists of 42 triangles with 84 corners and 126 sides that surround a central triangle, above which is a single point, or bindu (). When each triangle is Type B, it has 46 yods (7 corners & 39 hexagonal yods in 9 tetractyses). 30 hexagonal yods () line their 15 sides (12 internal).

The number of external corners of the 42 Type B triangles = 2×42 = 84.
The number of their internal corners = 42×4 = 168.
Total number of corners = 84 + 168 = 252.
Number of their internal sides = 42×12 = 504.
Total number of sides = 126 + 504 = 630.
Number of hexagonal yods lining sides = 2×630 = 1260.
Number of hexagonal yods at centres of (42×9=378) tetractyses = 378.
Total number of hexagonal yods = 1260 + 378 = 1638.
Number of yods in 42 triangles = 252 + 1638 = 1890.
Number of yods in 43 triangles other than 16 corners & centres of 9 tetractyses in central triangle = 30 + 1890 = 1920 = 5×(2² + 3² + 4² + 5² + 6² + 7² + 8² + 9² + 10²).

Including the bindu and the 16 corners & centres, the total number of yods = 1 + 16 + 1920 = 1937. This number can be represented by a 5-fold array of the squares 1²-10² enclosed by a square array of the number 4. The 46 squares add up to 1921, which is the number of yods (including the bindu but excluding the 16 corners & centres) in the 3-d Sri Yantra whose 43 triangles are Type B triangles with 46 yods. There are (4+46=50) numbers in the representation of the total yod population 1937. This shows how ELOHIM with number value 50 prescribes the 3-d Sri Yantra.

The 7 corners of the 9 tetractyses in each Type B triangle comprise its unshared point (), the two corners () shared with adjacent triangles in its own layer (one per triangle) and 4 internal corners (). The 42 Type B triangles have (42×9=378) tetractyses with 42 shared corners and (42×5=210) unshared corners that comprise 42 unshared points and (42×4=168) internal corners. There are (30+210=240) yods other than shared corners that are either hexagonal yods () lining sides of the central triangle, unshared points () or corners () inside the 42 triangles:

240 = 30 () + 42 () + 168 () = 72 (,) + 168 ().

These 240 yods symbolise the 240 roots of the rank-8 exceptional Lie group E₈ that appears in E₈×E₈ heterotic superstring theory. The 72 yods correspond to the72 roots of its exceptional subgroup E₆ and the 168 yods correspond to the remaining 168 root of E₈. They comprise 24 hexagonal yods inside the central triangle, 6 hexagonal yods on its sides and 42 points, i.e., 48 yods; they denote the 48 roots of F₄, an exceptional subgroup of E₆. The number of hexagonal yods () and shared corners () in the 42 triangles = 1890 − 210 = 1680. Therefore,

1920 = 240 + 1680.

Apart from the Pythagorean factor of 10, this is the pattern that is characteristic of holistic systems (see The holistic pattern). The number 1680 is the number of circular turns in a helical whorl of the UPA, the subquark state of the E₈×E₈ heterotic superstring, as counted by C.W. Leadbeater, using micro-psi vision (see #11 of Occult Chemistry).

7. The 4₂₁ polytope embodies the division: 1920 = 240 + 1680

The 4₂₁ polytope (see here) embodies the division:

1920 = 240 + 1680.

E₈×E₈ conforms to the 192:192 division of 384 characteristic of holistic systems because its (240+240) roots are mapped by two 4₂₁ polytopes whose (240+240) vertices have 8-d position vectors with (1920+1920=3840) Cartesian coordinates. These correspond to the (1920+1920=3840) sides of the 2538 triangles in the inner Tree of Life with 4th-order polygons (see diagram #3).

Surrounding the centre of an n-gon divided into its sectors are n corners, n sides, n internal sides & n triangles, i.e., 4n geometrical elements. The 7 types of separate polygons of the inner form of the Tree of Life have (4×48=192) geometrical elements surrounding their centres. The hexagon (n=6) has 24 geometrical elements surrounding its centre. The square, pentagon & dodecagon have 21 corners with (4×21=84) geometrical elements surrounding their centres, as do the triangle, octagon & decagon. (192×10=1920) geometrical elements surround the centres of the 70 separate polygons making up the inner form of 10 Trees of Life. They comprise (24×10=240) corners of hexagons, 840 corners of squares, pentagons & dodecagons and 840 corners of triangles, octagons & decagons. (1920+1920=3840) geometrical elements surround the centres of both sets of 70 polygons, where

3840 = 240 + 240 + 1680 + 1680 = 480 + 3360.

The Tetrad (4) determines both 1920 and 3840 because

3840 = 16×240 = 4²(1+2+3+4)×1×2×3×4,

1920 = 64×30 = 8²(1²+2²+3²+4²) = 8² + 16² + 24² + 32².

8. (1920+1920=3840) lines & triangles make up the Type B Petrie polygons
in the Coxeter projections of the two 4₂₁ polytopes representing E₈×E₈

A Type B 30-gon has 30 sectors that are Type A triangles. The Type A 30-gon has 30 red corners & 60 red sides of sectors. One green corner & 3 green sides of 3 green triangles, i.e., 7 geometrical elements, are added to each sector of the Type B 30-gon, which has 10 geometrical elements (5 sides and 5 corners & triangles). This 3:7 division corresponds to the distinction in the Tree of Life between the Supernal Triad and the 7 Sephiroth of Construction and in the tetractys to the 3 yods at its corners and its 7 hexagonal yods. The corner inside each sector corresponds to Malkuth (central hexagonal yod of the tetractys) and the 2 sets of 3 lines/triangles correspond, respectively, to the two triads: Chesed-Geburah-Tiphareth & Netzach-Hod-Yesod (the two triangular sets of 3 corners formed by the 6 hexagonal yods on the sides of the tetractys). (240×10=2400) corners, sides & triangles surround the centres of the 8 triacontagons; they comprise (240×3=720=72×10) red corners & sides and (240×7=1680=168×10) green corners, sides & triangles. In terms of the root composition of E₈, the division: 240 = 72 + 168 signifies the 72 roots of E₆ and the remaining 168 roots that belong to the 240 roots of E₈. 240 (=24×10) red corners and 24×10 red lines form the sides of the 8 triacontagons; 24×10 red lines and 168×10 green corners, sides & triangles are inside them. Therefore, (240+240=480=48×10) corners & lines are external and (240+1680=1920) corners, sides & triangles are internal, where

240×10 = 48×10 + 192×10 = 48×10 + 24×10 + 168×10 = (48+24+168)×10.

The division:

240 = 24 + 48 + 168

signifies the 48 roots of F₄, a subgroup of E₆, the remaining 24 roots of E₆ and the 168 roots that are not roots of E₆, i.e., there are 192 roots that are not roots of F₄.

The division

1920 = 240 + 1680

appears in the 30 triacontagons making up the E₈ Coxeter projection of the second 4₂₁ polytope representing the symmetries of the second E₈ group predicted by E₈×E₈ heterotic superstring theory. We see that this direct product of two E₈ groups is the manifestation in a superstring context of the divisions:

3840 = 1920 + 1920

and

384 = 192 + 192

existing for holistic systems and embodied in sacred geometries.

The (7+7) polygons of the inner form of the Tree of Life constitute a holistic system because (192+192=384) geometrical elements surround their centres. The division: 192 = 24 + 168 is due to the 24 geometrical elements in the hexagon and to the 168 remaining elements. (1920+1920=3840) geometrical elements surround the centres of the (70+70=140) polygons enfolded in 10 Trees of Life. The (10+10=20) hexagons have (240+240=480) geometrical elements and the (60+60=120) other polygons have (1680+1680=3360) geometrical elements.

The divisions:

3840 = 1920 + 1920

and

1920 = 240 + 1680,

i.e., the divisions:

3840 = 240 + 1680 + 240 + 1680 = 480 + 3360,

characterise holistic systems such as sacred geometries. They manifests naturally in the 4₂₁ polytope and in a pair of such polytopes, which is therefore a holistic object. As the 4₂₁ polytope represents the 240 roots of E₈, this implies that E₈×E₈ conforms to this pattern exhibited by sacred geometries. They also imply the division:

2400 = 480 + 1920 = 480 + 240 +1680 = 720 + 1680.

The 240 roots of E₈ comprise the72 roots of its exceptional subgroup E₆ and168 other roots. The72 roots contain the48 roots of F₄ and 24 other roots. So, apart from the factor of 10, the division characteristic of sacred geometries mirrors the group-theoretical fact that the 240 roots of E₈ contain the48 roots of F₄ and (24+168=192) other roots, whilst the 480 roots of E₈×E₈ contain (192+192=384) roots other than the (48+48=96) roots of the two F₄ groups. The factor of 10 arises from the 10 dimensions of superstring space-time, so that every one of the 240 Yang-Mills gauge fields coupling to the gauge charges associated with the 240 roots of E₈ has 10 space-time components. It means that there are 1680 space-time components of the168 Yang-Mills gauge fields associated with the168 roots of E₈ that are not roots of E₆. A connection is therefore established between the superstring structural parameter 1680 reported by C.W. Leadbeater in his bookOccult Chemistryfor the UPA (identified by the author as the subquark state of the E₈×E₈ heterotic superstring) and the root composition of E₈, which conforms to the holistic pattern exhibited by sacred geometries.

The (60+60=120) Type A polygons of the first 6 types enfolded in 10 Trees of Life have (1920+1920=3840) yods. They comprise (240+240=480) corners and (1680+1680=3360) other yods.

Outside the root edge of the (7+7) enfolded, Type D polygons are (1920+1920=3840) sides of (1269+1269=2538) triangles. The 2 Type D hexagons have (240+240=480) sides besides the (6+6=12) sides of the sectors of the 2 enfolded triangles when they are Type A. The other (6+6) enfolded, Type D polygons have (1680+1680=3360) sides.

When the 50 faces of the 5 Platonic solids are Type A regular polygons, 1920 yods line their axes and sides of sectors. Of these, 240 yods are corners that are not vertices surrounding their axes. This leaves 1680 yods (840 yods in each set of 5 halves of the solids). On average, 384 yods line the axis and sides of tetractyses in the faces of a Platonic solid (192 yods in each half).

Twenty-nine polyhedra can be fitted to the 62 vertices of the disdyakis triacontahedron. When their faces are Type A polygons, they have 3840 hexagonal yods. Each set of halves of the 29 polyhedra has 1920 hexagonal yods (240 in the icosidodecahedron and 1680 in the other 28 polyhedra).

When they are Type B triangles, the 43 triangles in the 3-d Sri Yantra contain 1920 yods other than the 16 corners & centres of the 9 triangles in the central triangle. They comprise 240 yods that are either hexagonal yods of the central triangle, points of the 42 triangles or their internal corners, as well as 1680 yods that are either hexagonal yods in the 42 triangles or corners shared by adjacent triangles in each layer of triangles.

The 240 vertices of the 8-d 4₂₁ polytope mark the positions in E₈ lattice space of the 240 non-zero roots of E₈, the rank-8 exceptional Lie group. They have (8×240=1920) coordinates. The (240+240=480) vertices of 2 similar, 4₂₁ polytopes map the (240+240=480) roots of E₈×E₈. They have (1920+1920=3840) coordinates. Their counterpart in the inner form of 10 Trees of Life are the (1920+1920=3840) corners, sides & triangles surrounding the centres of the (70+70) separate polygons.

The Petrie polygon for the E₈ Coxeter plane projection of the 4₂₁ polytope is the triacontagon with 30 corners. When Type B, the 8 concentric triacontagons making up this projection have (8×30×10=2400) corners, sides & triangles surrounding their centre. (8×30×2=480) points & lines form their sides, inside which are (8×30×8=1920) points, lines & triangles. They comprise 240 lines that are part of the 8 Type A triacontagons and (240×7=1680) additional points, lines & triangles.