#18 The musical character of the E₈- & E₈′-singlet states of the E₈×E₈′ heterotic superstring

We pointed out in #2 that the sum of the 20 number weights making up the Tetrahedral Lambda = 50×(7N/6), where N is the integer at the centre of the Lambda Tetractys that is its first face and N/6 is the tone ratio of the note at its apex. (To create the general form when N, rather than 6, is at the centre of its first face, we simply multiply every weight by N and then divide by 6). The sum of the weights at the centres of its four faces = 50N/6 (let us call this "S"), so that the total sum is seven times this (7S). The sum of the weights at its four vertices = 100N/6, which is 2S, whilst the sum of the remaining 12 weights on its edges is 200N/6, which is 4S, where 7S = S + 2S + 4S. The sum of the 16 weights on the six edges is 300N/6, which is 6S. This property can be represented by the seven corners of the six sectors of a hexagon with the number S assigned to each corner. Its centre corresponds to the centres of the four faces and its six corners correspond to the 16 others weights, which sum to 6S. Alternatively, as the hexagon is the Petrie polygon of the octahedron, the 1:2:4 pattern results by assigning S to the centre of this polyhedron, to two diametically opposite vertices and to the four vertices that are the corners of a square. S is 50 times the value of the tone ratio N/6 at the apex of the Lambda Tetractys, where 50 is the number value of ELOHIM, the Godname of Binah. The sum of the 10 number weights in the first face is 90N/6 = 15N, where 15 is the number value of YAH, the shorter version of the Godname assigned to Chokmah. The sum of the 10 number weights in the second, third & fourth faces = 350N/6 − 90N/6 = 260N/6 = 26×10N/6, where 26 is the number value of the full Godname assigned to Chokmah. The sum of the number weights at their centres = 50N/6 − N = 44N/6. Therefore, the sum of the seven number weights that line edges and are outside the first face = 260N/6 − 44N/6 = 216N/6 = 36N, where 36 is the number value of ELOHA, the Godname of Geburah. The sum of the 16 number weights lining all edges = 300N/6 = 50N. The number value 50 of ELOHIM determines the sum of the 16 number weights that shape the Tetrahedral Lambda by their lining its six edges, whilst the number value 36 of the Godname of the Sephirah directly below Binah in the Tree of Life determines the sum of the seven number weights outside its first face; these shape the other faces. The sum of the seven number weights at all vertices and all centres of faces except the fourth face containing the weight 24N/6 = 100N/6 + 50N/6 − 24N/6 = 126N/6 = 21N, where 21 is the number value of EHYEH, the Godname of Kether. These and all the other Godnames prescribe the Tetrahedral Lambda because it is an archetypal object that belongs to Atziluth (the Archetypal World), being an arithmetic form of the divine blueprint that takes the geometrical forms of the Tree of Life and the Sri Yantra. Its detailed prescription by the Godnames assigned to the 10 Sephiroth is analysed here.

When N = 288, we found in #2 that the Tetrahedral Lambda is an arithmetic represention of the number (16800) of turns of the 10 whorls of the UPA (the subquark state of the E₈×E₈′ heterotic superstring) because 50×288/6 = 2400, so that the total sum of the 20 tone ratios = 7×2400 = 16800. The centres of the seven Type A polygons in each half of the inner Tree of Life are surrounded by 288 yods. This yod population therefore is the magnitude of a tone ratio of a note in the Pythagorean musical scale that makes the Tetrahedral Lambda embody the number of circularly polarised oscillations making up the basic constituent of atomic nuclei. The reader should realise that this joining together of sacred geometry, the Pythagorean musical scale and superstring physics is remarkable. The note at the apex of this unique Tetrahedral Lambda is (288/6=48), which is the number of corners of the seven polygons, as well as the number value of Kokab, the Mundane Chakra of Hod. Notice that the musical weights at, respectively, the centre and apex of the Lambda Tetractys are N and N/6, i.e, the former is six times the latter. This should be compared with the formula Y(n) = 6n for the number of yods (Y) surrounding the centre of the Type A n-gon with n corners. The central musical weight of a Lambda Tetractys with N at its apex always measures the number of yods surrounding the centre of a single N-gon (or the centres of several such polygons with N corners). In order for the apex N/6 of a Lambda Tetractys with N at its centre to be an overtone, N must be an integer multiple of 6. Counting the overtones in the table of tone ratios of the notes of the Pythagorean scale, we find that 24 is the fourth such overtone and 288 is the 15th. Hence, the Godname YAH with number value 15 picks out the very overtone in the table for which the sum of the 20 tone ratios in the Tetrahedral Lambda with N = 288 is 16800 — the number of oscillations determined in the UPA that was remote-viewed by Besant & Leadbeater! This is remarkable evidence supporting our analysis. No note — whether overtone or partial — can generate the number 10080 in the same way because this number is 3/5 of 16800 and there is no Pythagorean note that is an integer multiple of 5. There is also no note for which the sum (350N/6) of all the tone ratios in the Tetrahedral Lambda is 2016 — the number of circularly polarised oscillations in each whorl of the shadow matter superstring described by Ron Cowen. However, we did find earlier that the number (10080) of turns in this subatomic particle is embodied in the Tetrahedral Lambda when N = 288 as the sum of the 10 number weights lining three of the six edges of the tetrahedron. The average of all 20 tone ratios = 16800/20 = 840, whilst the average of the 10 tone ratios = 10080/10 = 1008. We see that the averages of the tone ratios are, in each case, the numbers of turns in half a whorl of each superstring. This reflects the facts that:

1. the number (20) of half-whorls in the UPA is the number of tone ratios in the Lambda Tetrahedron;
2. the number (10) of half-whorls in the shadow matter particle is the number of tone ratios lining three of its edges.

Any reader who is suspicious that it could be just due to chance that a subset of the 20 number weights exists whose weights add up to 10080 should have his doubts dispelled when he asks himself how likely it is that the number of number weights in that subset should also by chance be precisely that which generates the number of turns in half a whorl as the arithmetic average of these number weights.

The superstring & Kabbalistic meaning of the number 32
The 10 Sephiroth and the 22 Paths of the outer Tree of Life are the "Thirty-two mystical paths of wisdom" described in the opening lines of the Sepher Yetzirah. All three numbers appear in string theory as the 10 dimensions of superstring space-time, the 22 compactified dimensions required by bosonic strings and the 32 components of the Dirac wave function of a fermion in 10-d space-time. In general, the number of components of its wave function in d-dimensional space-time = 2^d/2; d = 10 for a fermionic superstring, so that its wave function has (2⁵=32) components. This number also appears in the inner Tree of Life because the sum:

1 + 2 + 3 + ... + 32 = (1+32) + (2+31) + (3+30) +... + (16+17) = 33 + 33 + 33 +... + 33 = 8×33 + 8×33 = 264 + 264 = 528

is the number of yods in both sets of seven enfolded Type A polygons when each set with 264 yods is considered separate, not joined to each other at the root edge. This arithmetic connection between the number 32 and the number 528 as the 32nd triangular number illustrates the sacred nature of 528. Its meaning vis-à-vis CTOL is that it is the number of SLs down to the top of the 3-tree mapping the three "dense physical" subplanes, that is, the material universe revealed by the five human senses. As 528 = 16×33, where 33 = 1! + 2! + 3! + 4!, it is expressed by the four integers 1, 2, 3 & 4 symbolised by the four rows of dots in the tetractys as

4²(1! + 2! + 3! + 4!) = 4² + 4²(2! + 3! + 4!).

4² (=16) is the number of yods in both sets of polygons of the inner Tree of Life that are shared with the Paths of the outer Tree of Life, so that

4²(2! + 3! + 4!) = 528 − 16 = 512

is the number of unshared yods in the two sets (256 (=4⁴) yods in each one).

36 yods line the 12 sides of the Type A dodecagon. Of these, 32 yods shape it because they extend outside the side shared with the 13 other polygons. It is one of the many ways that illustrate how the dodecagon is the polygonal counterpart of the outer Tree of Life, for its 32 boundary yods outside the root edge correspond to the 32 "mystical paths of wisdom," being made up of 10 corners and 22 hexagonal yods that are analogous to the 10 Sephiroth and 22 Paths.

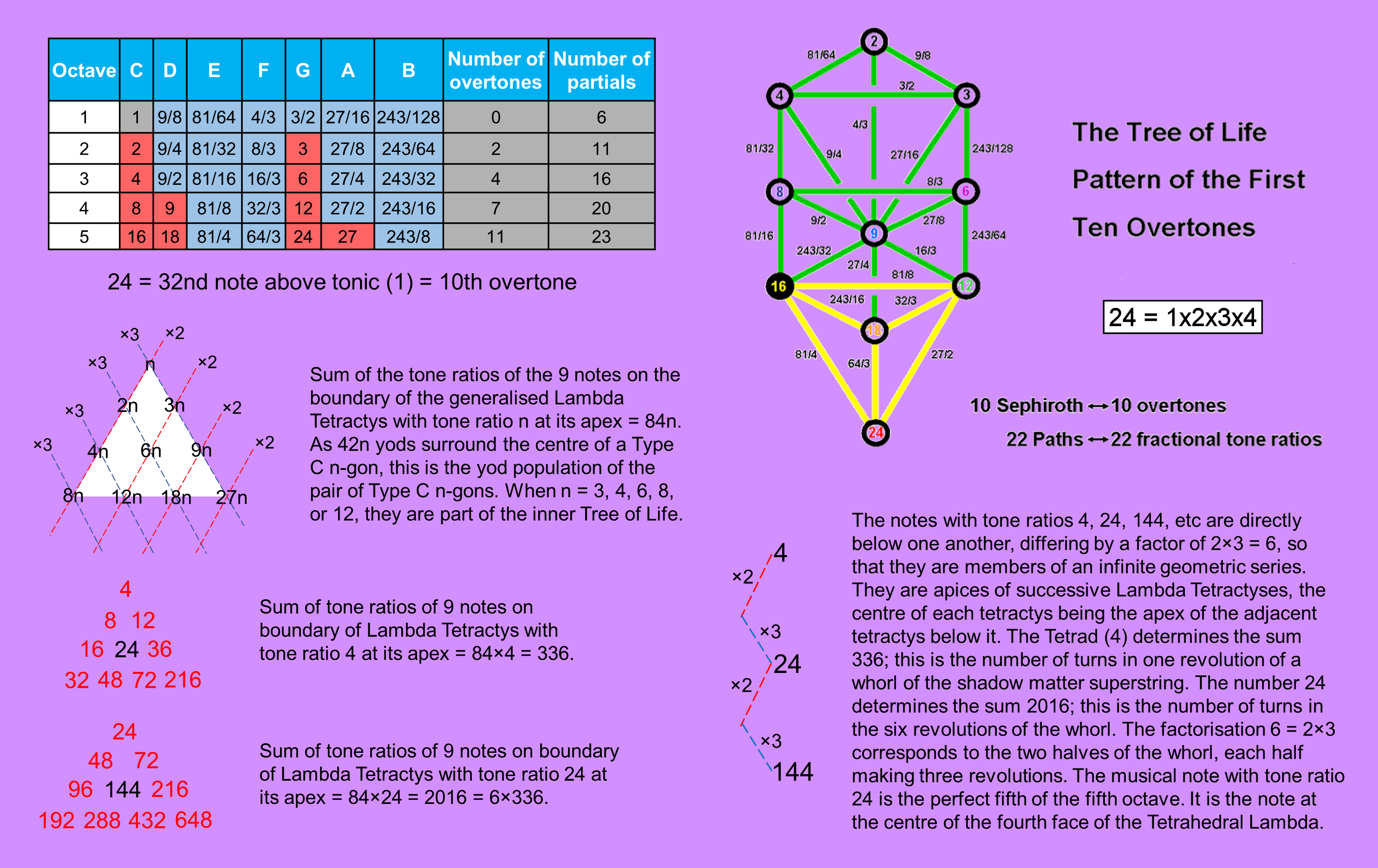
If we inspect the table of tone ratios of the notes of the Pythagorean musical scale (see picture above), we find that there are 10 overtones (red cells) up to (and including) the 32nd note above the tonic of the first octave. It has the tone ratio 24 and is the perfect fifth of the fifth octave. Below this note are (32−10=22) inharmonic partials with fractional tone ratios (blue cells). This 10:22 pattern is analogous to the 10 Sephiroth and 22 Paths of the outer Tree of Life. Indeed, it is more than merely analogous — it demonstrates that the 32nd note above the tonic represents the completion of the musical counterpart of the universal Tree of Life blueprint; it is its "Malkuth", so to speak. This is why the number weight 24 is at the centre of the tetractys forming the fourth face of the Tetrahedral Lambda with 1 at its apex. One can liken the four tetractyses to the four "Worlds" described in the Kabbalah that are the four stages in the physicalisation of the divine archetypes. The first face corresponds to the archetypal World of Aziluth and the last corresponds to the material universe of Assiyah. Its Malkuth, musically speaking, is the 10th overtone with tone ratio 24. In view of this, it should come as no surprise that the 1680 oscillations in each whorl of the UPA, which is the Malkuth aspect of the Tree of Life at the subatomic level, are the string manifestation of 24 gauge charges of the unified symmetry group E₈, as has been explained in many areas of this website.

The numbers in the general Lambda Tetractys are tone ratios, measuring the relative number of oscillations compared with that of the first harmonic. The sum of the tone ratios of its 10 notes = 90n, where n is the tone ratio of the note located at its apex. The central note has the tone ratio 6n, so that the sum of the tone ratios of the nine notes on the boundary of the tetractys is 84n. The centre of the Type C n-gon is surrounded by 42n yods. Two such n-gons have 84n yods. Five of the seven types of polygons in the inner Tree of Life have numbers of corners that are tone ratios of notes in the Pythagorean scale. They are the triangle (n=3), square (n=4), hexagon (n=6), octagon (n=8) & dodecagon (n=12). The pentagon (n=5) and decagon (n=10) have no Lambda Tetractys counterparts because 5 and 10 are not Pythagorean overtones. As the number 5 is a prime number, neither 5 nor 10 can be factorised as 2^p3^q, where p = 0, ±1, ±2, etc and q = 0, ±1, ±2, etc.

The sum of the nine tone ratios on the boundary of the Lambda Tetractys with N at its centre is 14N. The Tetrad determines the number (336) of oscillations per revolution of a whorl because, when the number 4 is the apex of the Lambda Tetractys, N = 4×6 = 24 and the sum of the boundary tone ratios = 14×24 = 336. It also determines the number of oscillations in a whorl of the shadow matter particle because, when 24 (=4!) is the apex of the Lambda Tetractys, N = 24×6 = 144 and the sum of the boundary tone ratios = 14×144 = 2016. In fact, the apex of this tetractys is the centre of the previous one. The tone ratios in each Lambda Tetractys that grows vertically down out of the one above it in the infinite, 2-d, hexagonal lattice of tone ratios are six times their counterparts in the parent one, the factor of six arising from the product of the factors 2 and 3 that generate all the tone ratios. Therefore, 144 = 2×3×24 and 2016 = 14×144 = 2×3×14×24 = 2×3×336. This factorisation manifests in the whorl of the shadow matter particle as the three revolutions it makes in an outer spiral and the three revolutions in the inner spiral, i.e., a pair of three revolutions, each revolution comprising 336 circularly polarised waves along which are spread eight E₈′ gauge charges, 42 oscillations per charge. The oscillatory form of the shadow matter particle conforms to the mathematics of the generation of notes in the Pythagorean musical scale. Why? Not, of course, because whorls are sound waves but because both matter and the notes of music conform to a universal mathematical pattern whose arithmetic expression is the Tetrahedral Lambda. The inner Tree of Life is one of its geometric expressions, for the (7+7) enfolded, Type A polygons have 350 hexagonal yods lining their 94 tetractyses, just as the sum of the 20 number weights in the Tetrahedral Lambda is 350 when its apex is the number 1. The detailed correspondences between them are discussed here. The sum of the 20 number weights in the Tetrahedral Lambda = 350N/6, where N is the weight at the centre of its first face and N/6 is the weight at the apex of this triangle. The number of hexagonal yods in the 14n Type A polygons belonging to the inner form of n overlapping Trees of Life = 350n. The number weight at the apex can be interpreted as signifying the number of Trees of Life whose inner form has a hexagonal yod population that equals the sum of the 20 number weights. This equivalence holds only for integers n that take the musical form n = 2^p3^q, i.e., the overtones of the Pythagorean musical scale, including the first harmonic n =1. When n = 48 (the 14th overtone and the 15th harmonic), the number of hexagonal yods in the (14×48=672) polygons making up 48 Trees of Life = 350×48 = 16800, which is the number of circularly polarised oscillations in the 10 whorls of the UPA. This demonstrates how the Godname YAH of Chokmah with number value 15 prescribes the structural parameter 16800 of the E₈×E₈′ heterotic superstrings that compose up and down quarks — what Besant & Leadbeater called, respectively, the "positive hydrogen triplets" and the "negative hydrogen triplets" (see here). The number of circularly polarised oscillations in the standing waves of the helical whorls of the UPA is, simply, the sum of the 20 number weights of a Tetrahedral Lambda with the number weight 48 at its apex and the number weight 288 at the centre of its first face. The inner Tree of Life counterpart of this is the 288 yods that surround the centres of the seven Type A polygons with 48 corners. The factor of 6 between the numbers 48 and 288 arises in the first face because its central number weight is always six times the number weight at its apex; it arises in the seven Type A polygons because the number of yods surrounding the centre of each polygon is six times the number of its corners. The Tetrahedral Lambda with 1 at its apex is the counterpart of the inner form of each overlapping Tree with 350 hexagonal yods lining its tetractyses; with n at its apex, it is the counterpart of the 350n hexagonal yods lining tetractyses in the inner form of n Trees of Life. As the number of yods in the n-tree ≡ Y(n) = 50n + 30, the number of yods in the outer form of every 7n Trees = 50×7n = 350n. The same expression applies to the outer form of every 7n Trees, just as it does to the inner form of every n Trees. One can interpret this as the inner Tree of Life encoding the sevenfold emanation of the outer Tree of Life. Why sevenfold? Because the seven subplanes of each of the seven planes of consciousness are mapped by seven Trees, so that the inner form of each Tree in COL encodes for a whole plane mapped by seven Trees. In particular, the inner form of the 7-tree mapping the physical plane contains (7×350=49×50) hexagonal yods lining tetractyses, and this is the number of yods in every 49 Trees, i.e., between the 1-tree and the 50-tree, which is the source of the 49-tree mapping the cosmic physical plane. This illustrates the Hermetic axiom "As above, so below."

As 351 is the 26th triangular number number:

1 + 2 + 3 + ... + 26 = 351,

where 351 is the number value of Ashim ("Souls of Fire"), the Order of Angels assigned to Makuth, the number 350 is the sum of the first 25 integers after 1 that can be assigned to the 25 yods in a Type A square:

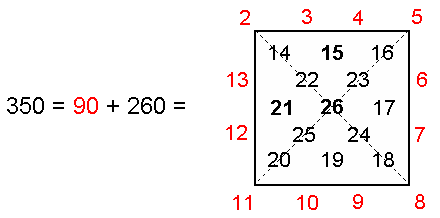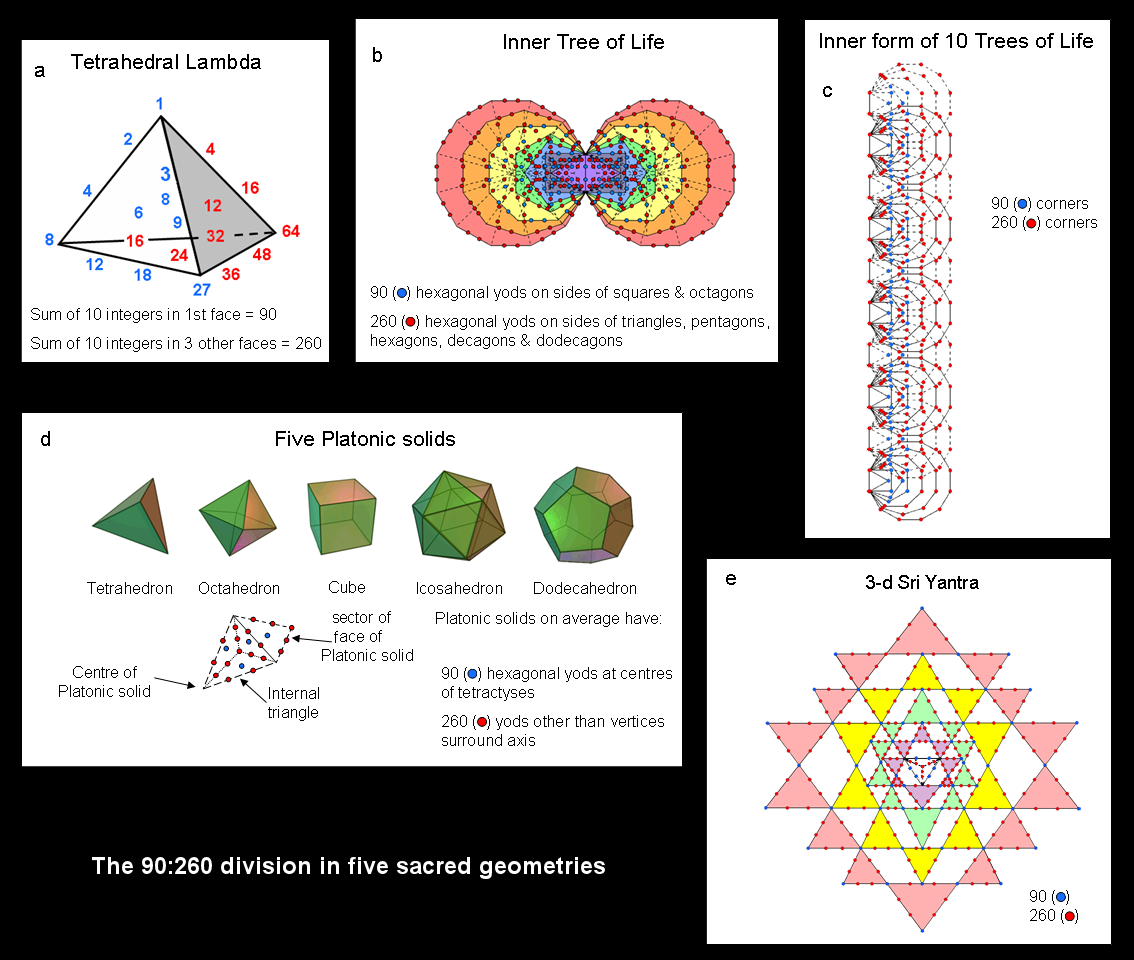The square symbolises the Tetrad (4), and therefore this illustrates the Tetrad Principle discussed in Article 1 governing parameters of holistic systems that embody sacred geometry. Notice, firstly, that the sum of the 12 red integers on its perimeter is 90, which is the sum of the 10 number weights in the first face of the Tetrahedral Lambda with 1 at its apex, and, secondly, that the sum of the 13 remaining black integers is 260, which is the sum of the 10 number weights in its second, third & fourth faces (see (a) in the diagram shown above). This 90:260 division is characteristic of the number 350 when it is embodied in sacred geometries. For example:

• the 350 hexagonal yods lining tetractyses in the (7+7) enfolded Type A polygons of the inner Tree of Life comprise 90 blue hexagonal yods of this type in the squares & octagons and 260 red hexagonal yods in the triangles, pentagons, hexagons, decagons & dodecagons (see (b));
• the 70 polygons with 350 intrinsic corners that make up the inner form of 10 Trees of Life consist of triangles, squares, pentagons & hexagons with 90 blue corners outside their root edges and octagons, decagons & dodecagons with 260 red corners (see (c));
• when the faces and interior triangles of the five Platonic solids are Type A polygons, there are on average 90 blue hexagonal yods at the centres of tetractyses and 260 red yods other than vertices surrounding the axis of the Platonic solid (see (d));
• when they are tetractyses, the 42 triangles surrounding the central triangle of the 3-d Sri Yantra have 84 blue corners and 252 red hexagonal yods lining them. Above the centre of the central triangle is the bindu. Six blue hexagonal yods line its sides. Six red hexagonal yods line the sides of its sectors. (84+6=90) blue hexagonal yods and (252+2+6=260) yods make up the 350 yods (see (e)).

As well as being the number of yods surrounding the centres of the seven separate Type A polygons making up each half of the inner Tree of Life, the number 288 is the number of yods surrounding the centre of a square whose sectors are 2nd-order tetractyses:

288 =

The square therefore embodies the very number that, when it is the number weight of the 28th overtone at the centre of the first face of a Tetrahedral Lambda, generates the number (16800) of circular turns in the 10 helical whorls of the UPA as the sum of the 20 number weights in this tetrahedron. The square contains 248 hexagonal yods, where 248 is the number value of Raziel, the Archangel assigned to Chokmah, the second Sephirah of the Tree of Life:

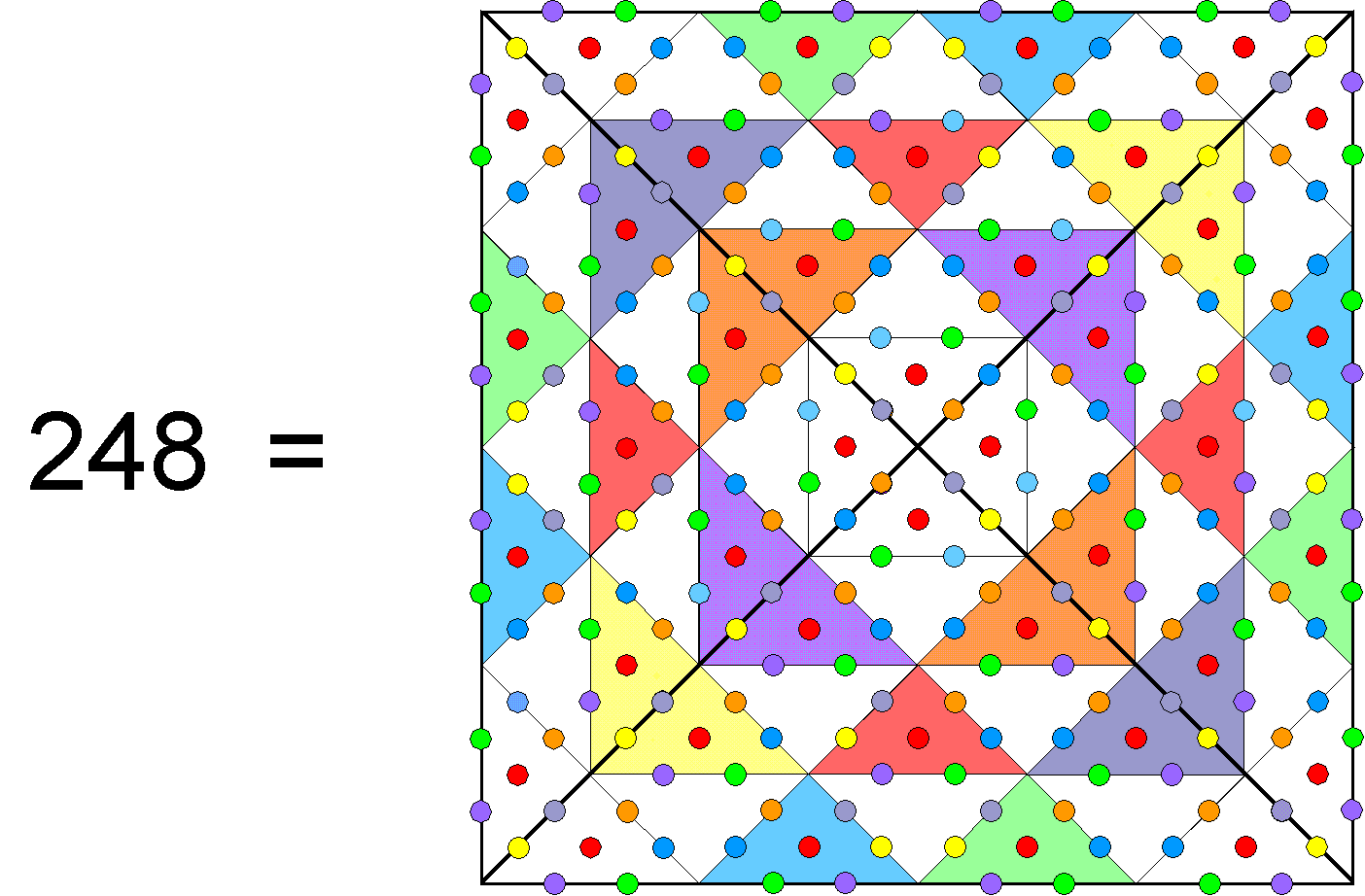
We see that the square embodies the dimension 248 of the exceptional Lie group E₈ that is the unified symmetry group of the E₈×E₈′ heterotic superstring, of which the UPA is the ground state of the subquarks in its E₈′-singlet sector. The Type A square embodies the number (25) of spatial dimensions of bosonic strings because it has 25 yods, the number of gauge fields of E₈ and the number 288 that generates via the Tetrahedral Lambda the number (16800) of circularly polarised oscillations in the 10 whorls of the subquark state of the E₈×E₈’ heterotic superstring. The conjunction of three numbers (one of paranormal provenance and two established in pure mathematics and string theory) cannot be, plausibly, attributed to chance. Instead, it illustrates the power of the Tetrad to define in both an arithmetic and a geometric manner parameters of holistic systems like the superstring (see the discussion of the Tetrad Principle in Article 1). It is symbolised by the square and the tetractys, which was the focus of the oath of allegiance of the ancient Pythagoreans to their teacher:

"I swear by the discoverer of the Tetractys,
Which is the spring of all our wisdom,
The perennial fount and root of Nature."

The ancient doctrine of the four Elements Earth, Water, Air & Fire is merely the exoteric expression, when properly understood, of this core principle of a fourfold, mathematical pattern governing all things from the microscopic level to the macroscopic domain — one whose natural geometrical symbol is the square. The four dimensions of Minkowski's space-time continuum that Albert Einstein exploited in his Theory of Special Relativity, the four Jungian cognitive functions of intuiting, thinking, feeling and sensing and the four nitrogen bases labelled A, G, C & T that form the protein-encoding codons strung along the two helices of the DNA molecule are examples of this basic principle in action. The four Kabbalistic Worlds of Atziluth, Beriah, Yetzirah & Assiyah are the metaphysical expression of this principle. The tetractys has always been regarded by scholars as a symbol of the four-foldness that the ancient Pythagoreans believed pervaded nature. The problem has been that the former understand it as no more than a symbol, for they have never realised that it is far more than that, being the "Rosetta Stone" that deciphers the analogous information encoded in sacred geometries and reveals their mathematical isomorphism. To realise that, one has to accept in principle (and then be able to recognise) the existence of transcendental design as the only possible explanation of this isomorphism. But many scientists are reluctant to take even this first step — at least publicly — because it means straying in their work from the straight path of scientific materialism into the uncharted waters of religion, which most scientists mistakenly believe makes assertions whose truth is always a matter of faith, not of evidence provided by the five senses. They fail to realise that mathematics — the very tool that may be essential to their daily work — can prove assertions that they wrongly judge are unscientific because they seem to be unfalsifiable. Only the diehard empiricist needs his hands and eyes to prove that something is real. The existence of transcendental design is not a matter of faith, opinion or interpretation when it takes concrete, mathematical form. Unlike the evidence of the senses, which can be anbiguous or even to be doubted on rare occasions as hallucinatory, the mathematical evidence provided by isomorphic patterns found in sacred geometries cannot be denied. Put simply: it just is — and that existential reality demands explanation for why it is as it is. The sceptic cannot dismiss this plethora of beautiful design by suggesting that it either was fabricated, occurred by chance, was contrived by cherry-picking or amounts to nothing more than playing with numbers and geometrical shapes. Who can sensibly conclude that it is just a matter of coincidence that each half of the shadow matter particle (E₈-singlet state of the E₈×E₈′ heterotic superstring) is predicted by the author to have 7! circularly polarised oscillations that are the string manifestation of 120 (=5!) gauge charges of E₈′, there being 24 (=4!) charges per half-whorl? The eight triacontagons formed by the 240 vertices of the 4₂₁ polytope that represent the 240 roots of E₈′ have 10080 yods surrounding their centres when they are Type C because there are 42 yods per sector and 240×42 = 10080 (see #11). Who can regard as due to mere chance this mathematical reproduction of the 10080 oscillations predicted to make up the shadow matter particle, when it is in the context of the very gauge symmetry group E₈′ that is supposed to be associated with the paranormally described shadow matter particle if — as the author claims — it belongs to the E₈-singlet sector of the E₈×E₈′ heterotic superstring? Even a sceptic must admit (if he is sensible) that perpetually dismissing evidence of mathematical design as due to chance will fail to convince the neutral observer.

Summary

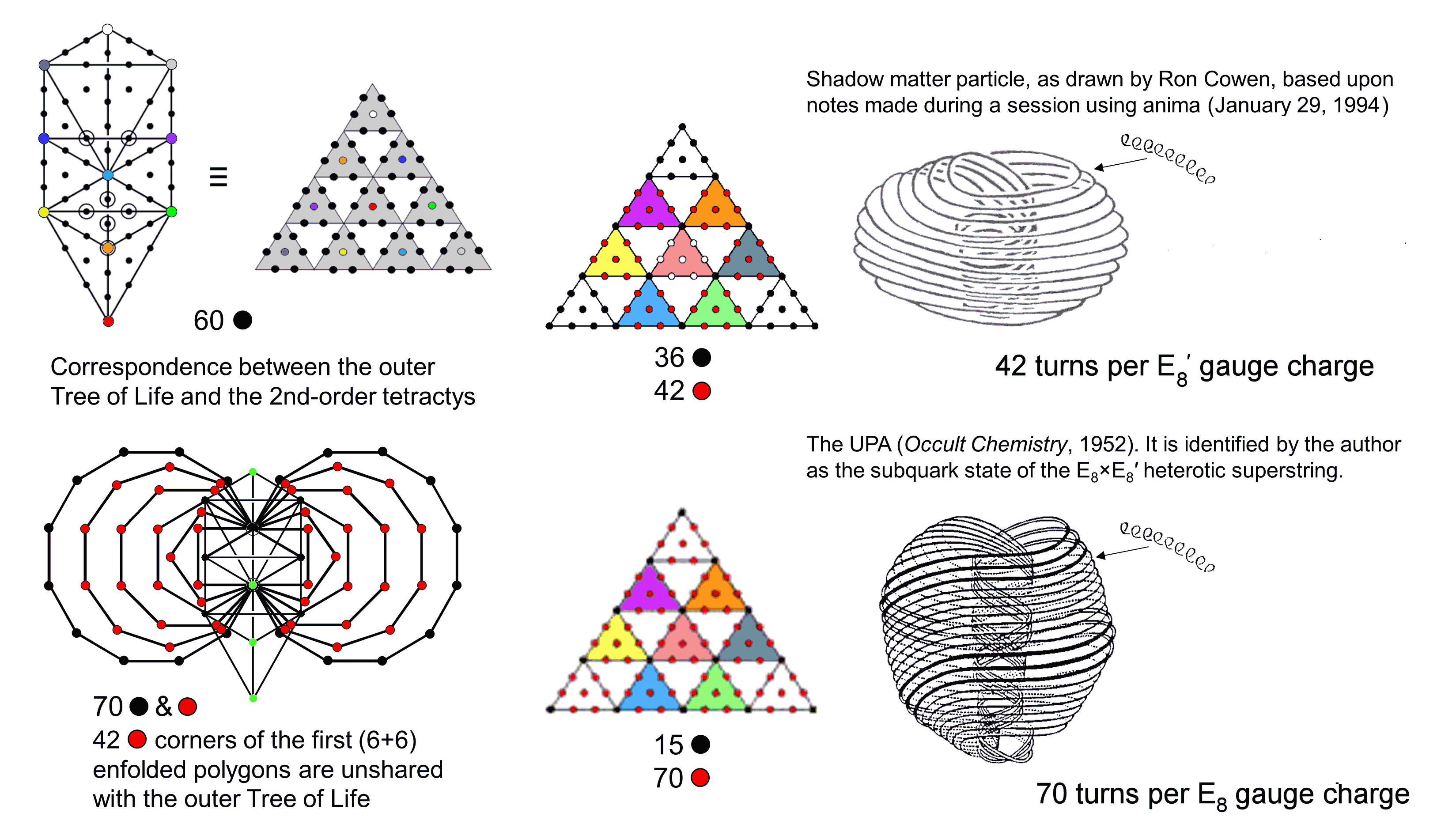
When its 16 triangles are tetractyses, the outer Tree of Life has 70 yods. Ten yods are located at the corners of tetractyses, leaving 60 hexagonal yods. This 10:60 (=1:6) division expresses the distinction between Malkuth, symbolised by the hexagonal yod at the centre of the tetractys, and the 6 higher Sephiroth of Construction, symbolised by the 6 hexagonal yods at the corners of a hexagon. The same division is present in the 70 hexagonal yods in the 2nd-order tetractys, which comprise 10 coloured hexagonal yods at the centres of its 10 1st-order tetractyses and 60 black hexagonal yods. The former correspond to the 10 yods at corners of tetractyses in the outer Tree of Life and the latter correspond to its 60 hexagonal yods, with Malkuth symbolised by the red hexagonal yod at the centre of the central tetractys. The inner Tree of Life counterpart of these two isomorphic representations of holistic systems consists of (7+7) regular polygons with 70 corners. Corners of triangles in the outer Tree of Life are coloured green unless they coincide with corners of polygons, in which case they are coloured black, as are the corners of the two dodecagons. The first (6+6) enfolded polygons have 50 corners, of which 42 corners (coloured red) are outside the root edge and unshared with the outer Tree. They correspond to the (6×7=42) red hexagonal yods in the 6 coloured 1st-order tetractyses surrounding the central one with white hexagonal yods. These 6 tetractyses symbolise the 6 higher Sephiroth of Construction. Their counterparts in CTOL are the 42 subplanes of the six superphysical planes of consciousness. They are mapped by the 42 triangles in the Sri Yantra that surround its central one symbolising Shiva, Vishnu & Brahma. Their octonian counterparts are the 42 pairings (eiej) of the 7 unit imaginary octonions ei (i =1-7), whose algebra is that of SL(2,3), the group of 168 automorphisms of the Fano plane, which is the projective plane with the smallest order (2). The holistic parameters 42 & 70 manifest in the E8×E8′ heterotic superstring as the 70 circular turns per E8 gauge charge spread along the whorls of the UPA (subquark state of the E8′-singlet sector) and as the 42 turns per E8′ gauge charge carried by the whorls of the basic shadow matter particle (E8-singlet).

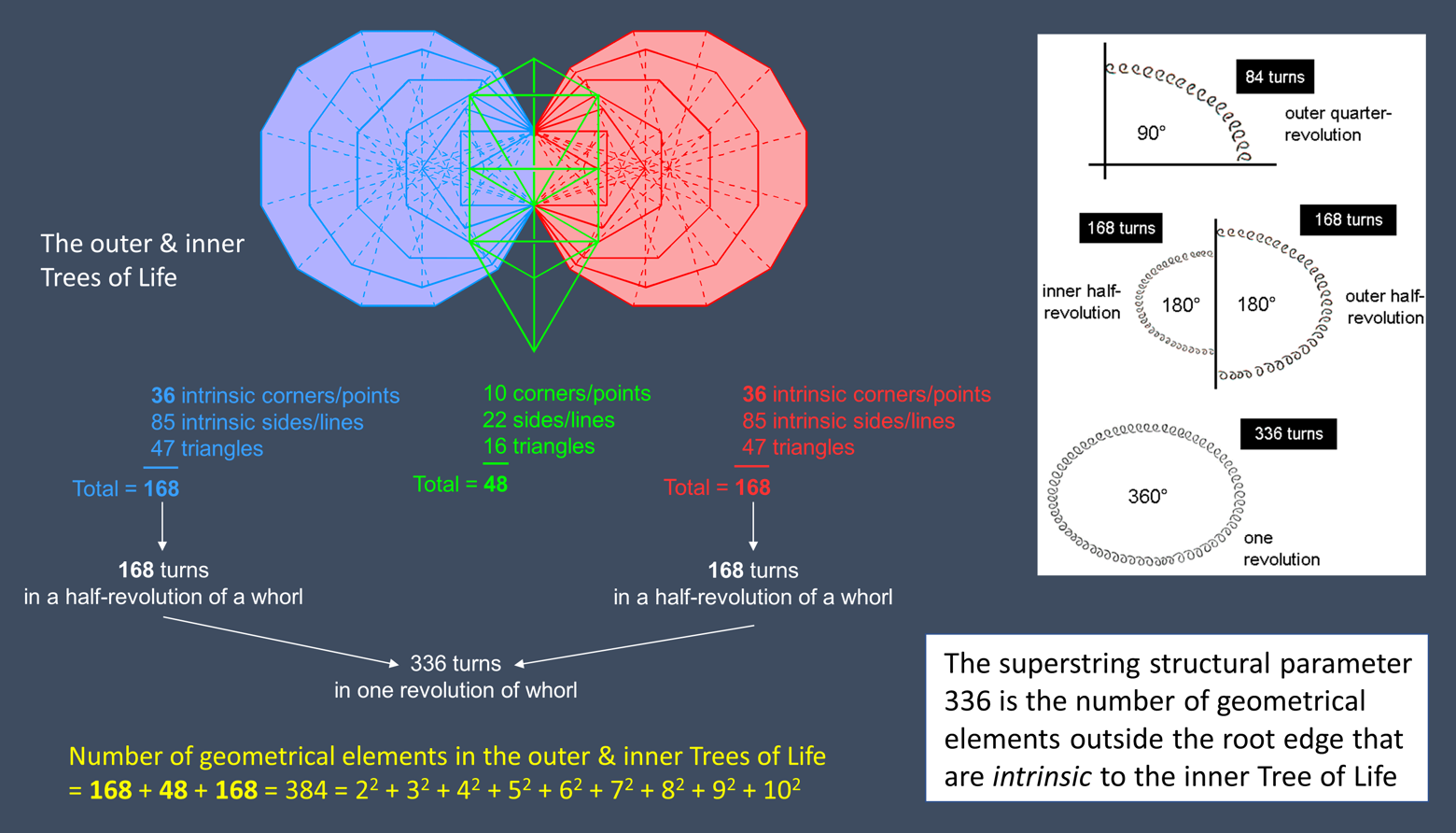
The 16 triangles of the outer Tree of Life have 10 corners and 22 sides — a total of 48 points, lines & triangles. The 47 triangles in each set of 7 enfolded Type A polygons making up the two halves of the inner Tree of Life have 41 corners and 88 sides. The top and bottom corners of each hexagon and their centres coincide with corners of triangles belonging to the outer Tree. The two vertical sides of sectors inside each hexagon coincide with sides of triangles that form the two side pillars of the outer Tree. Outside the root edge, each set of 7 enfolded polygons has 47 triangles with (41−1−2=36) unshared corners and (88−1−2=85) unshared sides, i.e., 168 unshared, geometrical elements. Intrinsic to the inner Tree of Life are (168+168=336) geometrical elements. This is how it embodies the superstring structural parameter 336 as the number of turns in one revolution of a helical whorl of both the UPA and the basic unit of shadow matter. The total number of geometrical elements making up the combined Trees of Life = 168 + 48 + 168 = 384 = 22 + 32 + 42 + 52 + 62 + 72 + 82 + 92 + 102. This number is also a defining parameter of holistic systems, e.g., the 384 lines & broken lines of the 64 hexagrams and the 384 points, lines & triangles that surround the centres of the (7+7) separate Type A polygons. It is the order of B4, the hyperoctahedral group of rotations & reflections in 4-d space, e.g., the number of distinct rotations and rotation-reflections that leave the 4-cube, the 16-cell & the 24-cell looking the same. The number 48 is the order of its subgroup B3, the octahedral group of symmetries in 3-d space that leave the octahedron and the cube looking the same. It is the number of lines & broken lines in the eight diagonal hexagrams of the 8×8 array of hexagrams, as well as the number of points, lines & triangles surrounding the centres of the two Type A hexagons that belong to the inner Tree of Life, the number of such geometrical elements in each subset of 6 polygons being 168. The inner Tree represents the extra rotations and rotation-reflections generated by the fourth spatial dimension, whilst the outer Tree, whose two halves have 24 geometrical elements, represents the 24 proper rotations & 24 rotations-reflections in 3-d space. As a circular turn ("1st-order spirilla") of each helical minor whorl of the UPA was ascertained by C.W. Leadbeater to be composed of 7 smaller turns ("2nd-order spirilla") wound on a torus, and so until the 7th-order spirilla, the number of turns per revolution of a minor whorl due to the 1st compactified dimension, the 2nd compactified dimension, etc is 336×71, 336×72, etc (each whorl winds around the 6 circular, compactified dimensions of 10-d space-time). As 336 = 7×48 = 7(72−1) = 73 − 71, the first number is 74 − 72 = 492 − 49. The number value 49 of EL CHAI ("Living God"), which is part of the Godname SHADDAI EL CHAI assigned to Yesod, the first Sephirah of Construction above Malkuth, determines the number of turns per revolution formed by the compactified dimension formally corresponding to Yesod, for the 7 orders of spirillae correspond to the 7 Sephiroth of Construction: 1st-order spirilla → 3-d space → Malkuth; 2nd-order spirilla → 1st compactified dimension → Yesod; 3rd-order spirilla → 2nd compactified dimension → Hod; 4th-order spirilla → 3rd compactified dimension → Netzach; 5th-order spirilla → 4th compactified dimension → Tiphareth; 6th-order spirilla → 5th compactified dimension → Geburah; 7th-order spirilla → 6th compactified dimension → Chesed. The 6 compactified dimensions generating the 6 higher orders of spirillae correspond to the 6 Sephiroth of Construction above Malkuth. They are symbolised in the 1st-order tetractys by the six dots forming the corners of a hexagon ("hexagonal yods") at the centre of which is the dot symbolising Malkuth, whose superstring counterpart is the 1680 1st-order spirillae that wind around the surface of a torus.

<< Previous    1...   16  17  [18]  19  20    Next >>

Home