| << Previous 1... 18 19 [20] 21 22 ...24 Next >> |
#20 How the 1-tree and the inner form of the 10-tree represent the 421 Polytope

The n-tree is the lowest n Trees of any set of overlapping Trees of Life. Constructed from tetractyses, it contains Y(n) yods, where
Y(n) = 50n + 30.
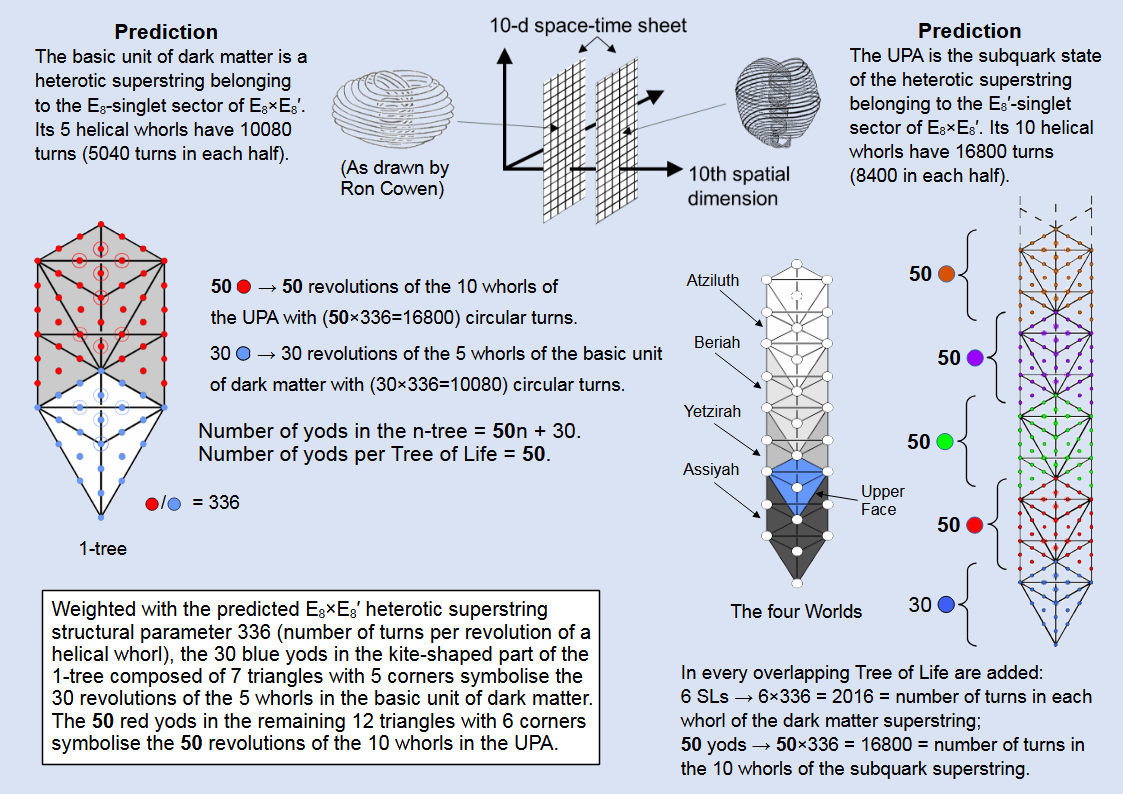
"30" is the number of blue yods in the white, kite-shaped quadrilateral shown in the picture above and "50n" is the number of remaining red yods. The number of yods in successive Trees of Life is 50 because Y(n+1) − Y(n) = 50. Hence, the Godname ELOHIM with gematria number value 50 prescribes how the form of the n-tree grows through the addition of successive Trees.
As the lowest of the 91 Trees of Life making up CTOL, the 1-tree containing 80 yods denotes its most Malkuth aspect, i.e., the physical realisation in the subatomic world of the cosmic blueprint. The two basic constituents of physical matter are the UPA, identified by the author as the E8'-singlet, subquark state of the E8×E8' heterotic superstring, and the particle discovered in the 1990s by the Canadian Buddhist Ron Cowen whilst investigating with micro-psi vision the subtle counterpart of his body (what Theosophists call the "etheric body", yogis call the "pranamayakosher" and Kabbalists call the "zelim"). This particle is identified by the author as belonging to the E8-single sector of E8×E8'. M-theory, which unites superstring theory with supergravity theories, predicts that space-time is 11-dimensional, with E8×E8' heterotic superstrings confined to either one of two parallel 10-d space-time sheets separated by a narrow gap spaced along the tenth spatial dimension, i.e., E8-singlet states are confined to one sheet and E8'-singlet states are confined to the other sheet, with only gravity able to act across the gap separating them. This implies that the matter of one sheet is optically invisible and impervious to the forces operating in the other sheet, apart from gravity. There exist two physical universes that share the same nine dimensions of space as distinct particles, one universe permeating the other but still separate from each other dimensionally so that no particle in one universe can occupy exactly the same point in 11-d space-time as the other because it would have to travel a small distance in the tenth dimension, which it cannot do. The author identifies the invisible matter belonging to this second universe as the mysterious "dark matter" that astronomers require to exist in order to explain the fast speeds of rotation of many galaxies. Cowen was describing the basic unit of dark matter. That is why the second physical but subtle body that humans have is invisible to their eyes.
According to Kabbalah, God's will acts in four primary stages called "Worlds". They are Atziluth (Archetypal World), Beriah (World of Creation), Yetzirah (World of Formation) and Assiyah (World of Action). The four Worlds (each spans many levels of being) correspond in a human being to the familiar division of the material body, the personality, soul and Spirit. Each World is represented by its own Tree of Life. The 1-tree represents the complete human physical form, comprising not only the body of flesh, bones and internal organs but also the invisible subtle body, or zelim, which is represented by the upper kite-shaped array of Sephiroth, known to Kabbalists as the "Upper Face".
Leadbeater & Besant described the UPA as having 10 whorls, each being a helix with 1680 turns that winds five times around the surface of a toroidal vortex. According to Cowen, his particle is composed of five whorls, each making six revolutions. He was unable to count how many turns each whorl has. However, the author has shown that sacred geometries divide naturally into two disjoint components whose yod or geometrical compositions are always in the ratio 6:5. The simplest example of this is shown by the formula for the number N(n) of SLs in the n-tree:
N(n) = 6n + 5
The 1-tree has N(1) = 11 SLs denoted by the five corners of the white kite-shape in the 1-tree shown above and the six remaining corners, which get repeated with every successive, overlapping Tree: N(n+1) − N(n) = 6. The number of yods in the n-tree ≡ Y(n) = 50n + 30. The number of yods in the 1-tree = Y(1) = 50 + 30 = 80 yods, where 80 is the gematria number value of Yesod, the penultimate Sephirah. The kite-shape contains 30 yods, leaving 50 yods in the rest of the 1-tree; as illustrated above, these get repeated in successive Trees. The 6/5 ratio appears in the geometry of the 1-tree because it has 19 triangles with 11 corners, i.e., it has 30 corners & triangles, and 25 sides, where 30/25 = 6/5. The ratio also appears in the Tree of Life because 10 straight lines are in its trunk and 12 straight lines are in its branches, where 12/10 = 6/5. As now explained, it appears as well in the polyhedral form of the Tree of Life (see Article 23 and here). This consist of what we call the "144 Polyhedron" (its polyhedral inner form) and the disdyakis triacontahedron, which is the Catalan solid with the largest number of vertices. The former has 74 vertices, 216 edges and 144 triangular faces; the latter has 62 vertices, 180 edges & 120 triangular faces. The two polyhedra manifest this ratio because 72 vertices surround the axis of the 144 Polyhedron and 60 vertices surround the axis of the disdyakis triacontahedron, where 72/60 = 6/5. Similarly, the 216 edges of the former and the 180 edges of the latter are in the ratio 6/5, as are their respective 144 faces and 120 faces. Because the 144 Polyhedron has 6/5 times as many vertices surrounding an axis, 6/5 times as many edges and 6/5 times as many faces as the disdyakis triacontahedron, it has 6/5 times as many geometrical elements surrounding its axis as the latter when they are Type A and their internal triangles formed by joining their centres to their vertices are Type B. The proof of this is as follows: using Euler's polyhedral formula for the V vertices, E edges & F faces of a polyhedron:
V − E + F = 2,
and, given that each vertex defines one internal side of a triangle and that each edge is the
side of an internal Type B triangle with three sectors, then:
1. number of corners of internal & external triangles surrounding an axis that passes through two vertices = V
− 2 + E = 2E − F,
2. number of sides of triangles surrounding an axis = V − 2 + E + 3E = 5E − F,
3. number of triangles = F + 3E.
Total number of corners, sides & triangles surrounding an axis = 10E − F.
The axis of the disdyakis triacontahedron (E = 180, F = 120) is surrounded by 1680 points, lines & triangles, whilst the axis of the 144 Polyhedron (E = 216, F = 144) is surrounded by 2016 points, lines & triangles, where 2016 = (6/5)×1680. What is special about the 144 Polyhedron is that any two of its populations of non-axial vertices, edges & faces are exactly 6/5 times their counterparts in the disdyakis triacontahedron. If they were not, their total populations would not be in this ratio. It must be emphasized that we do not need this property of the 144 Polyhedron in order to infer that the number of turns in the whorl of Cowen's particle has to be 2016 in order to maintain the analogy between the two types of whorl and the two polyhedra. This number could be inferred purely on the basis that the 144 Polyhedron should bear with the disdykis triacontahedron an analogy to the branches and trunk of the outer Tree and therefore must be 6/5 times whatever number the Cartan solid displayed as its population of geometrical elements. That the latter is precisely the number of turns counted by Leadbeater in a whorl of the UPA is striking evidence that the two polyhedra do, indeed, constitute the polyhedral form of the inner and outer forms of the Tree of Life in the subatomic world.
As concluded in earlier sections, a whorl of the UPA with 1680 turns is like the trunk of the Tree of Life, whilst a whorl in Cowen's particle is like the branches of the Tree of Life. The analogy therefore implies that the latter whorl should have (6/5)×1680 = 2016 turns, which in turn implies that 2016/6 = 336 turms are spread over each of its six revolutions. But this is the same for the UPA because 1680/5 = 336. The predicted number is the same as the number inferred from two pieces of purely observational data because the ratio of the number of revolutions of a whorl in the two particles (a number generated by pure observation) is exactly the proportion displayed by sacred geometries such as the Tree of Life and its polyhedral counterpart. One could dismiss this as coincidence. But a more reasonable reaction would be the inference that the number of turns per revolution of their whorls has to be the same for both particles because they constitute the trunk and branches of the microscopic realisation of the Tree of Life. The 1680 geometrical elements that surround an axis of the disdyakis triacontahedron are the counterpart of the 1680 turns in the UPA's whorl, whilst the 2016 geometrical elements surrounding an axis of the 144 Polyhedron are the counterpart of the 2016 turns predicted to be in a whorl of the particle described by Cowen, which the author interprets as an E8-singlet state of the E8×E8' heterotic superstring and as the basic constituent of dark matter.
Returning to the 1-tree, suppose that we assign the number 336 to each of its 80 yods. The 30 blue yods in the kite-shape with corners at Tiphareth, Netzach, Hod, Yesod & Malkuth denote the 30 revolutions in the five whorls in Cowen's particle and generate the number 30×336 = 10080, which is the number of their turns. The 50 red yods above the kite signify the 50 revolutions in the 10 whorls of the UPA and generate the number 50×336 = 16800, which is the number of their turns. Their total number of turns = 26880 = 80×336 = 2×10×22×22×(12+32+52+72) = 2×(1+2+3+4)×(42+122+202+282). Their inner or outer halves have in total 13440 turns, where
13440 = (1+2+3+4)(42+122+202+282).
This demonstrates the power of the Tetrad to determine arithmetically cosmic parameters such as the number of waves in the whorls of the two basic constituents of physical matter.
We now see how apt is the connection between the zelim and the Upper Face of the Tree representing Assiyah (coloured blue in the diagram showing the four Worlds). It is the same geometrical object as the lower kite-shape depicted in the 1-tree (coloured white), so it, too, has 30 yods. It embodies the number 10080, i.e., the number of waves that make up the basic particle composing the matter of the second universe, including the human zelim.
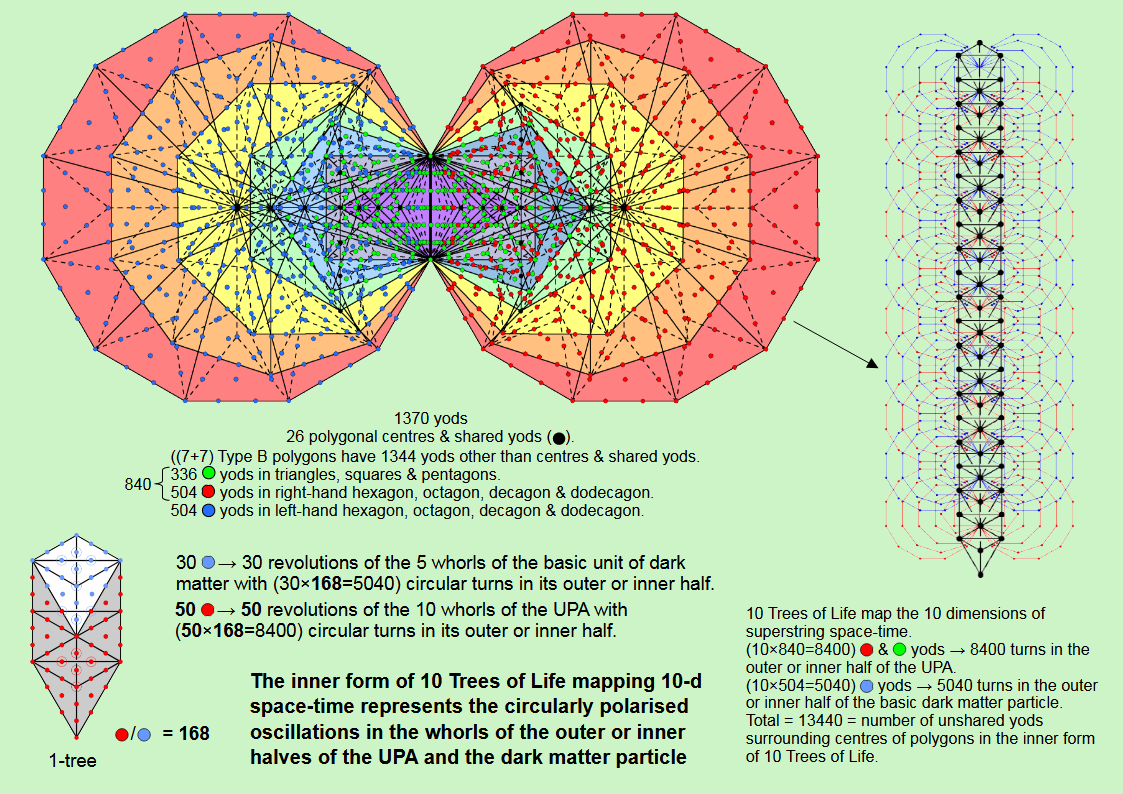
Suppose, instead, that we weight each of the 80 yods of the 1-tree with the gematria number value 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth. The kite-shape now generates the number 30×168=5040, which is the number of turns in the outer or inner halves of Cowen's particle, which the author has identified as the fundamental constituent of dark matter. The rest of the 1-tree generates the number 50×168 = 8400, which is the number of turns in the outer or inner halves of the UPA, identified by the author as the yet-to-be-discovered constituent of quarks. The 80 yods in the 1-tree generate the number 80×168 = 13440 = 10×1344. As the (7+7) enfolded Type A polygons of the inner Tree of Life comprise 94 triangles with 80 corners, we could generate this number just as well by assigning the weight 168 to each corner. However, their transformation into Type B polygons reveals a very remarkable property. The (7+7) polygons of the inner Tree of Life contain 524 yods when they are Type A and 1370 yods when they are Type B. This means that 520 yods in the former are outside the root edge, leaving 850 more yods, where 850 = (1+2+3+4)×85 and 85 = 40 + 41 + 42 + 43. The topmost corners of its two hexagons coincide with the lowest corners of the two hexagons belonging to the inner form of the next higher Tree of Life. This means that 1368 yods are intrinsic to the inner form of each Tree, so that the number of yods in the inner form of the n-tree = 1368n +2, where "2" denotes the topmost corners of the two hexagons belonging to the inner form of the nth Tree. The seven yods that line the vertical line joining the two shared, opposite corners of each hexagon are shared with the nth Tree. (6n+1) such yods line each side pillar of the n-tree. They contain the centres of the two hexagons in each set of 7+7) enfolded polygons. Hence, the number of centres and shared yods in the n-tree = 2×(6n+1) + 2×6n = 24n + 2. The number of unshared yods in the inner form of the n-tree that surround centres = 1368n + 2 − (24n+2) = 1344n. Associated with each half of this inner form are 672n. Outside the root edges are 670n such yods, where 670 = 67×10 and 67 is the number value of Binah. The pair of Type B triangles, squares & pentagon have 336 unshared green yods surrounding their centres (168 yods associated with each set), leaving (1344−336=1008) unshared yods surrounding centres of the hexagons, octagons, decagons & dodecagon, each set of four polygons having 504 such yods (red/blue). There are (336+504=840) red & green yods and 504 blue yods. For the 10-tree, which maps the 10 dimensions of the space-time of superstrings, its inner form comprises 140 polygons, where 140 is the number value of Masloth, the Mundane Chakra of Chokmah. There are (10×10=100) polygons containing 8400 red & green yods and 40 polygons containing 5040 blue yods, a total of 13440 unshared yods that surround the 140 centres of polygons. With Type B polygons, the inner form of 10 Trees of Life represents the 13440 circularly polarised waves in an outer or inner half of both the UPA (8400 waves) and the basic particle of dark matter (5040 waves).
The number of unshared yods or centres in the n-tree = 24n + 2. The 1-tree has 26 such yods, where 26 is the number value of YAHWEH, the Godname of Chokmah. The 10-tree has 240 of these yods that belong exclusively to it, 120 yods being on either side of the central Pillar of Equilibrium. As
120 = 4×30 = 22(12+22+32+42) = 22 + 42 + 62 + 82,
this demonstrates how the Tetrad determines both the shared yods and centres, as well as the 1344 unshared yods surrounding centres of the (7+7) polygons in the inner form of each Tree, where 1344 = 42 +122 + 202 + 282.
The superstring meaning of the 240 yods is provided by the following remarkable analogy with the 421 polytope. This 8-d polytope has 240 vertices, 6720 edges and 9×6720 triangular faces, as well as higher-dimensional cells that need not be described here. If we imagine its faces turned into tetractyses, there are 2×6720 hexagonal yods lining their sides. This demonstrates how this polytope is the polytopic counterpart of the inner form of 10 Trees of Life representing the 10 Sephiroth, for — just as 240 corners of tetractyses (120 in each half) and 6720 pairs of hexagonal yods line the edges of the 421 polytope, giving it its shape — so this inner form comprises 240 centres or unshared yods (120 in each half) and 6720 pairs of yods (6720 yods in one half and their 6720 mirror images in the other half). If one imagines a straight line joining each pair, the 6720 such lines are analogous to the 6720 edges of the 421 polytope, in particular, the 6720 lines joining pairs of hexagonal yods in all the edges. The vertices of the polytope represent the 240 roots of E8, the 8-d exceptional Lie group that describes the unified symmetries of the E8-singlet and E8'-singlet states of the E8×E8' heterotic superstring, among which, according to the author, are, respectively, the particle described by Ron Cowen and the UPA described by Besant & Leadbeater.
The 3360 yods in the 10 pairs of Type B triangles, the 10 pairs of Type B squares and the 10 pairs of Type B pentagons signifiy the difference:
8400 − 5040 = 3360
between the number of waves in either half of the UPA and the number of waves in either half of the basic dark matter particle. Notice the correspondence between the numbers of corners in the four sets of polygons in the inner form of each Tree and the number of yods contained in each set:
|
Set of polygons |
dodecagon+decagon +octagon+hexagon |
pentagon+square+triangle |
pentagon+square+triangle | dodecagon+decagon +octagon+hexagon |
| Number of corners |
36 = 3×12 |
1×12 |
1×12 |
36 = 3×12 |
|
Number of yods |
3×168 = 36×14 |
1×168 = 12×14 |
1×168 = 12×14 |
3×168 = 36×14 |
Remarkably, a Type B dodecagon has 168 yods surrounding its centre other than its corners. The same yod populations are obtained by assigning the number 14 to each corner of the set of 14 separate polygons! In fact, as the yod population of the Type B n-gon = 15n + 1, the total number of yods in each set of enfolded Type B polygons is the numbers of yods other than their corners that surround their centres: ∑14n = (36 or 12)×14. Indeed, as the number of hexagonal yods in the Type A n-gon = 5n, the total number of such yods in the seven polygons with 48 corners when they are Type A = ∑5n = 5×48 = 240. This is the number of centres or unshared yods in the 140 polygons making up the inner form of the 10-tree! The factorisation of 672 as 48×14 appears explicitly in the inner form of the Tree of Life because the Type C polygon has 14 sides of nine triangles per sector, so that the triangles in the seven Type C polygons with 48 sectors have (48×14=672) sides. This means that the inner form of 10 Trees of Life contains 6720 sides of triangles in each set of 70 polygons when they are Type C, i.e., 13440 sides in total, and these sides correspond to the 6720 edges of the 421 polytope (for more details, see here). Here is remarkable evidence that the 421 polytope is the polytopic version of the inner form of 10 Trees of Life.
The numbers 168, 336 & 504 reappear in single polygons. As the Type C n-gon has 42n yods surrounding its centre, the Type C square has 4×42=168 such yods, the Type C octagon has 8×42=336 yods (see here) and the Type C dodecagon has 12×42=504 yods. As the Type C n-gon has 28n geometrical elements surrounding its centre, the Type C dodecagon has 12×48=336 corners, sides & triangle (see here).
The number of corners & sides of the 3n triangles surrounding the centre of the Type B n-gon = 7n. Surrounding the centres of the seven Type B polygons are (48×7=336) corners & sides of (48×3=144) triangles. Surrounding the centres of the 14 separate Type B polygons making up the inner form of each Tree are (2×336=672) corners & sides of 288 triangles. There are 6720 corners & sides for the 10-tree (see here).
| << Previous 1... 18 19 [20] 21 22 ...24 Next >> |