| << Previous 1... 19 20 [21] 22 23 ...24 Next >> |
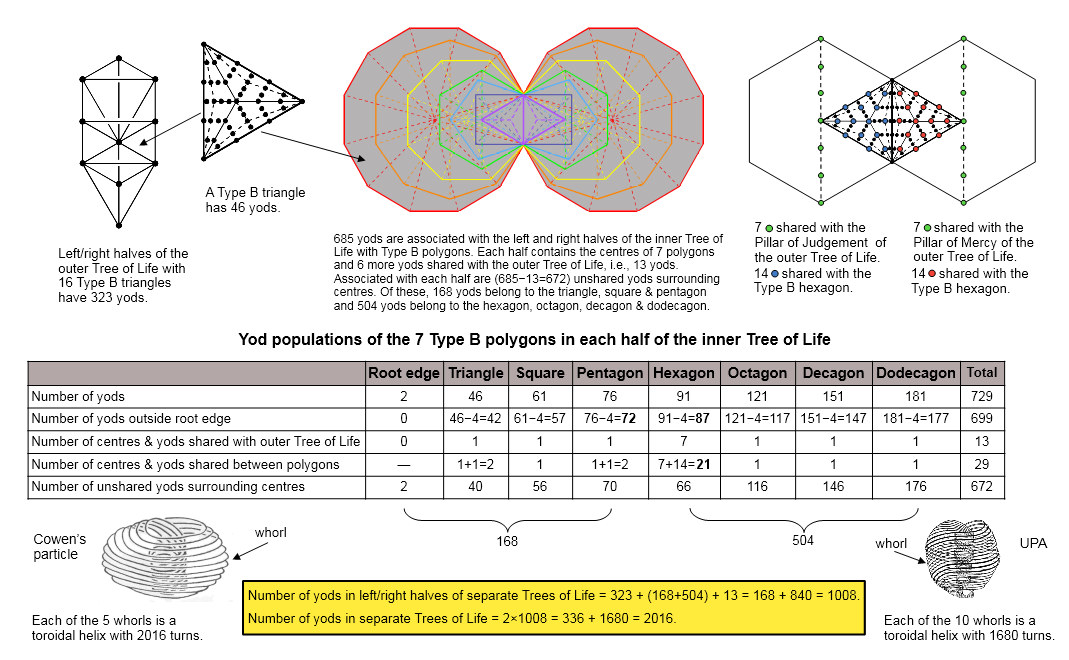
#21 The outer & inner Trees of Life with Type B polygons embody the superstring structural parameters 1680 and 2016

The Type B n-gon has (15n+1) yods. The Type B triangle (n = 3) contains 46 yods, nine yods lining its sides and 37 yods inside it. The outer Tree of Life is constructed from 16 triangles with 22 sides and 10 corners. (22×2=44) hexagonal yods line its sides, i.e., (10+44=54) yods in total. Inside each Type B triangle are (16×37=592) yods. The total number of yods in the outer Tree of Life with Type B triangles = 54 + 592 = 646. The 16 triangles consist of six triangles with horizontal bases (three upper ones and their three lower, congruous counterparts) and 10 inclined triangles (five on one side of the central axis of the Pillar of Equilibrium and their mirror images on its other side). This means that the outer Tree is made up of two sets of eight triangles, each defining a "half". It cannot be divided into two geometric halves that are mirror images of each other because the set of six triangles span both such halves. This necessitates a choice to be made about which yods aligned with the Pillar of Equilibrium should be associated with each suitably-defined half. Let them be assigned to the right half if they belong to the upper set of three triangles with horizontal bases and to the left half if they belong to the lower three triangles with horizontal bases. This is just a convention that makes no difference to the calculated yod population of either half — however this word is defined — because to every triangle in the upper set of three there corresponds a congruent triangle in the lower set. The definition of the two halves is completed by assigning to the left half one of the two hexagonal yods that lie on any vertical side aligned with the central pillar and by assigning to the right half the other hexagonal yod. In this way, (646/2=323) yods can now be regarded as making up each half of the outer Tree of Life with Type B triangles. The number of yods (apart from the 10 Sephirothic corners) that are needed to construct both halves of the outer Tree of Life = 646 − 10 = 636, where 636 is the gematria number value of Rashith ha Gilgalim ("First Swirlings"), the Kabbalistic name of the Mundane Chakra of Kether.
Being mirror images of each other, the two sets of seven enfolded polygons in the inner Tree of Life pose no problem for defining the two halves of the inner Tree of Life. We may, simply, associate two of the four yods lining the root edge shared by all 14 polygons with one set and the two other yods with the other set. When they are Type B, the 14 enfolded polygons have 1370 yods. Either half contains 685 yods. The seven yods (coloured green in the diagram shown above) that line the vertical line connecting the top and bottom corners of each hexagon are shared with the outer Tree constructed from Type B triangles. One of them is its centre. Therefore, (7+6=13) yods are either shared or centres of polygons. Each of the two Type B triangles occupies one of the Type A sectors of each hexagon. This means that, as illustrated in the diagram, 14 yods (coloured red) in each triangle, as well as its green corner, coincide with yods in each Type B hexagon. It has 91 yods (87 outside the root edge, where 87 is the number value of Levanah, the Mundane Chakra of Yesod, and (87−7−14=66) yods that are intrinsic to it, being unshared with either the outer Tree or the triangle occupying one of the sectors of the hexagon.
The table in the diagram shows that, together with the 13 yods in each set of seven enfolded polygons that are either centres or shared with the outer Tree, there are 168 yods in the first three polygons and 504 yods in the last four polygons, totalling 685 yods in each half of the inner Tree of Life. The number of yods in either the left-hand or right-hand halves of the separate outer and inner Trees = 323 + 168 + 504 + 13 = 168 + (323+13) + 504 = 168 + 840 = 1008. The separate outer and inner Trees have (2×1008=2016) yods. They comprise:
Compare the yod populations 1680 and 2016 with the number of circular turns in a whorl of the particles described by Ron Cowen, Annie Besant and C.W. Leadbeater. Each of the five whorls in the former is a toroidal helix with 2016 circular turns (1008 in an outer or inner half). Each of the 10 whorls in the latter is a toroidal helix with 1680 circular turns (840 in an outer or inner half). The yod population of the separate outer and inner Trees of Life is 2016. We see that each yod symbolises a turn (a circularly polarised oscillation) in each whorl of Cowen's particle. The 1008 yods in their left-hand or right-hand halves denote the 1008 turns in its outer or inner halves. The outer Tree and the (13+13=26) centres/shared yods comprise (672=2×336) yods; the last (4+4) polygons contain (1008=3×336) yods, totalling (1680=5×336) yods. This confirms Leadbeater's count of 1680 turns in each whorl of the UPA. The (168+168=336) yods in the first (4+4) polygons denote the extra 336 turns in each whorl of Cowen's particle. As he reported that each whorl makes six, not five, revolutions around the axis of spin of the particle, the explicit presence of 336 yods in some of these polygons making the difference between the numbers 1680 and 2016 is striking confirmation of the author's conclusion (based upon analysis of how several isomorphic sacred geometries embed these numbers) that there are 336 turns per revolution of a whorl, whether it belongs to the UPA or to Cowen's particle.
The sceptic may argue that it might be just coincidence that the yod population of the separate outer & inner forms of the Tree of Life is the number of turns in a whorl of Cowen's particle, which the author has independently predicted. But how likely is it that this population should yield — also by chance — the very number that was counted in the UPA by Leadbeater? Any reasonable person should reject the possibility of occurrance of two such coincidences as highly improbable. Instead, this property is remarkable evidence that the Tree of Life is a blueprint of the "image of God" in matter, namely, the E8×E8' heterotic superstring, Cowen's particle belonging to the E8-singlet sector of this symmetry group and the UPA belonging to its E8'-singlet sector.
The square is a symbol of the number 4. It provides a geometrical representation of the division:
2016 = 336 + 1680
present in the separate outer and inner Trees of Life, as now explained. As
336 = 4×84
and
1680 = 5×336 = 4×5×84,
2016 = 4×84 + 4×5×84 = 4(1+5)×84.
The Type A square is a square whose sectors are tetractyses. The six yods per sector consist of one corner and five hexagonal yods. The 24 yods surrounding its centre consist of its four corners and (4×5=20) hexagonal yods. Weighted with the number 84, the former generates the number (4×84=336) and the latter generates the number (20×84=1680). As
84 = 12 + 32 + 52 + 72,
the square provides a representation of this number as well:
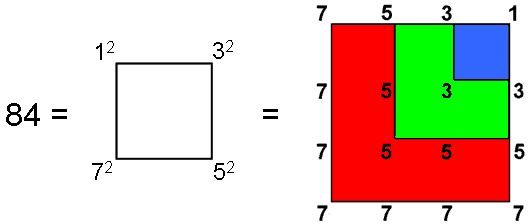
Even its superstring meaning refers to a four-fold division of a circle, for the number 336 is the number of turns of a helical whorl in each revolution around the axis of the UPA, which means that every ¼-revolution contains 84 turns (see #18).
The four-fold, geometrical patterns of numbers determining the superstring structural parameters 336, 1680 and 2016 are examples of the Tetrad Principle proposed by the author in his Article 1. As pointed out on #14, there are 336 yods surrounding the centre of a cross pattée whose four arms are 2nd-order tetractyses, each with 85 yods, where
85 = 40 + 41 + 42 + 43.
This four-fold, geometrical representation is another illustration of how the superstring structural parameter 336 conforms to the Tetrad Principle.
When the outer and inner Trees of Life with Type B polygons are combined, the seven yods lining each side pillar coincide with the seven yods lining the two vertical sides inside each hexagon, whilst the two hexagonal yods on the straight line joining Chesed and Geburah coincide with the centres of the two triangles in the inner Tree of Life. Combining the outer and inner forms causes sixteen yods to disappear, so that the new yod population is
646 + 1370 − 2 − 7 − 7 = 2000.
Associated with each half of the combined Trees of Life are 1000 yods, where
1000 = 103 = (1+2+3+4)3 = (1+2+3+4)(13+23+33+43).
The number of yods unshared between the outer and inner Trees when combined = 2000 − 16 = 1984, where
1984 = 4×496 = 4(13+33+53+73),
and 496 is the number value of Malkuth, the tenth Sephirah of the outer Tree of Life.
Quite apart from this property being further illustration of the power of the Tetrad to express properties of the Tree of Life, the remarkable appearance of the superstring dynamical parameter 496 as the dimension of E8×E8' cannot be regarded as coincidental, given that the two predicted structural parameters 1680 and 2016 of the E8×E8' heterotic superstring appear in the yod population of the separate Trees of Life. Rather, it is undeniable evidence of beautiful, mathematical design. The dimension 248 of E8 appears as well as a geometrical parameter of the separate outer and inner Trees of Life, as now shown. Each of the 16 Type B triangles of the outer form of the Tree of Life consists of nine tetractyses with four internal corners, so that the total number of corners of the (9×16=144) tetractyses = 10 + 16×4 = 74. The 94 sectors of the (7+7) enfolded polygons have 80 corners, where 80 is the number of Yesod. Each Type A sector has one internal corner shared by three tetractyses, so that the total number of corners of the (3×94=282) tetractyses making up the (7+7) enfolded polygons = 80 + 94 = 174. The number of corners of the (144+282=426) tetractyses in the separate outer and inner Trees of Life = 74 + 174 = 248. This is both the number value of Raziel, the Archangel assigned to Binah, and the dimension of the Lie group E8. The square also embodies this number because 248 yods surround the centre of a square whose sectors are 2nd-order tetractyses (see #18).
The number of hexagonal yods either at the centres of the 144 tetractyses in the outer Tree of Life or at the centres of the 282 tetractyses in its inner form = 144 + 282 = 426. As we found above, the combined Trees have 2000 yods, so that (2000-426=1574) yods line these tetractyses. They include:
The number of yods that are unshared between the outer and inner Trees and include all those yods in the inner Tree that surround the centres of their polygons = 1574 − 1 − 7 − 1 − 7 − 4 − 4 = 1550 = 10×155, i.e., it is the number of yods in 155 tetractyses. The number 155 is the number value of ADONAI MELEKH, the complete Godname of Malkuth, which has the pentagramic representation:
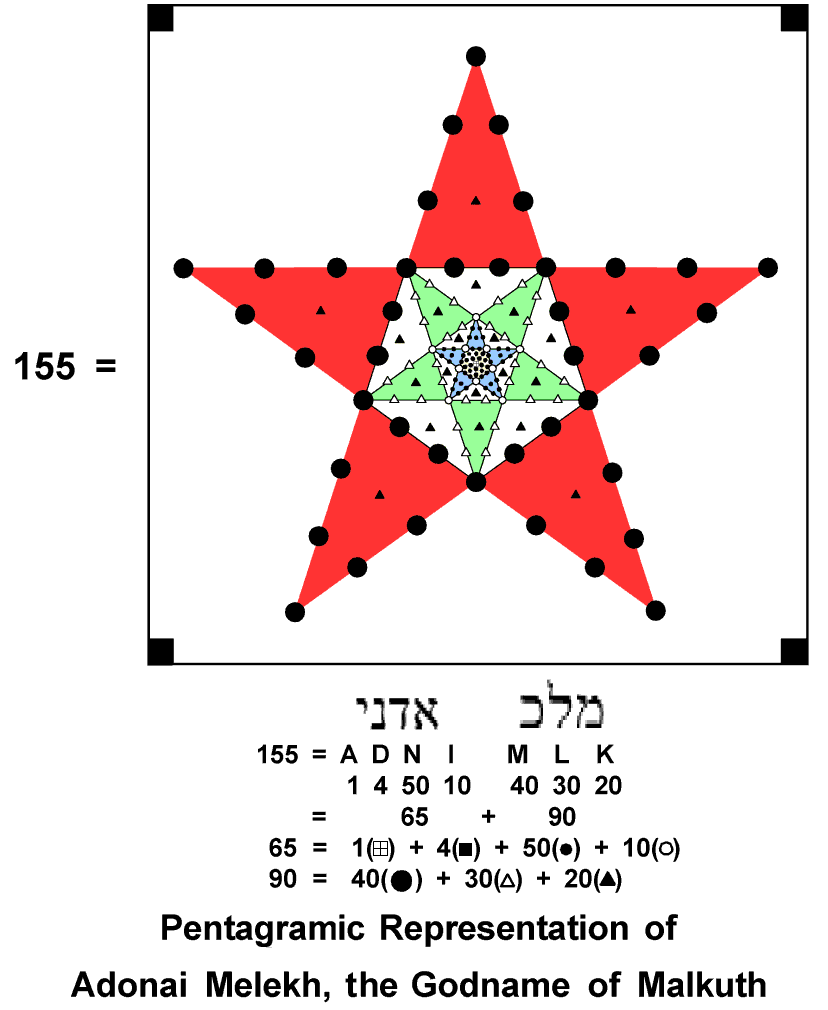
The gematria number values of the letters of the Divine Name are the numbers of various classes of yods present in the representation. This remarkable property shows how the Godname of the Sephirah signifying the material form, or body, of any system constructed according to the blueprint of the Tree of Life prescribes the number of unshared yods in the combined Trees that delineate their shapes because they are located at points on boundaries of tetractyses outside centres of polygons.
Of the 1574 yods lining tetractyses in the combined Trees of Life, (1+7=8) yods in each half are shared. The number of unshared yods outside the root edge = 1574 − 8 − 8 − 4 = 1554. There are (1554/2=777) boundary yods outside the root edge in each half, where
777 = ¼(14 + 34 + 54 + 74),
i.e., it is the arithmetic mean of the fourth powers of the first four odd integers. Here is further, striking evidence of the Tetrad Principle at work in expressing global parameters of the Tree of Life. As 777 = 21×37, where 37 is the number of yods either lining the sides of a hexagram or at its centre, this number has the following representation:
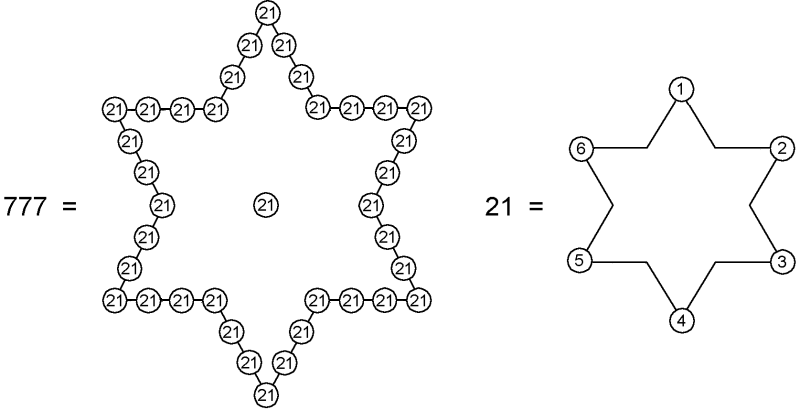
The number value 21 of EHYEH (AHIH, "I am"), the Godname of Kether, can also be represented by the first six integers assigned to the corners of a hexagram. Notice that the number 1 denotes the gematria number of A (alef), the sum: 2 + 3 = 5 denotes the number of H (he), the sum: 4 + 6 = 10 denotes the number of I (yod) and the number 5 denotes the number of the second letter H. In #17 we found an analogous representation by a hexagram of the geometrical composition of the combined Trees of Life with Type B polygons. Both illustrate the mathematical potency of the hexagram for expressing various structural parameters of the Tree of Life.
In conclusion, when composed of Type B polygons, the separate outer and inner Trees of Life embody:
1. the independently predicted number of turns in each of the five toroidal helices making up
the basic particle that was reported by Ronald Cowen in his book "The Path of Love" to constitute the invisible
matter that he and other clairvoyants have claimed permeates the human body. The author has identified the particle
as an E8-singlet state of the E8×E8' heterotic superstring;
2. the number of turns counted by Leadbeater in each of the 10 toroidal helices that form the basic constituent of
nuclear matter, a particle that the author has proved in his books to be a yet-to-be-discovered constituent of the
quarks making up protons and neutrons;
3. the dimension 248 of E8 and E8' and the dimension
496 of E8×E8′.
Any suggestion that the numbers 1680 and 2016 predicted by the author to be relevant to the physics of E8×E8' heterotic superstings could be both embodied by chance in the outer and inner Trees of Life is made highly implausible by the additional presence of the numbers 248 and 496 measuring their various yod populations when the Trees are either separate or combined.
| << Previous 1... 19 20 [21] 22 23 ...24 Next >> |