#8 The I Ching connection

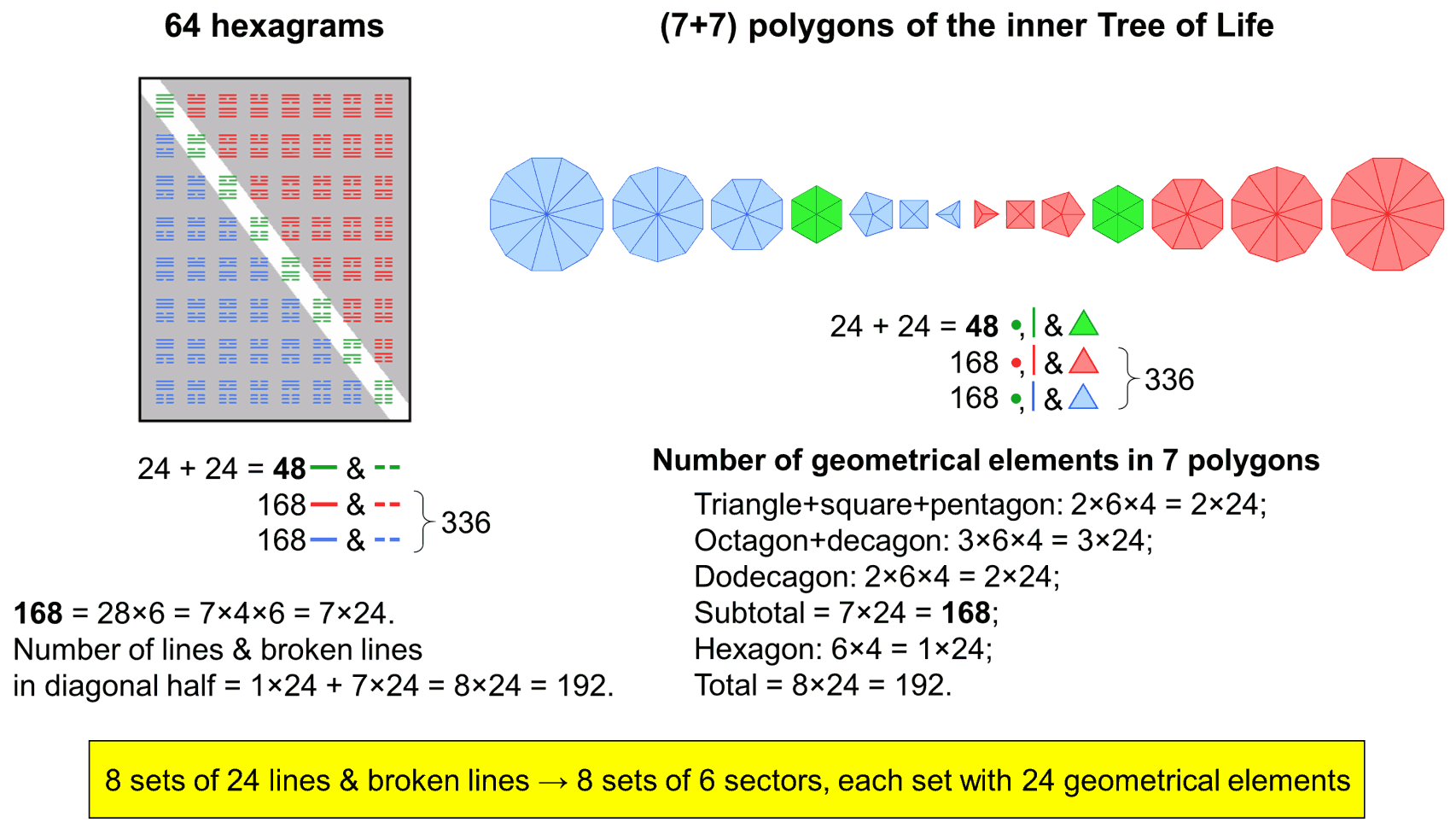
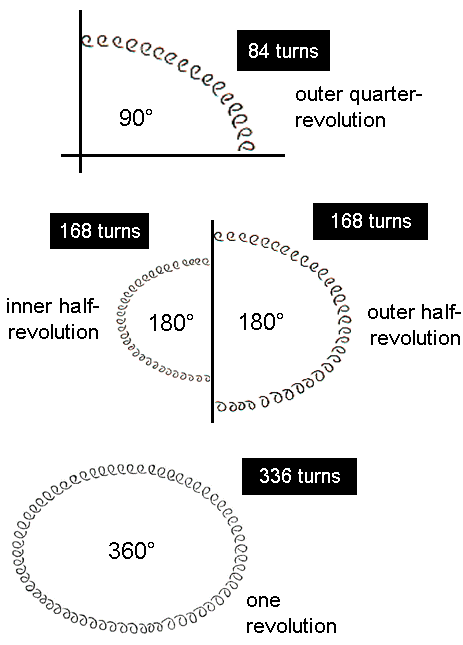
We have seen that the 48 sectors of the seven polygons exhibit a (3+3=6)×8 pattern, where "(3+3)" denotes the three outer revolutions of the shadow matter whorl and its three inner revolutions and where "8" denotes the eight E₈′ gauge charges per revolution made up of 336 turns. Each half-revolution of 168 turns contains four charges. The (30+30=60) half-revolutions of the five whorls express the (120+120=240) charges spread over the outer and inner spirals of the five whorls of the shadow matter particle. The Coxeter plane projection of the 240 vertices of the 4₂₁ polytope exhibits the same division of vertices because they become the corners of two sets of four triacontagons (see here), the triacontagon with 30 corners being the Petrie polygon for this polytope. Indeed, one may speculate here whether the 30 revolutions of the five whorls, each carrying eight E₈′ gauge charges, are a manifestation in space-time of the 30 sets of eight vertices that can be defined when one corner of each triacontagon make up such a set. The five whorls, each carrying 48 gauge charges, would then correspond to dividing each triacontagon into five hexagons, creating sets of (6×4×2=6×8=48) charges per hexagon and leading to the physically-realised factorisation of the number 240 as 5×6×4×2. This is the pattern of hexagonal yods in the seven separate Type A polygons when their two "halves" are divided into sets of six sectors:

triangle+square+pentagon: 12 = 6×2;
dodecagon: 12 = 6×2;
Subtotal for 1st half = 6×(2+2=4);
hexagon: 6 = 6×1;
octagon+decagon: 18 = 6×3;
Subtotal for 2nd half = 6×(1+3=4);
Total = 6×4×2.

5 hexagonal yods per sector×24 sectors per half×2 halves = 240 hexagonal yods in 7 polygons.

An outer half-revolution would be the manifestation of one gauge charge associated with a corner from each of the four triacontagons whose 120 corners are the projection of the 120 vertices of a 600-cell; an inner half-revolution over which are spread four gauge charges would be associated with four corners of the second set of four triacontagons that are the projection of a smaller 600-cell inside the first one. Support for this speculation comes from the 8×8 square array of 64 hexagrams used in the ancient Chinese system of divination known as "I Ching" (see here). Its isomorphism with other sacred geometries has been demonstrated elsewhere on this website (see here). Analogous features of the inner Tree of Life are now summarised. Each successive sector of a polygon has a corner, an outer side, an inner side and a triangular area, i.e., four geometrical elements. The seven polygons in each half of the inner Tree of Life have 48 sectors with (48×4=192) geometrical elements surrounding their centres. Both halves have (192+192=384) geometrical elements surrounding their 14 centres. This compares with the (64×6=384) lines & broken lines making up the 64 hexagrams:

The 384 lines & broken lines in the 64 hexagrams correspond to the 384 geometrical elements surrounding the centres of the (7+7) polygons of the inner Tree of Life. On either side of the diagonal of eight hexagrams with 48 lines & broken lines are 28 hexagrams with 168 lines & broken lines. Their counterparts in the inner Tree of Life are the 48 geometrical elements surrounding the centres of the two hexagons and the 168 geometrical elements surrounding the centres of the remaining six polygons in each half of the inner Tree of Life.

The 168 turns in each half-revolution of a whorl correspond to the 168 lines & broken lines in the 28 off-diagonal hexagrams in each diagonal half of the 8×8 array of 64 hexagrams.

The diagonal of the square array comprises two sets of eight trigrams. As there are 16 sets of eight trigrams, there are 14 sets of off-diagonal trigrams. The seven sets in each half comprise (7×8×3=168) lines & broken lines (84 lines & 84 broken lines). The 48 sectors in each half of the inner Tree of Life consist of the six sectors of the hexagon and 42 sectors of the six other polygons. As shown in the diagram, they form eight sets of six sectors, each set having (6×4=24) geometrical elements surrounding centres of polygons. For example, the dodecagon has 12 sectors, where 12 = 2×6, and the octagon and decagon have 18 sectors, where 18 = 3×6. These eight sets are the geometrical counterpart of the eight sets of eight trigrams, each set having 24 lines & broken lines, that make up each half of the square array of 64 hexagrams. A hexagon is the counterpart of the eight trigrams making up either half of the eight diagonal hexagrams. The six other polygons in each half of the inner Tree of Life consist of seven sets of six sectors, each with 24 geometrical elements; they correspond to the seven sets of eight trigrams, each composed of 24 lines & broken lines. The 336 turns in a revolution of a whorl are the string manifestation of both the 336 lines & broken lines in the 56 off-diagonal hexagrams and the 336 geometrical elements in the 12 polygons other than the two hexagons. Just as the 336 turns carry 48 E₈′ gauge charges (24 in an outer or inner half-revolution), so the eight diagonal hexagrams have (24+24=48) lines & broken lines, whilst the two hexagons have (24+24=48) geometrical elements surrounding their centres. One gauge charge is spread over 1/8th of a complete revolution of a whorl.

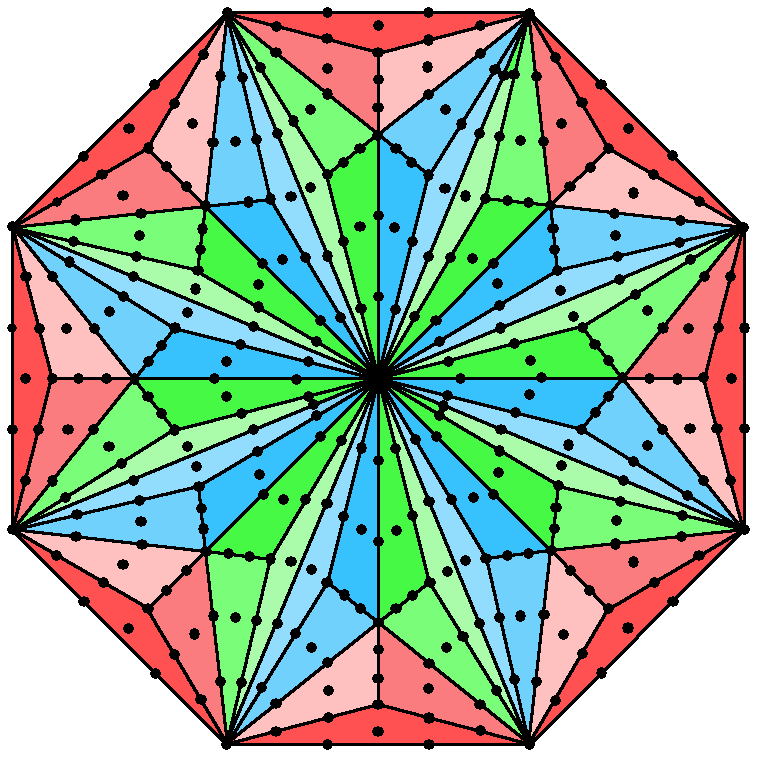
This eight-fold aspect of every revolution of a whorl of the shadow matter particle is embodied in a single Type C octagon as the 336 yods surrounding its centre:

The Type C octagon embodies the structural parameter 336 of the shadow matter superstring.

Each yod symbolises a turn of the whorl; each sector with 42 yods represents an E₈′ gauge charge spread along 42 turns, i.e., this octagon represents the eight such charges spread along each of the 30 revolutions of the whorls making up the shadow matter superstring. As a Type A n-gon is isomorphic to n Trees of Life up to the level of Chesed of the nth Tree as far as their yods and SLs are concerned, it should come as no surprise that the number 336 is embodied in the 8-tree, as now explained. The number of yods in the n-tree constructed from tetractyses is:

Y(n) = 50n + 30,

where 50 is the number value of ELOHIM, the Divine Name assigned to Binah. As there are 32 yods above Chesed in the nth Tree, the number of yods up to this Chesed is:

Ý(n) = Y(n) − 32 = 50n − 2.

Chesed of the eighth Tree is the 49th SL, where 49 is the number value of EL CHAI, the Godname assigned to Yesod. There are Ý(8) = 398 yods up this SL There are Y(7) = 380 yods in the 7-tree. Two yods outside it lie below its apex on either side. There are 384 yods up to the top of the 7-tree that maps the physical plane. They correspond to the 384 lines & broken lines in the 64 hexagrams and to the 384 points, lines & triangles that surround the 14 centres of the polygons in the inner Tree of Life. Including the latter, the 398 geometrical elements correspond to the 398 yods up to Chesed of the eighth Tree:

The 384 yods up to the top of the 7-tree mapping the physical plane correspond to the 384 geometrical elements surrounding the 14 centres of the polygons of the inner Tree of Life. The latter correspond to the 14 green yods above the top of the 7-tree as far as Chesed of the 8th Tree of Life.

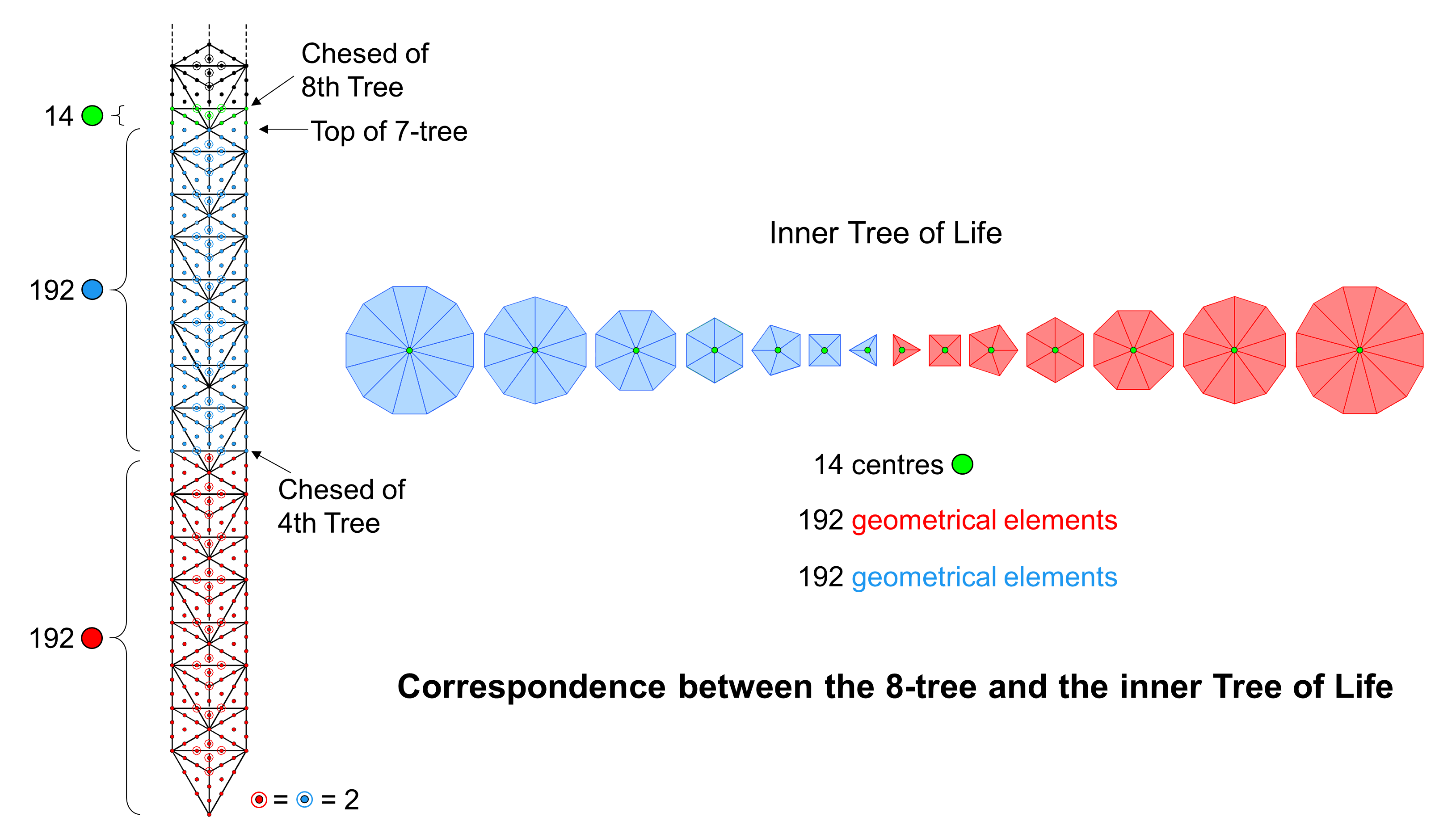As well as mapping subplanes, Trees of Life can represent dimensions of space. ADONAI, the Godname of Malkuth with number value 65, specifies the 65 SLs in the lowest 10 Trees that map the 10 spatial dimensions required by M-theory (indeed, its letter values denote different sets of SLs in the 10-tree — see here). Embodied in the 10-tree are 496 yods that symbolise the 496 gauge fields of the symmetry groups SO(32) & E₈×E₈′ that are free of quantum anomalies (see here). The number 496 is the number value of Malkuth. ADONAI MELEKH, the complete Godname of this Sephirah, has the number value 155 that specifies the 155 SLs in the lowest 25 Trees mapping the 25 dimensions of space predicted by bosonic string theory. Here, the 8-tree maps the eight dimensions of space that are transverse to the direction along which the string extends. The two large-scale dimensions define the plane containing each of the 336 circularly polarised oscillations made by a whorl during one revolution about the axis of the shadow matter superstring and the six compactified dimensions generate as circles the six higher orders of spirillae in each whorl. This cycle is divided into eight equal parts, each of 42 oscillations. One is reminded of how in Taoism the eight trigrams are sometimes represented in a circle, indicative of their constituting the eight phases of a complete cycle:

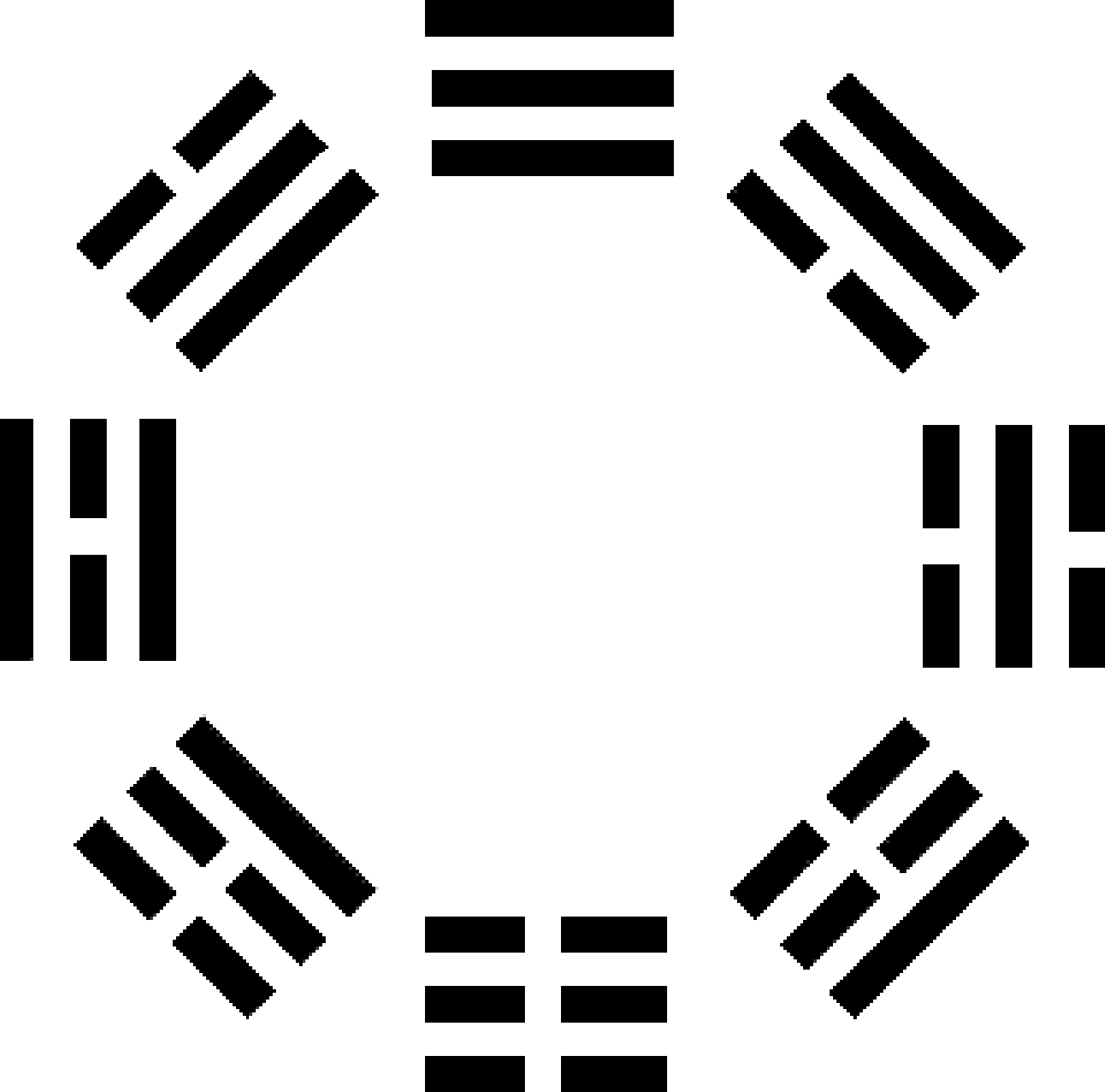
The number 8 measures the eightfold, cyclic nature of holistic systems, whether they be the eight notes of the musical octave, the eight diatonic musical scales known as the eight Church Modes, or the eight groups of the Periodic Table of elements. The number 48 of Kokab, the Mundane Chakra of Hod, which is the eighth Sephirah of the Tree of Life, quantifies this cyclic character in the Tree of Life because every eight Trees have 8×6=48) SLs, whilst their inner form consists of (8×7=56) polygons with (8×48=384) cormers (280 when enfolded, where 280 is the number value of Sandalphon, the Archangel of Malkuth). This pattern corresponds precisely to the (8×48=384) lines & broken lines in the eight sets of eight hexagrams, each set having (8×6=48) lines & broken lines.

<< Previous    1...   6  7  [8]  9  10  ...20    Next >>

Home