| << Previous 1... 7 8 [9] 10 11 ...24 Next >> |
#9 The Sri Yantra connection
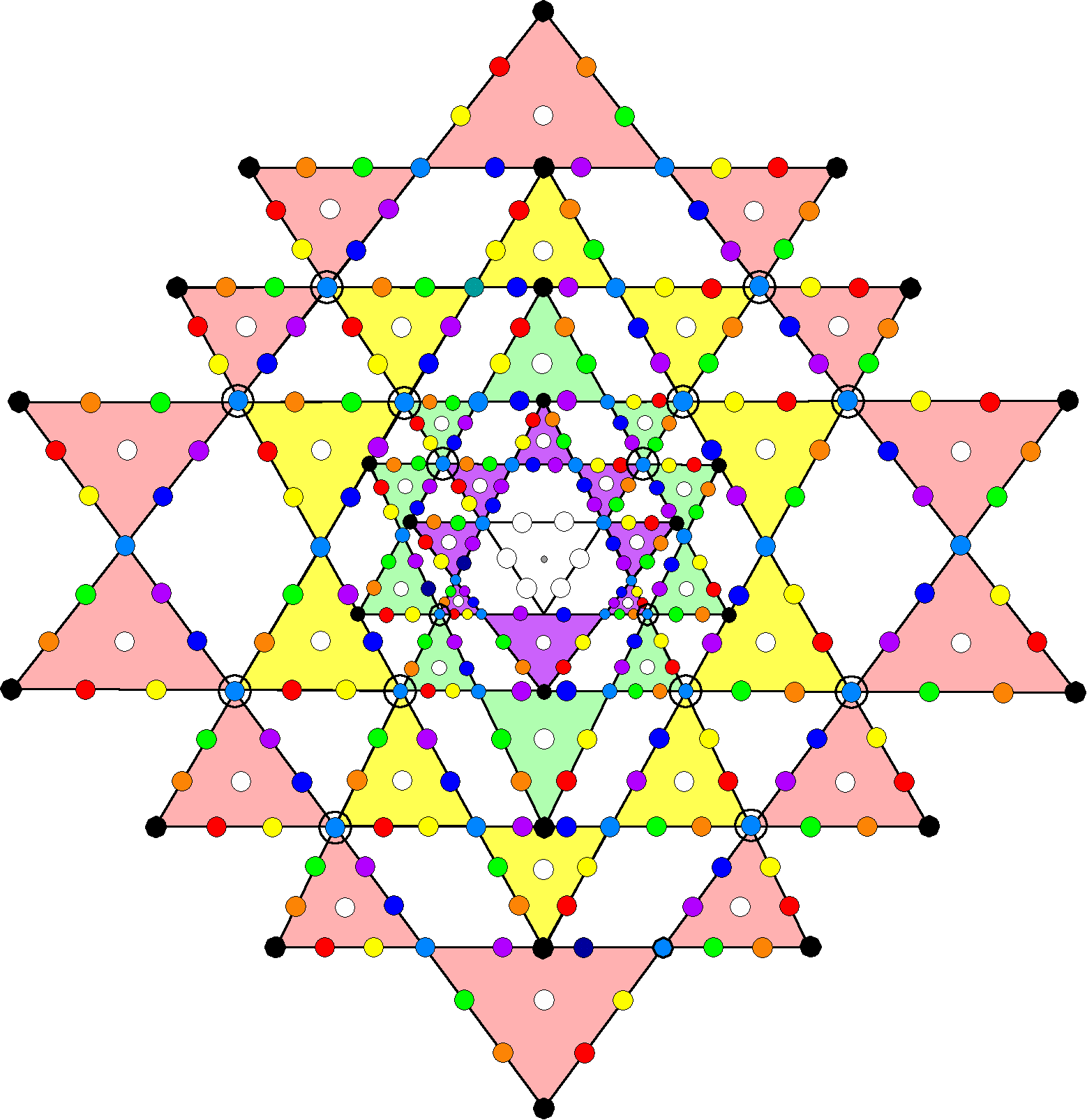
The eightfold division of the holistic parameter 336 as 8×42 appears as well in the 3-d Sri Yantra. This is necessarily the case because all holistic systems are isomorphic and therefore must display the same patterns of numbers in their structures. When the 42 triangles surrounding the central one are turned into tetractyses, their 126 sides are lined by 336 yods because nine yods line each tetractys, which are linked together in four layers, so that there are eight yods per triangle, and 42×8 = 336. This property is not shared by the 2-d Sri Yantra, in some of whose triangles the tip coincides with a corner shared by two triangles. Discussion is therefore confined to the 3-d Sri Yantra. The tips of triangles in the diagram show below are coloured black and the seven remaining yods lining tetractyses are assigned the seven prismatic colours:
 |
| Turned into tetractyses, the 42 triangles in the 3-d Sri Yantra that surround the central triangle are lined by 336 yods. The 42 copies of the eight differently coloured yods per tetractys represent the 42 circular turns carrying each of the eight E8′ gauge charges that are spread over every revolution of a helical whorl in the basic shadow matter particle. Black circles denote tips of triangles in a layer that lies directly above a corner shared by two triangles in the next lower layer. |
There are (21+21=42) white hexagonal yods at the centres of tetractyses and six white hexagonal yods (two triads) lining the central triangle. In the case of the inner Tree of Life, these 48 yods are analogous to the (24+24=48) geometrical elements in the two hexagons, either of which comprises three corners 120° apart and 21 other geometrical elements. The eight yods per triangle lining its sides comprise three pairs of hexagonal yods and two corners, i.e., four pairs of yods, which can be regarded as two sets of four yods (three hexagonal yods and one corner); this generates the factorisation: 336 = 2×21×2×4. The 2×4 factor is the counterpart of the basic set of eight trigrams, in which the last four trigrams are the result of the reversal in the first four of yang and yin polarities associated with the unbroken lines and broken lines. The 2×21 factor is the counterpart of the (7×3=21) rows in the seven basic sets of off-diagonal trigrams in either diagonal half of the 8×8 array of hexagrams. The counterpart in the inner Tree of Life of the seven sets of (4+4) trigrams with 168 lines & broken lines in each diagonal half of the 64 hexagrams is as follows: the six types of polygons other than the hexagon form two unique groups, each of which has 21 sectors:
triangle+octagon+decagon → (21×4=84) geometrical elements
square+pentagon+dodecagon → (21×4=84) geometrical elements
Total = 21×2×4 = 168 geometrical elements.
The 12 polygons other than hexagons in the two halves of the inner Tree of Life have 336 geometrical elements, where 336 = 2×168 = 2×21×2×4. As found above, this is the factorisation displayed by the 336 yods that line the 3-d Sri Yantra and by the 336 lines & broken lines making up the 112 off-diagonal trigrams in the 64 hexagrams. The (4+4=8) geometrical elements in each of the 21 pairs of corresponding sectors in the 12 polygons correspond to the (4+4=8) yods per triangle and to the 4:4 division iof the eight types of trigrams. This factorisation, which is common to sacred geometries, manifests in space-time as the 42 turns along which are spread each one of the four E8′ gauge charges in every half-revolution of a helical whorl of the shadow matter particle. Just as there are 42 copies of each one of the eight yods per triangle in the 3-d Sri Yantra, so, too, 42 turns are associated with each of the eight gauge charges spread along each revolution of a whorl. The pattern of 24 charges in an outer or inner half-revolution conforms to the 2×4×3 pattern of lines & broken lines in the eight trigrams:
|
1st outer/inner half-revolution |
2nd outer/inner half-revolution |
|
|
|
1st gauge charge in revolution 1 1st gauge charge in revolution 2 1st gauge charge in revolution 3 |
8th gauge charge in revolution 1 8th gauge charge in revolution 2 8th gauge charge in revolution 3 |
| 2nd gauge charge in revolution 1 2nd gauge charge in revolution 2 2nd gauge charge in revolution 3 |
7th gauge charge in revolution 1 7th gauge charge in revolution 2 7th gauge charge in revolution 3 |
|
| 3rd gauge charge in revolution 1 3rd gauge charge in revolution 2 3rd gauge charge in revolution 3 |
6th gauge charge in revolution 1 6th gauge charge in revolution 2 6th gauge charge in revolution 3 |
|
| 4th gauge charge
in revolution 1 4th gauge charge in revolution 2 4th gauge charge in revolution 3 |
5th gauge charge in revolution 1 5th gauge charge in revolution 2 5th gauge charge in revolution 3 |
The nature of what property of the E8′ gauge charges (other than that of being either sources or sinks of gauge fields) corresponds to the yang/yin polarities of lines & broken lines has yet to be determined. However, we shall show on the next page that the eightfold distribution of charges in a closed curve with the topology of a circle arises from the mathematical fact that the 240 vertices of the Gosset polytope (see here) that represent the 240 roots of E8 (or E8′) have a Coxeter plane projection that is the compound of two 600-cells, each of which is a compound of 15 16-cells. As the 4-d counterpart of the octahedron, whose three pairs of vertices are equally spaced on either side of the X, Y & Z axes, the 16-cell has four pairs of vertices arranged at +1 and − 1 along each one of the four Cartesian axes, so that the 24 lines & broken lines in the set of eight trigrams symbolise the 24 vertices of a 24-cell, which is the compound of three 16-cells. This means that the yang/yin polarity of the analogous lines and unbroken lines refers to whether the Cartesian coordinate of the associated vertex is positive or negative with respect to the centre of each 16-cell, all three having 12 positive and 12 negative values that correspond to the 12 lines and 12 broken lines in the eight trigrams.
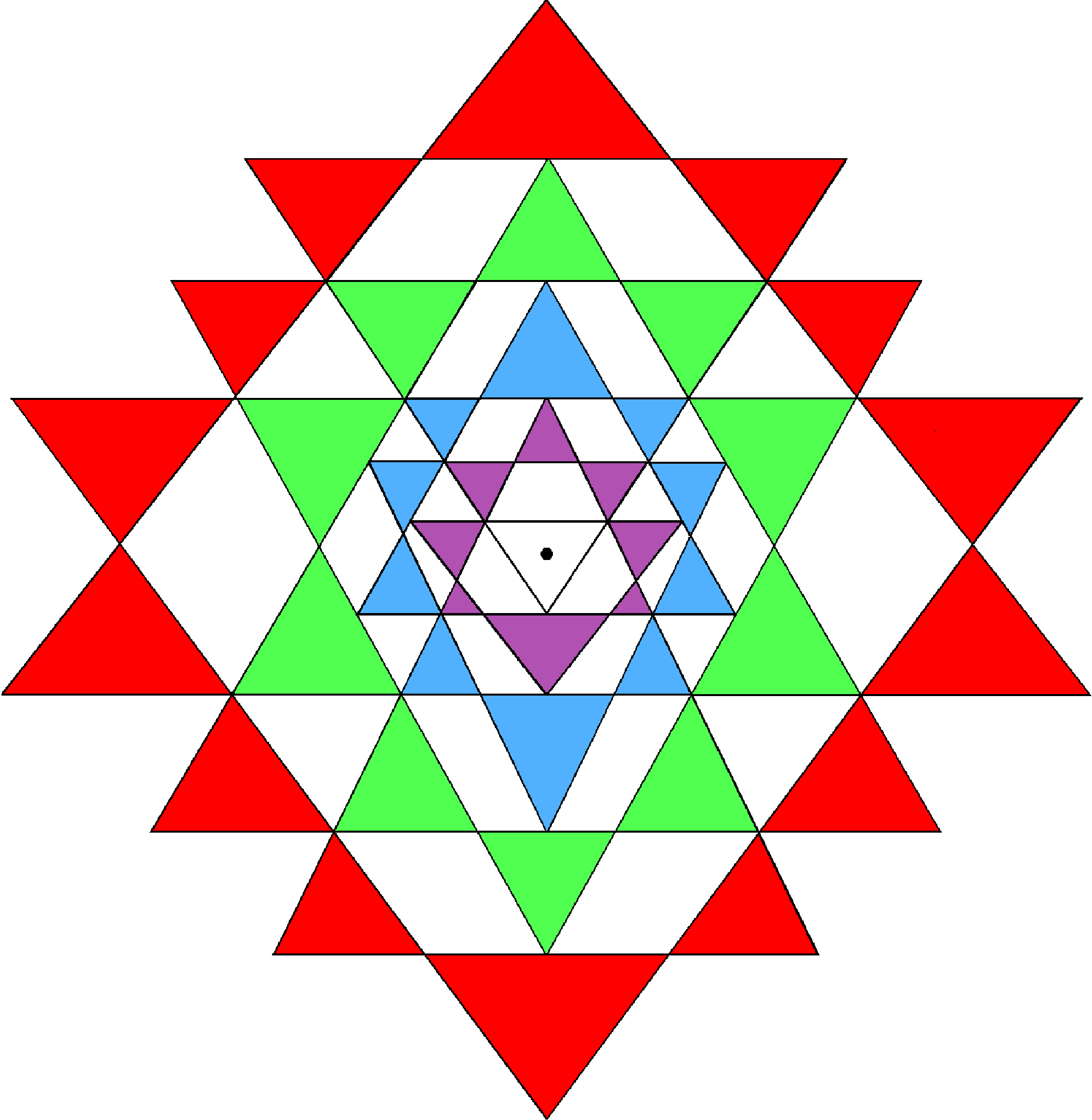
Not only does the Sri Yantra embody the superstring structural parameter 336 but its 2-d representation is also composed of 240 geometrical elements (69 points, 129 sides & 42 triangles), thereby embodying the number of roots of E8:
 |
 |
|
|
|
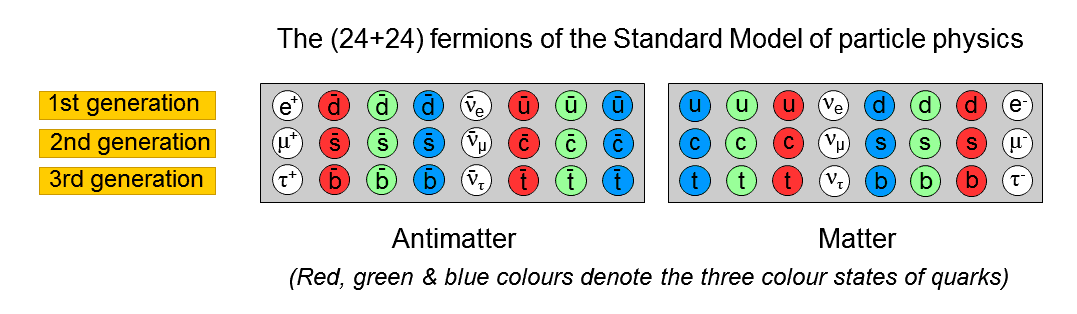
Below is a comparison of the eight trigrams and the 24 basic particles of the Standard Model and their antiparticles:
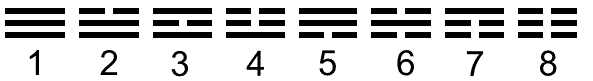 |
 |
|
The eight trigrams. |
The 24 fermions of the Standard Model and their antiparticles. |
Here is evidence of the 8×3 pattern found not only in the compound of three 16-cells that make up a 24-cell but also in the three generations of quarks and leptons discovered by particle physics. Notice that each generation divides into two sets of four fermions (three quark colour states & a lepton) because they are members of doublets of the weak isospin group SU(2) with electric charge Q & (Q−1), where Q = 2/3 or 0, just as the octet of trigrams divides into two quartets (1-4 & 5-8), whose corresponding members have lines and broken lines interchanged. The four authentic modes and the four plagal modes in the plainsong of the Roman Catholic Church are their musical counterpart (see here). The sacred-geometrical symbol of this 4:4 division in holistic systems is that of two interlaced squares, their corners forming an eight-pointed star:
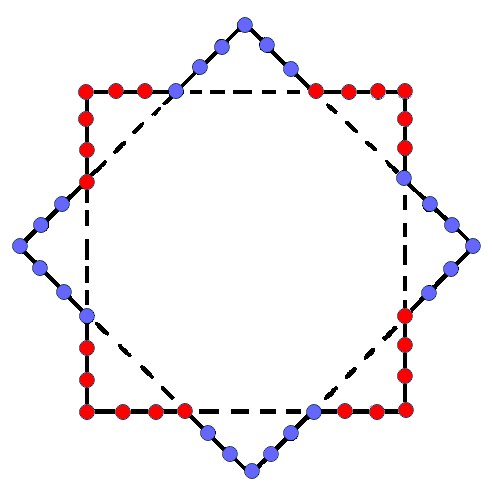 |
(24+24=48) yods line two squares with a relative orientation of 45°. Each square is lined by 24 yods (4 sets of 6, or 8 sets of 3). This reproduces the 8×3 pattern of the 8 trigrams and the 2×8×3 pattern of 8 hexagrams. |
The two squares are shaped by 48 yods, 24 per square. This 24:24 division is characteristic of holistic systems, as illustrated above for the 24 fermions of the Standard Model and their 24 antiparticles and as manifested in a whorl of the shadow matter particle, whose three outer revolutions carry (3×8=24) E8′ gauge charges and whose three inner revolutions, likewise, carry 24 E8′ gauge charges. A square whose sectors are 2nd-order tetractyses contains 248 hexagonal yods that symbolise the 248 roots of E8 (or, in this case, E8′):
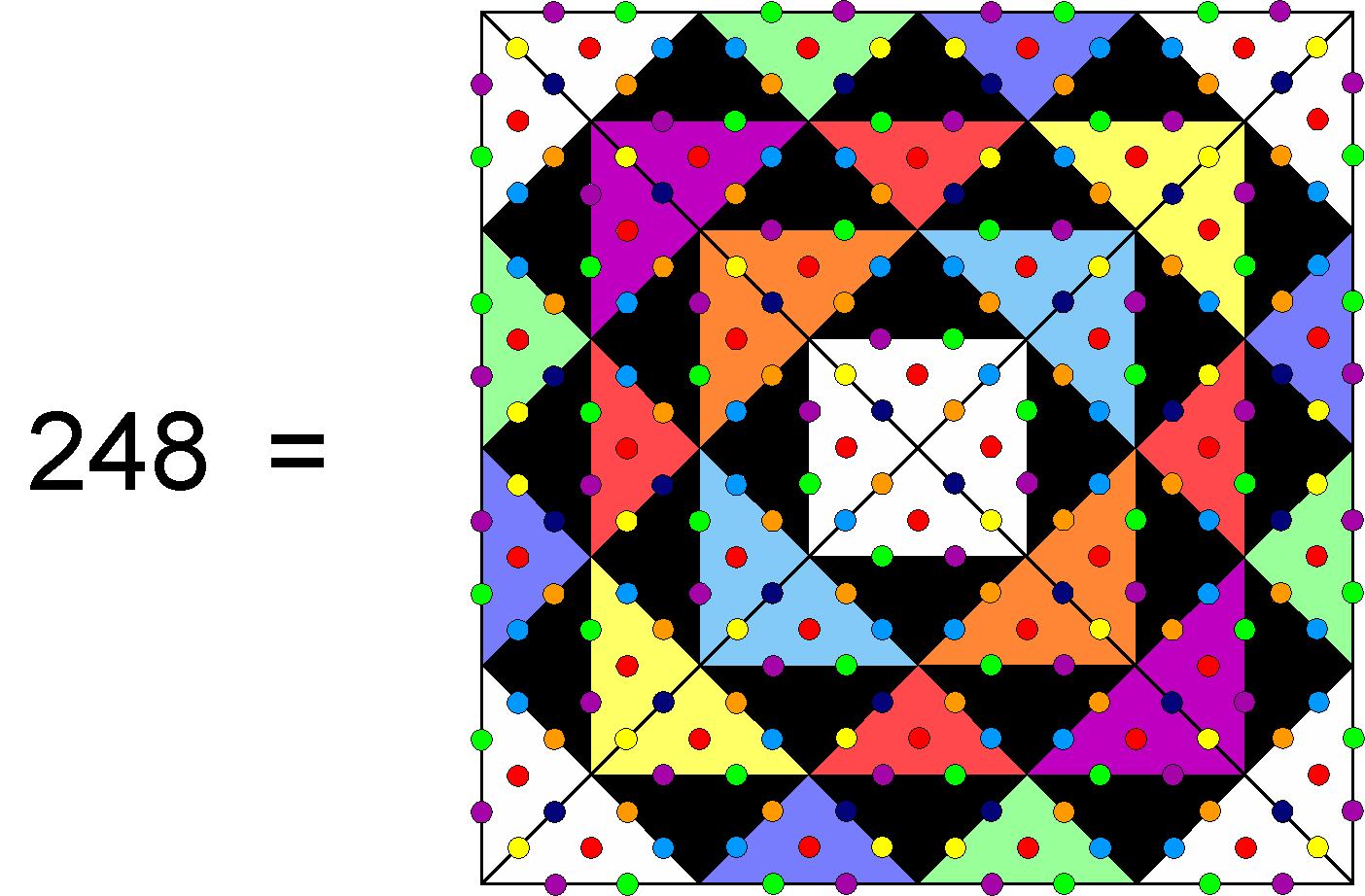 |
The square embodies the dimension 248 of E8 because, when constructed from 2nd-order tetractyses, it has 248 hexagonal yods that symbolise the 248 roots of E8. |
The square is the symbol of the Tetrad, which arithmetically determines the structural parameter 10080 of the shadow matter particle because 10080 = 30×336, where
30 = 12 + 22 + 32 + 42
(sum of the squares of the first four integers)
and
336 = 22 + 62 + 102 + 142
(sum of the squares of the first four even integers that are four units aparts).
| << Previous 1... 7 8 [9] 10 11 ...24 Next >> |