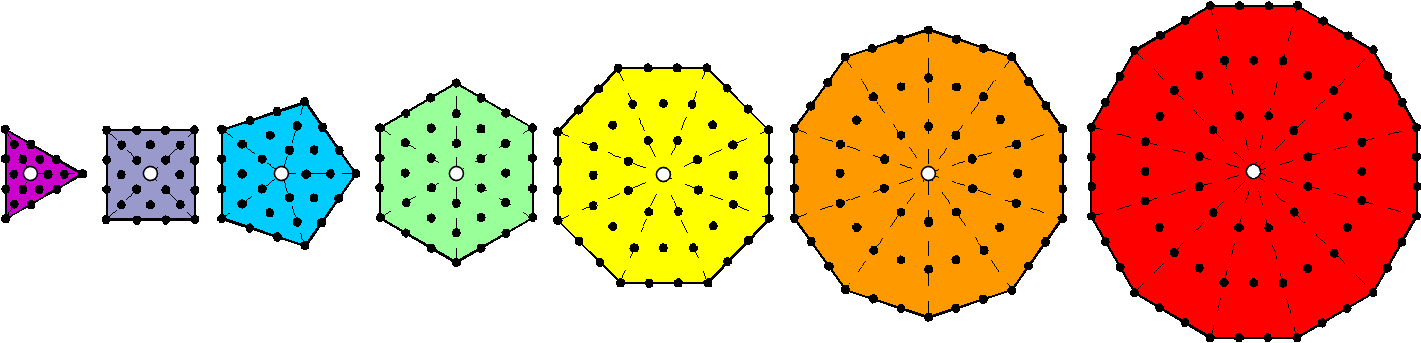
288 yods surround the centres of the 7 Type A polygons.
| << Previous 1... 4 5 [6] 7 8 ...24 Next >> |
#6The Tetrahedral Lambda basis of the UPA and shadow matter particle
We shall reveal here the connection between the Tetrahedral Lambda and the numbers of circularly polarised oscillations in the whorls of the UPA and the basic particle of shadow matter. This indicates that — whatever the mathematical form of their description turns out to be, their oscillations as superstrings conform to the arithmetic pattern that was outlined by Plato in his cosmology of the musical harmonies of the celestial spheres. In other words, there exists a remarkable analogy between the vibrations of superstrings and the vibrations of air that produce music — one that exceeds any superficial comparison with musical sound waves that one might find in popular science books about superstrings.
As was pointed out on page 1, the sum of the 20 number weights making up the general Tetrahedral Lambda with the integer N at the centre of its 1st face = 350N/6. It is useful to keep this expression as it is rather than simplify it to 175N/3 because the denominator 6 and the factors 7 & 50 of the number 350 have an interpretation vis-à-vis the inner Tree of Life, as we show shortly. It was also pointed out that, when N = 288, the sum of the 20 number weights = 50×7×288/6 = 50×7×48 = 50×336 = 16800. This is the total number of turns ("1st-order spirillae") in the 10 whorls of the UPA! Moreover, this factorisation reproduces its 3-dimensional structure, for its 10 whorls make 50 revolutions around its axis of spin, each complete revolution consisting of 336 turns. The number 288 is, of course, not only a number weight but also the tone ratio of the major 2nd of the ninth octave: 288 = 9/8×28. All the integer number weights above 1 in the Tetrahedral Lambda with N = 6 are tone ratios of overtones, and 288 is the 28th overtone, where
28 = 1 + 2 + 3 + 4 + 5 + 6 + 7
is the seventh triangular number. The arithmetic mean of the 20 number weights = 16800/20 = 840, which is the sum of the 28 odd integers after 1 because 292 − 1 = 840:
|
|
|
|
|
3 |
|
|
|
||||||
|
|
|
|
5 |
|
7 |
|
|
||||||
|
|
|
9 |
11 |
13 |
|
||||||||
| 840 = |
|
15 |
|
17 |
|
19 |
|
21 |
|||||
| 23 |
|
25 |
|
27 |
|
29 |
|
31 | |||||
| 33 |
|
35 |
|
37 |
|
39 |
|
41 | 43 | ||||
| 45 |
47 |
49 |
|
51 |
|
53 | 55 | 57 . |
This is the number of turns in each outer or inner half of a whorl because the UPA has 10 whorls with 20 halves. We found on page 1 that each of the 240 E8 gauge charges is spread over a section of a helical whorl of the UPA that contains 70 turns, whilst in the shadow matter particle they are spread over 42 turns. Therefore, the UPA needs 28 more turns for each charge than the shadow matter particle. These examples serve to illustrate the role of the number 28 in determining the structural parameters of the UPA. The number 6 at the centre of the Lambda Tetractys is the first perfect number because 6 = 1 + 2 + 3, where 1, 2 & 3 are its divisors. The number 1 is at the apex and the numbers 2 and 3 are the basic number weights generating the Lambda Tetractys. The second perfect number is 28 because 28 = 1 + 2 + 4 + 7 + 14, where 1, 2, 4, 7 & 14 are its divisors. 496 is the third perfect number. It is the gematria number value of Malkuth, the last Sephirah in the Tree of Life and signifying the material form of whatever is designed according to this blueprint. This number is the dimension of E8×E8′ and SO(32), the symmetry groups of the two types of heterotic superstrings. The note with tone ratio 6 is the fourth overtone, so that 288 is the 24th overtone after 6, where 24 = 4!. Given that 288 = 1!×2!×3!×4!, where 1, 2, 3 & 4 are the number of dots in the four rows of the tetractys, we see that this number has special Pythagorean significance, for it is the number of tetractys arrays of 10 objects that can be generated by independently permutating the objects in each of its four rows. Indeed, as 172 − 1 = 288, this number is the sum of the first 16 odd integers after 1 that form a 4×4 square array:
| 3 | 5 | 7 | 9 | |
| 288 = | 11 | 13 | 15 | 17 |
| 19 | 21 | 23 | 25 | |
| 27 | 29 | 31 | 33 |
Given that the tetractys represents the number 10 as the fourth triangular number and that the ancient Pythagoreans emphasised the central importance of the number 4, calling it "the greatest miracle," "a manifold divinity" and "the fountain of Nature," it is obvious that the number 288 has a unique, Pythagorean status. It also has Kabbalistic significance because it is the number of yods that surround the centres of the seven regular Type A polygons making up each half of the inner Tree of Life:
 |
|
|
Surrounding the centre of a Type A polygon with n corners are 6n yods. The seven polygons have 48 corners, where 48 is the number value of Kokab, the Mundane Chakra of Hod. There are (6×48=288) yods surround their centres. Compare this with the number of SLs in the n-tree: S(n) = 6n + 5. The number of SLs in every 48 Trees = S(n+48) − S(n) = 6×48 = 288. There are 288 SLs between any SL in the 1-tree (the lowest Tree in CTOL) and its counterpart in the 49th Tree, which is the Tree mapping the highest subplane of the cosmic physical plane. The factor of 6 in the number 288 expresses the six SLs per Tree and the factor of 48 expresses the number of Trees needed to be emanated before reaching the lowest one. If we shift the Lambda Tetractys from the position in the infinite lattice of number weights with 1 at its apex to the one with 48 at its apex, its central integer is 288 because — wherever its location in the lattice — its central number is always six times whatever is the number at its vertex. The sum of the 20 number weights in the general Tetrahedral Lambda is 350N/6, that is, 350 times the number N/6 at its apex, so that, when N = 288, the sum is 350×48 = 16800, the total number of turns in the 10 helical whorls of the UPA:
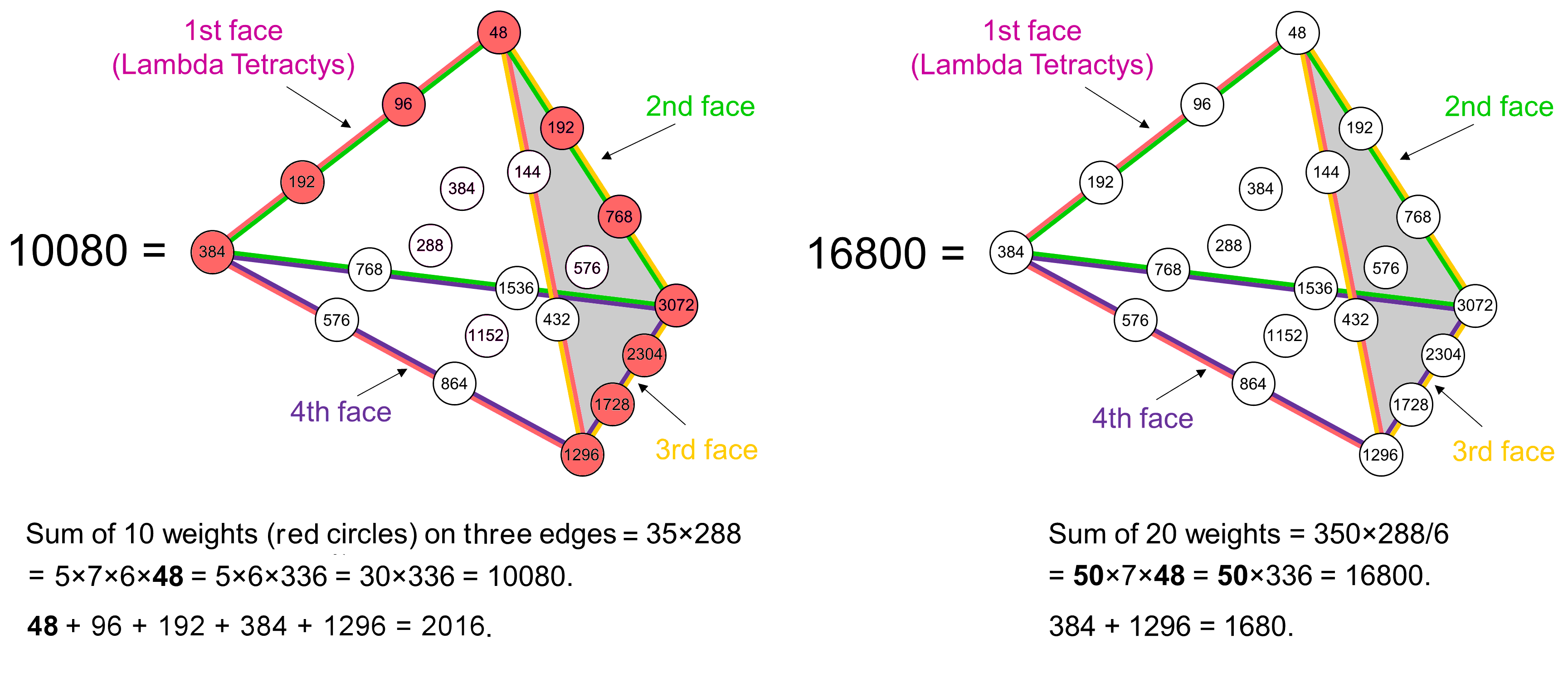
Notice that the sum of the number weights at the two lower corners of the 1st face is 1680. How plausible is it that both the number of turns in one whorl of the UPA and the number in all 10 whorls could be expressed so transparently just by chance? Notice also that the sum of the first three number weights 48, 96 & 192 that correspond to the integers 1, 2 & 4 in the Lambda Tetractys with 6 at its centre is 336, which is the number of turns per revolution of a whorl in either the UPA or the shadow matter particle.
Is there some integer value of N for which the general Tetrahedral Lambda can represent either the structural parameters 10080 or 2016 of the shadow matter particle? The former is 3/5 of 16800, so the corresponding number weight N would have to be (3/5)×288. But 288 is not divisible exactly by 5, so no integer exists that allows this, quite apart from it having to be a number weight of the Pythagorean musical scale. Similarly, the latter is 6/5 of 1680, i.e., 3/25 of 16800, so N would have to be (3/25)×288, which is not an integer. The two parameters must be represented by a subset of the 20 integers of the Tetrahedral Lambda with 48 at its apex. As 10080 = 35×288, the subset can exist in principle because 35 is exactly divisible by 5, the number of whorls in the shadow matter particle. To find it, it is better to consider the general Tetrahedral Lambda with N at the centre of its 1st face, shown on page 2. Then we need to look for weights that add up to 35N. But more is needed. They also ought to constitute a definite, well-defined class of number weights, otherwise they will merely look like a cherry-picked collection of numbers, which does not amount to convincing evidence for the Tetrahedral Lambda embodying these structural parameters of the shadow matter particle. They must also contain a subset of weights that add up to 2016, just as all 20 weights contain two that add up to 1680. This is possible if the set of weights adding to 35N contains weights adding to 7N, which is 2016 when N = 288. The sum of the 10 weights (shown by red circles in the diagram above) on three complete edges of the general Tetrahedral Lambda = N/6 + N/3 + 2N/3 + 4N/3 + 9N/2 + 2N/3 + 8N/3 + 32N/3 + 8N + 6N = 35N. This is 10080 when N = 288. The weights N/6, N/3, 2N/3, 4N/3 & 9N/2 add up to 7N. Therefore, there is a set of weights whose sum is 10080 and which contains a subset adding to 2016. The latter is the four number weights 48, 96, 192 & 384 on the left-hand side of Plato's Lambda expressing the four powers of 2 and the number weight 1296 at the end of its right-hand side:
(48+96+192) + (384+1296) = 336 + 1680 = 2016.
This property expresses the difference between the six revolutions of a whorl of the shadow matter particle and the five revolutions of a whorl of the UPA: it amounts to one more revolution with 336 turns, i.e., 1/5th more of the UPA's whorl. Revealed here is the 6/5 proportion displayed by the branches and trunk of the Tree of Life, the former comprising 11 triangles with 12 sides and the latter comprising five triangles with 10 sides, where 12/10 = 6/5.
The factorisation:
35×288 = 5×7×6×48 = 5×6×336 = 10080
is interpretable for the shadow matter particle as the five helical whorls, each with six revolutions containing 336 turns per revolution. The factorisation of the sum of all 20 number weights:
350×288/6 = 10×5×7×48 = 10×5×336 = 16800
is interpretable for the UPA as the 10 helical whorls, each with five revolutions containing 336 turns per revolution. It is remarkable that, not only does the Tetrahedral Lambda and a subset of its weights generate the numbers of turns in the two particles, they do so in a way that arithmetically reproduces in each case the number of whorls and the number of revolutions in each whorl. It is implausible that all these connections with features of the two types of superstring could arise by chance — particularly when the integer 48 at the apex of the Tetrahedral Lambda is the number of corners of the seven polygons in each half of the inner Tree of Life and the integer 288 at the centre of its first face is the number of yods surrounding their centres.
As 10080 = 30×336 and 16800 = 50×336, the two particles have (30+50=80)×336 turns. The number 80 is the gematria number value of Yesod, the penultimate Sephirah of Construction. It is remarkable that the number value 496 of Malkuth is the number of gauge fields of the two symmetry groups SO(32) and E8×E8′ that are free of quantum anomalies and that the number 80 of Yesod determines the number of circularly polarised waves in the 15 whorls of the E8-singlet and E8′-singlet states of the E8×E8′ heterotic superstring. The division: 80 = 30 + 50 has its counterpart in the outer Tree of Life because, when its 19 triangles are tetractyses, the 1-tree has 80 yods that comprise 30 yods in its so-called "Upper Face" (the kite shape with corners at Kether, Chokmah, Binah & Tiphareth) and 50 yods below it:
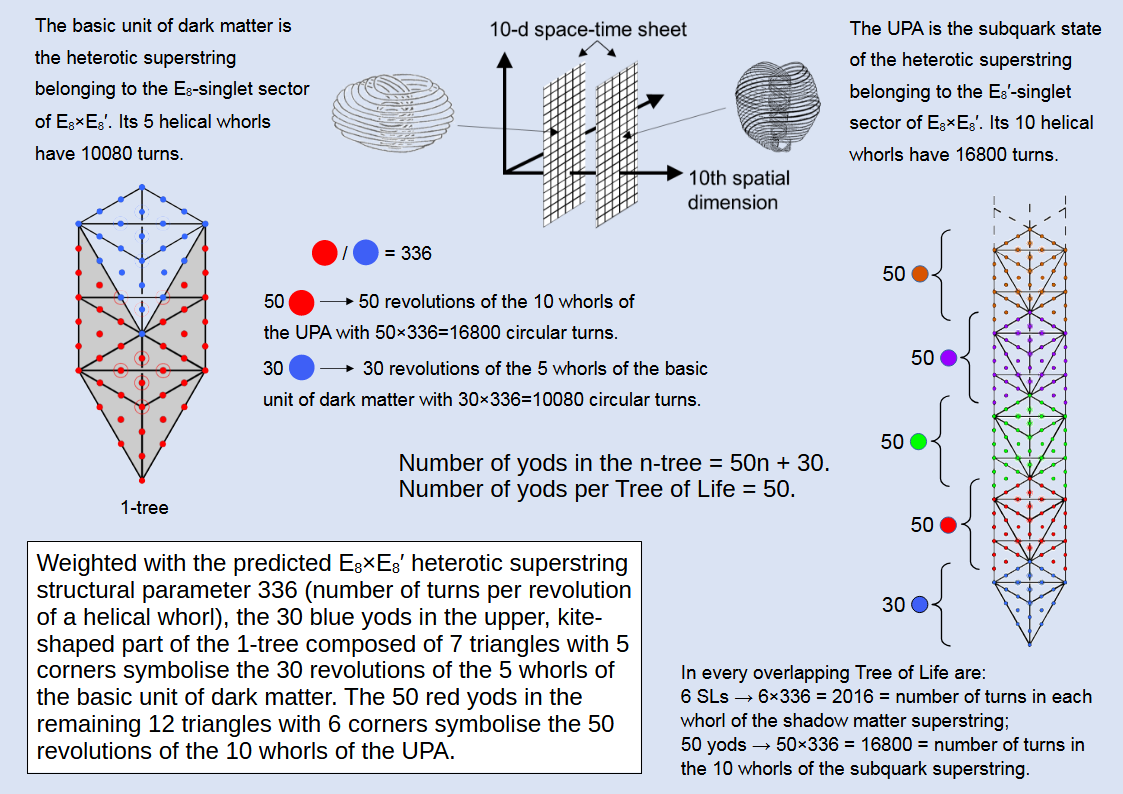
Each yod in the Upper Face denotes one revolution of a whorl of the shadow matter particle. Each yod below it denotes one revolution of a whorl of the UPA. The division is mathematically expressed in the formula for the number of yods (Y(n)) in the n-tree constructed from tetractyses:
Y(n) = 50n + 30,
so that Y(1) = 80 = 50 + 30, although the number 30 here refers to the 30 yods in the lower, kite shape, whose corners are located at Malkuth, Hod, Netzach & Tiphareth (with the lattermost included in the count), whilst the number 50 refers to the 50 yods above this shape — see diagram above. The number of yods in successive Trees of Life = Y(n+1) − Y(n) = 50, the gematria number value of ELOHIM, the Godname of Binah. Weighted with 336, every successive Tree embodies the number of turns in the 10 helical whorls of the UPA. The number of SLs (S(n)) in the n-tree is
S(n) = 6n + 5.
Every successive Tree adds S(n+1) − S(n) = 6 SLs. Weighted with 336, the 50 yods per Tree includes six SLs whose total weight = 6×336 = 2016, which is the number of turns in each whorl of the shadow matter particle. The outer form of successive Trees embodies the structural parameters 16800 and 2016 of, respectively, the subquark and shadow matter particle states of the E8×E8′ heterotic superstring.
Every seven Trees of Life, each expressing a Sephirah of Construction, contain 350 yods:
Y(n+7) − Y(n) = 7×50 = 350.
As there are seven Sephiroth of Construction, the emanation of seven successive Trees constitutes a complete cycle — just as the seven notes above the tonic of an eight-note musical scale do. This illustrates the holistic character of the number 350 as the sum of the 20 number weights in the Tetrahedral Lambda with the Lambda Tetractys as its 1st face. Its counterpart in the inner form of the Tree of Life is the set of 350 hexagonal yods that line the sides of the 94 tetractyses in its (7+7) enfolded Type A polygons:
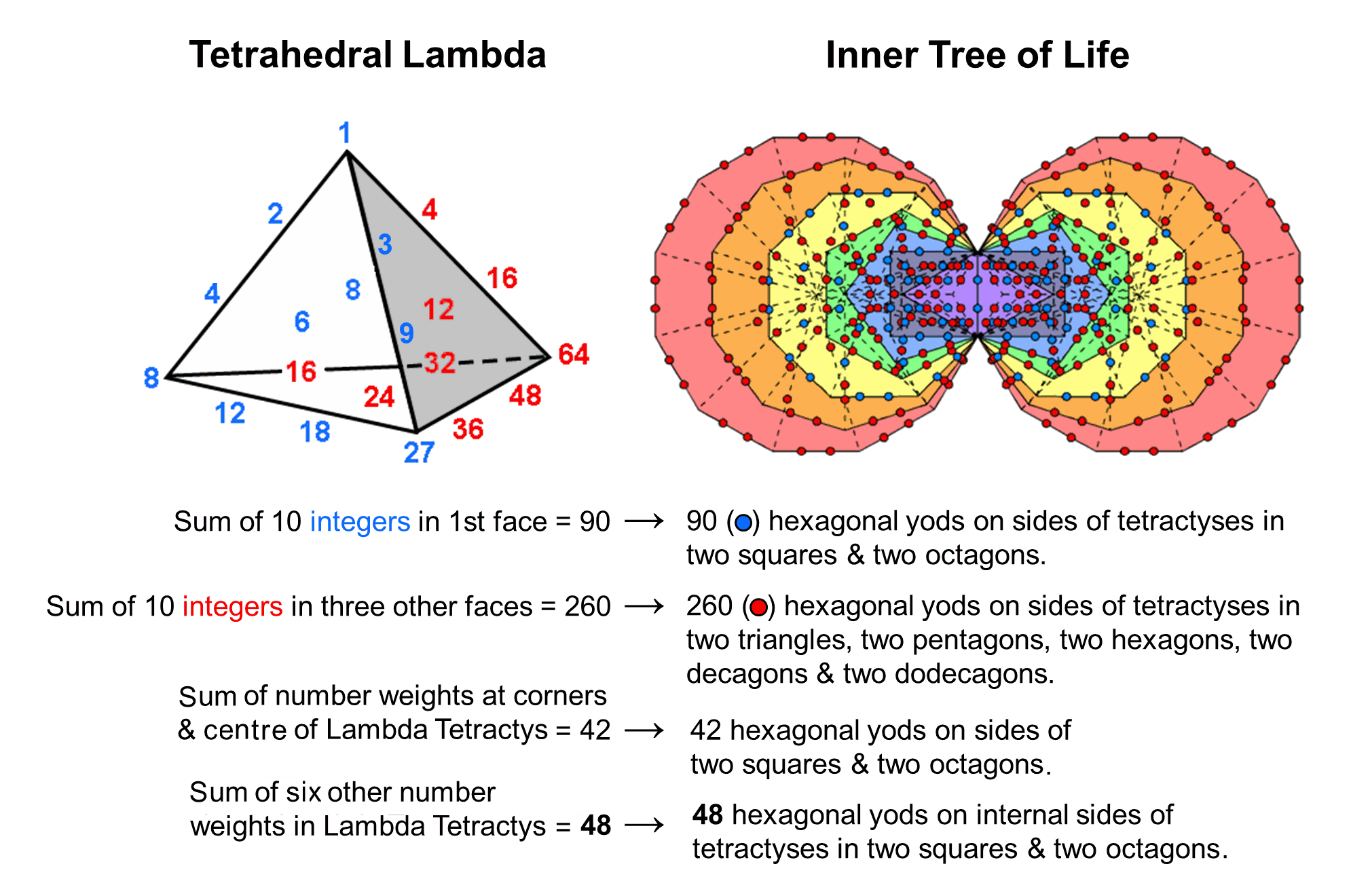
Shown above are some of the analogous features of these isomorphic representations of holistic systems.
| << Previous 1... 4 5 [6] 7 8 ...24 Next >> |