
| << Previous 1... 3 4 [5] 6 7 ...24 Next >> |
5. A 2nd-order tetractys representation of the compound of two 600-cells
|
|
 |
A 2nd-order tetractys contains 85 yods, where
85 = 40 + 41 + 42 + 43.
Including the yods at the centres of the six triangular gaps between the 1st-order tetractyses in the 2nd-order tetractys generates a triangular array of 91 yods, where
91 = 12 + 22 + 32 + 42 + 52 + 62.
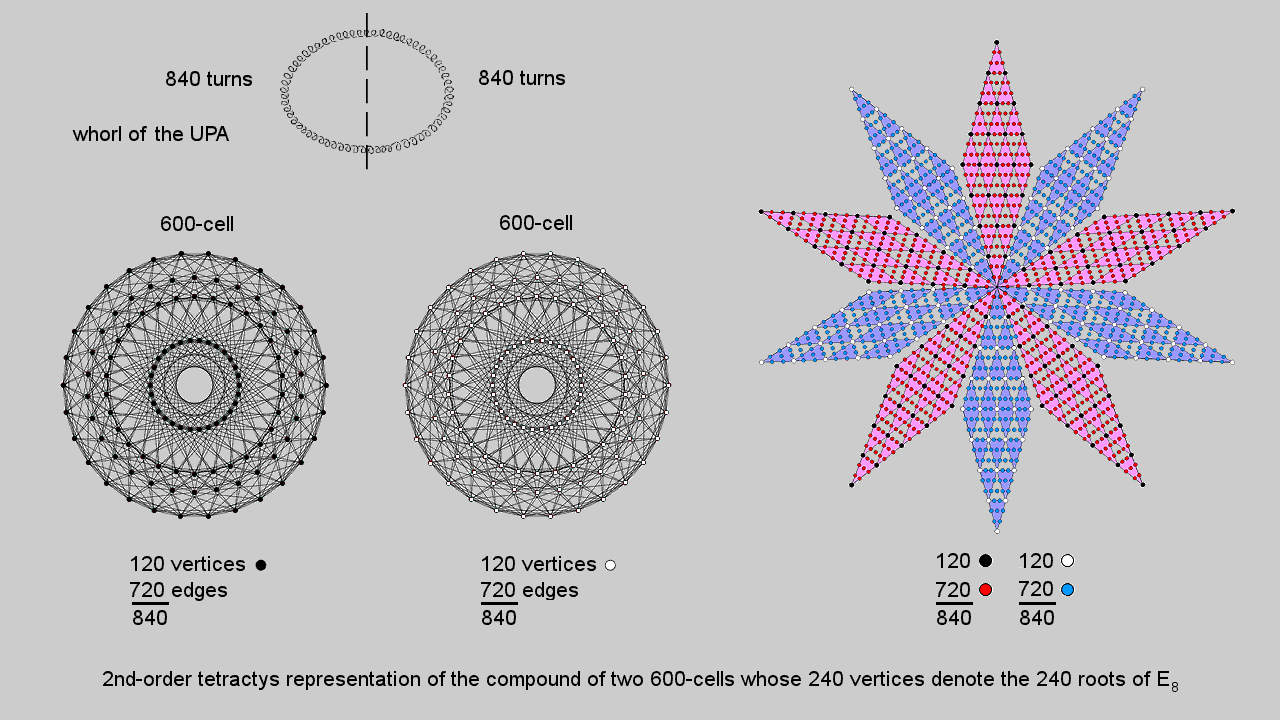
13 yods line each side of the array, so that a parallelogram made up of two triangular arrays of 91 yods placed back to back contains (91+91−13=169) yods. Surrounding the centre of a 10-pointed star whose points are these arrays are 1680 yods. Each 5-pointed star has 840 yods. Each point of the star contains 120 corners of 1st-order tetractyses and 720 hexagonal yods. The red 5-pointed star contains 120 black corners of 1st-order tetractyses and 720 red hexagonal yods. The blue 5-pointed star contains 120 white corners of 1st-order tetractyses and 720 blue hexagonal yods. The 1680 yods in the 10-pointed star comprise 240 corners of tetractyses and 1440 hexagonal yods. Compare this with the fact that a 600-cell is a polychoron with 120 vertices and 720 edges. The 10-pointed star is a representation of the compound of two 600-cells with 240 vertices and 1440 edges, each 5-pointed star representing a 600-cell. The 240 corners of 1st-order tetractyses denote the 240 vertices of the compound and the 1440 hexagonal yods denote the 1440 edges.
Each point of the star contains 24 corners of 1st-order tetractyses. They correspond to the 24 vertices of a 24-cell, each 5-pointed star representing the compound of five disjoint 24-cells that make up a 600-cell. We saw in the last section that the 24 vertices of a 24-cell consist of the eight vertices of a 16-cell and the 16 vertices of an 8-cell. In the point of the 10-pointed star, they correspond to the eight corners of tetractyses outside the corner shared between star points that line two adjacent sides of the parallelogram and to the remaining 16 corners.
This 10-pointed star representation of the 240 vertices of a compound of two 600-cells as the 4-dimensional projection of the 240 roots of E8 mapped by the 8-dimensional 421 polytope is a particularly clear demonstration of the 10-foldness of this number displayed by sacred geometries, as explained in #2. It should not, therefore, come as a surprise that the 1680 turns of each helical whorl of the UPA/heterotic superstring are generated in 10 half-revolutions (180°). The outer five half-revolutions of a whorl with 840 turns are represented by the 840 yods (120 corners, 720 hexagonal yods) in one 5-pointed star and its inner five half-revolutions with 840 turns are represented by the 840 yods in the other 5-pointed star. However, if we want to retain the correspondence between the 240 corners of tetractyses and the 240 vertices of the two 600-cells determining the 240 roots of E8, this correspondence cannot be interpreted as referring to a single whorl. Rather, each point in the 10-pointed star must correspond to either a whorl or (as we concluded in earlier sections) a half-revolution of all 10 whorls of the UPA, which is represented by the whole star because, being the E8′ singlet state of an E8×E8′ heterotic superstring, the UPA "carries" the 240 gauge charges of E8 corresponding to its roots.
The counterpart of this in the inner form of 10 Trees of Life (see the right-hand picture shown above) is the 1680 corners of the 2820 triangles in the (70+70) Type B polygons that are unshared with the Trees.* They comprise (120+120=240) red corners of the sectors of the 20 dodecagons and 720 remaining corners in each set of 70 enfolded polygons that are unshared with the triangles of the outer Trees of Life. This demonstrates in an unequivocal way the Tree of Life basis of the 120 vertices & 720 edges of each 600-cell.
* Proof: either set of seven enfolded polygons has 47 sectors with 41 corners. When the polygons are Type B, these sectors are composed of (3×47=141) triangles with (47+41=88) corners. Three of these lie on either side pillar of the outer Tree of Life and are corners of triangles belonging to the latter. It leaves (88−3=85) corners that are intrinsic to either set of polygons. One corner (an endpoint of the root edge shared by all the polygons) can be associated with one set of polygons and the other endpoint can be associated with the other set. Hence, 84 corners are intrinsic to each set of Type B polygons. Both sets of polygons have 94 sectors composed of 282 triangles with (84+84=168) corners unshared with the outer Tree of Life. The (70+70=140) Type B polygons enfolded in 10 Trees of Life are composed of 2820 triangles with 1680 intrinsic corners. This is how the inner form of 10 Trees of Life mapping the 10 half-revolutions of a whorl, each of 168 turns, embodies the superstring structural parameter 1680 discovered by Charles Leadbeater over a century ago when he examined the UPA with micro-psi (see here).
| << Previous 1... 3 4 [5] 6 7 ...24 Next >> |