

The two 600-cells
The 3-dimensional projection of the rotating 600-cell. Two different-sized 600-cells sharing the same centre have the same distribution of vertices as the Petrie projection of the 421 polytope. (Compare their Petrie polygons in Figure 2 on #2). Its 240 vertices can be divided into two sets of 120 vertices, whose projections are the vertices of the two 600-cells. They are represented in sacred geometries by the (120+120=240) geometrical elements or structural components in the two halves of the geometry, each half being composed of 5 sets of 24 that correspond to the 5 24-cells in each 600-cell. In the UPA/superstring, these 2-fold and 5-fold patterns manifest as the inner and outer halves of its 10 whorls, each half consisting of their 5 half-revolutions around its spin axis.
(Credit: "600-cell" by Jason Hise, uploaded to Wikipedia.org.).


Zome model of the 600-cell as a compound of 5 24-cells.
(Credit: http://homepages.wmich.edu/~drichter/five24cells.htm).
The 7 enfolded polygons
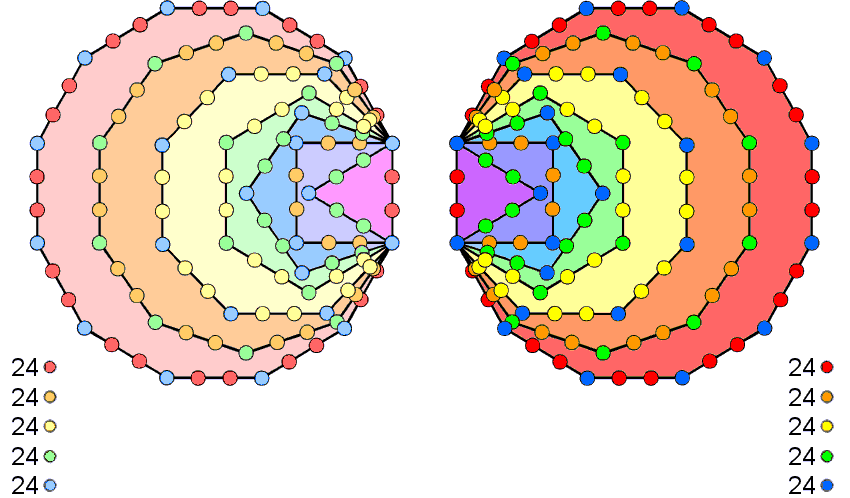
120 yods line the 42 sides of the 7 enfolded polygons constituting either half of the inner Tree of Life when their sectors are tetractyses. Considered as separate sets of 7 enfolded polygons, (120+120=240) yods line their 84 sides. They comprise 72 corners and 168 hexagonal yods. This 72:168 division is characteristic of sacred geometries (see The holistic pattern). The numbers of corners & hexagonal yods on the sides of a set of 7 enfolded polygons, including their shared root edge, are shown below:
| root edge | triangle | square | pentagon | hexagon | octagon | decagon | dodecagon | |
| Corners | 2 | 1 | 2 | 3 | 4 | 6 | 8 | 10 |
| Hexagonal yods | 2 | 4 | 6 | 8 | 10 | 14 | 18 | 22 |
For the dodecagon, its 22 hexagonal yods can combine only with either the 2 corners or the 2 hexagonal yods in the root edge in order to form a set of 24 yods; the latter is the more natural option. The 18 hexagonal yods in the decagon can combine only with the 6 hexagonal yods in the square to form a set of 24. Similarly, the 14 hexagonal yods in the octagon can combine only with the 10 hexagonal yods in the hexagon to form a set of 24. The remaining 12 hexagonal yods in the triangle and pentagon must combine with 12 corners so as to leave 24 corners as two subsets of 12. This can happen in several ways. The issue at stake here is not which is the correct one but the fact that such combinations are possible. This means that the 120 boundary yods can be divided into 5 sets of 24 in a non-trivial way, i.e., one in which a set is composed only of yods from complete polygons, not from bits and pieces of them. The diagram depicts the two separate sets of 7 enfolded polygons. 120 yods as 5 sets of 24 coloured in dark hues of red, orange, yellow, green & blue line the sides of the right-hand set of polygons; 120 yods as 5 sets of 24 coloured light hues of red, orange, yellow, green & blue line the sides of the left-hand set of polygons.
The separate polygons of the inner Tree of Life
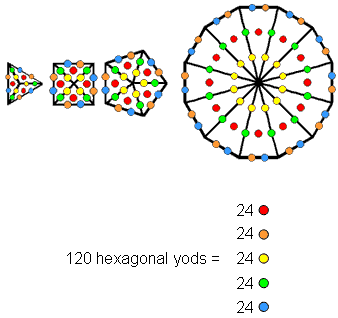
An n-gon with its n sectors turned into tetractyses has 5n hexagonal yods because there are 5 hexagonal yods per sector. The triangle (n=3), square (n=4), pentagon (n=5) & dodecagon (n=12) have 120 hexagonal yods in 24 tetractyses, 5 hexagonal yods per tetractys. The 5 classes of hexagonal yods are coloured red, orange, yellow, green & blue. The remaining three polygons in the inner Tree of Life are the hexagon (n=6), octagon (n=8) & decagon (n=10). They have 120 hexagonal yods distributed in 24 tetractyses as 5 hexagonal yods per tetractys. The 7 polygons divide into two sets of polygons, each with 24 tetractyses containing 120 hexagonal yods, 5 per tetractys. In other words, the 7 separate polygons that make up the inner form of the Tree of Life contain 240 hexagonal yods that form two sets of 120 hexagonal yods, each set consisting of 5 types of a subset of 24 yods.
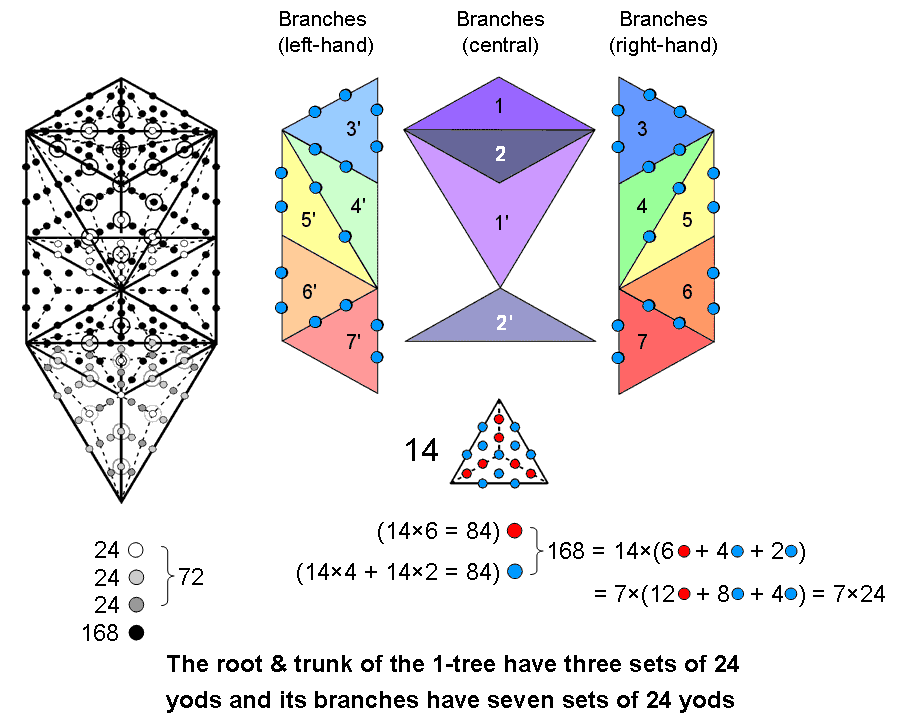
The 1-tree with Type A triangles
The 1-tree contains 240 yods other than Sephirothic corners of triangles when these 19 triangles are Type A. Its root and trunk consist of 3 sets of 24 yods (white, light grey & dark grey). Its branches comprise 7 sets of 24 black yods. The 36 yods aligned with the central Pillar of Equilibrium consist of 8 white yods, 4 light grey yods, 4 dark grey yods & 20 black yods. As these are all even integers, it is possible to associate half of the yods of each colour located on the Pillar of Equilibrium with the left side of the 1-tree and half with its right side. The 1-tree is its own mirror image, so that the numbers of yods in the 1-tree are:
|
Left |
Central Pillar |
Right |
|
| White |
8 |
4+4=8 |
8 |
| Light grey |
10 |
2+2=4 |
10 |
| Dark grey |
10 |
2+2=4 |
10 |
| Black |
74 |
10+10=20 |
74 |
| Total |
102 |
18+18=36 |
102 |
(102+4+2+2+10=120) yods can be associated with each half, including 18 yods that are aligned with the Pillar of Equilibrium. The table on #2 summarising the 10-fold pattern of sacred geometries showed that the 240 non-Sephirothic yods in the 1-tree form 10 sets of 24 yods (3 sets in its root & trunk and 7 sets in its branches). Five of these sets can be associated with each mirror-half of the 1-tree when the 36 yods on the axis of symmetry (which are their own mirror-images) are divided into two sets of 18 that are formally associated with their respective halves. How they are separated into these two sets and which set is associated with which half of the 1-tree are questions that need not detain us here, as it is sufficient to show that the geometry of the 1-tree permits its yod population to be divided into two sets of 120 yods, each forming 5 sets of 24 yods.
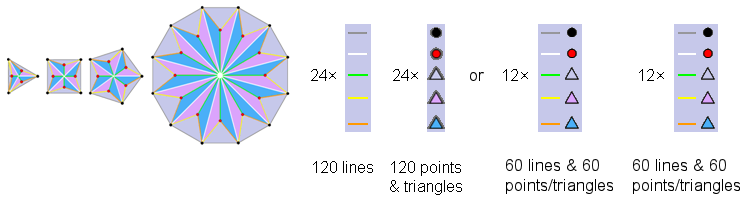
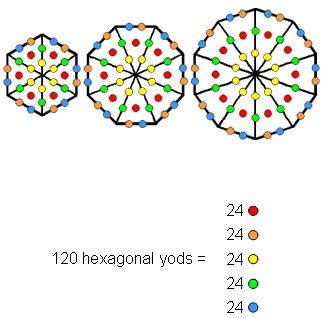
The Type A triangle, square, pentagon & dodecagon
Surrounding the centre of a Type B n-gon are n sectors, with 5 sides and 2 corners of 3 triangles (i.e., 5 corners or triangles) per sector. 10n geometrical elements surround its centre. Surrounding the centres of the Type B triangle (n=3), square (n=4) pentagon (n=5) are 10(3+4+5) = 120 geometrical elements. They comprise 5 types of 12 lines and 5 types of 12 points or triangles, i.e., 5 types of pairs of elements, each pair consisting of a line and either a point or triangle. Surrounding the centre of the Type B dodecagon are 120 geometrical elements with a similar geometrical composition because it has the same number of sectors as the first three polygons. These four Type B polygons comprise 120 lines as 5 types of (12+12=24) lines and 120 points & triangles as 5 types of 24 points or triangles. Only the former 120:120 division is consistent with the 36:84 division for the 120 yods lining the sides of the 7 enfolded polygons in the inner Tree of Life. This is because the sectors of the first 3 polygons have 36 corners & sides surrounding their centres, whereas a 36:84 division in lines picks out the 36 internal lines needed to transform the first three Type A polygons or the Type A dodecagon into Type B polygons and this goes against the fundamental character of the number 36 as the number of corners of the 7 enfolded polygons. A similar argument applies to the 36 triangles in the first 3 polygons. The 120:120 division of the 240 geometrical elements is generated by the distinction between the first 3 polygons and the dodecagon.
.png)
.png)
The pair of Type B dodecagons
Surrounding the centre of the Type B dodecagon are 120 geometrical elements that consist of 5 types of lines (repeated 12 times), two points (×12) & 3 triangles (×12), i.e., 5 geometrical elements (×12). Therefore, 5 sets of 12 pairs of geometrical elements surround the centre. Each pair comprises a side of a triangle and either a corner or triangle. The (7+7) polygons of the inner Tree of Life contain a pair of dodecagons. Surrounding the centres of the latter are (120+120=240) geometrical elements. Each set of 120 elements consists of 5 sets of 24 elements. The number 5 arises naturally as the number of either lines or points & triangles per sector of a Type B polygon. The number 24 arises as the product of the number 12 (a dodecagon has 12 sectors) and the number 2 (the 10 types of geometrical elements composing a Type B polygon consist of two distinct sets of 5 elements).
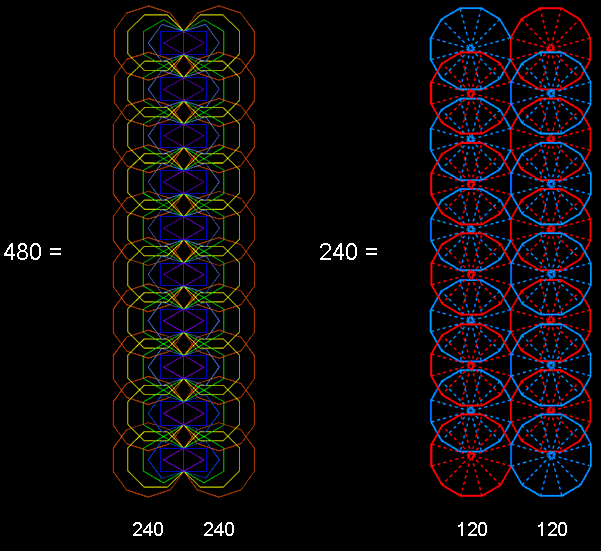
The inner form of 10 overlapping Trees of Life
The first (6+6) enfolded polygons of the inner Tree of Life have 50 corners. They are a holistic subset of the (7+7) polygons. The corners at the top of the two hexagons coincide with the lowest corners of the hexagons enfolded in the next higher Tree of Life. The number of corners of the 12n polygons of the first 6 types enfolded in the n-tree = 48n +2, where "2" refers to the two corners of the hexagons enfolded in the nth tree that are shared with the hexagons enfolded in the (n+1)th Tree. The 120 polygons of the first 6 types enfolded in the 10-tree have 480 corners that are intrinsic to them in the sense that they are not shared with any polygons enfolded in the 11th Tree. 240 corners are associated with each set of 60 polygons enfolded in the 10-tree. They denote the (240+240=480) roots of E8×E8, the symmetry of the unified force acting between one of the two types of heterotic superstring. Kabbalistically speaking, each overlapping Tree in the 10-tree represents a Sephirah. The upper Face of the Tree of Life spans the first six Sephiroth, counting from Kether, and its lower Face spans the last 5 Sephiroth. The interface of the two Faces is Tiphareth at the centre of the Tree. The 5:5 division of Sephiroth created by the upper & lower Faces creates a 120:120 division in the 240 corners associated with each set of 60 polygons. As 24 corners are associated with, and intrinsic to, each set of 6 enfolded polygons, the 120 corners associated with the 30 polygons of the first 6 types enfolded in 5 Trees of Life consist of 5 sets of 24. The 240 corners of the 60 polygons enfolded in 10 Trees therefore comprise two similar groups of 5 sets of 24 corners.
The dodecagon is the last regular polygon of the inner Tree of Life. The Type A dodecagon has 12 sectors with 13 corners. The two joined dodecagons have 24 sectors with 24 corners. The 5 pairs of dodecagons enfolded in the uppermost 5 Trees of the 10-tree have 120 corners, as do the 5 pairs of dodecagons enfolded in the lowest 5 Trees. The (5+5) pairs of dodecagons enfolded in the 10-tree reproduce in the 240 corners of their 240 sectors the same 5×24 pattern as the first 6 types of polygons enfolded in the uppermost or lowermost 5 Trees exhibit in their corners. It re-occurs because the first 6 polygons correspond to the 6 Sephiroth of Construction above Malkuth, to which the dodecagon corresponds. The archetypal pattern of the 240 roots of E8 represented by the 240 vertices of the two 600-cells takes form in the material universe.
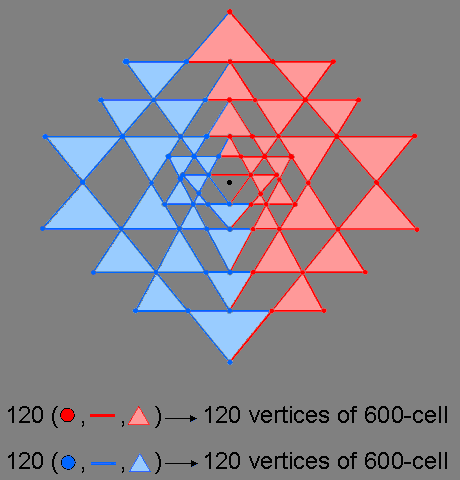
The 2-dimensional Sri Yantra as two sets of 120 geometrical elements
240 points, lines & triangles surround the centre of the 2-dimensional Sri Yantra. 13 points, lines & triangles above this centre span the vertical axis of symmetry that passes through it. 13 points, lines & triangles below the centre span the axis. 107 geometrical elements lie on either side of the axis. One set is the mirror image of the other. The upper set of 13 geometrical elements can be associated with either set of 107 elements (the right-hand side is chosen in the diagram). The 240 geometrical elements comprise 120 elements and their mirror images reflected across the vertical axis (this includes the 26 elements lying on the axis that are their own mirror images). They do not have exactly the same geometrical composition because the top red side of the central "triangle"* is associated with one set of red geometrical elements and its lowest blue corner is associated with the other set of blue geometrical elements, the two sets having the same composition. 236 geometrical elements belong, exclusively, to the 42 true triangles surrounding the central one.
*This is not really a triangle in the sense of enclosing its own 2-dimensional space because the "bindu" (the black dot in the diagram) is embedded in its plane as a separate, mathematical point.
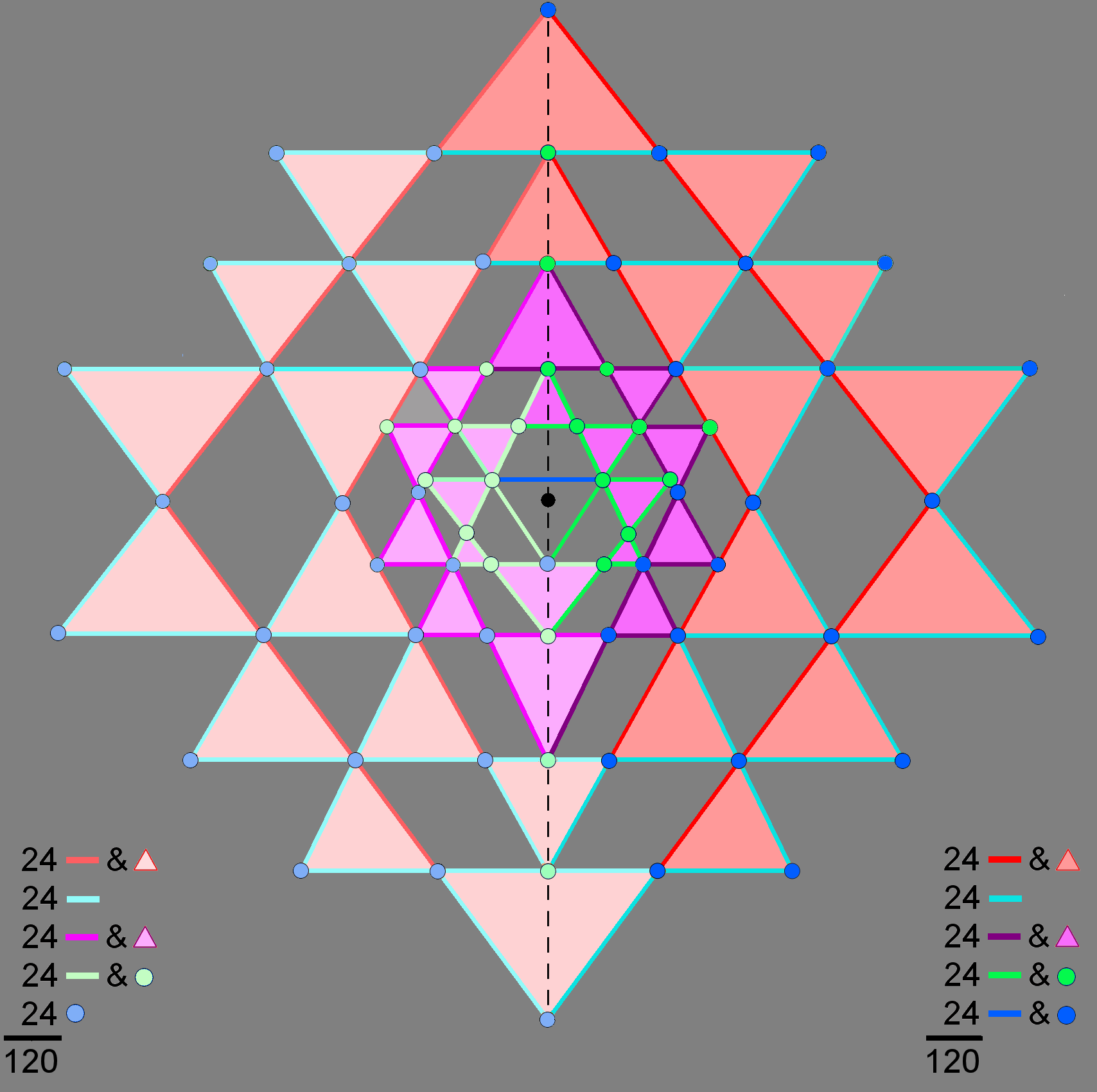
The 2-dimensional Sri Yantra as (5+5) sets of 24 geometrical elements
The 120 dark coloured corners, sides & triangles dark belonging to one side of the 2-d Sri Yantra are counterbalanced by their 120 light coloured mirror images, reflected across the central vertical mirror denoted by the dashed line that passes through the central, black dot (bindu) of the yantra. They express the cosmic duality of Shiva & Shakti or Yang & Yin, the male & female principles. The mirror images of the 13 dark coloured points, lines & triangles above the bindu that straddle the mirror/dashed line are defined to be the 13 light coloured points, lines & triangles lying below it that, too, straddle this line. The "mirror" counterpart of the dark blue line in the central triangle is the light blue dot that is its lowest corner below the bindu. Together with the light and dark green sides of the central triangle, these are the only geometrical elements that are not shared with the 42 triangles. The 118 geometrical elements that are intrinsic to each set of 21 triangles have their counterpart in the inner Tree of Life, the boundaries of whose (7+7) enfolded polygons are lined by 236 yods when their (47+47) sectors are tetractyses. Associated with each set of 7 enfolded polygons are 118 boundary yods.
Each set of 120 geometrical elements consists of 5 sets of 24. Each "half" of the 2-dimensional Sri Yantra (in the sense defined here) corresponds to a 600-cell, every geometrical element corresponding to one of the 120 vertices in the latter. The 240 geometrical elements formally correspond to the 240 vertices of the compound of two 600-cells, which is the Petrie projection of the 240 vertices of the 421 polytope. Each of the 5 sets of 24 geometrical elements in one half of the Sri Yantra is the counterpart of one of the 5 24-cells of which the 600-cell is a compound. The Sri Yantra is a 2-dimensional representation of the roots of E8 appearing in E8×E8 heterotic superstring forces. Each set of 24 geometrical elements is the counterpart of the 24 E8 gauge charges spread along each half-revolution of the 10 whorls of the UPA/superstring. The two halves of the Sri Yantra, each with 120 geometrical elements, correspond to the inner and outer halves of the UPA.
Surrounding the centre are 42 triangles with 126 sides, i.e., 168 geometrical elements. This leaves their 68 corners, the 3 sides of the central "triangle" (see, however, the caveat in the footnote for the commentary on the previous diagram) and the light blue corner below the bindu, i.e., 72 geometrical elements. The distinction between the four unshared geometrical elements at the centre of the Sri Yantra and the surrounding 168 elements generates a 72:168 division that is characteristic of sacred geometries (see The holistic pattern). It expresses the division of the 240 roots of the exceptional Lie group E8 into the 72 roots of E6 (one of its exceptional subgroups) and its remaining 168 roots.

Hexagonal yod populations of the faces of the five Platonic solids
|
Platonic solid |
Edges |
Faces |
Hexagonal yods |
Hexagonal yods on edges | Hexagonal yods on interior sides |
Total |
|
Tetrahedron |
6 |
4 |
4×3 = 12 |
6×2 = 12 |
4×6 = 24 | 48 |
|
Octahedron |
12 |
8 | 8×3 = 24 | 12×2 = 24 | 8×6 = 48 = 2×24 | 96 |
|
Cube |
12 |
6 |
6×4 = 24 |
12×2 = 24 |
6×8 = 48 = 2×24 | 96 |
|
Subtotal |
30 |
18 |
60 |
60 |
120 | 240 |
|
Icosahedron |
30 |
20 |
20×3 = 60 |
30×2 = 60 |
20×6 = 120 | 240 |
|
Subtotal |
60 |
38 |
120 | 120 | 240 | 480 |
| Dodecahedron | 30 | 12 | 12×5 = 60 | 30×2 = 60 | 12×10 = 120 | 240 |
| Total | 90 | 50 | 180 | 180 | 360 | 720 |
The tetrahedron, octahedron & cube have 240 hexagonal yods in their faces when they are constructed from tetractyses (see last pink cell). As shown in the table on #2 in the discussion of the Platonic solids, they comprise 120 red hexagonal yods that either line edges or are located at the centres of tetractyses and 120 turquoise hexagonal yods that line internal sides of tetractyses. The 240 hexagonal yods consist of 10 sets of 24 hexagonal yods made up of two groups of 5 sets of 24 yods. One group comprises 5 sets of 24 red hexagonal yods, shown in the red, orange, yellow, green & blue cells. The other group consists of 5 sets of 24 turquoise hexagonal yods, shown in the 3 turquoise cells. There are 24 turquoise hexagonal yods in each half of the octahedron and in each half of the cube.

5 sets of 24 vertices & edges in each half of the disdyakis triacontahedron surround its axis.
Five sets of 24 geometrical elements in each half of the disdyakis triacontahedron surround its axis
The disdyakis triacontahedron is the polyhedral version of the inner Tree of Life. It has 62 vertices of 3 types: A (×30), B (×12) & C (×20). It has 180 edges and 120 triangular faces. Surrounding an axis passing through two diametrically opposite vertices are 60 vertices and 180 edges, i.e., 240 vertices & edges. When the axis passes through two opposite B vertices, they can be divided into 10 identical sets of 24 vertices & edges. This is not possible for axes passing through a pair of diametrically opposite A or C vertices because neither the number of A vertices (28) nor the number of C vertices (18) that, respectively, surround these axes is divisible exactly by 10. Each half of the disdyakis triacontahedron comprises 5 sets of 24 geometrical elements (3 A, B, 2 C, 6 AB, 6 BC & 6 CA). Each half is the polyhedral analogue of the 5 24-cells in a 600-cell, each with 24 vertices. The two halves of the disdyakis triacontahedron are the counterpart of the pair of 600-cells and their 5 sets of 24 vertices & edges surrounding an axis passing through two opposite A vertices are the counterpart of the fact that a 600-cell is a compound of 5 24-cells, each with 24 vertices.