| << Previous 1... 5 6 [7] 8 9 ...24 Next >> |
7. The Pythagorean musical counterpart of the disdyakis triacontahedron & the compound of two 600-cells determining E8
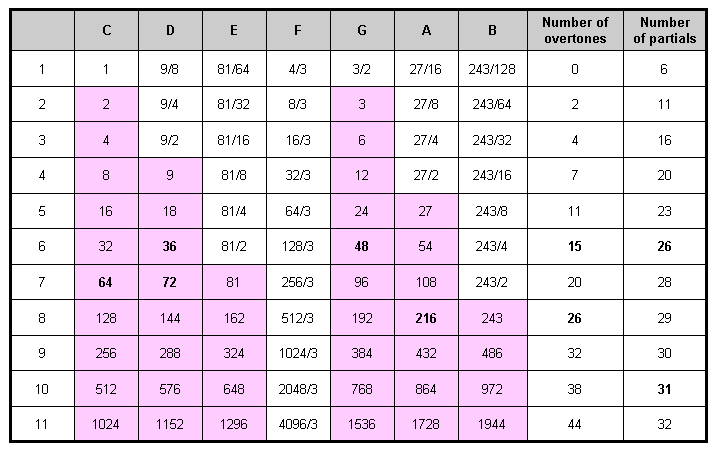
Table 1 lists the tone ratios of the first 11 octaves of the Pythagorean musical scale.
Table 1. Table of tone ratios of the first 11 octaves of the Pythagorean musical scale.
(overtones are in pink cells)

The note G6 with tone ratio 48 is the perfect fifth of the sixth octave. It is the 40th note, the 14th overtone and the 15th harmonic of the Pythagorean scale. The next harmonic (not a note of this scale) has tone ratio 49. EL CHAI, which is the Godname of Yesod with number value 49, determines the first of 1680 harmonics above G6 up to the note A11 with tone ratio 1728. Inspection of Table 1 confirms that A11, which is the first note in the Pythagorean scale to have a tone ratio larger than 1680, is also the only note differing by 1680 harmonics from a note of lower pitch. G6 and A11 are the only notes in any octave of the Pythagorean scale whose tone ratios differ by 1680. The significance of the uniqueness of this pair of notes is that it eliminates the criticism that any discussion based upon a particular choice of pairs of notes would be ad hoc if other pairs existed that differ by 1680. The 1680 harmonics 49−1728 above G6 up to A11 (840 even harmonics 50–1728; 840 odd harmonics 49–1727) comprise 240 harmonics up to D9 with tone ratio 288, namely, 120 even harmonics 50−288 and 120 odd harmonics 49–287, and 1440 harmonics above D9 up to A11, namely, 720 even harmonics 300–1728 and 720 odd integers 289−1727. Hence, the 1680 harmonics conform to the divisions:
1680 = 840 + 840,
840 = 120 + 720,
i.e.,
1680 = 720 + (120+120=240) + 720,
found earlier to be displayed by examples of sacred geometries. A11 is the 36th note, counting from A6, whilst it is the 31st note other than octaves. This is how the Godname ELOHA with number value 36 and the Godname EL with number value 31 pick out the 24th overtone above G6. Counting from the first note of the first octave, A11 is the 76th note, showing how it is picked out by the Godname YAHWEH ELOHIM with number value 76. Students of the Masonic number 33 will be pleased to discover that A11 is the 33rd overtone other than octaves! The note with tone ratio 54 is the lowest of the 24 overtones other than octaves that are amongst the 1680 harmonics up to A11. As the 15th overtone (see Table 1), it is picked out by the Godname YAH with number value 15.
In order to demonstrate that the 1680 harmonics between the two notes G6 and A11 really do constitute a holistic pattern, as their prescription by these Godnames indicate, let us, firstly, compare them with the 1680 geometrical elements that surround any axis of the disdyakis triacontahedron.
Disdyakis triacontahedron
If the former truly constitute a holistic set, their composition should correlate with the
geometrical structure of this polyhedron, which many research articles posted by the author to this website have
confirmed is the polyhedral form of the outer Tree of Life. When its axis passes through two diametrically
opposite A vertices, the 1680 elements comprise 24 vertices above the 12-gon in the central plane of the
polyhedron, 24 vertices below it, 12 vertices of this 12-gon and 180 vertices of the 540 internal triangles, i.e.,
240 vertices. Their musical counterparts are the 24 harmonics beyond G6 up to
D7 (Table 1), then 24 harmonics beyond D7 up to G7, 12 more harmonics to
A7 (the first of the five octaves spanned by the 24 overtones above G6 up to
A11 — see later in this paragraph — and the 21st
Table 2. Geometrical counterparts of the 24 overtones between G6 and A11.

Pythagorean harmonic) and the next 180 harmonics up to D9 (the 240th harmonic above G6), which, as the perfect fourth of the third of these octaves, is the middle of the five octaves. Then, there are 180 edges, 60 internal sides ending on polyhedral vertices & 120 external triangles, i.e., 360 edges/sides & triangles. Their Pythagorean musical counterpart is the 360 harmonics beyond D9 up to E10. Finally, there are 540 more internal edges of 540 internal triangles, i.e., 1080 internal edges & triangles. Their counterpart is the 1080 harmonics above E10 up to A11. Table 2 opposite displays the 24 overtones other than the five octaves above G6, i.e., the non-trivial overtones. Notice that the 240:1440 division is marked by note D9 with tone ratio 288, i.e.,
288 = 48 + 240 = 11 + 22 + 33 + 44.
This manifests in the 288 yods surrounding the centres of the seven regular polygons of the inner Tree of Life as their 48 corners and 240 hexagonal yods. The overtone A6 with tone ratio 54 is the first of the overtones included in the 1680 successive harmonics. The overtone A11 with tone ratio 1728 is the last one. Their ratio = 32 = 25, i.e, the overtones from A6 to A11 span five octaves, the note D9 being their midpoint. So this note demarcates 240 harmonics from the remaining 1440. This manifests in the disdyakis triacontahedron as the 240 vertices/corners of its external & internal triangles and as its 1440 edges/sides & triangles. The 120 even harmonics and 120 odd harmonics correspond to the 120 corners of the 330 triangles in either the faces (30 vertices) or the interior (90 corners) of each half of the polyhedron.
Next, let us compare the 1680 harmonics with the 1680 vertices & edges in the two 600-cells whose compound is the 4-dimensional projection in the Coxeter plane of the Gosset polytope whose 240 vertices determine the 240 root vectors of the exceptional Lie group E8 used in E8×E8 heterotic superstring theory.
Compound of two 600-cells
This has 240 vertices and 1440 edges, i.e., 1680 vertices & edges. The 120 vertices in one 600-cell correspond
to the 120 even harmonics 50–288 and the 120 vertices in the other 600-cell correspond to the 120
odd harmonics 49–287. Their 1440 edges correspond to the 1440 harmonics above
D9 up to A11, the 720 edges in one 600-cell corresponding to the 720 even harmonics and
the 720 edges in the other 600-cell corresponding to the 720 odd harmonics. Notice that the 240 harmonics comprise
24 harmonics up to D7 and another 24 harmonics up to G7. They correspond in the
disdyakis triacontahedron to the 24 vertices either above or below its central 12-gon perpendicular to an A-A axis
and to the 24 vertices of a 24-cell in each 600-cell. Notice also that, just as the 24 overtones
A6–A11 span five octaves, so that there are five 24-cells in each 600-cell.
|
|
|
| A 4×4 square array of the cubes of the first 4 odd
integers expresses the geometrical composition of CTOL |
49 Trees of Life have 1680 geometrical elements and CTOL has 3108 geometrical elements. |
The counterpart in the UPA of this five-fold character is the five revolutions of each helical whorl with 1680 turns. Each of the five octaves is analogous to one of its five revolutions. Note, however, that the 24 overtones within the 1680 harmonics span five octaves, not the 1680 harmonics themselves. The middle of the five octaves marks the change for the geometries of the two 600-cells and the disdyakis triacontahedron from points in space to, respectively, lines and lines & triangles. The counterpart of this in the UPA is the fact that the outer and inner halves of each whorl make 2½ revolutions around its axis, the bottom of the UPA being the half-way point of a whorl. However, the number of harmonics spanning an octave doubles with successive octaves. The number of harmonics in successive octaves = 60, 168, 384, 816 & 1680. Their sum = 3108 = 14 + 34 + 54 + 74. Amazingly, this is the number of points, lines & triangles that make up the 91 overlapping Trees of Life in CTOL (see also here). Not only that, the number 1680 is the number of geometrical elements in 49 overlapping Trees of Life!* This is the Tree of Life representation of the 49 subplanes of consciousness of the cosmic physical plane (see here). So the 1680 harmonics up to the last of the 24 overtones other than octaves of the Pythagorean scale correspond to the number of geometrical elements needed to construct the 49 Trees mapping the cosmic physical plane, whilst the sum of the numbers of harmonics making up the five successive octaves of overtones A7, A8, A9, A10 & A11 is the number of geometrical elements in CTOL itself. The association is very appropriate because the number 168 is the number of Cholem Yesodoth, the Mundane Chakra of Malkuth and the cosmic physical plane corresponds to this Sephirah on a cosmic scale, whilst, as a subquark state of the E8×E8 heterotic superstring, the UPA is the basic unit of physical matter. The average increase per octave in the number of harmonics = 1680/5 = 336, which is the number of turns in each revolution of a helical whorl of a UPA. In the analogy between the Pythagorean scale and each whorl, an octave corresponds to a complete 360° revolution of the latter around the axis of the spinning UPA and each harmonic corresponds to a circular turn. The 24 overtones that are not octaves correspond to the 24 E8 gauge charges associated with each set of 1680 turns (either a whorl or a half-revolution of all 10 whorls).
Table 3 compares the properties of the 1680 harmonics, the 1680 geometrical elements surrounding an A-A axis of the disdyakis triacontahedron and the 1680 vertices & edges of the two concentric 600-cells whose compound is the 4-dimensional, Coxeter plane projection of the 240 vertices of the 421 polytope. Each harmonic has its counterpart in a geometrical element surrounding an axis of the disdyakis triacontahedron or in a vertex or edge of the two 600-cells.
Table 3
|
Harmonics of the Pythagorean scale (G6–A11) |
Surrounding an A-A axis of the disdyakis triacontahedron |
Compound of two 600-cells |
|
| G6–D7: 24 | 24 vertices above central plane. | 24 vertices of a 24-cell in 1st 600-cell. | |
| D7–G7: 24 | 24 vertices below central plane | 24 vertices of a 24-cell in 2nd 600-cell. | |
| G6–D9: 240 | 120 even | 120 points (30 vertices, 90 corners of internal triangles) in upper half. | 120 vertices of 1st 600-cell. |
| 120 odd | 120 points (30 vertices, 90 corners of internal triangles) in lower half. | 120 vertices of 2nd 600-cell. | |
| D9–A11: 1440 | 720 even | 720 sides & triangles in upper half. | 720 edges of 1st 600-cell. |
| 720 odd | 720 sides & triangles in lower half. | 720 edges of 2nd 600-cell. | |
| G6–A11: 1680 | 840 even | 840 geometrical elements in upper half. | 840 vertices & edges of 1st 600-cell. |
| 840 odd | 840 geometrical elements in lower half. | 840 vertices & edges of 2nd 600-cell. | |
There are 1680 geometrical elements surrounding an axis of the disdyakis triacontahedron, through whatever pair of diametrically opposite vertices it passes. However, only when these two vertices are A vertices does the correlation between its geometrical composition and the harmonics extend to the two sets of 24 harmonics in the first of the octaves formed by the overtones above G6. This is because 24 vertices surround an axis both above and below the central plane of this polyhedron only when the axis perpendicular to this plane passes through two opposite A vertices, not B or C vertices.
We found at the end of #4 that the 24-cell with Type B triangles as its faces and internal triangles formed by its edges has 1728 simple triangles. Because this polychoron has the same number of faces and edges, it has 864 internal triangles and 864 triangles in its faces. Inspection of Table 1 shows that A10 has the tone ratio 864 and is separated by 864 harmonics by its next higher octave A11 with tone ratio 1728.
The section "1680 = 840 + 840" in The holistic pattern under the heading "Pythagorean scale (the musical connection with the superstring)" discusses in more detail the unique existence of two notes in the Pythagorean musical scale that are separated by 1680 harmonics.
Such correspondences with both the Pythagorean scale and the disdyakis triacontahedron are further confirmation that the compound of two 600-cells embodying the structural parameter 1680 of the UPA constitutes real sacred geometry. To discount all these parallels as due to coincidence is to entertain the absurd notion of a miraculous improbability.
*Proof: n overlapping Trees of Life have (12n+4) triangles with (6n+4) corners and (16n+6) sides, i.e., (34n+14) geometrical elements. The number of geometrical elements in CTOL (n=91) = 34×91 + 14 = 3108. 49 overlapping Trees have (34×49 + 14 = 1680) geometrical elements.
| << Previous 1... 5 6 [7] 8 9 ...24 Next >> |