Home
4. The sacred-geometrical character of the
24-cell
The 24 vertices of each of the (5+5) 24-cells making up the compound of two 600-cells whose 240
vertices determine the 240 root vectors of E8 denote gauge charges of this Yang-Mills gauge
symmetry group. These charges are spread along each of the (5+5) half-revolutions of all 10 whorls of the UPA as
the subquark state of the E8×E8 heterotic superstring. The 24-cell is unique amongst
n-polytopes (n≥4) in being the only one other than the n-simplex that is self-dual. In fact, it is holistic, too,
for the following reason: the 24-cell has 24 vertices, 96 edges, 96 triangular faces & 24 octahedral cells. Its
0-, 1-, 2- & 3-polytopes comprise 120 vertices & edges and 120 faces & cells. This 120:120 division of
its 240 polytopes is characteristic of holistic systems, as, of course, is its embodiment of the holistic parameter
240. It is a repetition of the archetypal pattern discussed earlier in the compound of two 600-cells, each with 120
vertices, and in other sacred geometries previously compared with them. Its polytope composition conforms to the
hexagonal yod composition of the seven regular polygons making up the inner form of the Tree of Life, as shown
below:
 |
 |
|
The 24-cell consists of 240 polytopes:
24 vertices;
96 edges;
96
triangles;
24 octahedral cells.
|
Constructed from tetractyses, the 7 separate polygons of the inner
Tree of Life have 240 hexagonal yods:
The triangle, square,
pentagon & dodecagon have 120 hexagonal yods. They comprise 24 dark red hexagonal yods at the
centres of 24 tetractyses and 96 blue hexagonal yods on their sides. The former correspond to the
24 vertices of the 24-cell and the latter correspond to its 96 edges.
The hexagon, octagon & decagon have 120 hexagonal yods.
They comprise 24 light red hexagonal yods at centres of tetractyses and 96 green hexagonal yods on
their sides. The former correspond to the 24 octahedral cells in the 24-cell and the latter
correspond to its 96 triangular faces.
|
(See also the discussion on #1 (see under heading "24-cell") of other properties of
the 24-cell that indicate its holistic character, e.g., the 384 sides of the simple triangles in its faces when
they are Type A). Further evidence that the 24-cell has a holistic character is the fact that the 120:120
division of its polytopes mirrors the 120:120 division of the 240 geometrical elements surrounding the centres
of the two Type B dodecagons in the inner Tree of Life, each dodecagon corresponding to half of the 24-cell:
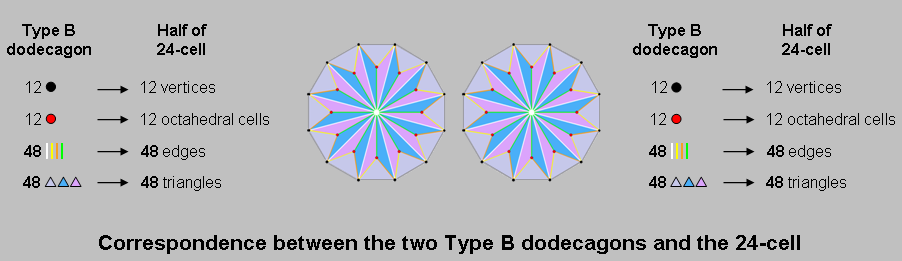
Their 24 black corners correspond to the 24 vertices of the 24-cell, the 24 red corners of their
72 triangles correspond to its 24 octahedral cells, the 96 interior sides of their triangles
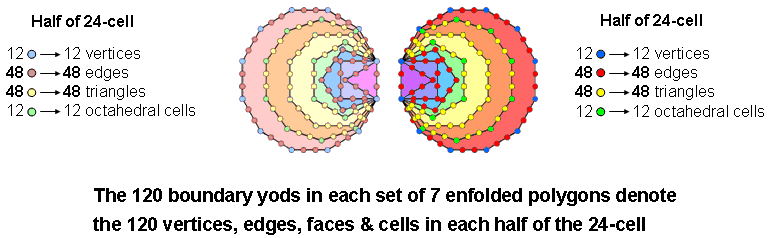
correspond to its 96 edges and the 96 sides & triangles correspond to its 96 triangles. The same 24:96:96:24
pattern is found in the 240 boundary yods of the two separate sets of seven enfolded polygons, each
set representing half the 24-cell:
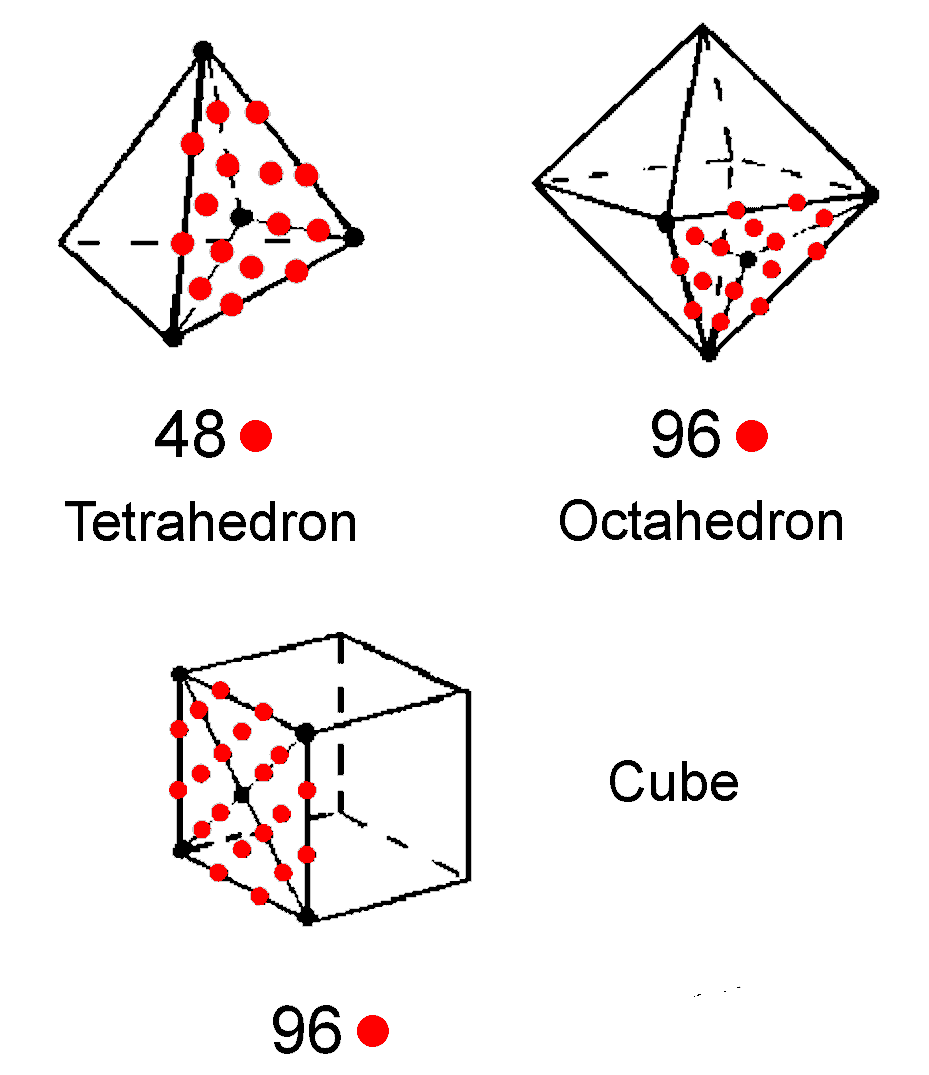
It also occurs in the 240 hexagonal yods in the faces of the tetrahedron, octahedron & cube
when they are constructed from tetractyses:
 |
|
Platonic
solid
|
Edges |
Faces
|
Hexagonal yods at centres
|
Hexagonal
yods on edges |
Hexagonal yods
on interior sides |
Total |
|
Tetrahedron
|
6
|
4
|
4×3 = 12 |
6×2 = 12
|
4×6 = 24 |
48 |
|
Octahedron
|
12
|
8 |
8×3 = 24 |
12×2 = 24 |
8×6
= 48 |
96 |
|
Cube
|
12
|
6
|
6×4 = 24
|
12×2 = 24
|
6×8 = 48 |
96 |
|
Total
|
30
|
18
|
60 |
60
|
120 |
240 |
|
The 120 hexagonal yods either at their centres or on their edges comprise (12+12=24) in the
tetrahedron and (24+24+24+24=96) in the octahedron & cube (indicated in the red cells); the 120 hexagonal yods
lining interior sides of tetractyses in their faces comprise 24 in the tetrahedron and
(48+48=96) in the octahedron & cube (shown in the blue cells). It cannot be
accidental that there is such repetition of this pattern in objects like the inner Tree of Life, the dodecagon and
the Platonic solids — objects which have been previously established as possessing sacred geometry because they
exhibit its defining parameters and display the same patterns that relate them. Rather, its re-occurrence in the
24-cell points towards the holistic character of this polychoron and confirms its connection to both
superstring physics and the structure of the UPA.
As
24 = 52 − 1 = 3 + 5 + 7 + 9
is the sum of the first four odd integers after 1 and
120 = 112 − 1 = 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 +
21,
is the sum of the first 10 integers after 1, we see that the Pythagorean Tetrad and Decad
determine both numbers and their difference:
96 = 120 − 24 = 11 + 13 + 15 + 17 + 19 + 21.
The 24 vertices (or octahedral cells) and 96 edges (or triangles) possessed by the 24-cell
follows the arithmetic pattern of the first four and the last six odd integers in the first 10 odd integers! This
4:6 division parallels the prediction by superstring theory that space-time has 10 dimensions, of which four form
the large-scale Minkowski space-time continuum and six are compactified.
The question next to be asked is: given that a 24-cell determines 24 E8 gauge
charges that are spread along a half-revolution of all 10 whorls of the
UPA/E8×E8 heterotic superstring around its axis of spin, i.e., 1680 turns of these
helices, how does the polychoron generate this winding number as a component of the 10 24-cells whose 240 vertices
define the roots of E8? Each charge is spread uniformly over 70 turns in a half-revolution of all 10
whorls, seven per whorl, so that the three major whorls have 21 such turns and the seven
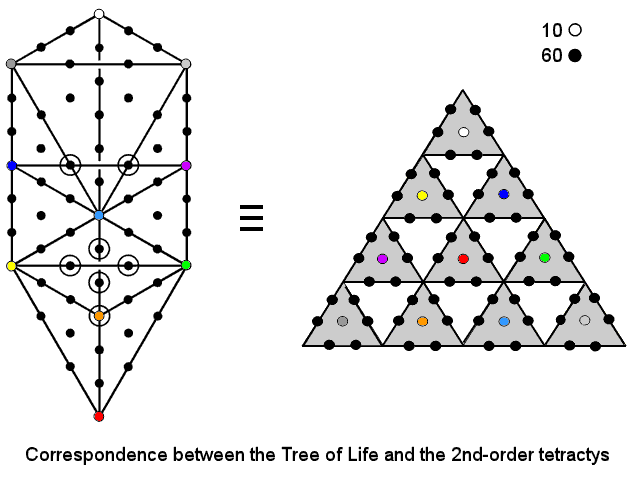
minor whorls have 49 such turns. This number is highly significant vis-à-vis the Tree of Life
because its 16 triangles have 70 yods when they are tetractyses (see here). This identification is consistent with the 2nd-order tetractys and
the distinction between the three major and seven minor whorls of the UPA because the
(21+49=70) hexagonal yods in the (3+7=10) 1st-order tetractyses of the
2nd-order tetractys consist of 10 sets of seven hexagonal yods. It would represent an E8 gauge
charge, the 70 yods denoting 70 turns in 10 whorls, each 1st-order tetractys denoting a half-revolution of a
single whorl and the seven hexagonal yods in each 1st-order tetractys symbolising the seven turns per whorl:
 |
 |
It is well-known that the chromatic number for a graph drawn on a 2-torus T2 is 7. The polychorons
have an Euler characteristic of 0. This happens to be the same as the Euler characteristic of an n-dimensional
torus Tn, which is the product space of n circles. This is precisely how Leadbeater described the
six orders of circular turns higher than the ones making up each whorl of the UPA. Given that the 240
E8 gauge charges are the sources of 10-dimensional gauge fields, it is as though they are spread
along the 10 whorls, 120 in each inner or outer half corresponding to the 120 vertices of each 600-cell, and
that each whorl (or, rather, seven turns in a whorl) generates a space-time component of each gauge field:
16800 turns in 10 whorls ≡ 240 E8 gauge charges × 10 space-time components of
E8 gauge field ×7.
7 turns ≡ space-time component of E8 gauge field.
This, however, is still a speculation that needs to be proved or disproved because the
mathematical connection between this chromatic number and the 10-fold subquark state of the
E8×E8 heterotic superstring needs yet to be established. But it is clear that sections
of seven turns in each whorl have holistic significance, for C.W. Leadbeater stated that every circular turn was
comprised of seven coils that wound around a smaller circle, and that each coil was a helix made up of seven still
smaller coils, and so on. This means that the six higher orders of what he called "spirillae" (see here) represent the winding of a curve around six successively smaller
circles, all mutually orthogonal, i.e., the six compactified, circular dimensions of the 6-torus T6.
Whatever is responsible for a 7-fold winding around each compactified dimension (obviously connected to the
chromatic number 7 for a 2-torus) is responsible for an analogous winding around every seven circles making up a
whorl wound on a 2-torus. It is highly significant that he should have counted seven coils of the next higher
order making up a coil of a given order in a minor whorl. This establishes a connection between his counted
number (1680) of turns in a whorl and the group-theoretical number 240 of roots in the Lie group
E8:
1680 = 240×7.
It indicates that, indeed, sections of seven turns — to whatever order of spirilla they belong —
do represent physically significant things, in this case (if the above interpretation is correct) the
space-time component of a gauge field of E8. The question that needs answering is why the
168 helical turns in each half-revolution of a whorl are the string manifestation of 24
E8 gauge charges. It is like the question: why are there 24 hours in a day and a week
of seven days with 168 hours? Is the re-appearance of these numbers no more
than a coincidence? Or are they a reflection of the existence of a fundamental cosmic cycle that happened to be
reproduced in ancient times when, firstly, the ancient Egyptians used the practice in the earlier Sumerian culture
of counting with their thumb against the three knuckles of the other four fingers to divide the day (and then the
night) into 12 parts that only became equal in ancient Greece under the influence of its great astronomer
Hipparchus and, secondly, the creation myths of Judaism and ancient Babylonian religions gave rise to a seven-day
week based upon seven stages of creation? If the UPA exists as 10 whorls because superstring space-time is
10-dimensional, then its three major whorls bear a formal correspondence to the three large-scale dimensions and
its seven minor whorls correspond to the six compactified dimensions and the dimension of time, so that the
breakdown in the unified symmetry of E8 arising from the difference of scale between these two
classes of dimensions led to a difference between three whorls that generate the three components of the gauge
fields in large-scale space and the remaining seven whorls. This is what Leadbeater noticed in the UPA, for three
whorls, which he called "major," were thicker than the seven other "minor" ones (see here for the reason for this difference). The difference, of course, in
Kabbalistic terms is that between the Supernal Triad of Kether, Chokmah & Binah and the seven Sephiroth of
Construction. In Pythagorean terms, it is the difference between the yods at the three corners of the tetractys
and its seven hexagonal yods (see here).
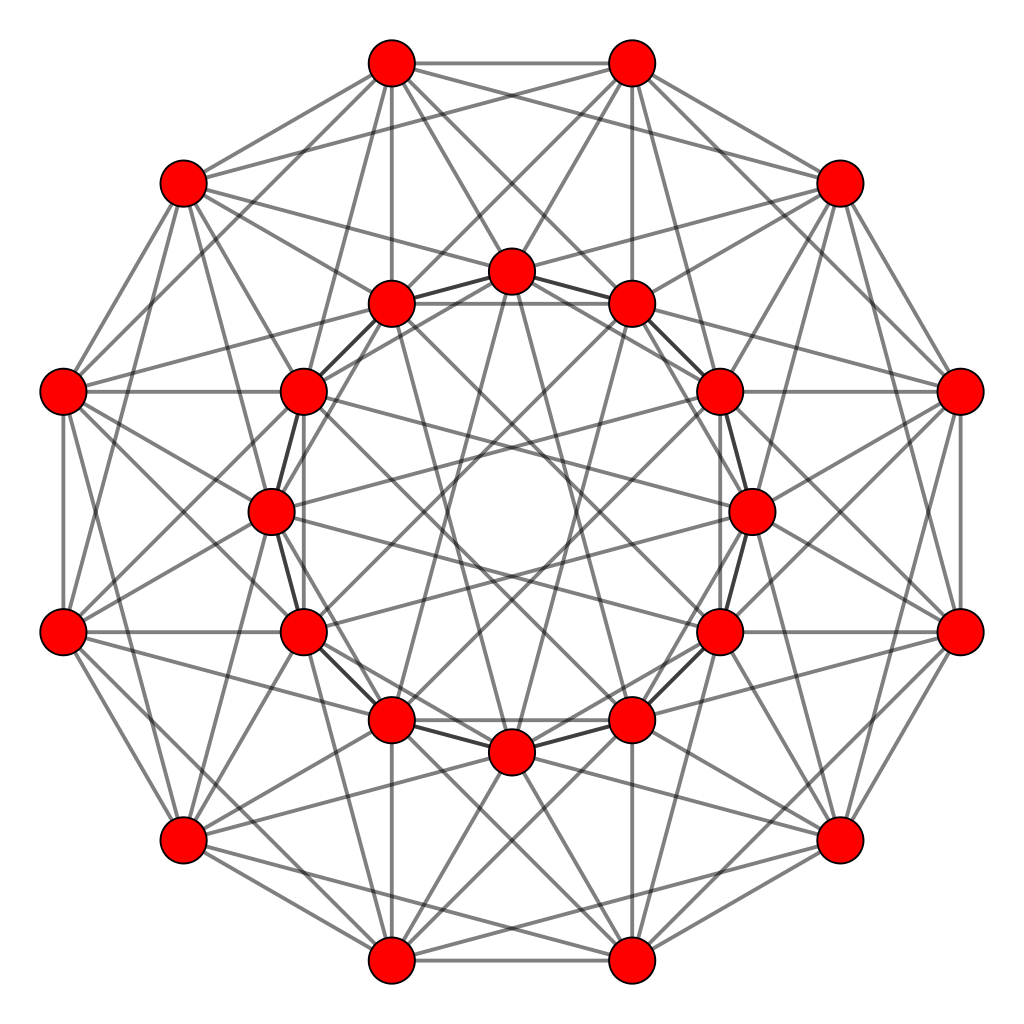
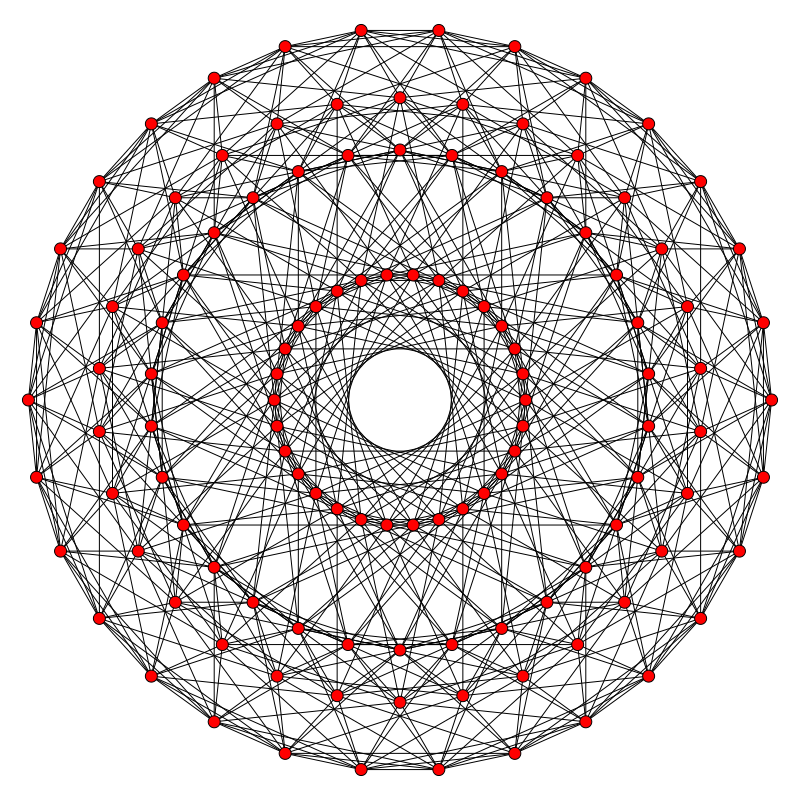
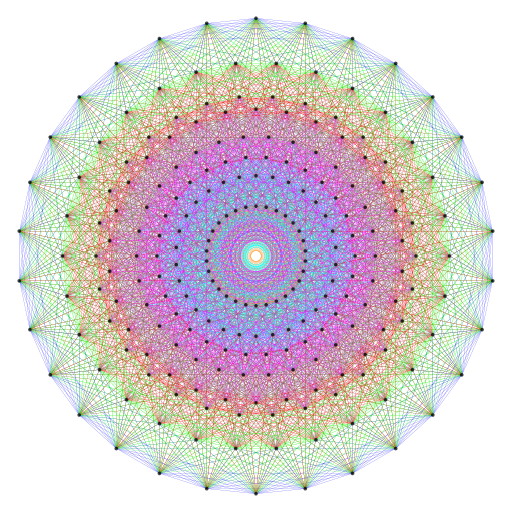
Shown below are the Petrie polygons of the 24-cell, the 600-cell and the
421 polytope:
 |
 |
 |
|
Petrie polygon of the 24-cell is the dodecagon
|
Petrie polygon of the 600-cell is the triacontagon
|
Petrie polygon of the 421 polytope is the triacontagon
(To enlarge, place mouse pointer over image)
|
|
×5 →
|
×2 →
|
|
The Petrie polygon of the 24-cell is the dodecagon, which is the last of the seven regular
polygons making up the inner Tree of Life. The Petrie polygon of the 600-cell, a compound of five 24-cells, is the
regular 30-gon, as is the Petrie polygon of the 421 polytope because it is a compound of two
concentric 600-cells of different size but with the same orientation. As 30/12 = 2½, the factor of 5 between the
120 vertices of the 600-cell and the 24 vertices of the 24-cell manifests in the repetition of the outermost two
circular rows of 30 vertices in the Petrie polygon of the former. The factor of 10 between the 24 vertices of the
24-cell and the 240 vertices of the 421 polytope arises from the repetition of the four outermost
circular rows of 30 vertices in the four innermost circles. Remarkably, comparison of the Petrie polygons of the
24-cell and the 421 polytope reveals the same ×10 and ×2½ factors as those
manifesting in the UPA, namely, the 10 half-revolutions of its whorls (or the 10 whorls) and the 2½ revolutions in
its inner or outer halves. For the unbelieving sceptic, this has to be dismissed as just another coincidence, along
with the (840+840=1680) vertices & edges of the two 600-cells, whose embodiment of the structural parameter
1680 can be for such a person no more than the product of chance. However, for those who do not believe in
miracles, the presence of the factors 2½, 5 & 10 in the Petrie polygon of the 600-cell makes the embodiment in
its geometry of the UPA structural parameter 840 all the more significant, providing yet more compelling evidence
that this particle remote-viewed over a century ago is the E8×E8 heterotic superstring.
At the same time, it must be pointed out that the 421 polytope occupies 8-dimensional space,
whereas the features of the UPA being compared to it or to its 4-dimensional, Coxeter plane projection pertain to
3-dimensional space. Even though the two spaces are different, it should not be hard to accept that the features
that pertain to the space occupied by a polychoron representation of the E8 roots/gauge charges
carried by a superstring should also apply to their manifestation in the 4-dimensional cross-section of
10-dimensional space-time.
Here is another reason why we should take seriously these correspondences between mathematical
facts, sacred geometrical patterns and alleged paranormal descriptions of the basic unit of matter. The dodecagon
needs 168 more yods to transform its 12 sectors into Type A triangles, turning into a Type B
dodecagon:
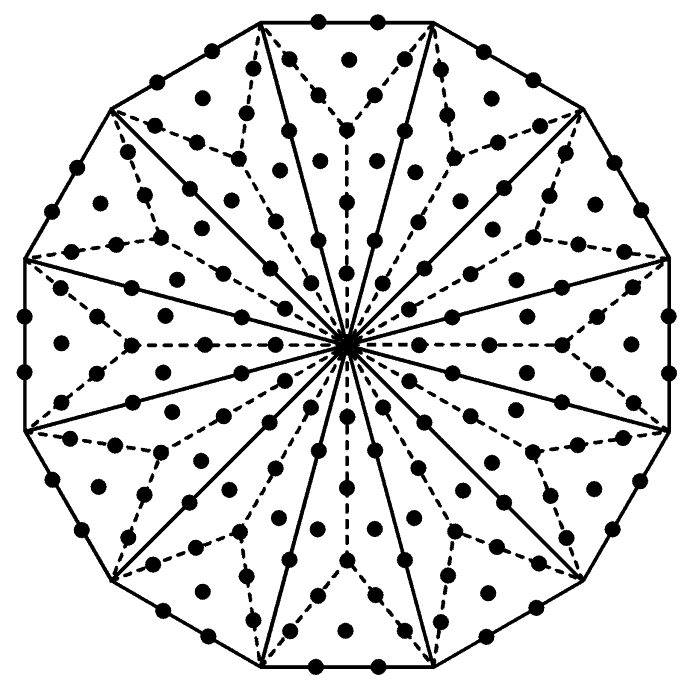
Notice that this regular polygon is the Petrie polygon of the 24-cell. Might we not
expect, therefore, that the 24-cell has a connection to the number 1680 — the number of turns in a
half-revolution of the 10 helical whorls of the UPA that, according to our earlier analysis, "carries" 24
E8 gauge charges denoted by the vertices of this polychoron? Yes, as now explained. Taking the edge
length of the 24-cell as 1, eight of its vertices have coordinates that are all the permutations of (±1, 0, 0, 0);
they are vertices of the 16-cell:
|

Rotating 16-cell.
|
Petrie polygon of the 16-cell.
|
Isometric Orthogonal Projection of:
8-Cell (Tesseract) + 16-Cell = 24-Cell
Credit:
Title: Cell24Construction.ogv
Author: Jgmoxness
|
|

|
|
| |
|
Rotating 8-cell.
|
Petrie polygon of the 8-cell.
|
|
16 vertices of the 24-cell are of the form: (±½, ±½, ±½, ±½); they are the vertices of an
8-cell. They can be divided into two groups of eight: those with an even number of (−) signs and those with an odd
number of (−) signs. Each group of vertices defines a 16-cell. Therefore, the 24 vertices of a 24-cell can be
grouped into three sets of eight, each set defining a regular 16-cell. According to Table 2 on #1, the 16-cell is composed of 168 triangles when
its faces and interior are constructed from Type A triangles, whilst the 24-cell comprises 576 triangles, where
576 = 242. Here, therefore, is a mathematical connection between the superstring structural parameter
168 and the 24-cell. According to comment (1) about the 8-cell on #1, 168 points & lines compose its 24 square
faces. This is analogous to the 1680 vertices & edges making up the 2400 faces in the compound of two
600-cells that is the Petrie projection of the 421 polytope. We see that this number (the
gematria number value of Cholem Yesodoth, the Mundane Chakra of Malkuth) manifests as
well in both the 8-cell and the 16-cell that make up each of the 10 24-cells in this compound. In view of this,
it should come as no surprise that the 24-cell plays a central role in the complete, superstring explanation of
the 10 whorls of the UPA ....
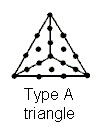
The 24-cell constructed from Type A triangles
We saw earlier that the 240
hexagonal yods in the seven regular polygons making up the inner Tree of Life symbolise the 240 0-, 1-, 2- &
3-polytopes in the 24-cell. Additional confirmation of its holistic character is provided by its construction from
Type A triangles:
 |
 |
The 24-cell has:
24 vertices
96 edges
96 triangular faces
24 octahedra
Numbers of geometrical elements other than vertices & edges surrounding centre of
24-cell
| |
Corners |
Sides |
Triangles |
Total |
| Faces |
96 |
3×96=288 |
3×96=288 |
672 |
| Interior |
96 |
24 + 3×96 = 312 |
3×96=288 |
696 |
| Total |
192 |
600 |
576 |
1368 |
|
 |
| |
Rotating 24-cell |
|
1368 yods are intrinsic to the (7+7) Type B polygons enfolded in each
overlapping Tree of Life |
When the 96 internal triangles formed by its edges and its 96 faces are Type A triangles, the
centre of the 24-cell is surrounded by 1368 corners, sides & triangles other than its 24 vertices and 96 edges.
In other words, given the latter, 1368 more geometrical elements are needed to construct the polytope. The inner
form of the Tree of Life with Type B polygons contains 1370 yods. Of these, the topmost corners of the two hexagons
coincide with the lowest corners of the hexagons enfolded in the next higher Tree of Life. This means that 1368
yods are intrinsic to each set of 14 enfolded Type B polygons. They denote the 1368 extra geometrical elements in
the 24-cell built both internally and externally out of Type A triangles. It demonstrates that this polytope
conforms to the holistic pattern of the inner Tree of Life. This is true also when the seven regular polygons are
separate, for the 672 extra geometrical elements in its faces comprise 96 corners, 288 sides & 288 triangles,
and these numbers are the extra corners, sides & triangles added when the (7+7) separate Type A polygons are
turned into Type B polygons:
corners: 48 +
48 = 96;
sides: 3×48 + 3×48 =
288;
triangles: 3×48 +
3×48 = 288.
Total = 672.
Each half of the 24-cell has 336 extra geometrical elements. There are (5×672=3360) extra
geometrical elements in the five 24-cells (1680 in each half), the compound of which is the 600-cell. The presence
of the three UPA structural parameters 336, 1680 & 3360 in the geometry of the 600-cell is strong confirmation
that the UPA is an E8×E8 heterotic superstring. There are 6720 extra geometrical
elements in the 10 24-cells making up the compound of two 600-cells. Compare this with the 3360 circularly
polarised waves in each revolution of the 10 whorls of the UPA. Each wave is a supposition of two plane waves with
a phase difference of 90°. Therefore, 6720 plane waves circulate once around the axis of the particle. It is hard
to resist the conclusion that they are the manifestation of the 6720 extra geometrical elements required to
construct the 10 24-cells from Type B triangles. This is particularly so given that the
421 polytope has 60480 faces with 240 vertices and 6720 edges! In other words, the very 8-dimensional polytope whose vertices determine the 240 root vectors of
E8 has exactly the same number of edges as:
-
the number of orthogonal plane waves that generate the 3360 circularly
polarised oscillations in one revolution of the 10 whorls of the UPA about its axis of
spin;
-
the number of geometrical elements generated by dividing into their sectors
the faces of the 10 24-cells in the compound of two 600-cells that is the 4-dimensional, Coxeter plane
projection of the 421 polytope.
Given that 672 extra geometrical elements are needed to divide the 96 faces of the 24-cell into
their 288 sectors, is it a coincidence that, as shown here, 672 yods are needed to construct the first four Platonic solids
from Type A triangles? Why should the 421 polytope, which mathematicians know reproduces the 240
root vectors of the exceptional Lie group E8 present in one of the two heterotic superstring
theories, have exactly ten times as many edges as these Platonic solids contain yods when they are
constructed from Type A triangles? Why, as pointed out on #2, should the number of yods (13680) lining the edges of the faces of
this polytope when they are tetractyses be exactly ten times the number of yods that are intrinsic
to the inner form of one Tree of Life with Type B polygons? Why should this number be exactly the
number of yods intrinsic to the inner form of ten overlapping Trees of Life? Either miraculous
coincidences are in play here or we are witnessing the remarkable appearance in different systems of geometry of
the same number simply because all these systems possess sacred geometry characterised by the same
parameters (apart from a Pythagorean factor of 10 in some cases). The reader must decide which is the more
plausible possibility.
Inner Tree of Life pattern of the 24-cell
When the 96 faces of the 24-cell
and the 96 internal triangles formed by its edges are Type A triangles, their (3×96 + 3×96 = 576) triangular
sectors have (1+24+96+96=1+216=217) corners, where "1" denotes the centre of the polychoron. The
number 216 of Geburah is the number of corners of triangles that surround the centre of the
24-cell. Compare this with the fact that, of the 264 yods in the seven enfolded Type A polygons with tetractyses as
their 47 sectors, (264−47=217) yods line the sides of the tetractyses. Of these, one yod at the topmost corner of
the hexagon coincides with the lowest corner of the hexagon enfolded in the next higher Tree, leaving
216 boundary yods that are intrinsic to the set of polygons enfolded in each Tree. The shared
corner, which is unique because it also belongs to another set of polygons, corresponds to the centre of the
24-cell and the 216 boundary yods of the sectors of the seven enfolded polygons correspond to
the 216 corners of the 576 sectors of the 192 Type A triangles from which the polychoron is
constructed. Notice also that (1 + 24×2 = 49) yods line the 24 sides of the 96
internal triangles formed by the edges of the 24-cell, where 49 is the number
of EL CHAI, the Godname of Yesod, and that (24 + 2×96 = 216) yods line the edges of the 24-cell —
just as they do for the sectors of the seven enfolded polygons. This correspondence is further evidence that the
24-cell conforms to the holistic pattern of the inner Tree of Life.
 |
Lining the 88 sides of the 47 tetractys sectors of
the 7 enfolded polygons are 216 yods, excluding the topmost corner of the hexagon that is shared with the hexagon enfolded in the
next higher Tree of Life. This is the number of yods on the 96 edges of the 24-cell when its
faces are tetractyses. 2160 yods line the 880 sides of the 470 tetractys sectors of the 70
polygons enfolded in 10 Trees of Life. This is the number of yods on the edges of the 10 disjoint
24-cells making up the compound of two 600-cells. A 24-cell is to a 600-cell what a single
Tree of Life is to 10 Trees representing its 10 Sephiroth. It indicates that the two
centre-sharing 600-cells are the 4-dimensional counterparts of the two sets of five Sephiroth — or,
rather, the two sets of five Trees of Life that represent them.
|
It suggests that we should carry out a more thorough analysis of the yod composition of
the 24-cell. Tabulated below is the numbers of yods in its faces and interior:
|
Face/internal triangle
|
Faces
|
Interior
|
Total
|
|
Corners |
Hexagonal yods |
Total |
Corners |
Hexagonal yods |
Total |
Corners |
Hexagonal yods |
Total |
| Tetractys |
24 |
96×2 + 96 = 288 |
312 |
1 |
24×2 + 96 = 144 |
1+144=145 |
1+24=25 |
432 |
1+456=457 |
| Type A triangle |
24+96=120 |
96×2 + 96×9 = 1056 |
1176 |
1+96=97 |
24×2 + 96×9 = 912 |
1+1008=1009 |
1+216=217 |
1968 |
1+2184=2185 |
| Type B triangle |
24 + 96×4 = 408 |
96×2 + 96×33 = 3360 |
3768 |
1 + 96×4 = 385 |
24×2 + 96×33 = 3216 |
1+3600=3601 |
1+792=793 |
6576 |
1+7368=7369 |
Comments
-
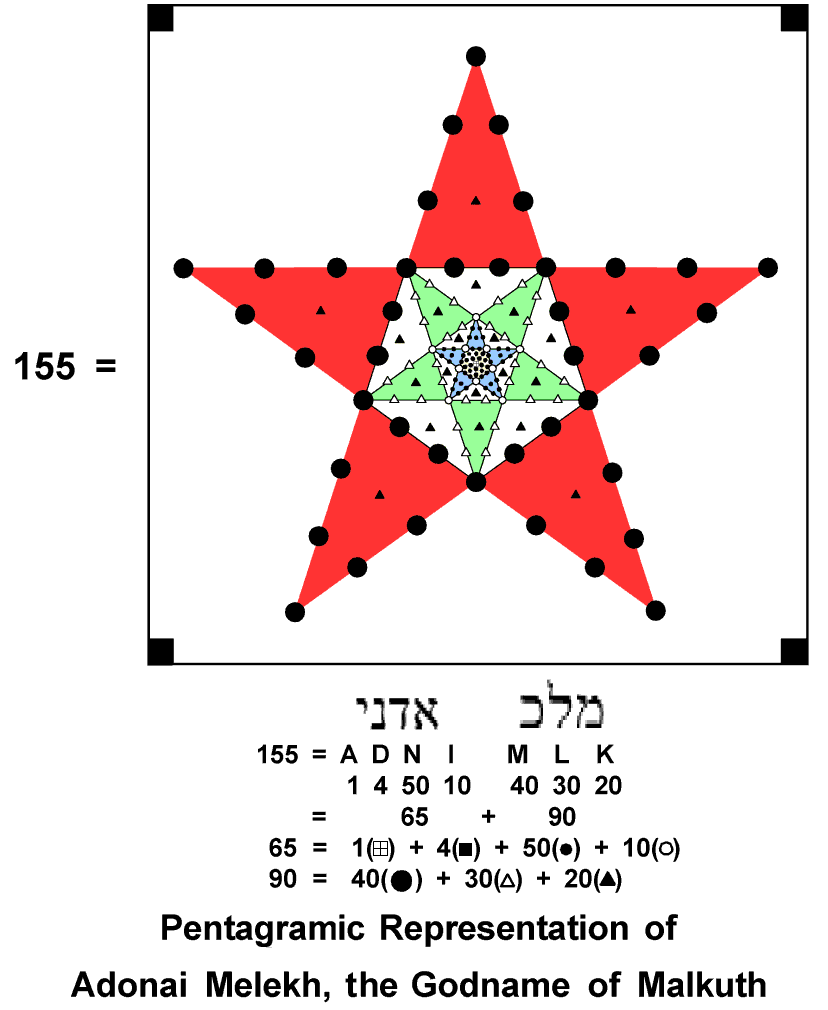
Its 96 faces are composed of 312 yods when they are tetractyses. 312 is the 155th even
integer after 2, the first even integer, where 155 is the number value of ADONAI
MELEKH, the Godname of Malkuth:
Each half of the 24-cell has 216 hexagonal yods, where
216 is the number of Geburah. There are 457 yods, of which 24 are vertices,
leaving 433 generated by the transformation of the faces into tetractyses. 433 is the 84th prime
number, where 84 = 12 + 32 + 52 + 72.
-
216 corners surround the centre when the faces are Type A triangles.
97 of these are internal, where 97 is the number value of
Haniel, the Archangel of Netzach. The five disjoint 24-cells in the 600-cell have (1 +
5×216 = 1081) corners, where 1081 is the
number value of Tiphareth ("Beauty"). Including its centre, there are 1081 yods
other than vertices in either half of the 24-cell with Type A triangles as its faces.
-
When the faces are Type B triangles, they have 384 corners that are not vertices, 192 in each half. The
number 384 and its 192:192 division are characteristic of sacred geometries (see
The holistic pattern). There are 385 corners
inside the 24-cell, where 385 = 1
2 + 2
2 + 3
2 +
4
2 + 5
2 + 6
2 + 7
2 +
8
2 + 9
2 + 10
2. There are 3360 hexagonal yods in the 96
Type B faces. This means that the 600-cell contains (5×3360=16800) hexagonal yods when its five
24-cells have Type B triangles as their 480 faces. The compound of two 600-cells that is the
4-dimensional projection of the 4
21 polytope defining E
8 has 10
24-cells with 33600 hexagonal yods in their 960 faces.
This is the amazing
way in which the superstring structural parameters 3360 and 16800 are embodied in the 24-cell and
600-cell, themselves holistic entities like the whorl and UPA. Their appearance is
so unambiguous that it can leave no doubt that the UPA is, indeed, an
E
8×E
8 heterotic superstring, for its 16800 circularly polarised waves
(the circular 1st-order spirillae in its 10 whorls) can be resolved into 33600 plane wave
components, each pair of perpendicular plane waves differing in phase by 90°. Each hexagonal yod
denotes such a plane wave, confirming our earlier conclusion that the 120 vertices in each 600-cell
denote the 120 E
8 gauge charges spread along either the outer or the inner half of
the UPA. The 1680 turns in each half-revolution of its 10 whorls comprise 3360 plane waves, each
denoted by a hexagonal yod in a 24-cell, the five half-revolutions of the outer half of the UPA
being generated by the five 24-cells in one 600-cell and the five half-revolutions of its inner half
being generated by the five 24-cells in the other concentric 600-cell. In other words, each of the
10 24-cells in the compound of two 600-cells represents a half-revolution of the 10 whorls of the
UPA, its 24 vertices signifying the 24 E
8 gauge charges that are spread along the
length of a half-revolution.
Tabulated below is the number of geometrical elements in the faces and interior of the
24-cell:
|
Face/internal
triangle
|
Faces |
Interior |
Total |
| |
Corners |
Sides |
Triangles |
Total |
Corners |
Sides |
Triangles |
Total |
Corners |
Sides |
Triangles |
Total |
| Triangle |
24 |
96 |
96 |
216 |
1 |
24 |
96 |
1+120=121 |
1+24=25 |
120 |
192 |
1+336=337 |
| Type A triangle |
24+96=120 |
96 + 96×3 = 384 |
96×3=288 |
792 |
1+96=97 |
24 + 96×3 = 312 |
96×3=288 |
1+ 696=697 |
1+216=217 |
696 |
576 |
1+1488=1489 |
| Type B triangle |
24 + 96×4 = 408 |
96 + 96×12 = 1248 |
96×9=864 |
2520 |
1 + 96×4 = 385 |
24 + 96×12 = 1176 |
96×9=864 |
1+2424=2425 |
1+792 |
2424 |
1728 |
1+4944=4945 |
Comments
-
The number 216 of Geburah is the number of corners, sides & triangles in the
96 faces of the 24-cell when its faces are not divided into sectors. The number of internal geometrical
elements surrounding its centre = 120 = 22 + 42 + 62 +
82 = 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 +
21, i.e., the sum of the squares of the first four even integers and the
sum of the first ten odd integers after 1. This is also the total number of sides. The
total number of geometrical elements surrounding the centre = 336 = 42 +
43 + 44 = 22 + 62 +
102 + 142. This is a superstring structural parameter, being the number of
turns in one revolution of a whorl of the UPA, as well as a structural parameter of sacred geometries
discussed many times in this website. It is a highly significant result because it means
that the compound of five 24-cells generating the vertices of a 600-cell has (5×336=1680) geometrical
elements in them surrounding its centre. This corresponds to the 1680 turns
in the five revolutions of a helical whorl of the UPA. The compound of two 600-cells that
is the 4-dimensional projection of the 421 polytope has 3360 geometrical elements
belonging to 10 24-cells that surround their common centre. This corresponds
to the 3360 plane waves making up each whorl. Alternatively, they
correspond to the 3360 turns in one revolution of all 10 whorls. The 480 faces of each set
of five 24-cells comprise (5×216=1080) geometrical elements that surround their common
centre, making a total of 1081 geometrical elements. This is the number of
Tiphareth ("Beauty").
-
The number 384 characterising holistic systems (see
The holistic pattern) is
the number of sides in the 288 sectors of the faces of the 24-cell when they are Type A triangles.
It is also the number of corners & triangles created by turning each face into a Type A
triangle.
216 corners of (576=24
2) triangles surround its centre.
-
The 24-cell with Type B triangles has 384 corners in its faces other than vertices; it has 385 internal
corners, where 385 = 1
2 + 2
2 + 3
2 +
4
2 + 5
2 + 6
2 + 7
2 + 8
2 +
9
2 + 10
2. Amusingly, it has 2424 sides of 1728 triangles with 792 corners
surrounding its centre, where 792 = 33×24 = (1!+2!+3!+4!)×1×2×3×4. Surrounding its centre are 4944
geometrical elements, where 4944 = 24×206. Again, amusingly, 206 is the number of bones in the adult
human skeleton! The 24-cell has 2520 geometrical elements in its faces. This is the number of turns in
either the inner or outer halves of the three major whorls of the UPA: 3×840 = 2520. As 5040 = 7! and
2520 = 5040/2 = 7!/2, where 7! is the number of permutations of seven objects, the number 2520 is the
number of permutations of
seven objects that exclude the remaining 2520 permutations that
are their mirror images. The faces of the 24-cell have (2520−120=2400) geometrical elements other than
vertices & edges, where 2400 = (1
3+2
3+3
3+4
3)×1×2×3×4
=10×240. Compare this property with the fact that 240 geometrical elements surround the centre of the
Sri Yantra (see
here) and with how this parameter is embodied in other holistic
systems (see
here). According to superstring theory, the number 2400
is the number of space-time components of the 240 10-dimensional gauge fields associated with the
240 roots of the exceptional Lie group E
8. The embodiment of the number 240 in the
geometrical composition of the 24-cell (namely, 240 geometrical elements when faces are triangles
and 240×10 geometrical elements other than vertices & edges when faces are Type A) is yet more
evidence of the holistic nature of the 24-cell.
The geometrical and yod compositions of the 24-cell, therefore, reveal that, as the Coxeter
plane projection of the 240 vertices of the 421 polytope, the compound of two 600-cells contains
all the structural parameters of the UPA. It can leave no doubt whatsoever that the
particle that Annie Besant & C.W. Leadbeater claimed to have remote-viewed over a century ago is a state of the
E8×E8 heterotic superstring.
Home


















