Home

 Proof of uniqueness of encoding

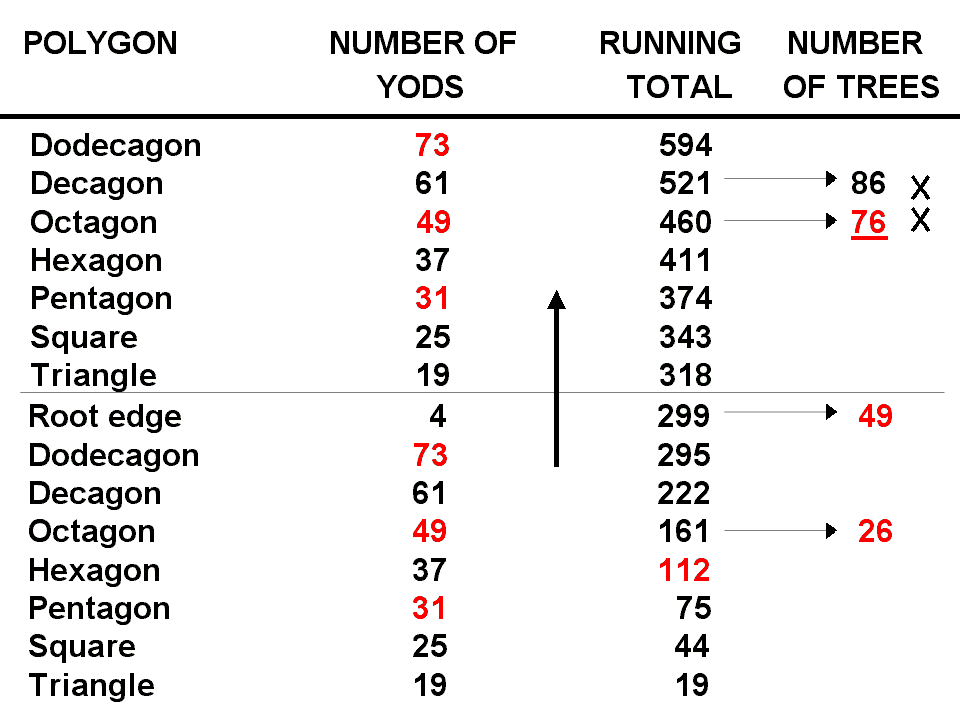
Let us satisfy ourselves that a different (but still sequential) ordering of polygons would not also give rise to an encoding of either CTOL or N overlapping Trees, where N is larger than 91. The table lists the yod populations of the polygons in the inner Tree of Life and their running totals when the second set of seven polygons is reversed, so that they end with the dodecagon instead of the triangle. As before, the first seven polygons and the root edge have the same number of yods as the 49-tree has SLs. The first 12 polygons up the octagon now correspond to 76 overlapping Trees. This is uninteresting (hence the cross against this number) because 76 is smaller than 91, so it has no meaning in the wider context of CTOL. The first 13 polygons correspond to the 86-tree. This is permissible, being less than 91, but uninteresting because it is not 86 overlapping Trees. There is, therefore, no combination of polygons that is the counterpart of N overlapping Trees, where N>91. It is straightforward to confirm (see p. 394 in the author's new book) that neither of the two remaining possible orderings of polygons:

dodecagon-triangle-triangle-dodecagon
dodecagon-triangle-dodecagon-triangle

are satisfactory, the first case because it generates the same results as before, the second case because, whilst it leads to 91 overlapping Trees, a subset of sequential polygons is also equivalent to 36 overlapping Trees, which makes no sense in the context of CTOL with 91 overlapping Trees. Only one ordering of polygons leads to a meaningful set of 91 overlapping Trees. We conclude that the encoding of CTOL in the inner Tree of Life is unique, as one would expect.

For those mathematically inclined, the following analysis provides a rigorous proof of the uniqueness of the 12 polygons as the subset of the 14 polygons with the largest number of yods that conform to the form of the formula N(n) = 6n + 4 for the number (N(n)) of SLs in n overlapping Trees of Life:

the formula

N(C) = 6C + 1

for the N yods in a single polygon with C corners will break down when several, separate polygons with a total of n corners are considered. Consider m such polygons (m>1). They have (6n+m) yods. For what value of n does their yod population conform to this formula, i.e.,

6n + m = N(T) = 6T + 1,

where T is some positive integer denoting a number of overlapping Trees of Life? As n & m are positive integers and

T = n + (m−1)/6,

therefore

m − 1 = 6p,

where p = 1, 2, 3, etc. This means that m = 6p + 1 = 7, 13, etc. The first case when the formula applies to several polygons (m>1) is for seven polygons. This situation applies to the inner form of the Tree of Life, which consists of two sets of seven regular polygons with 48 corners. Here, n = 48 when m = 7, so that T = 48 + 1 = 49. In other words, the yod population of the seven polygons is the same as the number of SLs up to the highest Chesed of 49 overlapping Trees of Life. The meaning of this will become apparent shortly. For the moment, let us extend the analysis into the other half of the inner Tree of Life. Notice that there are four SLs beyond Chesed of the 49th Tree of Life up to its top when that Tree is part of a larger set of overlapping Trees of Life. We might identify them with the four yods on one side of a polygon that belongs to the second set of polygons. If, however, we prefer to identify all of the 49-tree with just one half of the inner Tree of Life because the choice is more natural, then we must let the four yods in the root edge joining the two halves play this natural role in completing the 49-tree by their symbolising the extra four SLs. If m′ polygons in the second set of seven polygons have n′ corners and a yod population that, added to the 299 SLs in the separate root edge and the first set of seven polygons, is equal to the SL population of T′ overlapping Trees of Life (T′>49), then:

6n′ + m′ + 299 = 6T′ + 4

and

T′ = n′ + (m′+295)/6.

As T′ & n′ are positive integers, (m′+295) must be an integer multiple of 6. But 1≤m′≤7. The only value of m′ that satisfies this condition is m′ = 5, so that T′ = n′ + 50. The five types of polygons in the inner Tree of Life with the largest* number of corners are the pentagon, hexagon, octagon, decagon & dodecagon, for which n′ = 41. Therefore, T′ = 91. The SL population of 91 overlapping Trees of Life is 550. This is the yod population of the (m+m′= 7+5=12) regular polygons separated by the root edge with four yods. The five polygons have (6×41 + 5 = 251) yods that correspond to the 251 SLs in the 42 Trees above the 49-tree: 251 + 299 = 550.

Visitors to this website who are Theosophists should realise that this rigorous proof of the encoding of CTOL in a unique subset of the set of 14 regular polygons, which the author claims is the inner form of the Tree of Life, is tantamount to a mathematical proof of the Theosophical doctrine of the seven planes of consciousness, each divided into seven subplanes. The proof given above that the seven polygons making up one half of the inner Tree of Life are equivalent to the Tree of Life mapping of the 49 subplanes of the cosmic physical plane is remarkable evidence supporting this teaching. Its generation of the numbers 91, 299 & 550 as parameters of CTOL renders implausible any suggestion that all these quantitative parallels could arise by chance. The two halves of the inner Tree of Life express the distinction between the words "physical" and "superphysical" — not in their normal sense, in which the former refers to the physical universe and the latter denotes non-material realms of existence, but in a much more general, metaphysical sense that will be familiar only to students of mysticism. The proof confirms the elaboration of the teaching by Alice Bailey and others that the seven planes of consciousness discussed in the early Theosophical literature constitute but the lowest plane of seven planes of cosmic existence. The five polygons with most corners in the second half of the inner Tree of Life encode the Tree of Life/tetractys map of the six superphysical cosmic planes. The nature of these planes can be understood only in a faint, intuitive sense by means of the well-known, hermetic principle of correspondence: "As above, so below," although Bailey's writings may help to provide some insight.

* That the subset of five polygons chosen from the set of seven polygons must have the maxumum number of corners is required because, ex hypothesi, CTOL must consist of the largest number of overlapping Trees, being a map of the Cosmic Whole, not just some section of it.

<< Previous    1...   4  5  [6]  7  8  ...15    Next >>

Home