
| << Previous 1... 11 12 13 14 [15] Next >> |
The 7-pointed star embodies the number of SLs up to Chesed of the 49th Tree of Life
 |
295 = |  |
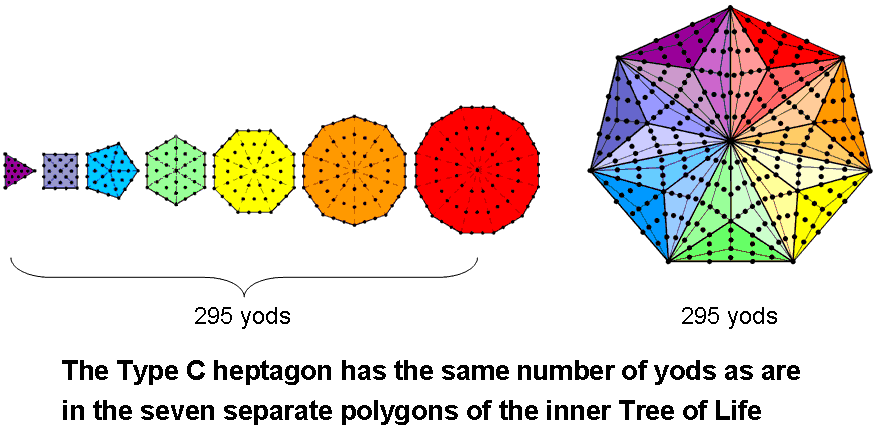
The seven regular polygons making up the inner form of the Tree of Life have 295 yods. Each yod symbolises an SL in CTOL up to Chesed of the 49th Tree of Life. As the first Sephirah of Construction of the uppermost Tree in this section of CTOL that corresponds formally to this Sephirah, this SL marks the formative commencement of the 49 Trees mapping the 49 subplanes of the cosmic physical plane. The seven separate Type A polygons forming one half of the inner form of the Tree of Life map the cosmic physical plane, whilst the five largest of the seven Type A polygons in its other half map the six superphysical cosmic planes.
The number of yods in an nth-order m-gon = 1 + m(3+3n+1)/2, where "1" denotes the yod at its centre (for proof, see the section entitled "The geometrical & yod compositions of polygons" in the General view section of Power of the polygons). The Type C m-gon is the 3rd-order m-gon. It has (42m+1) yods. TheType C heptagon (m=7) has 295 yods. Each of its seven sectors corresponds to one of the seven planes of consciousness, the 42 yods per sector symbolising the 42 SLs in every seven Trees of Life that map the seven subplanes of each plane. The central yod denotes the nadir of CTOL.
A seven-pointed star can be regarded as made up of 14 triangles, seven of which constitute the sectors of a heptagon and seven of which are its points. Next, consider every triangle as a triangular array of dots. When seven dots are equally spaced along each side of an array, the star (including its centre) contains 295 dots. They symbolise the 295 SLs up to Chesed of the 49th Tree, the white central dot denoting the nadir of CTOL. Only three types of star have this property, for an N-pointed star with n dots along each side of its 2N triangles has Nn(n-1)* dots surrounding its centre, so that Nn(n-1) = 294 = 7×7×6 = 49×3×2 = 147×2×1, i.e., either:
1. N = 7 = n,
2. N = 49, n = 3, for which each point corresponds to a subplane, or
3. N = 147, n = 2 (trivial case),
Including its centre, the heptagon with triangular arrays of eight dots as its sectors contains 148 dots, where 148 is the number value of Netzach, the seventh Sephirah from the top of the Tree of Life and the fourth Sephirah from its base. The seven planes of consciousness are the expression of the seven Sephiroth of Construction:
|
Sephirah of Construction |
Plane of Consciousness |
Trees of Life (counting |
||
|
7 |
Chesed |
→ |
Adi, or Divine |
43-49 |
|
6 |
Geburah |
→ |
Anupadaka |
36-42 |
|
5 |
Tiphareth |
→ |
Atmic |
29-35 |
|
4 |
Netzach |
→ |
Buddhic |
22-28 |
|
3 |
Hod |
→ |
Mental |
15-21 |
|
2 |
Yesod |
→ |
Astral |
8-14 |
|
1 |
Malkuth |
→ |
Physical |
1-7 |
The seven subplanes of a plane represent the same seven-fold differentiation within each one. Each subplane is mapped by a Tree of Life. This means that the fourth subplane of the fourth plane, i.e., the 25th subplane mapped by the 25th Tree, is the one that embodies most of all the Divine Quality of Netzach. Netzach of this Tree is the SL that most embodies this Sephiroth of Construction. The number (S(N)) of SLs in N overlapping Trees of Life was derived on page 1 of this section:
S(N) = 6N + 4.
As the N-tree (lowest N Trees in any set of Trees) has one more SL than N overlapping Trees, namely, Yesod of the (N+1)th Tree, it has (6N+5) SLs. Therefore, Chokmah of the Nth Tree in the N-tree is the (6N+4)th SL. Netzach of the 25th Tree is Chokmah of the 24th Tree, which is the (6×24 + 4= 148)th SL. But 148 is the gematria number value of Netzach! We see that the number value of this Sephirah is like a coordinate of a point in space; it specifies the position in CTOL of the SL that expresses Netzach most of all, namely, Netzach of the Tree mapping the fourth subplane of the fourth plane. The 148 dots in the heptagon symbolise the 148 SLs up to Netzach of the 25th Tree, which is the half-way point in the sequence of the 49 Trees mapping the seven planes of consciousness. The remaining (295-148=147) dots in the seven points of the star symbolise the 147 SLs beyond this midpoint up to Chesed of the 49th Tree. This is illustrated by the 147-pointed star in the trivial case 3 listed above. Just as the seven star points and the heptagon are the two "halves" of the seven-pointed star, so the number value 148 of Netzach specifies the midway in the set of 49 overlapping Trees of Life that map the cosmic physical plane: 295 = 147 + 1 + 147. The seven-pointed star is the star-like representation of this "Jacob's Ladder." Its seven sets of point & sector map the seven planes of consciousness, the 42 dots per point & sector symbolising the 42 SLs in the seven Trees of Life that map each plane.
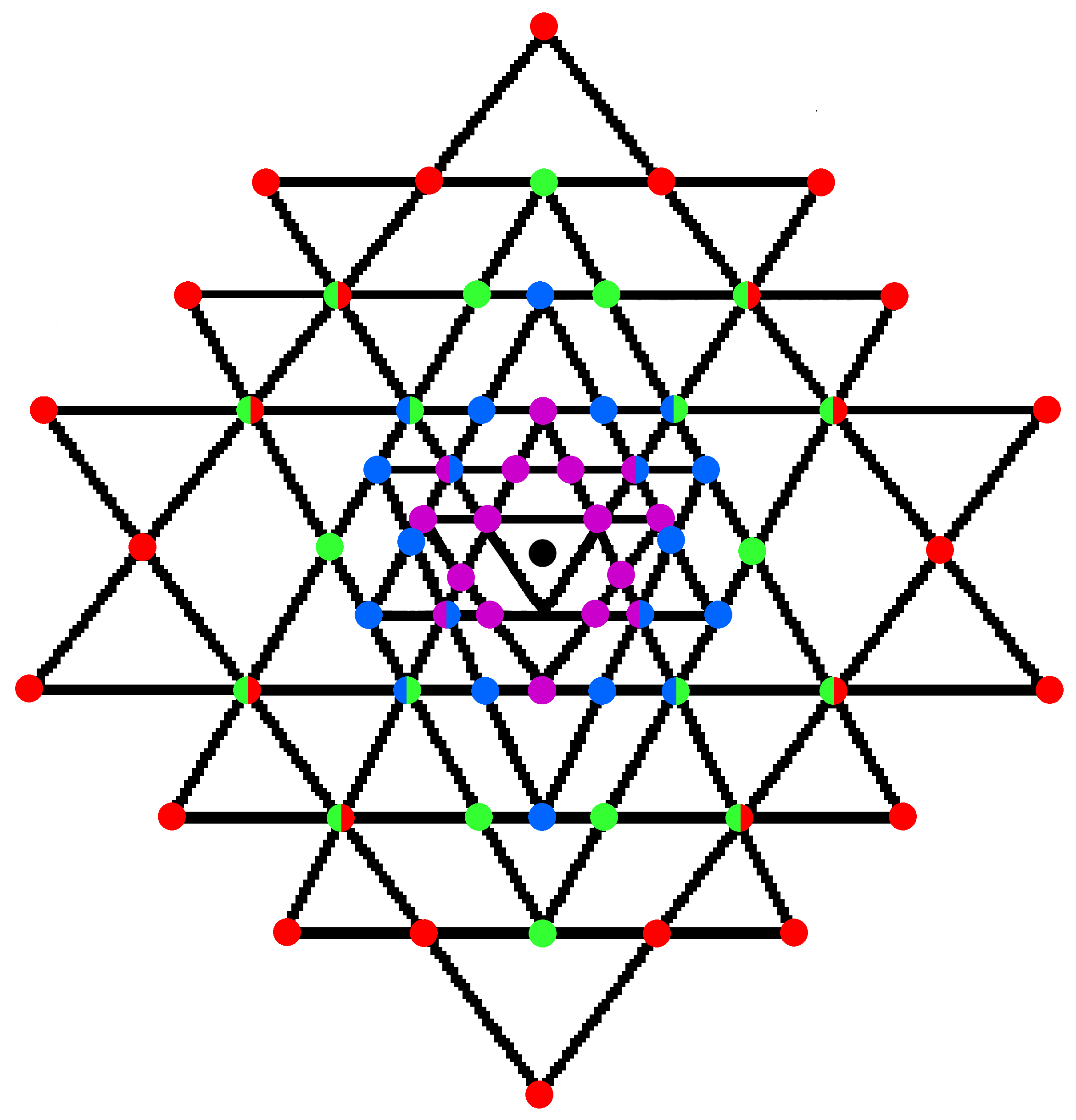
#56 in Wonders of Superstrings discusses how the hexagram (N=6) constructed from triangular arrays of dots with eight dots along each side (n=8) has, using the formula: Number of dots = Nn(n-1) given above, (6×8×7=336) dots surrounding its centre. As discussed widely in other sections, this is the basic structural parameter of the subquark state of E8×E8 heterotic superstrings, being the number of circular turns in each revolution of a helical whorl of the UPA described by Annie Besant & C.W. Leadbeater over 125 years ago in their book Occult Chemistry (see #11 in Occult Chemistry). It is an example of how certain stars such as the pentagram and hexagram — ancient symbols found in the sacred art of ancient religions — embody numbers of cosmic (that is, universal) significance. The reason for this is that some of these stars are isomorphic representations of sacred geometries possessing the same structural parameters that characterise all levels of reality and its most material, elementary forms. Another example is the seven-pointed star (N=7) constructed from 1st-order tetractyses (n=4). It has (7×4×3=84) dots surrounding its centre. This shows its isomorphism with: 1. the 2nd-order tetractys, which has 84 yods surrounding its centre, 2. the inner form of the Tree of Life, whose (7+7) Type B polygons have (84+84) corners of their (141+141) sectors and 3. the 3-d Sri Yantra, whose central triangle is surrounded by the 84 corners of 42 triangles linked in four layers:
|
|
|
|
 |
|
|
|
|
|
In conformity with the Tetrad Principle (see Article 1), which governs the mathematical expression of parameters of holistic systems, the number 84 is the sum of the squares of the first four odd integers:
84 = 12 + 32 + 52 + 72,
and the total number of yods in the 7-pointed star or 2nd-order tetractys, as well as the number of corners of the 141 triangles in the seve enfolded Type B polygons, is 85, where 85 is the sum of the first four powers of 4 (Tetrad):
85 = 40 + 41 + 42 + 43.
Notice that a 7-pointed star has 14 triangles with 15 corners and a 10-pointed star has 20 triangles with 21 corners. This shows how EHYEH, the Godname assigned to Kether with number value 21, and YAH, the older version of YHVH with number value 15, prescribe these two stars. With 1st-order tetractyses as star points and sectors, the N-pointed star has (N×4×3=12N) yods surrounding its centre, so that 120 yods surround the centre of the 10-pointed star. This number is a structural parameter of the inner Tree of Life because — whatever type (i.e., A, B, C, etc) the seven polygons in each half are — 120 yods line their sides:
| 120 = |  |
The 3-pointed star has 36 yods surrounding its centre, so that they symbolise the 36 corners of the seven enfolded Type A polygons. The 7-pointed star has 84 yod surrounding its centre that correspond to the 84 corners associated with each set of seven enfolded Type B polygons The 10-pointed star has 120 yods around its centre that corrrespond to the 120 yods on the sides of the seven enfolded polygons. This shows how the 3-, 7- & 10-pointed stars embody structural parameters of the inner Tree of Life. The 12-pointed star (the tenth type of star) has (12×12=144) yods surrounding its centre. They correspond to the 144 yods inside each half of the inner Tree of Life when composed of seven Type A regular polygons. In general, the number (12N) of yods surrounding the centre of an N-pointed star constructed from tetractyses is the number of yods surrounding the centres of two Type A N-gons, each having 6N such yods. Alternatively, it is the number of yods surrounding the centres of two similar sets of polygons, each with a total of N corners. Hence, a 48-pointed star has the yod population of the (7+7) separate Type A polygons with (48+48) corners that make up the complete inner Tree of Life. This is 12×48 = 576 = 242 = 12×22×32×42, showing how the Pythagorean integers 1, 2, 3 & 4 express this number. Each "half" of this star (i.e., its 48 points or the whole dodecagon) has 288 yods, where
288 = 11 + 22 + 33 + 44.
It corresponds to the seven Type A polygons in each half of the inner Tree of Life, which have (48×6=288) yods surrounding their centres. The number 48 is the gematria number value of Kokab, the Mundane Chakra of Hod.
Below are listed the yod populations (12N+1) of the stars corresponding to the seven types of N-gons present in the inner Tree of Life:
|
N |
3 |
4 |
5 |
6 |
8 |
10 |
12 |
| 12N + 1 | 36 + 1 = 37 | 48 + 1 = 49 | 60 + 1 = 61 | 72 +1 = 73 | 96 + 1 = 97 | 120 + 1 = 121 | 144 + 1 = 145 |
Noteworthy is the ancient symbol of the hexagram (N=6). Surrounding its centre are 72 yods, where 72 is the number value of Chesed. It embodies the number 73 of Chokmah, the Sephirah directly above Chesed on the Pillar of Mercy. This embodiment, as well as that of the structural parameter 336 of the subquark state of E8×E8 heterotic superstrings (as stated above), is discussed here.
The 12-pointed star (dodecagram) (N=12) is the only star for which the number of yods surrounding its centre is the square of the number of its points, for N2 = 12N only if N = 12. The number 12 has special symbolic meaning in the Bible, often depicting completeness. Both the Old and New Testaments find special meaning in the number 12. In the Old Testament, 12 often represents God's people because Israel was comprised of 12 tribes. In the New Testament, 12 may represent the Christian Church, which was built upon the life and ministry of the 12 apostles. Its significance, however, is more important than these historical facts. It has even more cosmic relevance than the ancient astrological meaning of the 12 signs of the zodiac. The number 12 is the number of corners of the tenth polygon and the seventh and largest polygon present in the inner Tree of Life, namely, the dodecagon. As such, this polygon represents completion of the polygonal geometry of the inner form of the Tree of Life. The square of 12 (144) is both the number of yods inside either set of seven enfolded polygons and the number of yods inside them that surround their centres when they are separate. Additionally, it is the number of yods that line the sides of the seven separate polygons, giving them their shapes. Not only does the dodecagon complete the inner Tree of Life but it also — like the seed of a tree — has the potential to generate its outer form, including copies of it in the higher Trees of CTOL. For example, the outer Tree of Life has 16 triangles with 70 yods when they are tetractyses, just as 70 yods surrounding the centre of the dodecagon are associated with either one**. The outer Tree of Life needs 144 (=122) more yods*** to convert them to Type A triangles. The number 12 also determines the oscillatory form of the subquark state of the E8×E8 heterotic superstring, for there are 168 circular turns in each half-revolution of a helical whorl of the UPA, where 168 (the number of Cholem Yesodoth, the Mundane Chakra of Malkuth) is the sum of the first 12 odd integers after 1:
168 = 132 - 1 = 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25.
* Proof: Number of dots in a triangular array of dots with (n-1) dots spaced evenly along each
side = 1 + 2 + 3 +... + n-1 = n(n-1)/2. This is the number of dots other than its centre per triangular array
sector of an N-gon with n dots along each side. Number of dots surrounding the centre of an N-pointed star with
triangular arrays as its star points and sectors of its central N-gon = N[n(n-1)/2 + n(n-1)/2] = Nn(n-1).
** Proof: Of the 73 yods in a Type A dodecagon, two yods on the root edge can be associated
with the other dodecagon. This leaves 71 yods, so that 70 yods surrounding its centre are asociated with each
one.
*** Proof: Inside a Type A triangle are 10 yods — nine more than for a tetractys (see here). Converting the 16 triangles in the outer Tree of Life to Type A triangles
instead of tetractyses requires (16×9=144=122) more yods.
| << Previous 1... 11 12 13 14 [15] Next >> |