| << Previous 1... 2 3 [4] 5 6 ...15 Next >> |

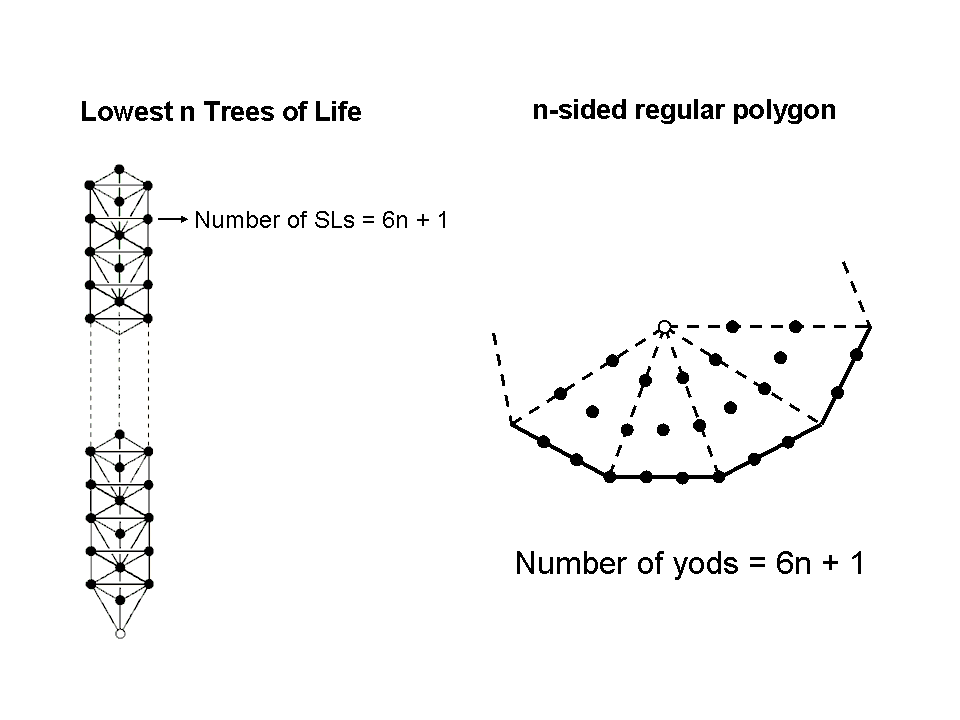
Consider n overlapping Trees of Life. Starting from its lowest SL, six more SLs are present in successive Trees up to Chesed of each one. The number of SLs up to Chesed of the nth Tree = 6n + 1.
Consider an n-sided polygon (it need not be regular). Turn each of its sectors into tetractyses. Six yods are added per sector. Including its centre, which is shared by all n tetractyses, the n-sided polygon is constructed from n tetractyses with (6n+1) yods. This establishes that such a polygon is equivalent to n overlapping Trees of Life up to Chesed — the first Sephirah of Construction — of the nth Tree. Enclose the polygon in a square and it becomes the counterpart of the complete n-tree, the four corners of the square corresponding to Kether, Chokmah, Binah & Daath of the nth Tree of Life. The centre of the polygon corresponds to Malkuth of the first Tree. The 2n hexagonal yods on its sides correspond to the n pairs of Chesed & Geburah of the n Trees and the n corners and n centres of tetractyses correspond to their Yesods & Tiphareths.
| << Previous 1... 2 3 [4] 5 6 ...15 Next >> |