The Tree of Life/1-tree compared with the 1st (6+6) enfolded polygons

Comments

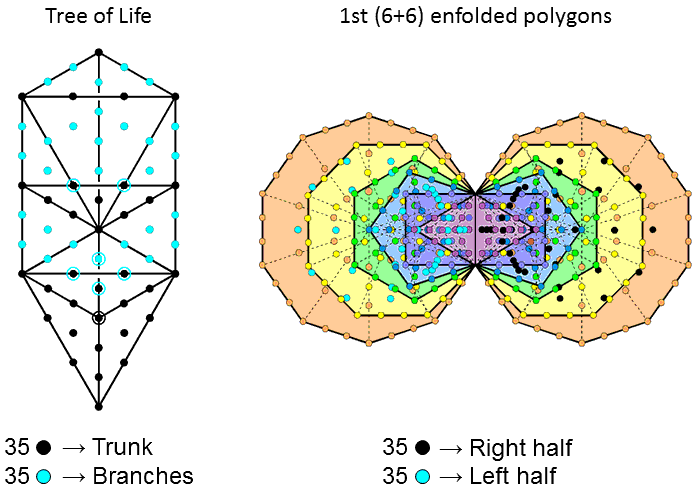
The trunk of the Tree of Life consists of:

• Point (Kether)
• Line (Chokmah-Binah Path)
• Triangle (Chesed-Geburah-Tiphareth)
• Tetrahedron (Netzach-Hod-Yesod-Malkuth)

The rest of the Tree of Life constitutes its branches. When the 16 triangles of the Tree of Life are tetractyses, its trunk contains 35 yods (coloured black), as do its branches containing turquoise yods.

The counterpart in the 1st (6+6) enfolded polygons of this 35:35 division is the 35 black hexagonal yods at the centres of the 35 tetractyses in the right-hand set of 6 polygons and the 35 turquoice hexagonal yods at the centres of the 35 tetractyses in the left-hand set of 6 polygons.

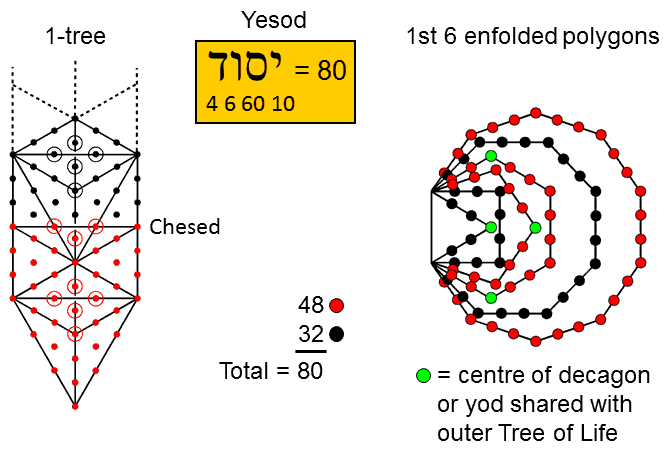
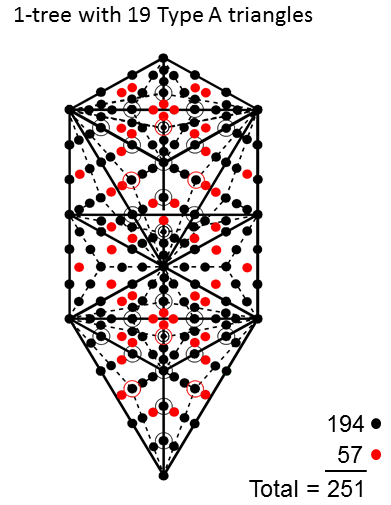
The 1-tree comprises 19 triangles. When they are tetractyses, they contain 80 yods, where 80 is the number value of Yesod, the penultimate Sephirah of the Tree of Life. There are 48 red yods up to Chesed, the first of the 7 Sephiroth of Construction. The remainder of the 1-tree above Chesed has 42 black yods.

Compare this with the yods lining the 31 sides of the 1st 6 enfolded polygons, which have 26 corners, where 26 is the number value of YAHWEH, the Godname of Chokmah, and 31 is the number value of EL, the Godname of Chesed below Chesed on the Pillar of Mercy. The number of yods lining the sides = 26 + 2×31 = 88. Four yods line the root edge, outside which are 84 yods lining the 30 other sides. The top & bottom corners of the hexagon and the right-hand corner of the triangle coincide with corners of triangles belonging to the outer Tree of Life. As well as these 3 shared yods (shown as green), a corner of the pentagon coincides with the centre of the decagon. The number of yods lining sides outside the root edge that surround centres of polygons = 84 − 3 − 1 = 80. of these, 32 black yods line the triangle, square & octagon and 48 red yods line the pentagon, hexagon & decagon.

The numbers of intrinsic yods outside the root edge that surround centres of polygons are:

(first numbers are the numbers of corners; second numbers are numbers of hexagonal yods). 32 yods line the hexagon & octagon. But this is not an alternative counterpart to the 32 yods above Chesed in the 1-tree because they include Kether, Chokmah, Binah & Daath but only the triangle displays a set of 4 yods.

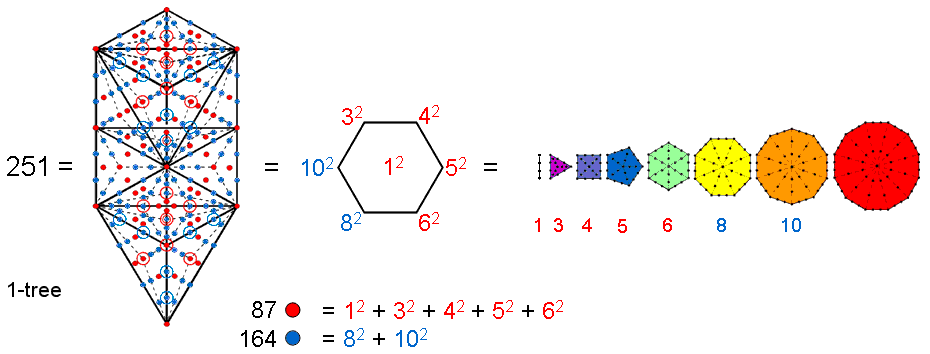
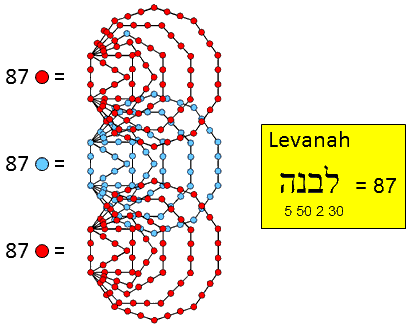
Constructed from Type A triangles, the 1-tree contains 251 yods. They comprise 11 red corners of 19 Type A triangles with 25 sides lined by (25×2=50) blue hexagonal yods. Inside them are 19 red corners, (3×19=57) red hexagonal yods at the centres of their 57 tetractyses, and (6×19=114) blue hexagonal yods on sides of tetractyses. The yod population of 251 divides into a set of 87 red yods and a set of 164 blue yods. 87 is the number value of Levanah, the Mundane Chakra of Yesod.

The number of yods lining the n tetractyses in an n-gon = 5n + 1. The number of yods lining the 48 tetractyses in the 7 separate regular polygons making up half of the inner Tree of Life = ∑(5n+1) = 5×48 + 7 = 247. Including the separate root edge with 4 yods, 251 yods line their sides. This is the number of yods in the 1-tree. The number 251 is determined by the first 6 polygons because the sum of the squares of the numbers of their corners is 250:

250 = 3² + 4² + 5² + 6² + 8² + 10²,

so that, associating one endpoint of the root edge with the 1st 6 polygons and assigning the number 1 to it:

251 = 1² + 3² + 4² + 5² + 6² + 8² + 10².

That this remarkable arithmetic connection between the two geometrical systems cannot be the product of coincidence is indicated by the fact that the number 87 is the sum of the first 5 squares and the number 164 is the sum of the last two squares:

87 = 1² + 3² + 4² + 5² + 6²

164 = 8² + 10².

The 1st 6 enfolded polygons have 26 corners and 31 sides. When they are Type A, (26 + 31×2 = 88) yods line their sides. The top corner of the hexagon coincides with the lowest corner of the hexagon belonging to the inner form of the next higher Tree of Life. 87 yods are intrinsic to the first 6 of the 7 enfolded polygons making up the inner forms of successive Trees. Notice in the diagram opposite that the top corner of the hexagon in the lowest set of polygons is coloured blue, not red, because it is shared with the hexagon with blue yods belonging to the inner form of the next higher Tree. Similarly, the top corner of the middle hexagon is red, not blue, because it is not intrinsic to the middle set of polygons, being shared with the hexagon in the top set of polygons with red yods.

The 87 yods are intrinsic to each set of 6 enfolded polygons and line their sides, shaping them. They comprise 30 yods lining the decagon and 57 yods lining the first 5 polygons. They correspond, respectively, to the 30 corners of the 57 tetractyses in the 1-tree and the 57 hexagonal yods at the centres of the latter.

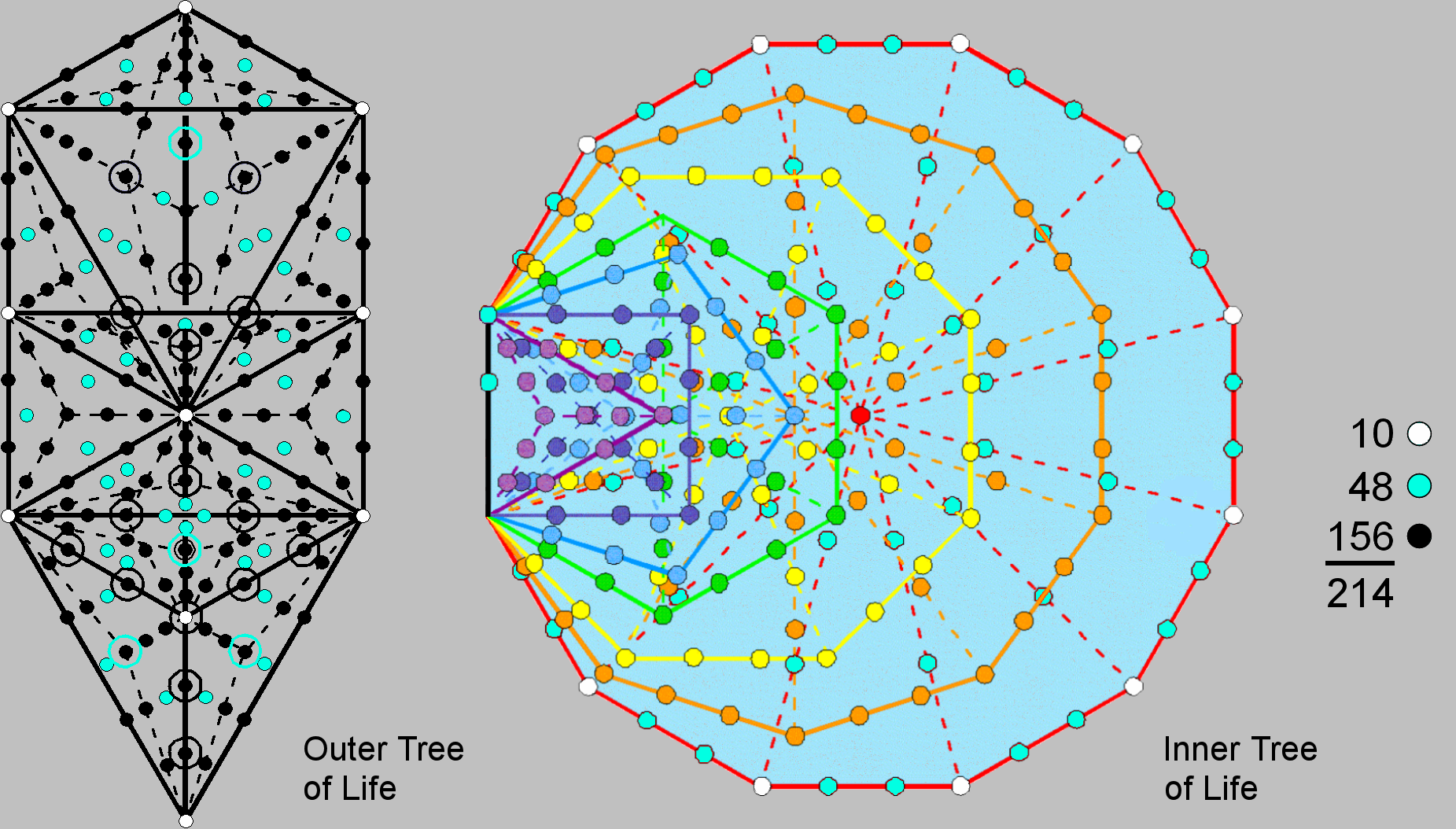
When its 16 triangles are Type A, the Tree of Life contains (16×3=48) turquoice hexagonal yods at the centres of the (16×3=48) tetractyses. Each Type A triangle contains 7 more (black) yods. The 16 triangles have 10 white corners and 22 sides, each with two black hexagonal yods. The number of yods in the Tree of Life = 10 + 22×2 + 16×7 + 48 = 214.

The 7 enfolded polygons have 47 sectors with 41 corners and 88 sides. The number of yods lining the sides of the 47 tetractyses = 41 + 88×2 = 217. The top of the hexagon coincides with the bottom of the hexagon belonging to the inner form of the next higher, overlapping Tree of Life. This means that 216 boundary yods are intrinsic to each set of 7 enfolded polygons, where 216 is the number of Geburah. Two yods on the root edge can be associated with each set of 7 enfolded polygons. Associated with each half of the inner Tree of Life are (216−2=214) intrinsic yods lining 47 tetractyses. This is the number of yods in the Tree of Life with Type A triangles. The 10 white corners of the dodecagon outside the root edge correspond to the 10 white yods located at the Sephiroth. The 48 turquoice yods lining either sides of the sectors of the dodecagon correspond to the 48 hexagonal yods at the centres of the 48 tetractyses in the 16 Type A triangles of the Tree of Life. The 156 remaining yods correspond to the 156 black yods lining the sides of these tetractyses.

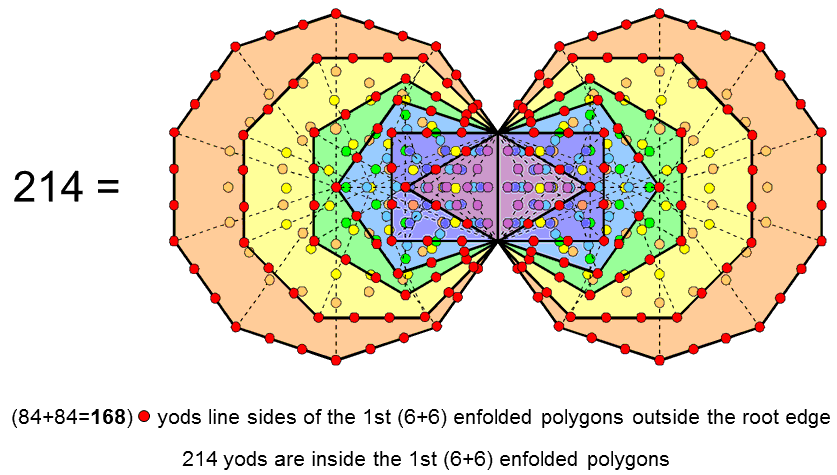
It was shown in the previous comment that the number 214 is a parameter of both the outer and inner forms of the Tree of Life. It will now be shown that it re-appears as a parameter of the 1st (6+6) enfolded polygons.

The (7+7) enfolded Type A polygons have 524 yods. The Type dodecagon has 73 yods (69 outside the root edge it shared with the other polygons of the inner Tree of Life). The number of yods in the 1st (6+6) enfolded polygons = 524 − 2×69 = 386 (382 outside the root edge). The 1st 6 enfolded polygons have 24 corners and 30 sides outside the root edge that are lined by (24 + 30×2 = 84) yods. The number of red yods lining the 60 sides of the 1st (6+6) enfolded polygons outside the root edge = 2×84 = 168. This is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth. Inside these polygons are (382−168=214) yods. There are as many yods inside them as there are yods needed to construct the outer Tree of Life from Type A triangles. The 70 hexagonal yods at the centres of the 70 tetractyses in the 1st (6+6) enfolded polygons are the yods needed to construct the outer Tree of Life from tetractyses, the extra 144 yods lining internal sides of these tetractyses being the extra 144 yods needed to transform the 16 triangles from tetractyses into Type A triangles.

The property of 168 yods outside the root edge lining the 1st (6+6) enfolded polygons has great significance vis-à-vis the identification by the author of the basic unit of matter by Annie Besant & C.W. Leadbeater (see here) in terms of the subquark state of E₈×E₈ heterotic superstrings. It is discussed further on #48 of Superstrings as sacred geometry/Tree of Life.

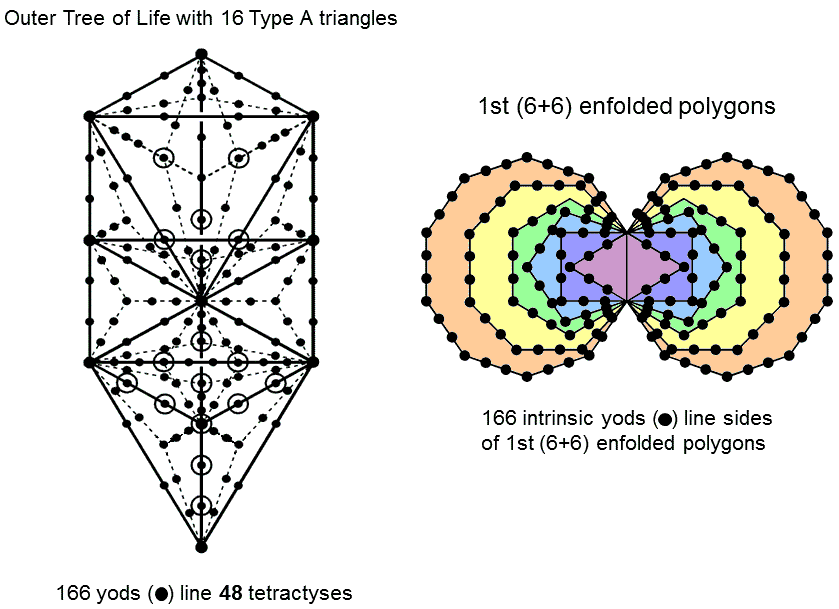
The Tree of Life with 16 Type A triangles contains 214 yods. Of these, (3×16=48) hexagonal yods are at the centres of the 48 tetractyses in these triangles. The number of yods lining tetractyses = 214 − 48 = 166.

It was shown in the previous comment that 168 yods outside the root edge line the sides of the 1st (6+6) enfolded polygons. The topmost corners of their two hexagons are the bottom corners of the two hexagons belonging to the inner form of the next higher, overlapping Tree of Life. 166 boundary yods outside the root edge are therefore intrinsic to each set of the 1st (6+6) enfolded polygons.

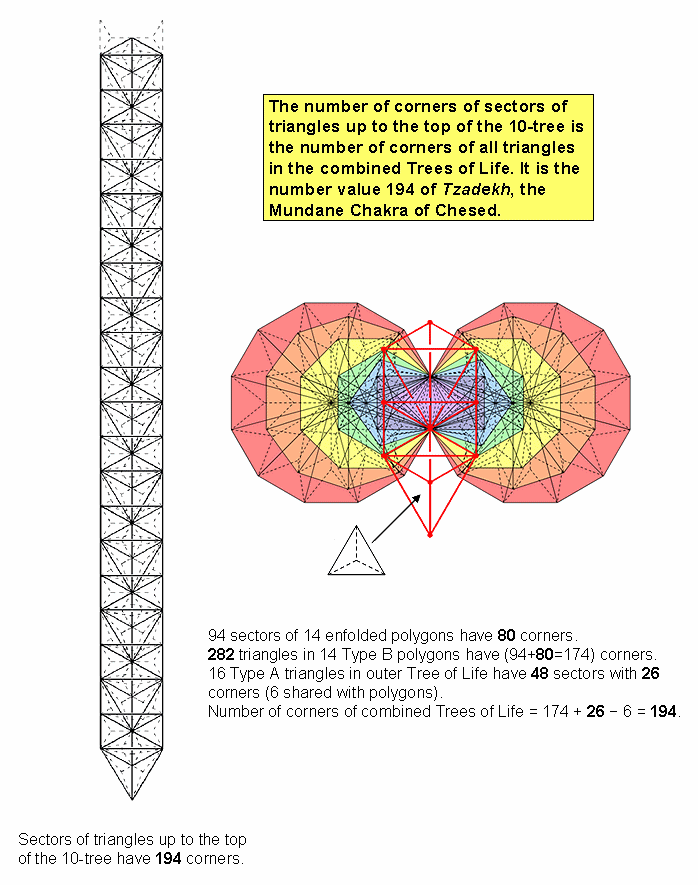
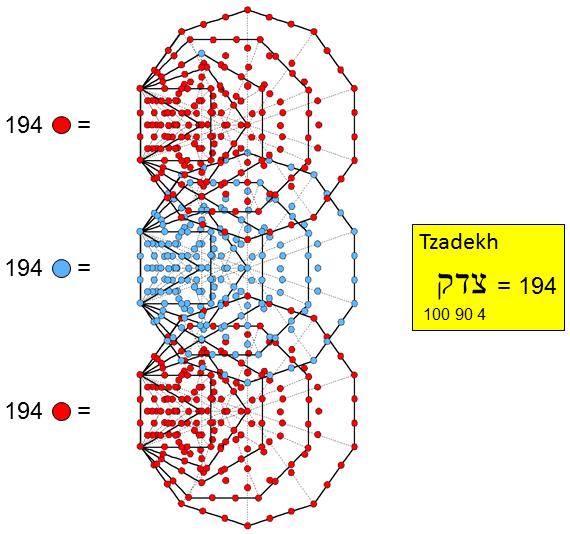
The (12n+7) triangles in the n-tree have (6n+5) corners. When they are Type A, the number of corners of their (36n+21) sectors = 12n + 7 + 6n + 5 = 18n + 12. The 381 sectors of the 127 Type A triangles in the 10-tree have 192 corners. There is one corner of a sector on either side of the top of the 10-tree at the same level. Therefore, there are (192+2=194) corners of sectors up to the top of the 10th Tree of Life. This is the number value of Tzadekh, the Mundane Chakra of Chesed.

Consider the combined outer & inner Trees of Life with Type A triangles in the former and Type B polygons in the latter. The number of corners of the (16×3=48) sectors of the 16 Type A triangles = 10 + 16 = 26. Of these, 3 corners coincide with the top, centre & bottom of the hexagon in the right-hand set of 7 Type B polygons and 3 corners coincide with the top, centre & bottom of the hexagon in the left-hand set of 7 polygons. The (7+7) enfolded polygons have 94 sectors with 80 corners. Each sector is a Type A triangle, so that the number of corners of the (3×94=282) sectors = 80 + 94 = 174. Six of these corners are shared with the outer Tree of Life. The number of corners of the (48+282=330) sectors of the triangles in the combined outer & inner Trees of Life = 26 + 174 − 6 = 194. This is the number of corners of the sectors of triangles up to the top of the 10-tree.

The 1-tree has 19 triangles with 11 corners and 25 sides. When they are Type A, each triangle has 10 yods inside it. The number of yods in the 1-tree = 11 + 25×2 + 19×10 = 251. A red hexagonal yod is at the centre of the (19×3=57) sectors of the triangles. The number of yods lining the (25 + 3×19 = 82) sides of the 57 tetractyses = 251 − 57 = 194. This is also the number of corners of sectors in the triangles making up the combined Trees of Life.

The 7 enfolded Type A polygons in each half of the inner Tree of Life have 264 yods (see here). The Type A dodecagon has 73 yods (69 outside the root edge). The number of yods in the 1st 6 enfolded polygons = 264 − 69 = 195. The topmost corner of the hexagon in this set is the only corner that is shared with polygons belonging to the inner form of the next higher Tree of Life because it coincides with the bottom corner of the hexagon in this adjacent set of polygons. 194 yods are unshared and intrinsic to each set of polygons making up the inner form of successive Trees of Life. Notice in the diagram above that the top of the hexagon in the lowest set of polygons is blue, not red, because it is shared with the next higher set of polygons containing blue yods. Similarly, the top of the hexagon in the middle set of polygons is red, not blue, because it coincides with the bottom corner of the hexagon in the top set of polygons.

The number value of Tzadekh, the Mundane Chakra of Chesed, appears as a parameter of the 10-tree, the combined Trees of Life, the 1-tree and the 1st 6 enfolded polygons because these are all holistic systems mathematically characterised by the gematria number values of the 10 Sephiroth in the 4 Worlds of Atziluth (Godnames), Beriah (Archangels), Yetzirah (Orders of Angels) & Assiyah (Mundane Chakras).

Although not indicating correspondence between the 1st 6 enfolded polygons and the outer Tree of Life or 1-tree, the property of the former discussed below demonstrates how naturally the system of numbers associated with the 10 Sephiroth quantify sacred geometries.

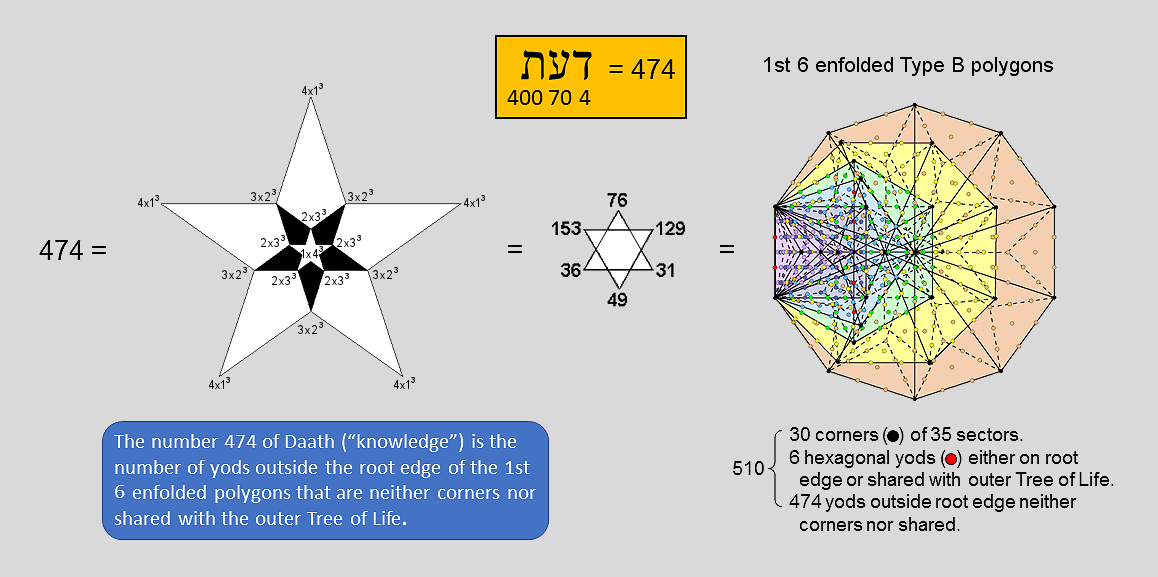
Daath is the ontological gulf separating objective levels of existence expressed by the 7 Sephiroth of Construction from the subjective level of the Divine Life within the triple Godhead of Kether, Chokmah & Binah. It literally means "knowledge". This is not second-hand information of the kind read in books about which the reader has no proof or even experience. It is direct, experiential knowledge. Its gematria number value is 474. Given that the Tree of Life is equivalent to the Pythagorean tetractys symbolising the integers 1, 2, 3 & 4, which express its geometrical and yod composition, it should not come as a surprise that the number 474 can be represented by a 5-fold array of numbers of the form n(5−n)³, where n = 1, 2, 3 & 4. The number 1×4³ is assigned to the centre of a 5-pointed star, the number 2×3³ is assigned to its points, the number 3×2³ is assigned to the points of a 5-pointed star enclosing the first one and the number 4×1³ is assigned to the points of a third 5-pointed star enclosing the second one.

The number value 474 of Daath is the sum of the Godname numbers of the first 6 Sephiroth of Construction:

474 = 31 (EL) + 36 (ELOHA) + 76 (YAHWEH ELOHIM) + 129 (YAHWEH SABAOTH) + 153 (ELOHIM SABAOTH) + 49 (EL CHAI).

The inner form of the Tree of Life with Type B polygons contains 1370 yods (see here). Each half of it has 687 yods. The Type B dodecagon has 181 yods (177 yods outside the root edge). The number of yods in the 1st 6 enfolded Type B polygons = 687 − 177 = 510. They comprise the 30 corners of the 35 sectors of the 1st 6 enfolded polygons, two red hexagonal yods on the root edge, 4 red hexagonal yods on the two vertical sides of sectors inside the hexagon, which are shared with the outer Tree of Life, and 474 yods outside the root edge which are neither corners of sectors nor shared. Transformation of the 1st 6 enfolded polygons into Type B polygons generates or requires 474 more yods outside the root edge that are intrinsic to them. This demonstrates how naturally the 1st 6 enfolded polygons embody the number 474 of Daath. Knowing this fact by having personally proved it is an example of what constitutes "knowledge" of the Tree of Life.