The holistic nature of the first (6+6) enfolded polygons

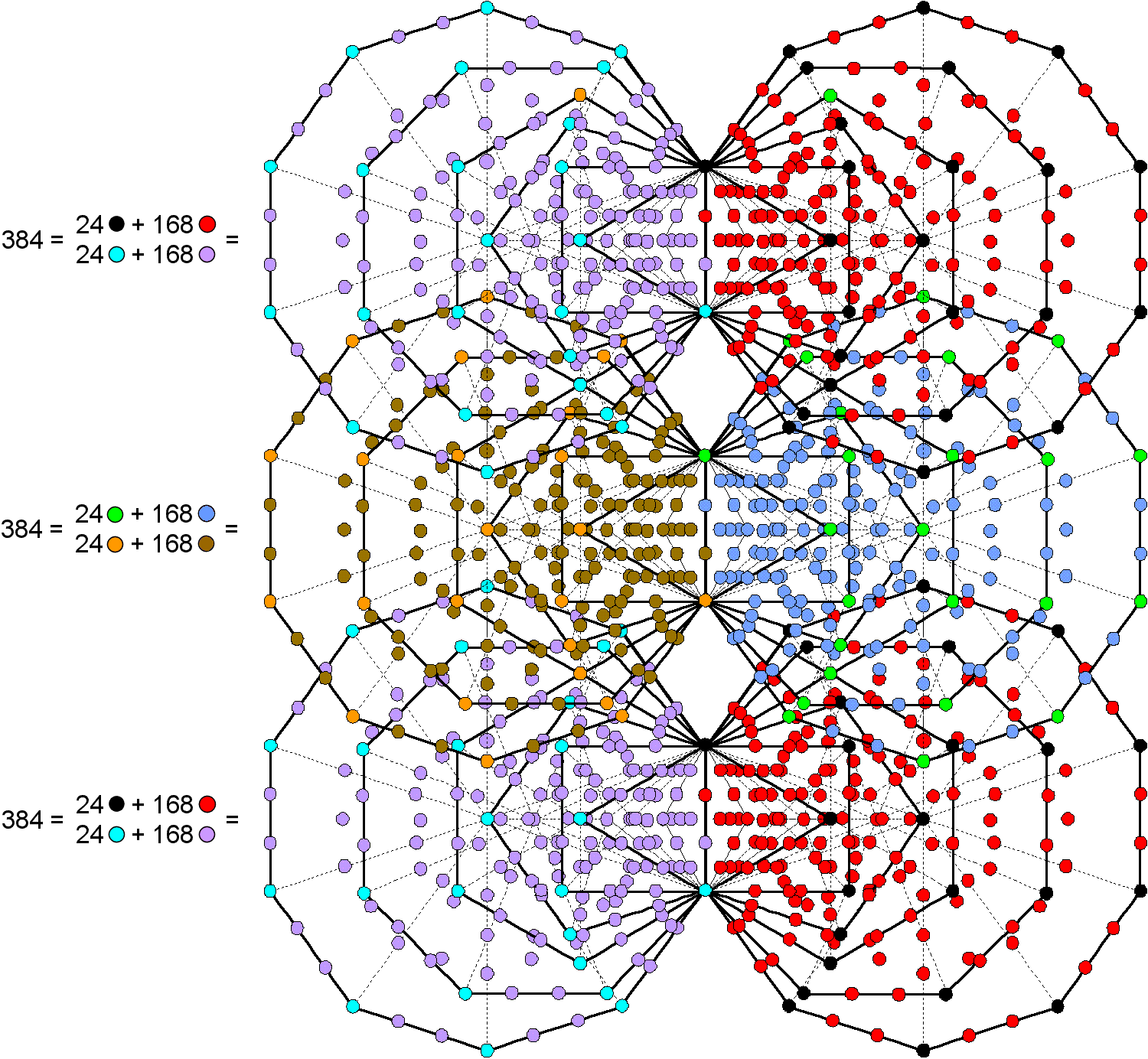
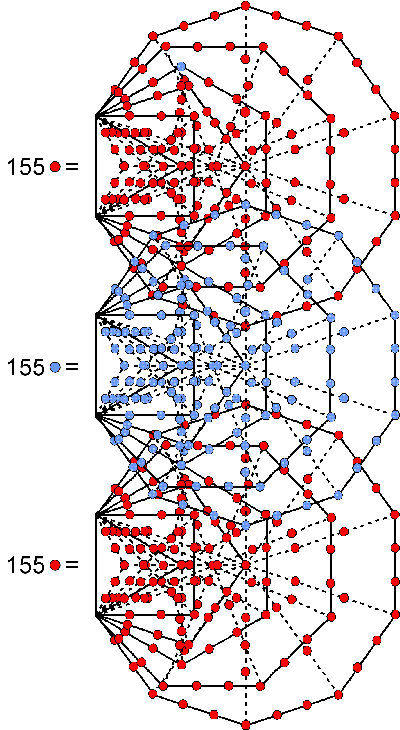
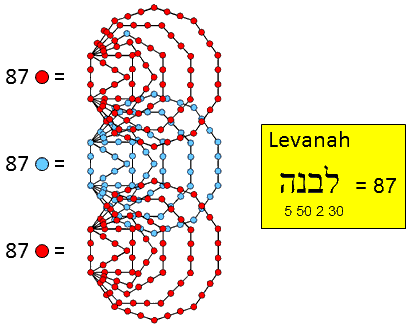
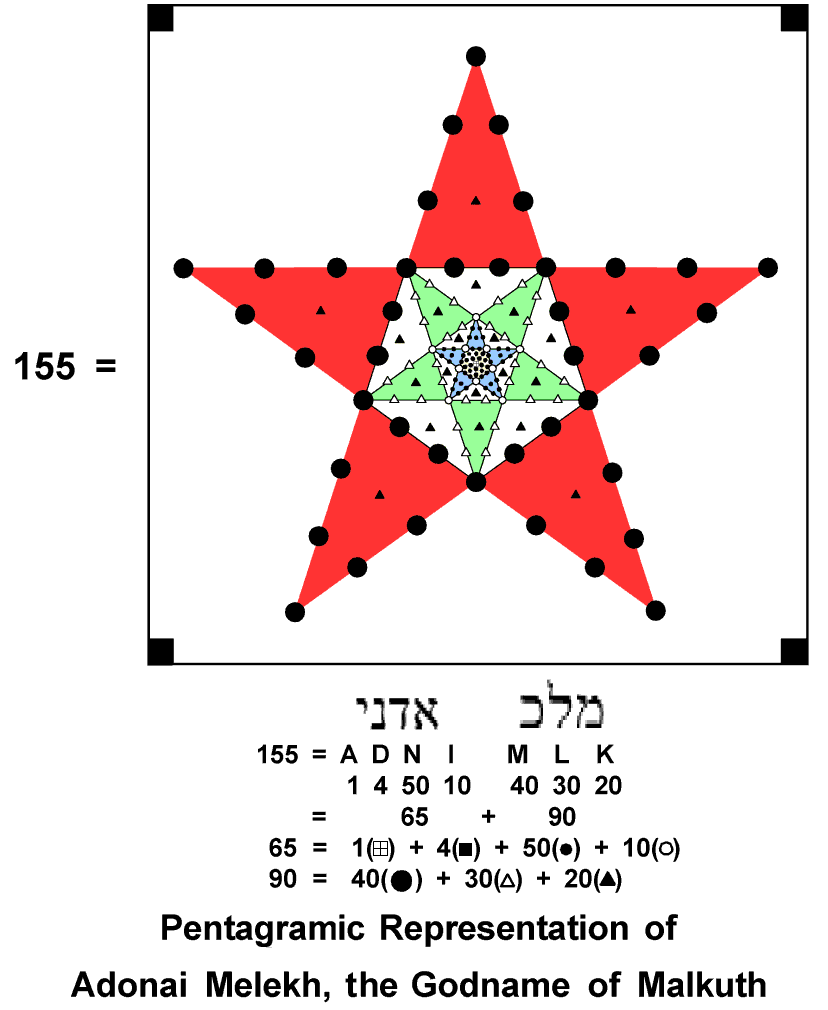
The 1st (6+6) Type A polygons enfolded in every overlapping Tree of Life have 384 intrinsic yods. Each set of 6 enfolded polygons has 24 intrinsic corners and 168 yods. This 24:168 pattern characterises holistic systems/sacred geometries. 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth.	Outside the root edge of the 14 polygons enfolded in the inner form of successive, overlapping Trees of Life are 155 yods lining the sides of the 35 tetractyses in each set of the 1st 6 polygons. 155 is the number value of ADONAI MELEKH, the complete Godname of Malkuth.	The number 87 of Levanah, the Mundane Chakra of Yesod, is the number of yods intrinsic to, and lining, the sides of the 1st 6 polygons enfolded in the inner form of successive, overlapping Trees of Life.

 We saw earlier that the Godnames of the 10 Sephiroth mathematically prescribe the 1st 6 enfolded polygons of the inner Tree of Life. This means that this subset of the complete set of 7 enfolded polygons constitutes a holistic system in itself. As conclusive evidence of this, consider the following:

• the (7+7) enfolded Type A polygons contain 524 yods. The dodecagon has 69 yods outside the root edge. The number of yods in the 1st (6+6) enfolded polygons = 524 − 69 − 69 = 386. The topmost corners of the two hexagons coincide with the the lowest corners of the two hexagons belonging to the inner form of the next higher Tree of Life. Therefore, 384 yods are intrinsic to the 1st (6+6) polygons making up the inner form of each Tree, each set of 6 polygons having 192 intrinsic yods associated with it. The 12 enfolded polygons have 50 corners, where 50 is the number value of ELOHIM (אלהים), the Godname of Binah. (50−2=48) corners are intrinsic to each set of 12 polygons enfolded in successive inner forms of overlapping Trees of Life. There are (384−48=336) yods that are not corners (168 associated with each set of 6 polygons). Hence, successive sets of the 1st (6+6) polygons display the divisions:

384 = 192 + 192

192 = 24 + 168

that are characteristic of holistic systems (see The holistic pattern).

• As there are 386 yods in both sets of the 1st 6 enfolded polygons, each set has (193+2=195) yods. As one yod is shared with the polygons enfolded in the next higher Tree of Life, 194 yods are intrinsic to each set, where 194 is the number value of Tzadekh, the Mundane Chakra of Chesed. Of these, 35 are hexagonal yods at centres of their 35 tetractys sectors. (194−35=159) yods line their sides. Of these, 155 lie outside the root edge with 4 yods. This shows that ADONAI MELEKH, the Godname of Malkuth with number value 155, prescribes the first 6 enfolded polygons by shaping their form. If the corner of the triangle that coincides with the centre of the hexagon is counted as belonging to the latter, the triangle, square & octagon have 65 boundary yods, where 65 is the number value of ADONAI, and the pentagon, hexagon & decagon have 90 boundary yods, where 90 is the number value of MELEKH (this is the only combination of polygons that generates both numbers). Constructed from tetractyses, a pentagram enclosed in a square naturally represents the number values of both ADONAI and MELEKH, the numbers of their individual letters denoting the numbers of yods belonging to a certain class:

The 35 sectors in the 1st 6 enfolded polygons have 65 sides, showing how ADONAI with number value 65 prescribes their form.

• The 1st 6 enfolded polygons have 26 corners and 31 sides, showing how YAHWEH, the Godname of Chokmah with number value 26, and EL, the Godname of Chesed with number value 31, prescribe these enfolded polygons. The number of yods lining their sides = 26 + 2×31 = 88. One of them is shared with the polygons enfolded in the next higher Tree. Therefore, 87 yods that are intrinsic to each set of 6 enfolded polygons line their sides and give shape to them. The number 87 is the number value of Levanah, the Mundane Chakra of Yesod.

Comparing these result with the finding discussed in the previous page, we notice that 168 yods outside the root edge line the sides of the 1st (6+6) enfolded polygons, whilst 168 yods other than corners are associated with each set of 6 enfolded polygons. Here are two amazing ways in which they embody the superstring structural parameter 168. Anyone who wants to believe that both properties could be due to chance has to believe in miracles as well!

Superstring meaning of the 24:168 division of yods
Listed below are the numbers of roots in the five exceptional groups and the numbers of types of roots in E₈, the largest one:

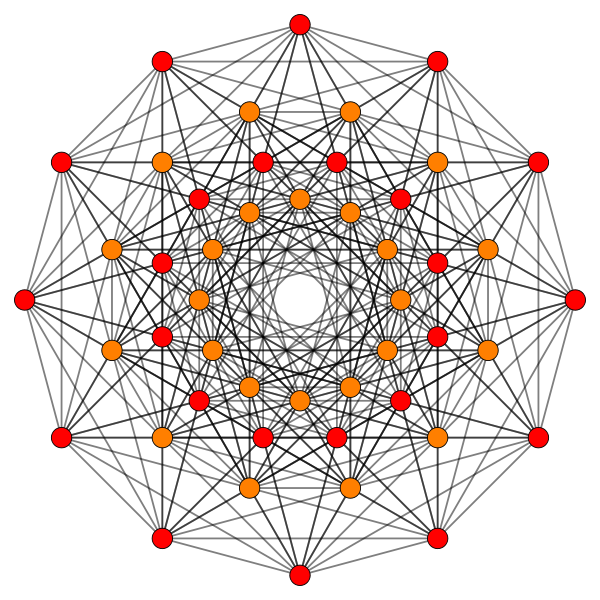
E₈, the largest exceptional group, has 168 more roots than the rank-6 E₆, one of its subgroups. E₆ has 24 more roots that its exceptional subgroup F₄. The group E₈ has therefore (24+168=192) more roots than F₄. They are denoted by the 192 intrinsic yods of the 1st 6 polygons enfolded in successive Trees of Life. The 24 intrinsic corners denote the 24 roots in E₆ that do not belong to F₄ and the 168 yods denote the 168 roots in E₈ that do not belong to E₆. The 384 intrinsic yods in each set of (6+6) enfolded polygons reflects the fact that each half of an inner Tree of Life embodies the group E₈, implying that the symmetry group consistent with the geometry of the inner Tree of Life is E₈×E₈. For examples of how other sacred geometries embody the holistic patterns 24:192 and 48:336, see #19 & #36 in Wonders of correspondences. As the inner form of the Tree of Life, too, conforms to these patterns (see the first link just given), the 48 roots of F₄ must also exhibit them. Indeed, they do! The 240 roots of rank-8 E₈ are represented by 240 8-dimensional position vectors, all with length √2. They have (240×8=1920=192×10) coordinates, so that (3840=384×10) coordinates define the (240+240=480) roots of E₈×E₈. The holistic parameter 384 re-appears in the F₄ groups in E₈×E₈ as the (48×8=384) coordinates of either one. It is known that the 48 roots of F₄ are the 48 vertices of a 24-cell in two dual configurations:

24-cell vertices
24 roots at (±1,±1,0,0), permuting coordinate positions.

Dual 24-cell vertices
8 roots at (±1, 0, 0, 0), permuting coordinate positions.
16 roots at (±½, ±½, ±½, ±½).

(see here). They are shown below:

Coxeter plane projection of the 48 root vectors of F4, represented by the 24 red vertices of a 24-cell and the 24 orange vertices of its dual.	The 24-cell.

The 24-cell has 96 edges and 96 triangular faces, i.e., 192 edges & faces, so that the two 24-cells with 48 vertices defining the 48 roots of F₄ have (192+192=384) edges & faces. The holistic parameters 192 and 384 appear not only in the 192 roots of E₈ and the 384 roots of E₈×E₈ not belonging to their F₄ groups but also in the very geometry of the representation of the roots of F₄! It is implausible that this could be due to coincidence. Instead, it implies that F₄ (which contains as a subgroup G₂, the automorphism group of the octonion algebra) is itself a holistic object, just as E₈ and E₈×E₈ are.

 

<< Previous    1...   46  47  48  [49]  50    Next >>

Home