| << Previous 1... 45 46 [47] 48 49 ...50 Next >> |
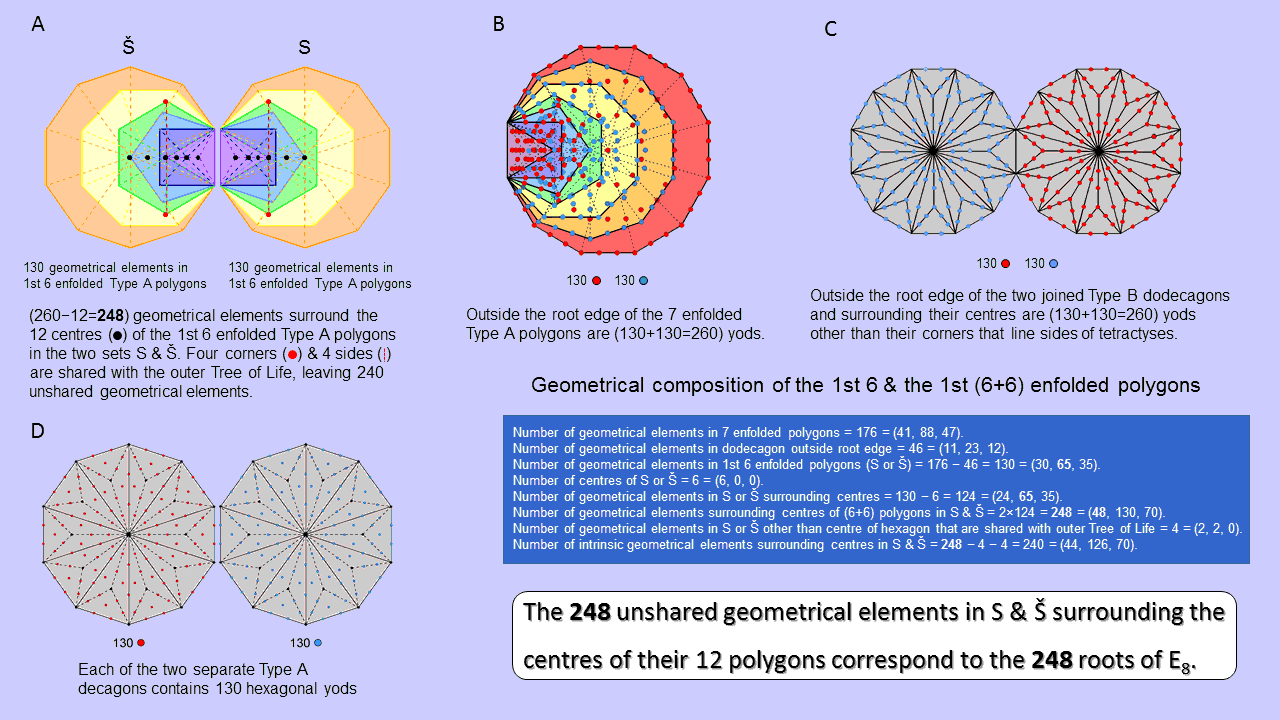
The two separate sets of the first 6 enfolded Type A polygons embody the dimension 248 of E8

We discussed in comment 9 on page 42 examples of how the Godname YAHWEH with number value 26 prescribes various holistic systems by dividing them into two "halves", each with 13 members. This division is also exhibited in subsets of these systems that are holistic in themselves because they, too, are prescribed by the Godnames of the 10 Sephiroth. For example, Article 4 showed that the first 6 of the 7 enfolded polygons making up half of the inner form of the Tree of Life constitute a holistic system characterised by the parameters of the latter because they are mathematically prescribed by these Godnames. Below is shown how the geometry of this subset S and its mirror image Ŝ, the subset of the 7 enfolded polygons making up the second half of the inner Tree of Life, embodies the dimension 248 of E8, the rank-8, exceptional Lie group appearing in E8×E8 heterotic superstring theory.
An object with a corners and b sides of c triangles has N geometrical elements, where N = a + b + c. For short, its geometrical composition will be written as (a, b, c).
|
A |
The 7 enfolded Type A polygons (S or Ŝ) contain 176 points, lines & triangles. They are the 41 corners and 88 sides of their 47 triangular sectors: (41, 88, 47). The 7th member of S or Ŝ is the dodecagon. Divided into its n sectors, an n-gon has (4n+1) geometrical elements: (n+1, 2n, n). The Type A dodecagon (n=12) has 49 geometrical elements: (13, 24, 12). The root edge separating S and Ŝ has the composition (2, 1, 0). Outside it, the dodecagon has (49−3=46) geometrical elements: (11, 23, 12). S or Ŝhas (176−46=130) geometrical elements: (30, 65, 35). When separate, S &Ŝ have (2×130=260=26×10) geometrical elements: (60, 130, 70). This 130:130 division of their 260 geometrical elements is a sign that S & Ŝ constitute a holistic system. Joined together at the root edge, they have 257 geometrical elements: (58, 129, 70), that is, 187 corners & sides, where 187 is the number value of Auphanim (Wheels), the Order of Angels assigned to Chokmah. |
||||
|
B |
The 7 enfolded Type A polygons making up each half of the inner Tree of Life have 264 yods when their 47 sectors are turned into tetractyses. Outside the root edge with 4 yods are 260 (=26×10) yods, i.e., the number of yods in 26 tetractyses. This shows how YAHWEH with number value 26 prescribes the number of yods needed to fill up and shape each half of the inner Tree of Life. Noting that the right-hand corner of the triangle coincides with the centre of the hexagon and that the right-hand corner of the pentagon coincides with the centre of the decagon, if the yods at these two corners are associated with the hexagon and decagon, the following 130:130 division of yods is displayed by the 7 enfolded Type A polygons:
|
||||
|
C |
The Type B n-gon has (15n+1) yods. The Type B dodecagon (n=12) has 180 yods surrounding its centre. Outside its root edge are (180−4=176) such yods. Notice that this is the number of geometrical elements in the 7 enfolded Type A polygons (see A). The holistic parameter 176 re-appears in a single polygon — the dodecagon — because this polygon is a holistic system on its own. Its 176 yods include 10 corners and 36 hexagon yods at centres of the 36 tetractyses. The number of yods other than corners that line tetractyses = 176 − 10 − 36 = 130. Outside the root edge of the two joined Type B dodecagons in the inner Tree of Life are (130+130=260) boundary yods other than their corners. If we add the two hexagonal yods in the root edge, there are 262 boundary yods other than corners of the dodecagons. This is the number of yods that can be associated with the 7 enfolded Type A polygons in each half of the inner Tree of Life. 131 boundary yods other than their corners can be associated with each dodecagon, where 131 is the number value of Samael, the Archangel associated with Geburah. The two separate Type B dodecagons have 264 boundary yods other than their corners. This is the yod population of the 7 enfolded Type A polygons. |
||||
|
D |
The Type B n-gon has 13n hexagonal yods. The Type B decagon (n=10) has 130 hexagonal yods. When separate and Type B, the penultimate members of the 7 polygons in each half of the inner Tree of Life contain (130+130=260) hexagonal yods. When joined, they have 256 hexagonal yods outside the root edge, where 256 = 44. This property illustrates the relationship between the Tetrad (4) and the Decad (10), symbolised by the decagon. |
Table of Godname numbers
| SEPHIRAH |
GODNAME |
NUMBER VALUE |
|
Kether Chokmah Binah Chesed Geburah Tiphareth Netzach Hod Yesod Malkuth |
EHYEH YAH, YAHWEH ELOHIM EL ELOHA YAHWEH ELOHIM YAHWEH SABAOTH ELOHIM SABAOTH EL CHAI ADONAI |
21 15, 26 50 31 36 26 + 50 = 76 26 + 103 = 129 50 + 103 = 153 49 65 |
The Godnames prescribe through their gematria number values the properties of the first 6 polygons and the first (6+6) polygons as a holistic subset of the inner Tree of Life:
HOW GODNAMES PRESCRIBE THE FIRST 6 OR THE FIRST (6+6) POLYGONS
Separate
Kether: 21
42 corners of the 36 sectors of the 1st 6 polygons (42 = 21st even integer);
Chokmah: 15
150 (15×10) geometrical elements in the 1st 6 polygons;
Chokmah: 26
26 corners of the root edge and the 1st 6 polygons outside their 6 sides that become the root edge when enfolded;
Binah: 50
50 corners of the root edge and of the 1st (6+6) polygons outside their 12 sides that become the root edge when enfolded;
Chesed: 31
31st integer after 1 = 32, which is the number of corners of the 1st 6 polygons that are either unshared with the outer Tree of Life or do not become their centres when they become enfolded;
Geburah: 36
36 corners and 36 sides of the 1st 6 polygons. 360 (36×10) hexagonal yods in the 1st (6+6) polygons;
Tiphareth: 76
76 corners, sides & independent centres of the 1st 6 polygons (the centres of the hexagon and decagon are corners of, respectively, the triangle and the pentagon);
Netzach: 129
129 geometrical elements in the root edge and in the 1st 6 polygons except their centres and their 6 sides that become the root edge;
Hod: 153
153 geometrical elements in the root edge and the 1st 6 polygons;
Yesod: 49
49th integer after 1 = 50, which is the number of "pure corners"* & sides in the 1st 6 polygons outside the root edge that are unshared with the Tree of Life;
Malkuth: 65
65th integer after 1 = 66, which is the number of corners of the 1st (6+6) polygons that do not coincide with corners of triangles in Tree of Life when they become enfolded.
Enfolded
| Kether: 21 |
21 corners of the 1st 6 polygons outside the root edge and unshared with the Tree of Life; |
| Chokmah: 15 |
165 hexagonal yods in the 1st 6 polygons, where 165 = 3×55 = 3×(12+22+32+42+52) = sum of 15 squares; 328 hexagonal yods in the 1st (6+6) polygons, where 328 = sum of first 15 prime numbers; 150 (15×10) yods outside the root edge line sides of tetractyses and surround centres of the 1st 6 polygons; |
| Chokmah: 26 |
26 corners of the 1st 6 polygons; |
| Binah: 50 |
50 corners of the 1st (6+6) polygons; |
| Chesed: 31 |
31 sides of the 1st 6 polygons. 127 geometrical elements outside the root edge (127 = 31st prime number); |
| Geburah: 36 |
360 (36×10) yods in the 1st (6+6) polygons other than the 2 endpoints of the root edge, the 12 centres of polygons and the 12 yods shared with the Tree of Life; |
|
Tiphareth: 76 |
76 yods lining sides of the 35 tetractyses in the 1st 6 polygons that are not sides of polygons outside the root edge; |
| Netzach: 129 |
129 sides of the 70 sectors of the 1st (6+6) polygons; |
| Hod: 153 |
153 yods unshared with the outer Tree of Life line the 35 tetractyses in the 1st 6 polygons; |
| Yesod: 49 |
49 corners & sides surrounding the centres of the 1st 6 polygons that are unshared with the outer Tree of Life; |
| Malkuth: 65 |
65 sides of sectors and 65 corners & triangles in the 1st 6 polygons; |
| Malkuth: 155 |
155 yods outside the root edge and intrinsic to the inner form of each Tree of Life line the 35 tetractyses. |
See Article 4, pp. 2-4 for more details.
* A corner is pure if it does not become the centre of a polygon when the separate polygons become enfolded. One of the corners of the triangle is impure because it becomes the centre of the hexagon in the enfolded set of polygons. Likewise, a corner of the pentagon is impure because it coincides with the centre of the decagon. These are the only impure corners.