| << Previous 1 [2] 3 4 5 ...40 Next >> |
#2 Correspondence between the outer Tree of Life and the tetrahedron
The five Platonic solids constitute the set of regular polyhedra that is mathematically complete in the sense that no more — and no less than — five such types of regular polyhedra can exist in three-dimensional space. Of course, not all finite sets of mathematical objects that are complete sets are holistic systems in the sense that they embody the divine archetypes in the universal blueprint governing the nature of matter. But the five Platonic solids do, indeed, constitute such a system. That is why their geometry is "sacred". That is why remarkable correspondences exist between their geometry and other sacred geometries, as this section will demonstrate.

As the simplest of the regular polyhedra, the tetrahedron is the seed, or starting point, in the five-stage development in the build-up of points equidistant in space that culminates in the dodecahedron, the last of the five Platonic solids. These steps are the polyhedral counterpart of the first five Sephiroth of Construction:
| Chesed | ↔ | tetrahedron |
| Geburah | ↔ | octahedron |
| Tiphareth | ↔ | cube |
| Netzach | ↔ | icosahedron |
| Hod | ↔ | dodecahedron |
The rhombic triacontahedron, which can be regarded as the foundation of the disdyakis triacontahedron because the latter is formed by sticking pyramids onto the 30 rhombic faces of the former, is the counterpart of Yesod, which literally means "foundation." The disdyakis triacontahedron, which is the outer form of the Polyhedral Tree of Life, is the counterpart of the last Sephirah, Malkuth, which is the material aspect of the Tree of Life blueprint.
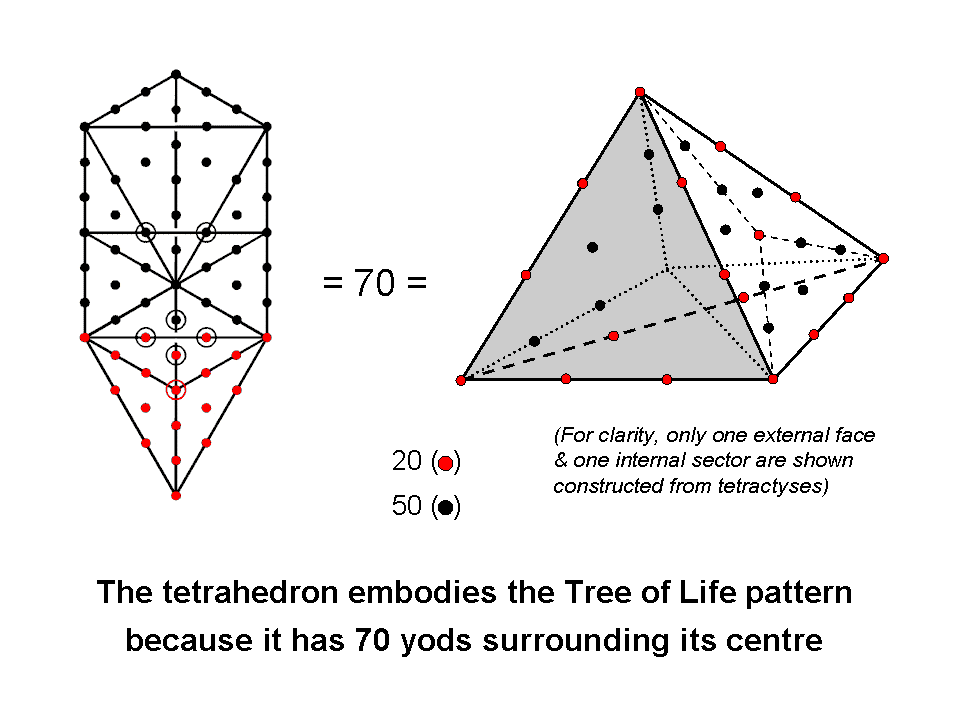
The Tree of Life is composed of 16 triangles. When they are turned into tetractyses, each with 10 yods, the total number of yods present is 70. Twenty red yods lie on the four faces of the tetrahedron whose vertices coincide with Malkuth, Yesod, Hod & Netzach. The rest of the Tree of Life has 50 black yods (the red & black circles in the diagram opposite denote yods behind other yods in the line of sight). This is the case n = 1 applied to the formula
Y(n) = 50n + 20
for the number of yods (Y(n)) in n overlapping Trees of Life. ELOHIM, the Godname of Binah with number value 50, prescribes both the number of yods in the Tree of Life that do not belong to its tetrahedron and the number of yods in successive Trees: Y(n+1) − Y(n) = 50.
Compare this with the tetrahedron. As it is a solid object, we have to consider the construction from tetractyses of its interior as well as its faces. Internally, it is composed of six tetractyses extending towards its centre from its six edges. They have 15 yods (14 black yods+centre) inside the tetrahedron. When its four triangular faces are divided into their 12 sectors and the latter then turned into tetractyses, 20 red yods (4 vertices, 16 hexagonal yods) either line the six edges of the tetrahedron or lie at the centres of its faces. 36 black yods lie on its faces within these edges. Hence, (14+36=50) black yods and 20 red yods, i.e., 70 yods, surround the centre of the tetrahedron. This 20:50 division of the 70 yods in the tetrahedron is the counterpart of the yod composition of the Tree of Life. In more detail, the correspondence is:
|
Tree of Life |
Tetrahedron |
| 20 yods in faces of tetrahedron. | 20 yods in faces. |
| 6 Sephiroth outside tetrahedron. | 6 yods at centres of interior tetractyses. |
| 12 centres of tetractyses outside tetrahedron. | 12 centres of tetractyses in faces. |
| 32 hexagonal yods on 16 sides of tetractyses outside tetrahedron. | 32 hexagonal yods on sides of tetractyses that are not polyhedral edges. |
| Total = 70 yods. | Total = 70 yods. |
Its construction from tetractyses reveals the tetrahedron to be the single, regular polyhedral counterpart of the Tree of Life. Notice how the Divine Names YAH with number value 15, ELOHIM (50) and ELOHA (36) prescribe aspects of the yod populations of the Tree of Life and tetrahedron (see Table 1). Including its centre, the tetrahedron is composed of 71 yods. 71 is the 36th odd integer, showing how ELOHA prescribes the simplest Platonic solid. For more examples of how Godnames determine properties of the tetrahedron, see Article 3 (WEB, PDF).
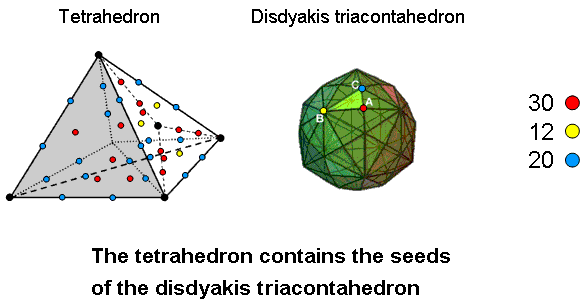
The tetrahedron contains the seeds of the disdyakis triacontahedron
Notice also in relation to the diagram above that the tetrahedron has, excluding its centre, eight black yods that
are corners of tetractyses and (70−8=62) hexagonal yods made up of 12 yellow hexagonal yods at
centres of tetractyses in its faces (for the sake of clarity, only those in one face are shown) and
50 hexagonal yods. The latter comprise 30 red hexagonal yods that are either on sides of
tetractyses in its faces (24) or at centres of internal tetractyses (6) and 20 blue hexagonal yods that are either
on its edges (12) or on internal sides (8). 62 is the number value of Tzadkiel, the
Archangel of Chesed. This 12:30:20 division reappears in the polyhedral form of the inner Tree of Life, namely, the
Catalan solid with 62 vertices (see here) called the "disdyakis triacontahedron" — as the 12 vertices
forming an icosahedron (called "B vertices" in various articles in the Articles section of this website), the 30 so-called "A vertices" (the
peaks of the pyramids whose bases are the 30 faces of the rhombic triacontahedron underlying the disdyakis
triacontahedron) and the 20 so-called "C vertices" of a dodecahedron. Here again is evidence that the
tetrahedron is the seed that grows eventually into the polyhedral form of the inner Tree of
Life.
Inner Tree of Life as the counterpart of the tetrahedron
The 8:62 division of yods in the tetrahedron created by the distinction between corners of
tetractyses and hexagonal yods manifests in the inner Tree of Life as:
1. the eight corners of the (7+7) enfolded polygons that coincide with the projections onto the
plane of these polygons of either Daath or Sephiroth, i.e., the two endpoints of the shared root edge and the six
corners outside it (shown below as black dots) that are shared with the outer Tree of Life;
2. the 62 corners outside the root edge that are intrinsic to the inner Tree of Life because
they are unshared with its outer form:
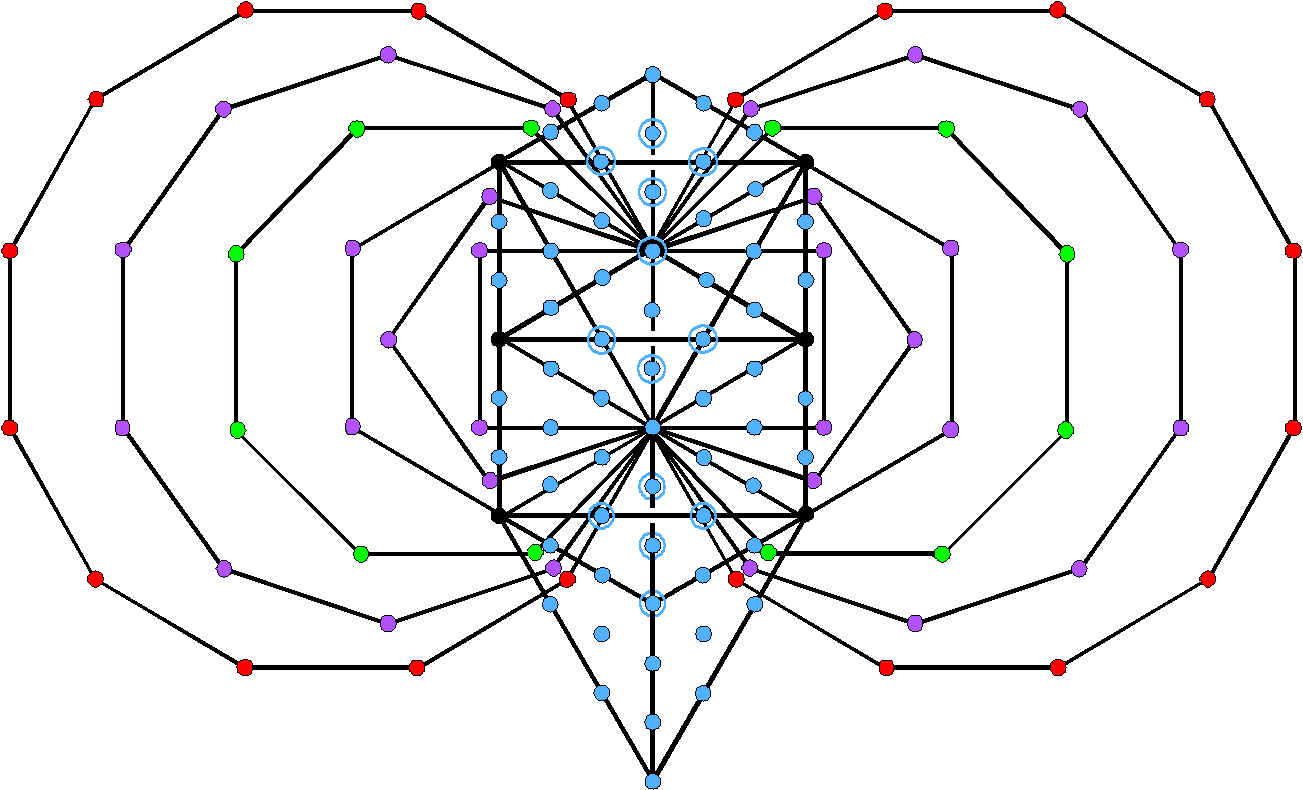
The latter comprise 20 red corners of the pair of dodecagons, 12 green corners of the pair of octagons and 30 purple corners of the square, pentagon, hexagon & decagon. This establishes the following correspondences between the inner Tree of Life, the tetrahedron and the disdyakis triacontahedron:
| Inner Tree of Life |
Tetrahedron |
Disdyakis triacontahedron |
||
|
12 green corners |
↔ | 12 hexagonal yods at centres of tetractyses in faces | ↔ | 12 B vertices of disdyakis triacontahedron; |
|
30 purple corners |
↔ | 30 hexagonal yods on sides of tetractyses in faces or at centres of internal tetractyses | ↔ | 30 A vertices of disdyakis triacontahedron; |
|
20 red corners |
↔ | 20 hexagonal yods either on edges of tetrahedron or on sides of internal tetractyses | ↔ | 20 C vertices of disdyakis triacontahedron. |
The 1-tree with its 19 triangles turned into tetractyses has 80 yods. It has (80−6=74) blue yods unshared with its inner form. They correspond to the 74 vertices of the so-called "144 Polyhedron," which is the polyhedral form of the outer Tree of Life (see here and Article 23 (WEB, PDF)). We see here how the inner and outer forms of the "Polyhedral Tree of Life" are encoded in its polygonal counterpart.
| << Previous 1 [2] 3 4 5 ...40 Next >> |