
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://www.smphillips.mysite.com
“Change has an absolute limit:
This produces two modes;
The two modes produce four forms,
The four forms produce eight trigrams;
The eight trigrams determine fortune and misfortune."
Confucius (commentary on the I Ching)“I am the One who becomes Two,
Who becomes Four,
Who becomes Eight,
And then I am One again.”
Coffin of Petamon
(Ancient Egyptian text)
Abstract
The eight trigrams of the ancient Chinese divinatory system of I Ching represent stages or phases of universal cycles. In Kabbalah, they correspond to Daath and the seven Sephiroth of Construction of the Tree of Life. Their generation from the interaction of yang and yin leads to their natural division into two sets of four. This reflects the ancient view of the number 8 as 2×4. An example of such doubling is how, as the product of two identical groups E8, the gauge symmetry group E8×E8 of heterotic superstrings has a dimension 496 that is embodied in an octagon, whose eight corners are those of two squares rotated through 45°. This geometrical property has an arithmetic counterpart that is manifested in the sacred geometry of the Tree of Life. Another example of the universal 4:4 pattern in nature are the eight Gregorian musical modes, which consist of four authentic modes and four plagal modes. These eight octave species constitute a cycle of successive sequences of seven intervals spanning the Pythagorean scale. Moreover, comparison between these patterns and their trigram counterparts indicates that the only ordering of musical scales consistent with I Ching is the traditional Church one, although their ancient Greek names are wrong. Comparison of the average distances of the planets predicted by the author’s modified Titus-Bode Law with the population of yin/yang lines in the I Ching table indicates that the octet of planets Mercury–Uranus splits into two groups of four, the distances spanned by each set being geometrically embodied in the inner form of the Tree of Life. Other examples of eight-fold cycles include the eight stages in the cycle of the cell leading to its division into two daughter cells.
1
1. I Ching’s origins and the Tree of Life
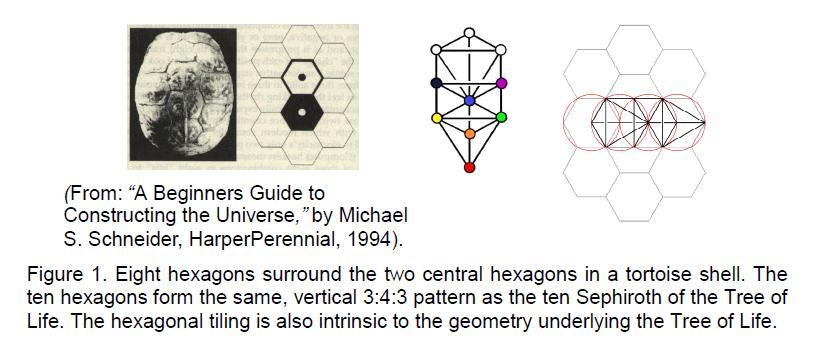
When the historical origins of any religion are examined, it is often difficult (if not impossible) to separate fact from mythology. However, as in the case of the ancient oracular system known in the West as I Ching, the two may sometimes coincide. The scholar Kung Mgan-Kwoh in the second century B.C.E credited Fu Hse, the first Chinese emperor, with its discovery in the following legend: as he was meditating one day by the River Ho (the Yellow river), Fu Hse noticed a tortoise climb out of the river. Examining the pattern of lines on the creature’s scales, he had a flash of insight. The shell of a tortoise (Fig. 1) consists of tessellating hexagons, each one surrounded by six others.
Two hexagons are arranged centrally on the top of the shell and are surrounded by eight other hexagons.
According to Taoist philosophy, yang and yin, respectively, the positive, active and negative, reactive phases of nature’s great cycles, emerged from Tai Yi, the “Great Unity,” symbolized by a circle. As opposite states represented by the positive (+) and negative (–) signs, they can be paired in four ways: + +, – +, + – & – –.
2
(Fig. 2). Adding a plus or minus sign at the end creates eight possible combinations:
plus sign: + + +, – + +, + – +, – – +,
minus sign: + + –, – + –, + – –, – – –.Fu Hse took the central pair of hexagons to be a symbol of the principles of yang and yin and realized that the eight hexagons surrounding them represented the eight possible triple combinations of yang and yin attributes. This would mean that there would be eight different sets of three elements, where each is in either a yang or a yin state. In the divinatory context of I Ching, the eight outcomes of three successive steps that each allows the same two possibilities are known as ‘Kwa,’ or ‘trigrams.’ Single lines symbolize yang and broken lines symbolize yin. Plus and minus signs are read from left to right and corresponding lines in trigrams are read from top to bottom.
Figure 1 shows that the ten hexagons are arranged in the same way as the ten Sephiroth on the Tree of Life. The three vertically aligned hexagons on the left correspond to Binah, Geburah and Hod on the left-hand Pillar of Judgement, the three hexagons on the right correspond to Chokmah, Chesed and Netzach on the right-hand Pillar of Mercy and the four hexagons in the middle column correspond to Kether, Tiphareth, Yesod and Malkuth on the central Pillar of Equilibrium. The upper member of the pair of hexagons in the middle of the tortoise’s shell symbolized yang; it corresponds to Tiphareth. The lower member shown in black to symbolize yin corresponds to Yesod.
Their similar arrangement might be thought to be fortuitous. However, it is hardly surprising that a geometrical pattern that is similar to the Tree of Life should, when contemplated upon by someone in a meditative state, activate deep insights into nature. After all, Indians have mediated upon mandalas with the same purpose for thousands of years. Moreover, the pair of hexagons symbolizing for Fu Hse the yang and yin polarities in nature has properties that similarly match those of the Tree of Life, as now explained. The four stages in the creation from unity of the eight hexagrams is an example of the Pythagorean teaching that, whatever its particular realisation, the wholeness of God unfolds in four steps represented by the four rows of the tetractys:
3
Each of the ten dots of the tetractys will be called a ‘yod,’ which is the name of the tenth letter of the Hebrew alphabet. When the 16 triangles making up the three-dimensional Tree of Life are turned into tetractyses, they are found to comprise 70 yods. Just as the yods in each row of the tetractys signified for the Pythagoreans the point, the two endpoints of a line, the three corners of a triangle and the four corners of a tetrahedron — the emergence of form from the dimensionless point — so the ten Sephiroth of the Tree of Life are arranged in a similar, geometrical sequence. This so-called ‘trunk’ of the Tree of Life contains 35 yods (Fig. 3). Hence, there are also 35 yods outside its trunk. Its geometry implies a hidden, geometrical object discovered by the author and called its inner form. It consists of two identical sets of seven regular polygons:
triangle, square, pentagon, hexagon, octagon, decagon, dodecagon.
Each set has 36 corners, 35 corners being associated with either set. The hexagon is the fourth regular polygon:
1
2
3
4triangle
square
pentagon
hexagonAccording to the Pythagorean principle mentioned earlier, it therefore has special significance in nature. Examples are the hexagonal benzene molecule serving as the template of aromatic hydrocarbons and the hexagonal groupings of baryons and mesons predicted by the theory of quarks.1 Its status is confirmed by the fact that the pair of hexagons in the inner form of the Tree of Life is found to possess
70 yods when their sectors are converted into tetractyses (Fig. 4), i.e., one hexagon with 35 associated red yods corresponds to its trunk, whilst the other hexagon has the same number of black yods as those lying outside the trunk. Notice also that the shapes of both objects are marked out by ten points, leaving 60 yods in either case generated by the transformation of their triangles into tetractyses. The mirror symmetry of each half of the inner Tree of Life is what expresses the yang-yin polarity. This is embodied in its outer form as its two side pillars, headed by Chokmah, one of whose Kabbalistic titles is Abba (“Great Father”), and by Binah, one of whose titles is Aima (“Great Mother”).
According to Kabbalah, three factors were hidden within the three Veils of Negative Existence from which the ten Sephiroth emanated. They were the Zahzahot, or the three Hidden Splendours. These principles determined the three pillars of the
4
Tree of Life symbolising the active, passive and balanced Sephirothic qualities. Their counterparts in the I Ching are the three rows of a trigram.
Tai Yi, the “Great Unity,” is Kether, the first Sephirah, embodying Divine Unity. They are represented in both Kabbalah and Taoism by a circle. This bifurcates into the duality of the male, generative or life-giving principle, corresponding to Chokmah and to yang, and the female, reproductive or formative principle, which corresponds to Binah and to yin. This is shown in Fig. 5 by the line and broken line next to
these Sephiroth. With successive interplays of these fundamental principles, starting with the Heaven trigram denoting maximum yang quality, all seven Sephiroth of Construction ensue, the Earth trigram that corresponds to Malkuth (the physical universe) expressing maximum yin. The last four hexagrams result from the first four by interchanging yang and yin lines:
This will be discussed later in the context of the Church musical modes. From a Kabbalistic perspective, this switch over due to progressive reversals of polarity corresponds to the division of the Tree of Life into the Upper Face (Kether-Tiphareth) and the Lower Face (Tiphareth-Malkuth). As mirror to the Upper Face, the Lower Face is always subjective or passive — the personality or ego is the creation and vehicle of the Higher Self at Tiphareth, the centre of the Tree of Life map of consciousness.
5
Table 1. Gematria number values of the ten Sephiroth in the four Worlds.
ANGELS
CHAKRA1 Kether
(Crown)
620EHYEH
(I am)
21Metatron
(Angel of the Presence)
314Chaioth ha Qadesh
(Holy Living
Creatures)
833
Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
6362 Chokmah
(Wisdom)
73YAHWEH, YAH
(The Lord)
26, 15Raziel
(Herald of the
Deity)
248Auphanim
(Wheels)
187Masloth
(The Sphere of
the Zodiac)
1403 Binah
(Understanding)
67ELOHIM
(God in multiplicity)
50
Tzaphkiel
(Contemplation of God)
311
Aralim
(Thrones)
282
Shabathai
Rest.
(Saturn)
317Daath
(Knowledge)
4744 Chesed
(Mercy)
72EL
(God)
31Tzadkiel
(Benevolence of God)
62Chasmalim
(Shining Ones)
428
Tzadekh
Righteousness.
(Jupiter)
1945 Geburah
(Severity)
216
ELOHA
(The Almighty)
36
Samael
(Severity of God)
131
Seraphim
(Fiery Serpents)
630
Madim
Vehement
Strength.
(Mars)
956 Tiphareth
(Beauty)
1081
YAHWEH ELOHIM
(God the Creator)
76Michael
(Like unto God)
101
Malachim
(Kings)
140
Shemesh
The Solar Light.
(Sun)
6407 Netzach
(Victory)
148
YAHWEH SABAOTH
(Lord of Hosts)
129
Haniel
(Grace of God)
97Tarshishim or
Elohim
1260
Nogah
Glittering
Splendour.
(Venus)
648 Hod
(Glory)
15
ELOHIM SABAOTH
(God of Hosts)
153
Raphael
(Divine Physician)
311
Beni Elohim
(Sons of God)
112
Kokab
The Stellar Light.
(Mercury)
489 Yesod
(Foundation)
80
SHADDAI EL CHAI
(Almighty Living God)
49, 363Gabriel
(Strong Man of God)
246
Cherubim
(The Strong)
272
Levanah
The Lunar Flame.
(Moon)
8710 Malkuth
(Kingdom)
496
ADONAI MELEKH
(The Lord and King)
65, 155Sandalphon
(Manifest Messiah)
280Ashim
(Souls of Fire)
351
Cholem Yesodoth
The Breaker of the
Foundations.
The Elements.
(Earth)
168
6
2. The octad as 2×4
As Fig. 2 shows, the sequence of eight trigrams is built up in four stages. The four pairs of yin/yang lines, or Hsiang, create two sets of four trigrams — one set by the addition of a yang line and the other set by the addition of a yin line. As trigrams symbolise not things but ever-changing phases of a cycle (these may, of course, correspond to different objects), the sequence is better represented by the figure-eight flow chart shown in Fig. 6. Starting with the Heaven trigram at the top of the octagon and labelled ‘0,’ the next three stages 1, 2 & 3 are passed through (indicated by the blue flow curve), then it crosses over the centre of the octagon to trigram 4, flowing through 5 and 6 to trigram 7 (indicated by the red flow curve) and, finally, returning vertically through the centre again to the starting point 0 to commence another cycle. The curves of the Tai Chi symbol reproduce these flow lines. The very Arabic numeral for the number 8 aptly represents the flow. Laid on its side, it is the mathematical symbol for infinity. However, this symbol measures quantity; it does not symbolize the indefinite duration of cyclic activity. A more appropriate term that the closed loop signifies would be perpetuity.
In the context of I Ching, the number 8 has a natural factorization as 2×4. According to Michael Schneider in his “A Beginner’s Guide to Constructing the Universe”: “The Indo-European names for “eight” emphasize it as a “doubling of four,” most deriving from the Sanskrit o-cata-srah (“twice four”), which became okta in Greek and octo in Latin. These references to one, two, and four tell us that the archetype of eight, called Octad, weaves together the principles of Monad’s unity, expansion, and cycles, Dyad’s polarity, and tetrad’s materialization, that is, material forms precipitate from their archetypes through polarity and pulsing cycles.”2 Referring to this number, W. Wynn Westcott in his “The Occult Power of Numbers” said “The Greeks thought it an all-powerful number; they had a Proverb ‘all things are eight.’”3 One of the titles given to the number 8 by the ancient Pythagoreans was “All Harmonious.” This referred to their understanding that it measures a complete cycle. For example, the eight notes of the musical scale span a complete octave and every eighth day of a week is the same one.
The Kabbalistic significance of the octagon is that, when its sectors are converted into tetractyses (Fig. 7), it is found to contain 49 yods, where 49 is the number value of the Godname El Chai assigned to Yesod (Table 14). This property of the octagon is a sign that it embodies a number of universal importance. This number is revealed by considering the next higher-order generalisation of the tetractys (the 1st-order tetractys), namely, the 2nd-order tetractys (Fig. 8). An octagon whose sectors are 2nd-order tetractyses has 80 corners of 1st-order tetractyses surrounding its centre and 496 coloured yods (Fig. 8). Each yod denotes one of the 496 10-dimensional gauge fields of the gauge
7
8
symmetry group E8×E8 governing the unified interactions of heterotic superstrings. The number value 80 of the Sephirah Yesod is the number of 1st-order tetractyses making up the octagon. As a square has half the number of sides of an octagon, it contains 496/2 = 248 coloured yods when its four sectors are transformed into 2nd-order tetractyses. 248 is the number of gauge fields of the superstring gauge symmetry group E8.
The ancient view of the number 8 as twice four was a profound insight that has manifested again in modern times in superstring theory, for the discovery that the heterotic superstring gauge symmetry group is the product of two identical groups simply reflects the geometrical fact that the corners of two similar squares rotated through 45° coincide with the corners of an octagon, that is, that 8 = 2×4.
The superstring number 496 is connected to the number 8 arithmetically as well as geometrically through its tetractys encoding in the octagon. It is known to mathematicians as the third, so-called ‘perfect number.’ This type of number is one whose factors (including 1) add up to the number itself. For example, 6 is the first perfect number because 6 = 1 + 2 + 3, where 1, 2 and 3 are the factors of 6, and 28 is the second perfect number because 28 = 1 + 2 + 4 + 7 + 14, where 1, 2, 4, 7 and 14 are its factors. As shown in Fig. 10a, 496 has eight factors other than 1 that can be assigned to the corners of an octagon. Moreover, these factors group naturally into two sets of four: (2, 4, 8, 16) and (31, 62, 124, 248) (Fig. 10b). Each set can be assigned to the corners of a square. Again, the number 8 splits into two 4s. The numbers of divisors other than 1 (that is, non-trivial ones) for the first three perfect numbers 6, 28 and 496 are 2, 4 and 8:
These are the very digits in 248 — the dimension of the gauge symmetry group E8!
9
10
As shown in Fig. 2, the eight trigrams are built up in four stages, starting with Tai Yi, the “Great Unity.” As discussed in Article 18, the I Ching table of hexagrams is built up in (4+4) stages. Starting with the eight trigrams (Fig. 11), the fifth stage is the addition of the Ch'ien trigram to each to form the first row of hexagrams. The sixth stage is the addition of the Ch' ien and Tui trigrams to form the first two rows of hexagrams, then the seventh stage is the addition of the Ch' ien, Tui, Li and Chen trigrams to form the first four rows and, finally, the eighth stage is the addition of all eight trigrams to form the I Ching table itself. The 4:4 division in the eight trigrams results from
interchanging yang and yin lines, so that, as displayed in Fig. 5, trigrams at the corners of an octagon and diametrically opposite each other are polar opposites. The first four trigrams are the essential ones because the last four result from interchanging yang and yin lines. The 4:4 division in the eight stages of creation of the table of hexagrams reflects the distinction between the whole table and the eight trigrams as its building blocks. In both cases, we see that the first four stages generate the basic set of trigrams.
Figure 12 indicates how the square and the octagon are present in the geometry of the Tree of Life. Its inner form consists of two sets of seven regular polygons, each set having 36 corners. The Godname Eloha of the Sephirah Geburah with number value 36 prescribes each
half of the inner Tree of Life. If the first eight integers are assigned to the corners of an octagon (Fig. 13), the sum (20) of the first four even integers at the corners of a square is the number of corners of the decagon and dodecagon and the sum (16) of the first four odd integers at the corners of a second square is the number of corners of the triangle, square, pentagon, hexagon and octagon.
11
The lowest Tree of Life of any set of overlapping Trees of Life (the ‘1-tree’) has 19 triangles. If these are transformed into tetractyses, they comprise 80 yods. This is the number of corners of the 94 triangular sectors of the two sets of seven, enfolded regular polygons (Fig. 14).
If the first eight odd integers after 1 are assigned to the corners of an octagon, their sum is 80. The four integers arranged in one square add up to the number (44) of corners of the 50 sectors of the two sets of the first five polygons and the four integers at the corners of the other square sum to the number (36) of corners of the 44 sectors of both pairs of the last two polygons (Fig. 15). Whether the
first eight integers or the first eight odd integers are considered, their separation into two sets of four creates sums that differentiate the first five polygons from the last two polygons.
The sum of the first six odd integers after 1 is 48. This is the number of Kokab (Mercury), the Mundane Chakra assigned to Hod. It is the number of yods in the 1-tree up to Chesed, the first Sephirah of Construction. In other words, the emanation of the seven Sephiroth of Construction generates 48 yods. Therefore, the sum (32) of the two last odd integers 15 and 17 in Fig. 15 is the number of yods above Chesed.
12
The seven separate polygons have 48 corners. Two squares rotated through 45° require 48 yods to delineate their boundary (Fig. 16).
The reason for this beautiful harmony between number and the sacred geometry of the Tree of Life and its inner form is that a Divine Name — El Chai — is associated with the octagon, its number vale of 49 being the number of yods in this polygon when divided into tetractyses. No wonder that the Pythagoreans called the octad “All Harmonious”!
3. I Ching & the eight Church musical modes
The Pythagorean octave of eight musical notes is spanned by successive intervals of a perfect fifth and a perfect fourth.
or Ascending descending the scale through these two intervals generates the same note an octave higher or lower. Played in succession, these two intervals therefore complete a musical cycle, whatever the note that was played first. They may be regarded as the yang and yin phases of a cycle that ends on the same note, albeit higher or lower in pitch by one octave. Rather than make any assumptions about the ‘masculine’ or ‘feminine’ characters of these intervals, we shall use the convention that a perfect fifth is the yang phase and the perfect fourth is the yin phase (Fig. 17). Yang and yin have equal and complementary status and neither musical interval can be said to be the more fundamental.
The octave C-C' can be divided into either four perfect fourths or four perfect fifths (Fig. 18).
Compare this with how the eight trigrams consist of two sets of four, one set being derived from the other by interchanging yang and yin lines:
13
The same 4:4 division is found in the intervals of the notes of the Pythagorean scale as with the eight trigrams. This is evidence of course that this scale is truly the fundamental musical scale, unlike many of its more modern imitations.
It was argued in Article 165 that the current view held by many musical scholars that the ancient Greek musical modes were not octave species but different keys of the same scale is wrong. Two reasons were given:
The Pythagorean scale consists of five tone intervals T of 9/8 and two leimmas L of 256/243 (the modern semitone):
T T L T T T L
By starting successive sequences of intervals displayed in Figure 19 on the circumference of a circle, it is readily seen that there can be only seven different octave species:
L T T T L T T
T T T L T T L
T T L T T L T
T L T T L T T
L T T L T T T
T T L T T T LDorian (mode 1)
Phrygian (mode 3)
Lydian (mode 5)
Mixolydian (mode 7)
Hypodorian (mode 2)
Hypophrygian (mode 4)
Hypolydian (mode 6)The three ‘hypo’ versions of the Dorian, Phrygian and Lydian modes are separated from the latter by a perfect fourth (Fig. 20).
14
The Roman Catholic Church added an extra mode called the Hypomixolydian (mode 8) to be the counterpart of the Mixolydian. It is the same octave species as the Dorian but has a distinct ethos because its finalis (ending note) and dominant (reciting note) are different. Figure 21 shows the four Authentic Modes and the four Plagal Modes.
The double-headed arrows link an Authentic Mode and a Plagal Mode whose patterns of intervals are mirror images of each other.
15
Two modes — the Dorian and the Hypomixolydian — are trivial mirror images of each other because their identical sequences of intervals are mirror images of themselves (T = tone interval, S = semitone):
Fig. 22 is a three-dimensional way of depicting the mirror symmetry of the eight Church modes. Along each of three great circles of a sphere, spaced 60° apart, are eight points denoting the eight notes of the Phrygian, Lydian and Mixolydian modes, the South Pole of the sphere denoting the tonic and the North Pole denoting the octave.
Along the vertical axis of the sphere between the poles are six red points representing the six notes between the tonic and the octave of the Dorian mode. As the Hypomixolydian mode has the same notes as the Dorian mode, its notes are represented by the same points. These are depicted in Fig. 22 as red circles. Points on a great circle representing a note of a mode and its counterpart in the mirror image of that mode are diametrically opposite each other.
16
The eight modes with the same tonic consist of 50 notes. This is the number value of Elohim, the Divine Name assigned to Binah. This is a very important property because it shows that the eight Church modes form an archetypal musical pattern even though the Hypomixolydian mode — the last mode — has the same interval pattern as the Dorian mode — the first mode. It amounts to the difference between the first seven notes and all eight notes completing the cycle of the octave. The eight modes conform to the Tree of Life blueprint because the two sets of the first six of the seven enfolded polygons constituting the inner Tree of Life have 50 corners (Fig. 23), the 24 corners on one side symbolizing the notes of the Authentic Modes between the tonic and the octave and the 24 corners on the other side symbolizing the corresponding plagal notes. The four Authentic modes correspond to the Ch’ien, Tui, Li and Chen trigrams and the four plagal modes — their mirror images — correspond to the Sun, K’an, Ken and K’un trigrams — the counterparts of the first with yang and yin lines interchanged. The Heaven trigram corresponds to the Dorian mode, the Earth trigram corresponds to the Hypomixolydian mode and — very interestingly — the seventh trigram (Ken) corresponds to the Hypolydian mode, which is the Pythagorean scale. In other words, the last trigram before the end of the cyclic sequence of trigrams has as its counterpart the mathematically perfect Pythagorean scale. The fact that in the Church classification it turns out to be a plagal mode, not (as would be expected of such an influential musical scale), an authentic mode, demonstrates the errors of nomenclature in the Gregorian modes. This can be seen independently by comparing the known ethos of some ancient Greek modes with those of Church modes with the same name: they do not match.7
Is it necessary to follow the Church numbering system for modes that start with the Dorian mode? After all, this mode might have been chosen by human beings for merely historical reasons, being the scale that was most favoured by Plato for playing music in his ideal society. It might not be what God conceived. Indeed, how can a particular mode be deemed to generate all the others when the ring of intervals shown in Fig. 19 favours no starting point? As now shown, comparison of the 4:4 system of modes with the eight trigrams upholds the traditional list that starts with the Dorian mode.
If any musical scale might be considered most apt to start the sequence of modes, it would have to be, of course, the Pythagorean scale in view of its being the C scale. Suppose that it corresponds to the first trigram, then (considering the possibilities of either ascending or descending scales):
Whether the scale ascends or descends, two scales in the same quartet (shown above linked by brackets) are mirror images of each other. The Pythagorean scale cannot therefore correspond to the first trigram. In view of the way the ancient Greeks understood octaves to be created from two tetra chords, let us next suppose that the Pythagorean scale corresponds to the fourth trigram. Then:
In either case, two scales belonging to the same set of four are mirror images, whereas
17
what is wanted is that only scales belonging to different sets of four be mirror images. This means that the Pythagorean scale cannot correspond to the fourth trigram. Finally, suppose that it corresponds to the seventh trigram. Then either (case A):
or (case B):
Case B is forbidden because pairs of sequences of intervals that are mirror images belong to the same set of four scales. In case A, however, the interval patterns corresponding to the first four trigrams are the mirror images of those corresponding to the last four trigrams. This is the required result.
There is therefore only one possible scheme of correspondence between trigrams and scales that permits mirror symmetry in both. The Heaven trigram with three yang lines has to correspond to the Dorian mode and the Earth trigram with three yin lines must correspond to the Hypomixolydian mode. These two trigrams are special in that they are the first and last of the trigrams. Their corresponding modes are also special in that, as well as being mirror images of each other, their interval patterns are also mirror images of themselves. Although the early musical theorists erred in their naming of the Gregorian modes after the ancient Greek modes, they were correct in the way they ordered
them. Far from being a matter of arbitrary choice, there is only one ordering of octave species that is consistent with the sequence of generation of trigrams and which preserves the correlation between mirror image patterns of intervals and symmetry with respect to interchange of yin and yang lines. It starts with the mirror-symmetric Dorian mode.8
Figure 5 shows that trigrams at the corners of the octagon that are diametrically opposite each other have, as representations of binary numbers, the following integers as their values:
0
1
2
37
6
5
4Number values of trigrams opposite each other always add up to 7. The Pythagoreans
18
regarded the odd integers as male and the even integers as female. Although the ‘gender’ of each integer alternates as one goes through the sequence of trigrams lying on the figure-of-eight (Fig. 25), pairs of integers diametrically opposite each have opposite polarity. Although the ethos attributed by the ancient Greeks to their musical modes is poorly known and contradictory, some of their characteristics do fit this alternating pattern. Phrygian music was exciting and passionate, generating a masculine energy, whilst the Lydian mode was thought a ‘wailing mode suitable for women.’ However, if strictly pursued, this would make the Hypolydian mode a feminine mode because it corresponds to the even integer 6. Music played according to the Pythagorean scale does not have feminine emotional qualities. As one might expect, it is clearly wrong to assign psychological qualities to modes based merely upon the genders that the ancient Pythagoreans assigned to even and odd integers!
4. The planetary octet
It was shown in Article 179 that the two assumptions:
led to a modified form of the famous Titius-Bode Law governing distances of planets from the Sun that accurately applies to Neptune and Pluto as well, unlike the earlier version. The predicted average distances (in terms of 1/10 A.U.) of the planets from the asymptotic centre of the spiral, Mercury and the Sun are:
The first eight planets Mercury–Uranus group into an octet. The three planets Uranus–Pluto are the first three members of a second octet whose mean distances from Uranus are determined by the same mathematical relation as that governing the distances of the first octet of planets from the asymptotic centre, albeit with different parameters. Notice that the values of n appearing in the Titius-Bode Law for the distance:
of the nth planet after Mercury in the first octet are the same as the number values of the seven trigrams after the Heaven trigram shown in Fig. 5. Mercury plays the role of the tonic of the musical octave. Just as its pitch can have any value that, once fixed, determines the pitches of the remaining notes, so the average distance of Mercury from the Sun is a free variable* that is not part of the geometric series:
3, 6, 12, 24, 48, 96, 192
______________________________
*In the author’s theory modifying this law, it ceases to be an ad hoc constant but becomes predicted.19
occurring in the Titus-Bode Law. This series determines the average distances of the planets not from Mercury, as has always been assumed by astronomers, but from the asymptotic centre of the logarithmic spiral-shaped planetary nebula that spawned the Solar System. This explains why the mathematical equation for Dn given above could accommodate Mercury only by assuming for it the singular value n = –∞. Astronomers have not realized that this determines the position of the asymptotic centre of a logarithmic spiral that doubles in size with every revolution, i.e., that the Titius-Bode numbers refer actually to the distance of planets from this centre, not from Mercury.
Just as the 64 hexagrams of the I Ching table build up in two sets of four stages
20
(Fig. 11), so the average distances of the octet of planets from the asymptotic centre, which are the numbers of yin and yang lines in the trigrams making up these stages (Fig. 26), group into two sets:
3
6
12
96
48
24
The average distances of these planets from Mercury are 4, 7, 13, 25, 49, 97 and 193. The fourth ‘planet’ after Mercury is the Asteroid Belt with an average distance of 25 (actually 23.8) and the average distance between this and Uranus, the last member of the octet, is 168 (actually, 164.2). This pair of distances is encoded in the first six regular polygons enfolded in the inner form of the Tree of Life because, when their 35 sectors are converted into tetractyses, one finds that there are 25 corners of polygons and 168 other yods associated with these polygons (Fig. 27).
The distinction between the shape-marking corners and the other yods corresponds to the ‘turning of the corner’ at the Asteroid Belt, which plays the role of the perfect fifth G of the Pythagorean scale:
As Fig. 24 indicates, this corresponds to the completion of the eight trigrams with 24 yang and yin lines. The completion of the octet of planet spans a further distance of 168. This is the number of additional yang and yin lines need to construct the first half of the I Ching table. The number of lines in the whole table is 384, which is the average distance of the last planet Pluto from the asymptotic centre predicted by the logarithmic spiral theory.
21
22
This is simply the number of yods in both sets of six polygons other than the two endpoints of the root edge (Fig. 28). Alternatively, there are 384 yods intrinsic to each pair of six polygons enfolded in successive, overlapping Trees of Life. This property is a remarkable demonstration of the precise correspondence or isomorphism between the Tree of Life and its Chinese counterpart — the 64 hexagrams of the I Ching.
The square embodies the numbers 25 and 168 both geometrically and arithmetically.
23
The square with its four sectors turned into tetractyses has 25 yods, whilst the twelve odd integers 3, 5, 7, …25 lying on the sides of a square, four to a side, add up to 168:
The number 168 is the number value of Cholem Yesodoth (“breaker of the foundations”), the Mundane Chakra assigned to Malkuth and astronomically represented by the planet Earth. Its fundamental significance as the structural parameter of superstrings has been discussed in many earlier articles by the author.
The number 25 is the number of spatial dimensions predicted by quantum mechanics for spinless strings. Embodied in the distances spanned by the four planets after Mercury (formally regarding the Asteroid Belt as a planet) and by the last four planets of the octet are, respectively, the dimension of space and the number of circularly polarised oscillations made by each of the ten closed, string-like whorls constituting the subquark state of a superstring during one-half of its revolution.10
Figure 29 lists examples of the eight-fold character of biological, astronomical, musical and subatomic systems. The eight stages of activity in the life of a cell are as follows:
1. Interphase: cell grows and performs other life processes
cell rests (no division)
cell enlarges, produces RNA and synthesizes protein
chromosomes replicate
centrioles replicate, cell growsMitosis (cell division) begins at the end of Interphase.
2. Prophase: nucleolus fades/chromatin (replicated DNA and associated proteins) condense into chromosomes/centrioles migrate into opposite sides of cell/spindle fibre network form;
3. Prometaphase:nuclear envelope disintegrates/some mitotic spindle fibres elongate from the centrioles and attach to kinetichores, protein bundles located on the chromosomes;
4. Metaphase: spindle fibres attach to chromosomes at kinetichores/chromosomes align on metaphase plate;
24
5. Anaphase: spindle fibres shorten/kinetichores separate/chromatids (daughter chromosomes), pulled apart by contracting fibres, move to opposite poles/poles move apart;
6. Telophase: daughter chromosomes arrive at poles/spindle fibres disappear/nuclear envelope reforms (this is the completion of mitosis);
7. Cytokinesis: cell pinched into two daughters by ring of actin protein/microtubules reorganise into new cytoskeleton;
8. Interphase.
Figure 30 displays the cyclic nature of the life of a cell. Notice that the crossing over to the Anaphase stage marks the separation of pairs of chromosomes to opposite sides of the cell. Once again, the eight stages of a cyclic sequence are divided into two sets of four. In the Anaphase, Telophase and Cytokinesis stages, there is physical movement of the DNA material and splitting of the cell. This 4:4 differentiation corresponds to the division of the eight trigrams into two sets of four:
with the Sun trigram (the fifth one in the sequence) corresponding to the Anaphase. One may characterize the first four stages as the yang-dominated part of the cycle and the remaining stages as the yin-dominated, formative phase.
The eight unit octonions ei and their relation to the eight zero roots of the superstring gauge symmetry group E8 were discussed in Reference 7 and in Article 15.11
Finally, the most obvious manifestation of the pattern of twelve yang lines and twelve yin lines of the eight trigrams is the Earth’s day of 24 hours, which is divided at the spring and autumn equinox into twelve hours of sunlight and twelve hours of night. For the ancient Chinese, light was yang and darkness was yin. The 12:12 division of lines in the two sets of four trigrams is represented in the last pair of polygons making up the inner form of the Tree of Life — the pair of mirror-image dodecagons, each of which has twelve corners. This
polygon is associated with the last Sephirah, Malkuth, because it embodies the number value 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth, 168 yods other than corners of the dodecagon surrounding the centre when each sector
25
is divided into three tetractyses (Fig. 31). That this is not a coincidence is indicated by the fact that the sum of the twelve odd integers after 1 that can be assigned to the corners of a dodecagon is also 168. For triple division of a sector, this polygon is unique12 in having such a property (in the case of each sector being a tetractys, the triangle — the simplest polygon — uniquely has this property). The cycle of seven days of the week lasts for 7×24 = 168 hours. The dodecagon therefore embodies the numbers of hours in both a day and a week. The
twelve yang lines correspond to one dodecagon and the twelve yin lines correspond to its counterpart in the mirror-image set of seven polygons making up the inner form of the Tree of Life. Yang/yin polarity is incorporated in this universal blueprint through the two chiral sets of seven polygons.
At the beginning of this article, it was pointed out that a pair of adjoined hexagons is isomorphic to the Tree of Life because both contain 70 yods, of which ten are corners. When their sectors are divided into three tetractyses, 168 yods are generated (Fig. 32). This fundamental superstring structural parameter is therefore embodied in the very pair of hexagons that the first Chinese emperor Fu Hse realised symbolised yang and yin when he noticed it in the pattern of scales on the shell of a tortoise.
We saw earlier that the eight trigrams have their astronomical counterpart in the first eight planets of the Solar System, which complete an octet. The Titius-Bode distances of these planets from the asymptotic centre of the logarithmic spiral:
24
centreAsteroid
Belt24
168

imply that the Asteroid Belt (the fourth ‘planet’ after Mercury) is 24 units from this centre and that Uranus (the last member of the octet and the fourth from the Asteroid Belt) is 168 units from the latter. The lengths of the Earth’s day (24 hours) and week (168 hours) cannot be based upon arbitrary man-made units of time when they appear in the Solar System as numbers expressing distances of planets that, in their musical counterpart, correspond to the perfect fifth and octave. Hypothetical astronomers on another planet of the Solar System would discover the same Titius-Bode numbers accurately measuring planetary distances, as would astronomers on a planet belonging to another Solar System even if their days were ten times the length of the terrestrial day. They would have to admit that Earthlings have a unique calendar system based upon the rotation of their planet that measures cycles of time in accordance with the
26
proportions of the Solar System. The problem that this poses for Earth astronomers is how people in ancient times could have devised such a calendar if they had no knowledge of the distances between the planets. Uranus, which is not bright enough to be visible to the human eye, was not discovered until 1781 by the astronomer William Herschel. Hard though it may be for astronomers to admit it, such correlation suggests that a source of knowledge existed in ancient times which transcended the limits of the human senses, even when aided by a telescope, and which led to time being measured in units whose duration and numbers could not be arbitrary because they had to harmonize with the cyclic movement of the celestial spheres — in particular, with the Titius-Bode Law.
_________________________
References
1 Phillips, Stephen M. Article 17: “The Logarithmic Spiral Basis of the Titius-Bode Law,” (WEB, PDF), p. 23.
2 A Beginner’s Guide to Constructing the Universe, by Michael Schneider (HarperPerennial, 1994), p. 268.
3 The Occult Power of Numbers, by W. Wynn Westcott (Newcastle Publishing House Co. Inc., North Hollywood, California, 1884), p. 85.
4 All numbers from this table that appear in the text will be written in boldface.
5 Phillips, Stephen M. Article 16: “The Tone Intervals of the Seven Octave Species and Their Correspondence with Octonion Algebra and Superstrings,” (WEB, PDF).
7 Phillips, Stephen M. Article 14: “Why the Ancient Greek Musical Modes are Sacred,” (WEB, PDF).
8 According to the Egyptologist, Moustafa Gadalla, the term for Saturday, the first day of the week in ancient and present-day Egypt, is Sabt. This means Sirius, also known as the Dog Star. It “is referred to as the First, and the D-scale is also referred to as the First scale. All generated music is a variation of this First scale” (Egyptian Rhythm, Moustafa Gadalla (Tehuti Research Foundation, 2002), p. 36).
10 Phillips, Stephen M. Article 18: “Encoding of Planetary Distances and Superstring Structural Parameters in the I Ching Table,” (WEB, PDF).
11 Phillips, Stephen M. Article 15: “The Mathematical Connection between Superstrings and their Micro-psi Description: a Pointer towards M- theory,” (WEB, PDF).
12 Proof: an n-sided, regular polygon with its sectors each divided into three tetractyses has (15n+1) yods, that is, 15n + 1 – (n+1) = 14n yods other than corners of the polygon surround its centre. The sum of the first n odd integers after 1 = (n+1)2 – 1 = n2 + 2n. Therefore, n2 + 2n = 14n, that is, n2 – 12n = 0. Therefore n = 12. This is the dodecagon. With single tetractyses as sectors, an n-sided polygon has (6n+1) yods, that is, 5n yods other than corners surround its centre. Therefore, n2 + 2n = 5n, that is, n2 – 3n = 0, so that n = 3. This is the triangle.
27