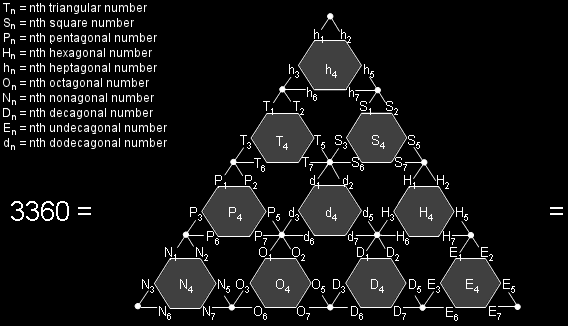
#49 The first 7 orders of the first 10 types of polygonal numbers add up to the number of corners & sides in the 70 polygons of the inner form of 10 Trees of Life

The Nth type of polygonal number of order n is given by:

P^N_n = ½n[(N–2)n – (N–4)].

(P^N₁ = 1 and P^N₂ = N). Here are formulae expressing the first ten types of polygonal numbers: 

Values of the first seven orders of the first ten types of polygonal numbers are tabled below:

s_n is the sum of the first ten types of polygonal numbers for given n:

           12
s_n ≡ Σ P^N_n = 5n(11n−7)/2
            N=3

and ∑_n is the running sum of s_n:

                 n

Σ_n ≡ Σ  s_r = 5n(n+1)(11n−5)/6;
                r=1

As pointed out in comment 8 of the section "Parameters of Superstring & Bosonic String Physics" in Polygonal numbers, the sum ∑₇ of the first seven orders of the first 10 types of polygonal numbers is 3360:

₇

 ∑ (T_n + S_n + P_n + H_n + h_n + O_n + N_n + D_n + E_n + d_n) = 3360.

 ⁿ⁼¹

The number of edges in each half of the 4₂₁ polytope is therefore the sum of 70 polygonal numbers — not a randomly selected set but the first seven orders of the first 10 types of polygonal numbers. Compare this with the following property of the inner Tree of Life: there are two corners and five sides of three triangles per sector of a Type B n-gon, so that the number of corners & sides surrounding the centre of the latter = 7n. Surrounding the centres of the seven separate, Type B polygons are (48×7=336) corners & sides. Surrounding the centres of the 70 separate, Type B polygons making up the inner form of 10 Trees of Life are (336×10=3360) corners & sides:

The first seven orders of the first 10 types of polygonal numbers can be assigned to the seven hexagonal yods in each 1st-order tetractys of the 2nd-order tetractys. It is amazing that the 70 objects in both the 2nd-order tetractys (polygonal numbers) and the inner form of 10 Trees of Life (polygons) generate the same number 3360! It is a powerful testament to the harmony between number and geometry displayed by sacred geometries and physically manifested in the subquark state of the E₈×E₈ heterotic superstring as the 3360 turns in one revolution of its 10 helical whorls, as paranormally described over 100 years ago by Annie Besant and C.W. Leadbeater in their book Occult Chemistry. The 40 red triangles, squares, pentagons & dodecagons are made up of 240 sectors composed of (240×3=720) triangles with (240×7=1680) corners & sides. The 30 blue hexagons, octagons & decagons also have 240 sectors composed of 720 triangles with 1680 corners & sides. The division: 48 = 24 + 24 in the corners of the sets of red and blue polygons per Tree of Life generates the division: 3360 = 1680 + 1680. It manifests in the subquark superstring as the 1680 turns in one half-revolution of its outer or inner halves, each half comprising 2½ revolutions of its 10 whorls.

The largest of the 70 numbers in the first seven orders of the first 10 polygonal numbers is d₇ = 217. This is a structural parameter of the seven enfolded polygons whose 47 sectors are tetractyses, being the number of yods that line the latter:

d7 = 217 =

The (70+70=140) separate Type B polygons of the complete inner form of 10 overlapping Trees of Life have (480+480=960) sectors composed of (960×3=2880) triangles with (3360+3360=6720) corners & sides. This is the number of edges between the 240 vertices of the 4₂₁ polytope. Each half of the inner form of 10 Trees of Life is, as separate polygons, composed of the same number of corners & sides as each half of the 4₂₁ polytope has edges. Can this be nothing more than coincidence? If so, so must be the natural appearance of the number 672 in the first four Platonic solids (see here), the Type C dodecagon (see here), the disdyakis triacontahedron (see here) and the Sri Yantra (see here)! The occurrence of similar, supposed miracles of chance is hard to believe. The evidence that has been accumulated here is unambiguous and irrefutable by such an improbable explanation. The inner form of 10 Trees of Life is analogous to the geometry of the 4₂₁ polytope, two such polytopes representing the roots of E₈×E₈ in the case of Type C polygons (see #47). The only conclusion that can be drawn from this rich encoding is that E₈×E₈ heterotic superstrings are, indeed, part of the cosmic blueprint called the "Tree of Life," with analogous patterns embodying the number 672 being found in other sacred geometries.

Mathematicians or physicists may want to ask: "I would be more impressed if you had shown that the inner form of 10 Trees of Life was composed of 2880 triangles with 6720 sides instead of 6720 corners & sides, because how can points and lines lying in the same plane be equivalent to straight lines joining points distributed in 8-dimensional space, namely, the vertices of the 4₂₁ polytope? The question is misconceived because:

1. by being said to be equivalent, the two systems being compared are meant to be analogous, exhibiting the same pattern of numbers, not to be possessing the same numbers of points, lines or triangles;
2. the fact that two holistic systems display the same global parameter does not mean that this parameter has to quantify the same type of geometrical object. We already know from examples given in the section 4-d sacred geometries and linked to above that this is not the case, so it is unreasonable, as well as misconceived, to expect the inner form of 10 Trees to be composed of 6720 objects of the same type, namely, sides of triangles, as in the case of the 4₂₁ polytope, which has 60480 triangular faces with 6720 edges.

What is crucial to recognise is that, as shown in the linked examples given above and in this section, all sacred geometries embody the number 672 or 6720 as parameters of their global properties. It has emerged in the last few pages that exactly the same parameter is displayed by the inner forms of one Tree of Life and 10 Trees of Life. Why is this? It is not because of some underhand cherry-picking by the author or because a series of highly unlikely coincidences involving at least five different geometrical objects exists but because, being sacred geometry, the patterns and numbers that are characteristic of other sacred geometries exist as well in the inner Tree of Life. Whether sceptics like it or not, it is undeniable that what we have here is an amazing conjunction of advanced mathematics, scientific discoveries in theoretical physics and ancient sacred geometries, all connected by the century-old, paranormal observations of Annie Besant & C.W. Leadbeater, in which the holistic parameter 6720 manifests as the 6720 orthogonal plane waves that make up the 3360 circularly polarised oscillations in one revolution of the 10 whorls of the UPA about its axis of spin.

<< Previous    1...   47  48  [49]  50  51  ...56    Next >>

Home