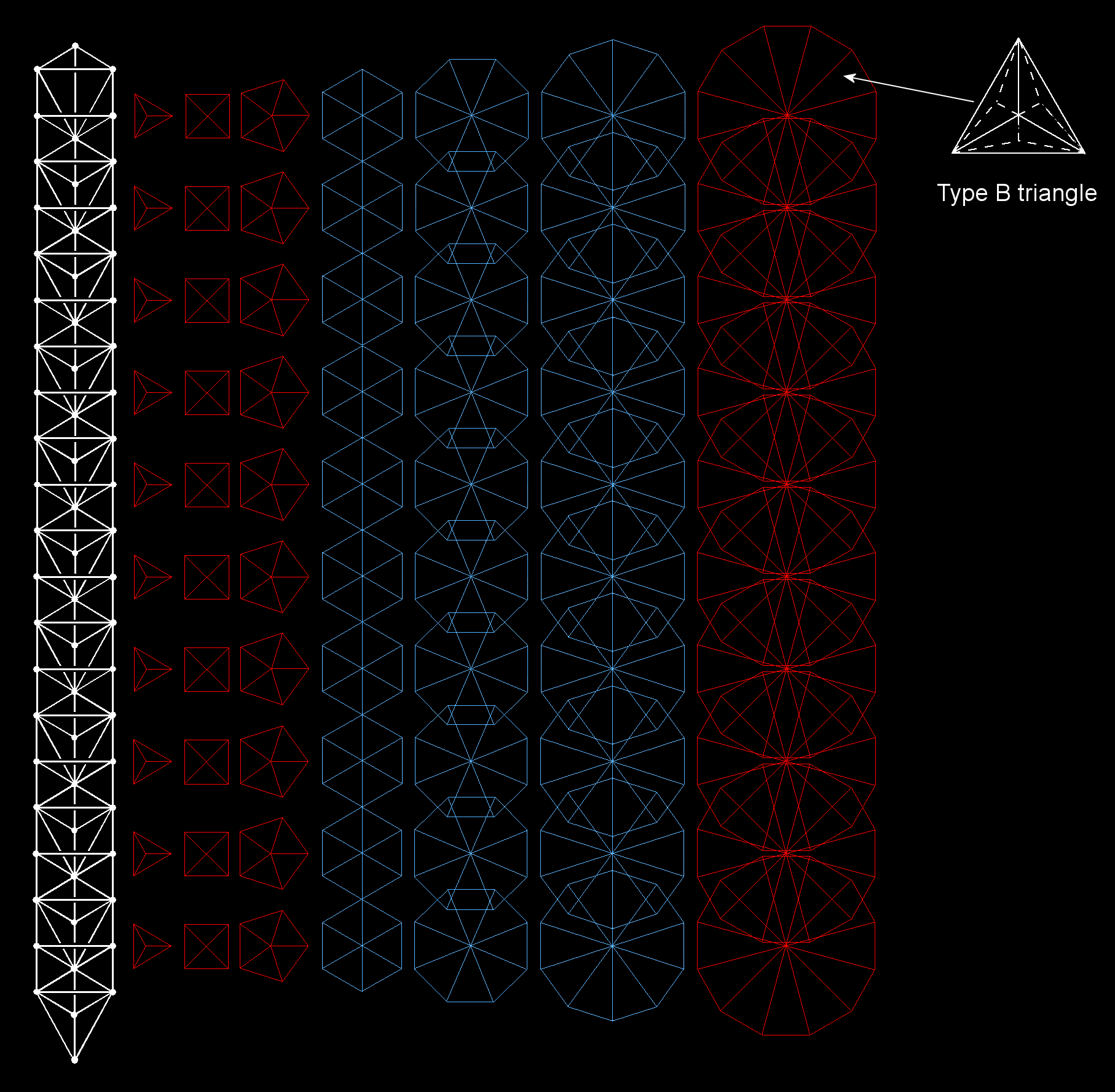
Type B triangle
| << Previous 1... 45 46 [47] 48 49 ...56 Next >> |
#47 Inner form of 10 Trees of Life with Type C polygons is the geometrical counterpart of the two 421 polytopes associated with E8×E8
We found in #46 that the inner form of 10 overlapping Trees of Life, namely, 70 Type B polygons, requires 6720 yods to transform their 480 sectors, each yod corresponding to one of the 6720 edges in the 421 polytope. We now show that, when transformed into Type C polygons, these polygons have (6720+6720) geometrical elements surrounding their centres that correspond to the (6720+6720) edges of the pair of 421 polytopes associated with the symmetry group E8×E8. In other words, the geometrical composition of the inner form of 10 Trees of Life reproduces the number of edges belonging to the two polytopes representing the 480 roots of E8×E8.
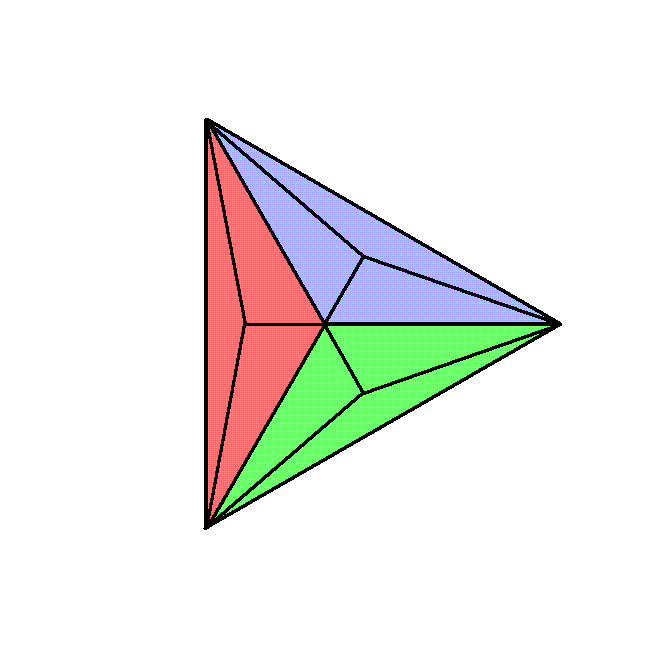
The Type B triangle:
 |
Type B triangle |
has seven corners and 15 sides of 9 triangles, i.e., 31 geometrical elements, where 31 is the number value of EL, the Godname of Chesed. The Type C n-gon has n sectors that are Type B triangles, each sharing one side and two corners with an adjacent sector. This means that the number of geometrical elements in a Type C n-gon = 28n + 1, where "1" denotes its centre. The seven separate Type C polygons making up the inner form of the Tree of Life have 48 sectors with (48×28=1344) geometrical elements surrounding their centres. Curiously, the number 28 also shows up in the representation of 1344 as the sum of squares of four integers, starting with the integer 4:
1344 = 42 + 122 + 202 + 282.
The number 1344 is the arithmetic mean of the squares of the first 31 even integers:
1344 = (22+42+62+...+622)/31.
We saw in #45 that the (7+7) enfolded Type B polygons have (672+672=1344) yods surrounding their centres that are unshared with the outer Tree of Life. That the same number appears again in the next higher-order polygons belonging to both sets of seven polygons cannot, plausibly, be dismissed as chance. The division:
48 = 24 + 24,
which is characteristic of holistic systems, manifests in the 48 corners of the seven separate polygons as the 24 corners of the triangle, square, pentagon & dodecagon and the 24 corners of the hexagon, octagon & decagon. The former set of polygons (coloured red in the diagram below) has (24×28=672) geometrical elements surrounding their centres, as do the latter set (coloured blue).
 |
 |
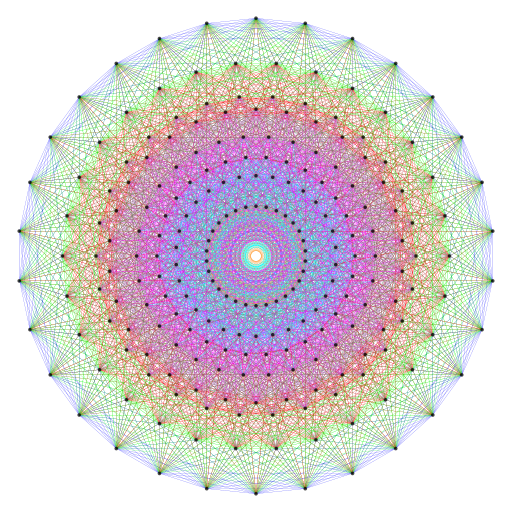
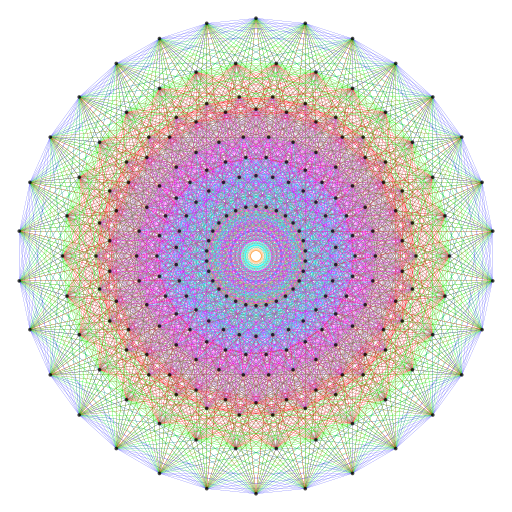
|
Coxeter plane projection of the 421 polytope, |
The 10 sets of Type C triangles, squares, pentagons & dodecagons that are part of the inner form of 10 overlapping Trees of Life have 6720 geometrical elements surrounding their centres, as do the 10 sets of Type C hexagons, octagons & decagons. |
This division, therefore, generates the direct product E8×E8 because the 10 sets of red polygons have 6720 geometrical elements surrounding their centres, as do the 10 sets of blue polygons, so that they correspond to the 6720 edges of the 421 polytope representing each group E8 in the direct product. This is the Tree of Life basis of E8×E8 heterotic superstring theory.
The 28 geometrical elements per Type B sector of the Type C n-gon comprise five corners, 14 sides & nine triangles, i.e., 14 corners & triangles and 14 sides. Hence, the 48 sectors of the seven Type C polygons consist of 672 corners & triangles and 672 sides surrounding their centres, so that the 480 sectors of the 70 Type C polygons in the inner form of 10 Trees of Life comprise 6720 corners & sides and 6720 sides surrounding their centres. We may, alternatively, see the division 13440 = 6720 + 6720 (and, therefore, the direct product E8×E8) as arising from the distinction between the sides and corners & triangles in the polygons. To attribute this, too, to chance is, clearly, implausible in the extreme.
As the last of the regular polygons making up the inner Tree of Life, the Type C dodecagon has 336 geometrical elements (168 corners & triangles, 168 sides) surrounding its centre:
 |
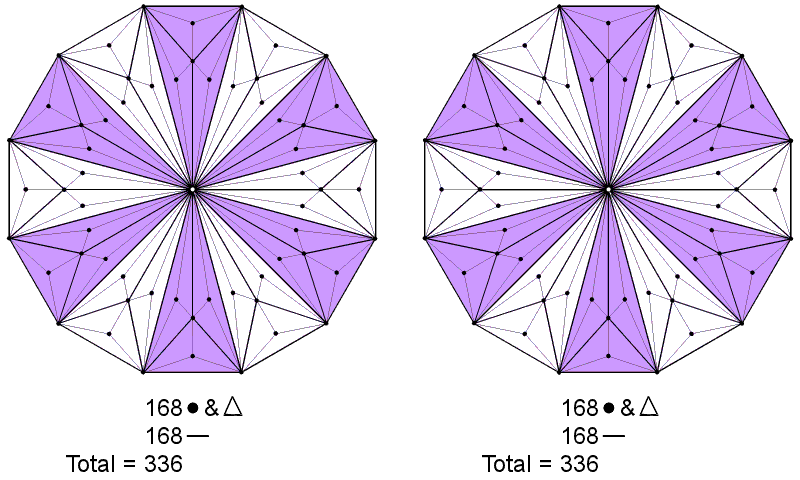 |
|
Each half of the 421 polytope has 3360 edges. |
Constructed from Type B triangles, each of the two Type C dodecagons has 336 corners, sides & triangles surrounding its centre, i.e., 3360 for the 10 dodecagons belonging to the 70 polygons in the inner form of 10 Trees of Life. |
(see also here). The triangle, square & pentagon, too, have 336 geometrical elements surrounding their centres. The 40 triangles, squares, pentagons & dodecagons in the complete set of 70 Type C polygons have 6720 geometrical elements (3360 corners & triangles, 3360 sides) surrounding their centres, as do the 30 hexagons, octagons & decagons. They include the 10 dodecagons with 1680 corners & triangles and 1680 sides. Embodied in the dodecagon is the superstring structural parameter 1680 paranormally obtained by C.W. Leadbeater over a century ago when he applied his micro-psi vision to the UPA. Its identification by the author as the subquark state of the E8×E8 heterotic superstring is confirmed here in the inner Tree of Life basis of the 421 polytope representing the exceptional Lie group E8.
| << Previous 1... 45 46 [47] 48 49 ...56 Next >> |