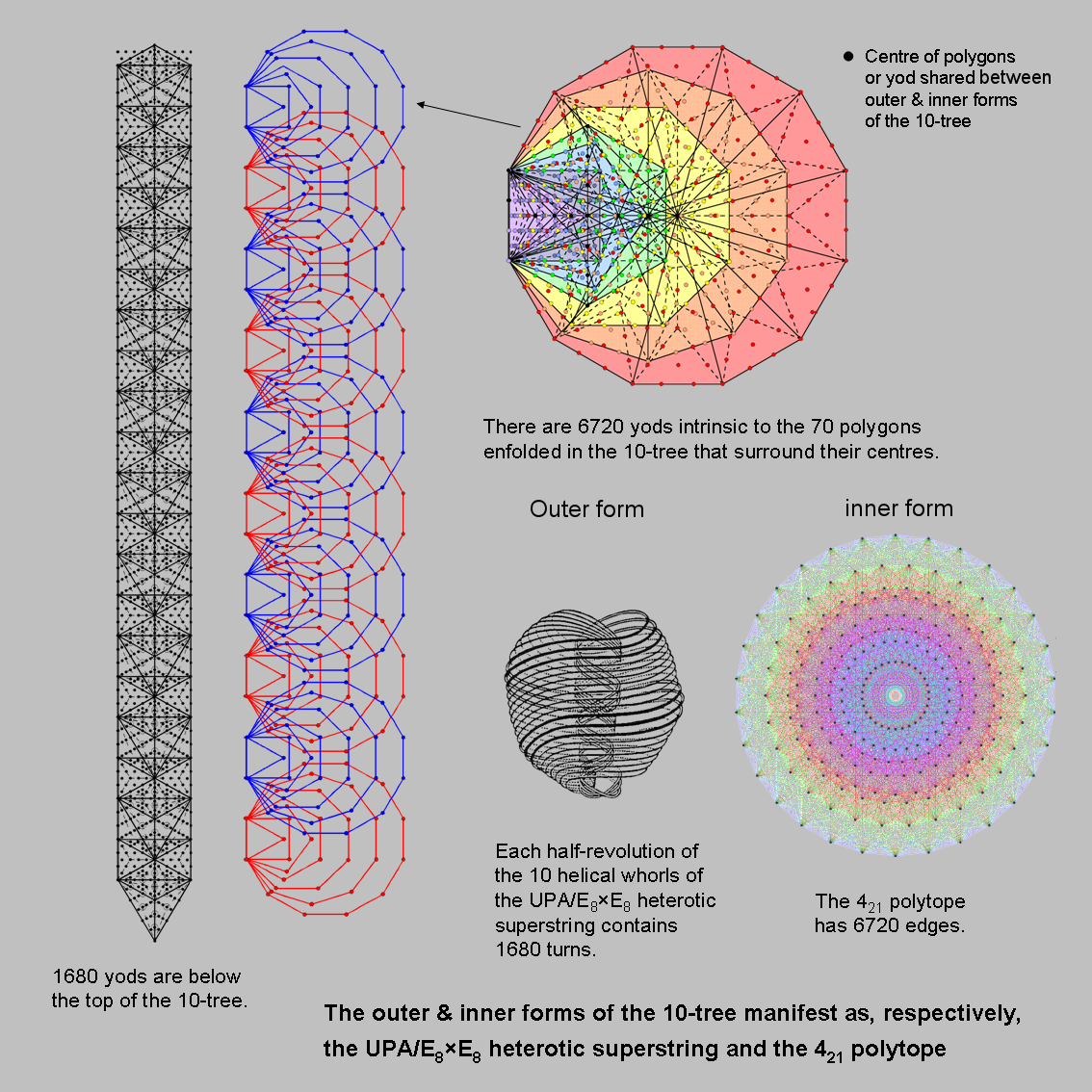
Confirmation that the number (6720) of edges of the 4₂₁ polytope appears in the inner form of 10 overlapping Trees of Life is provided by their yod population. A set of seven enfolded Type B polygons has 687 yods. Seven of these yods (denoted in the diagram above by black yods) are their centres. Another six black yods that line the two vertical sides of sectors of each hexagon are shared with Type A triangles in the outer Tree of Life because they lie on its side pillars. Two yods on the root edge are associated with each set of seven enfolded polygons (the two yods associated with the left-hand set of polygons not shown in the picture are coloured black). This means that the number of yods associated with each set that are unshared with the outer Tree of Life and which surround the centres of the polygons = 687 − 2 − 7 − 6 = 672. The number of such yods in the 70 polygons enfolded on each side of the central Pillar of Equilibrium of 10 overlapping Trees of Life = 10×672 = 6720. Each yod in a polygon surrounding its centre that is intrinsic to the inner form of 10 Trees of Life corresponds to an edge of the 4₂₁ polytope.

Constructed from Type A triangles, the 10-tree has 1680 yods below its apex (for proof, see #2). They denote the 1680 turns in a half-revolution of all 10 helical whorls of the UPA, the subquark state of the E₈×E₈ heterotic superstring. Each yod in the outer form of the lowest 10 Trees of Life denotes one circularly polarized oscillation of a whorl made in a half-revolution of the 10 whorls around the axis of the UPA. Surrounding centres of the (70+70=140) polygons enfolded in the 10-tree are 6720 pairs of corresponding yods that belong solely to them. 140 is the number value of Malachim (or Melekim), the Order of Angels assigned to Tiphareth at the centre of the Tree of Life. There are also 12 black yods per set of seven polygons that are either centres or yods on a side pillar shared with the outer Tree of Life, so that both sets of polygons have (12+12=24) black yods. Hence, there are 240 such yods in the 140 polygons enfolded in the 10-tree that are either shared or centres of polygons. They denote the 240 vertices of the 4₂₁ polytope, the 120 black yods in each set of 70 polygons denoting the 120 vertices in each half of the 4₂₁ polytope, whilst the 6720 unshared yods surrounding their centres correspond to the 6720 hexagonal yods on the 3360 edges in each half of the 4₂₁ polytope when its 60480 triangular faces are turned into tetractyses. As the 240 vertices of this polytope define the 240 root vectors of E₈, here, in the joint appearance of the "mathematical" number 6720 and the paranormally-derived number 1680, is unequivocal evidence that the UPA described by Annie Besant & C.W. Leadbeater is an E₈×E₈ heterotic superstring. The inner form of 10 Trees of Life is simply a planar representation of the 4₂₁ polytope when it is constructed from tetractyses! The 240 yods that are either centres of polygons or shared with the 10 Trees denote its 240 vertices, whilst the 6720 unshared yods surrounding the centres of the 70 polygons in each half of the inner form of 10 Trees denote the 6720 hexagonal yods lining the 3360 edges in each half of the polytope. See also #45.

In conclusion: the following correspondences exist between the inner form of 10 Trees of Life and the 4₂₁ polytope whose faces are tetractyses:

They demonstrate the amazing way in which information embodied in the geometry of the inner form of the Tree of Life is revealed by the tetractys as the template of all sacred geometries. Any suggestion by a sceptic that all four correspondences could arise by chance is ludicrously improbable. The only reasonable conclusion to be draw from these analogous properties is that the 4₂₁ polytope can be said to be the polytopic version of the inner form of 10 Trees of Life. But, as it is the representation of the 240 roots of E₈, which is part of the symmetry group E₈×E₈, one of the two symmetry groups of dimension 496 that are free of quantum anomalies, this can mean only that E₈×E₈ heterotic superstrings really do exist. They are the manifestation in the subatomic world of the Tree of Life blueprint. Its outer form is the superstring itself and its inner form is the 4₂₁ polytope, whose vertices represent the roots of the symmetry group E₈ describing all its forces other than gravity.