#45 The 4₂₁ polytope as the inner form of 10 overlapping Trees of Life

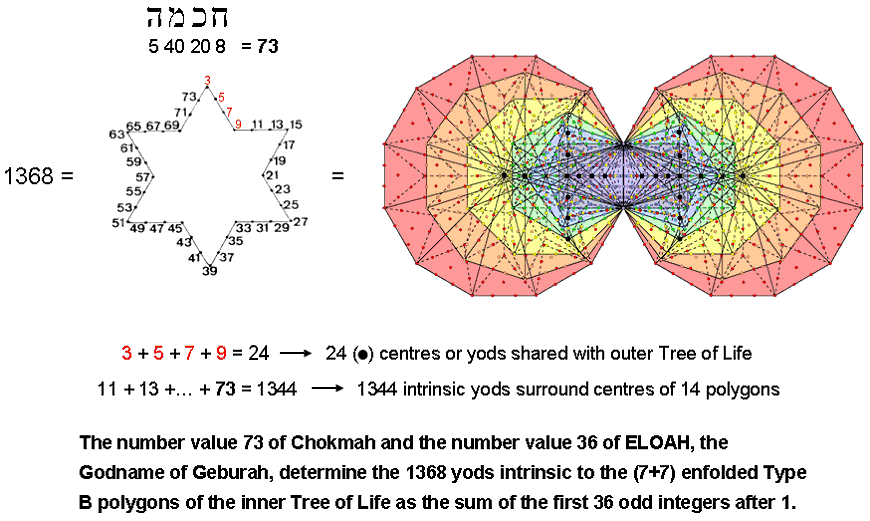
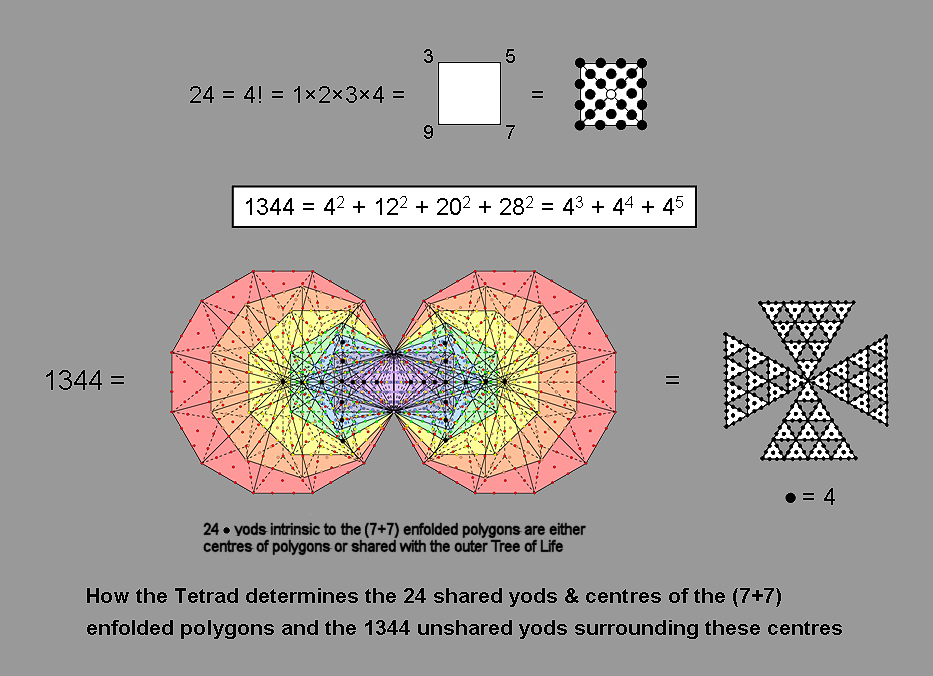
The inner form of the Tree of Life as (7+7) enfolded, Type B regular polygons comprises 1370 yods.* Of these, two yods are the topmost corners of the two hexagons. They coincide with the lowest corners of the hexagons enfolded in the next higher Tree of Life, leaving 1368 yods intrinsic to the set of (7+7) polygons enfolded in each Tree. Seven black yods line the two vertical sides of each hexagon that pass through their centres. One of them is the topmost corner of the hexagon; it is shared with the hexagon enfolded in the adjacent Tree. Six of these yods belong solely to each set of seven enfolded polygons. But they are shared with the outer Tree of Life because they lie on sides of triangles making up the latter. As the outer corner of the triangle is both the centre of the hexagon and one of the six yods, there are six centres and six shared yods (one of which is also a centre of a polygon). Hence, 24 yods are either centres of the (7+7) enfolded polygons or shared with the outer Tree of Life. The number of yods surrounding the centres of the (7+7) enfolded polygons that are not shared with the outer Tree = 1368 − 24 = 1344 = 16×84 = 4²(1²+3²+5²+7²) = 4² + 12² + 20² + 28². As

1368 = 37² − 1 = 3 + 5 + 7 +... + 73

and

 24 = 5² − 1 = 3 + 5 + 7 + 9,

 1344 = 1368 − 24 = 11 + 13 + ... + 73,

i.e., 1368 is the sum of the first 36 odd integers after 1 up to the number 73 of Chokmah that can be assigned to the 36 yods lining the sides of a Star of David (see left-hand picture above), whilst 24 is the sum of the first four odd integers assigned to one side of it, as indicated by the red integers 3, 5, 7 & 9 in the picture. One of the profound meanings of the Star of David is, therefore, that its boundary embodies the very number of yods that are intrinsic to the inner form of the Tree of Life (Otz Chiim).

As

336 = (1²+2²+3²+...+31²)/31,

1344 = 4×336 = 2²×(1²+2²+3²+...+31²)/31 = (2²+4²+6²+...+62²)/31,

i.e., this number is the arithmetic mean of the squares of the first 31 even integers, where 31 is the number value of EL, the Godname of Chesed, and 62 is the number value of Tzadkiel, its Archangel.

Suppose that we now consider 10 overlapping Trees of Life. Its inner form (see right-hand picture) consists of 140 polygons (70 red, 70 blue) with (1368×10=13680) yods belonging solely to these polygons. They contain (24×10=240) yods that are either centres of polygons or shared with outer Trees and (1344×10=13440) unshared yods that surround these centres. Associated with each set of 70 polygons enfolded in 10 Trees are (13440/2=6720) such intrinsic yods surrounding their centres. Each yod in one set of seven polygons can be paired with its counterpart in the other set of seven polygons. This means that there are 6720 pairs of such yods, one yod in each pair being the mirror image of the other.

In mathematics, the polytope is the generalisation of the polygon and the polyhedron. In 1900, Thorold Gosset (1869-1962), an English lawyer and amateur mathematician, discovered an 8‑dimensional, uniform, semi-regular polytope that has proved to be relevant to the theory of superstrings (or at least to the mathematics of one of the two symmetry groups describing superstring forces). Called the "4₂₁ polytope," its 240 vertices coincide with the 240 points in the 8-dimensional space spanned by the 240 vectors representing the roots of the rank-8, exceptional Lie group E₈ that appears in E₈×E₈ heterotic superstring theory. The 4₂₁ polytope has 6720 edges. Constructed from tetractyses, there are 6720 pairs of hexagonal yods on its edges, so that the number of yods lining its edges = 240 + 2×6720 = 13680. But, as we showed above, this is the number of yods in the inner form of 10 overlapping Trees of Life! The following correspondences emerge between the 4₂₁ polytope constructed from tetractyses and the inner form of 10 Trees of Life:

Why does this amazing parallelism exist? Certainly, it is too detailed to have arisen by chance. That is not plausible. No, the parallelism exists simply because the 4₂₁ polytope is a holistic object that possesses the universal sacred geometry of such objects. It is the 8-dimensional, polytope counterpart of the disdyakis triacontahedron in 3-dimensional space (see #18 in 4-d sacred geometries). Constructed from tetractyses, the two halves of the 4₂₁ polytope, each with 3360 edges, lining which are 120 vertices and 6720 hexagonal yods, correspond in the inner form of 10 Trees to its two sets of 70 enfolded polygons, each set having 120 centres or yods shared with Trees and 6720 unshared yods that surround the centres of these polygons.

Does the 4₂₁ polytope possess a 10-fold division, just as its counterpart as the inner form of 10 Trees of Life has? Certainly, it does for its 240 vertices. Their projection into 4-dimensional space is known to be a compound of two 600-cells, one smaller than the other, sharing the same centre. Each 600-cell is known to be a compound of five 24-cells, so that the 4-dimensional projection of the 240 vertices of the 4₂₁ polytope defines the 240 vertices of 10 24-cells, i.e., 10 sets of 24 vertices. Amazingly, when the 24-cell is constructed from Type A triangles, there are 672 corners, sides & triangles other than vertices & edges in its faces, its construction needing a total of 1368 extra corners, sides & triangles (see here). As

672 = 4×168 = 2²×(13²−1) = 26² − 2² = (1+3+5+...+51) − (1+3) = 5 + 7 + 9 +....+ 51,

this number is the sum of 24 (=1×2×3×4) consecutive odd integers, starting with 5, the fourth integer after 1. So the Tetrad determines both the number of vertices in the 24-cell and the extra number of geometrical elements needed to construct its faces. The 10 24-cells comprise 6720 geometrical elements in their faces other than vertices & edges, their construction requiring in total 13680 extra geometrical elements, of which 240 are internal sides of triangles extending from their vertices to the centres of 24-cells. Exactly the same holistic parameters of the 4₂₁ polytope — 240, 6720 & 13680 — appear in the 10 24-cells as they do in both the inner form of 10 Trees of Life and the yods on the edges of the 4₂₁ polytope constructed from tetractyses! The inner form of each Tree of Life can be interpreted in this context as representing a 24-cell, the 1368 yods in the former symbolising the 1368 geometrical elements making up the 24-cell. Such astounding correlations between the inner form of 10 overlapping Trees of Life, the 4₂₁ polytope and the 10 24-cells in the compound of two 600-cells provide powerful evidence for the 4₂₁ polytope being the 8-dimensional, polytopic version of this inner form. What, then, does the outer form of 10 Trees signify? None other than the UPA, each Tree representing one of the 10 half-revolutions of its 10 whorls. Spread along each of these half-revolutions are 24 gauge charges of E₈ whose associated root vectors, projected into 4-dimensional space, define the 24 vertices of a 24-cell, whose 1368 geometrical elements are symbolised by the 1368 yods making up the inner form of each overlapping Tree of Life.

Shown below is how the Pythagorean Tetrad determines the numbers 24 and 1344 through the square and the cross pattée with 2nd-order tetractyses as its arms.

For a more detailed discussion, see under the heading "The 4₂₁ polytope" on #2 in 4-d sacred geometries. See also Article 63: "The sacred geometrical nature of the 4₂₁ polytope."

* Proof: Each set of 7 enfolded, Type B polygons has 47 sectors with 41 corners, 42 polygonal sides, 46 internal sides and 10 internal yods in each sector. Number of yods in 7 enfolded, Type B polygons = 41 + 42×2 + 46×2 + 47×10 = 687 (683 outside their root edge). Number of yods in (7+7) enfolded, Type B polygons = 4 + 683×2 = 1370.

<< Previous    1...   43  44  [45]  46  47  ...56    Next >>

Home