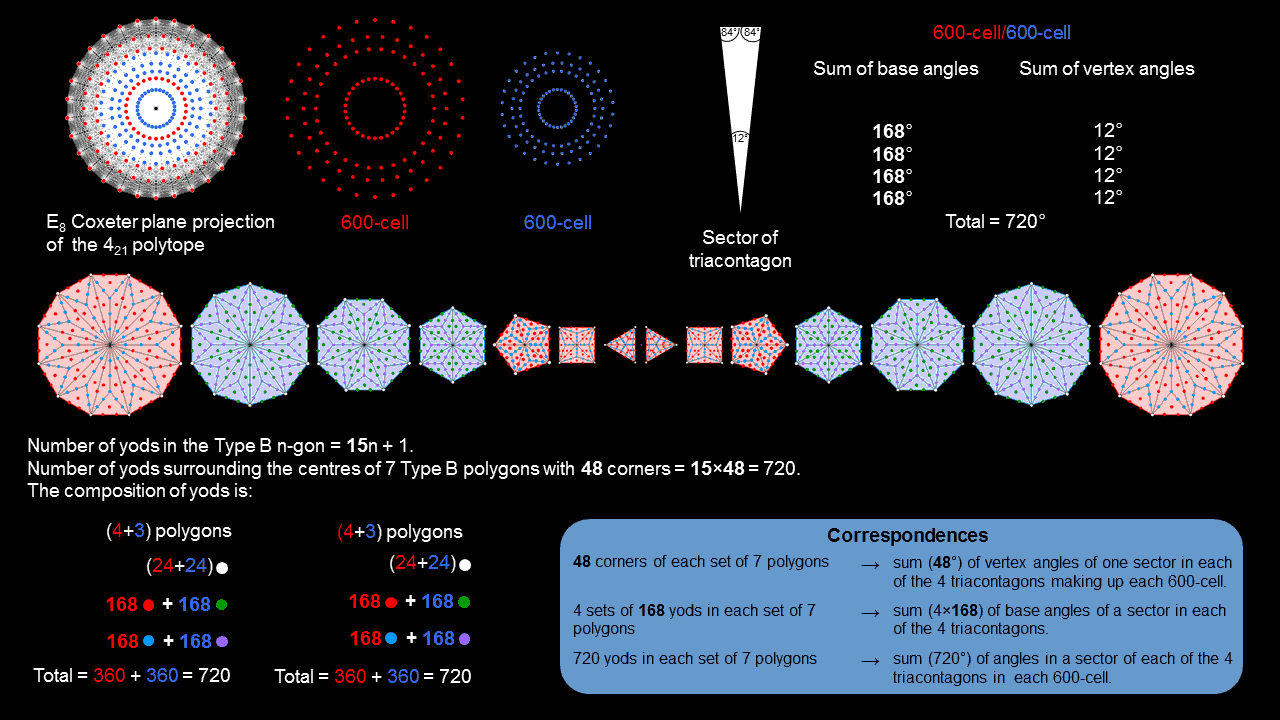
The yod population of the (7+7) Type B polygons matches the sum of interior & vertex angles of a sector in the 8 triacontagons in the E8 Coxeter projection of the 421 polytope.
| << Previous 1... 3 4 [5] 6 7 ...17 Next >> |
5. The pattern of interior & vertex angles in 8 sectors of the 8 triacontagons matches the yod population of the (7+7) Type B polygons
 |
The yod population of the (7+7) Type B polygons matches the sum of interior & vertex angles of a sector in the 8 triacontagons in the E8 Coxeter projection of the 421 polytope. |
The 8 triacontagons in the E8 Coxeter plane projection of the 421 polytope consist of two sets of 4 (shown coloured red & blue). Each set of 120 vertices is the Coxeter plane projection of a 600-cell. If we consider a representative sector in each triacontagon, the sum of the base angles in either set =4×168 = 672° and the sum of the vertex angles = 4×12 = 48°. The sum of the angles of a sector in each set = 720°. The sum of the angles of the 8 representative sectors = 720° + 720° = 1440° = 48° + 672° + 48° + 672°. Compare this with the yod population of the (7+7) separate Type B polygon: Surrounding the centre of a Type B n-gon are 15n yods. Surrounding the centres of each set of 7 Type B polygons are 48 corners and (48×14=672) yods, i.e., 720 yods in all. The correspondence indicates that a yod denotes a single degree; the 48 corners of each set of polygons denote the 48 degrees in the sum of the vertex angles of the 4 representative sectors in each set of 4 triacontagons, whilst the 672 yods denote the sum of their base angles. The red triangle, square, pentagon & dodecagon have 24 corners and 336 other yods, as do the blue hexagon, octagon & decagon. The 360 yods in each subset of polygons symbolise the 360 degrees of a circle, corresponding to two sectors. One set of 7 polygons corresponds to the representative sectors in one set of 4 triacontagons associated with one 600-cell and the other set corresponds to the second 600-cell. In terms of angles, the two halves express revolutions of (2+2) full circles.
| << Previous 1... 3 4 [5] 6 7 ...17 Next >> |