Home

4. The triacontagon has the holistic pattern of the Type B dodecagon & the disdyakis triacontahedron

The 12:84:84 pattern in the Type B dodecagon and the disdyakis triacontahedron.

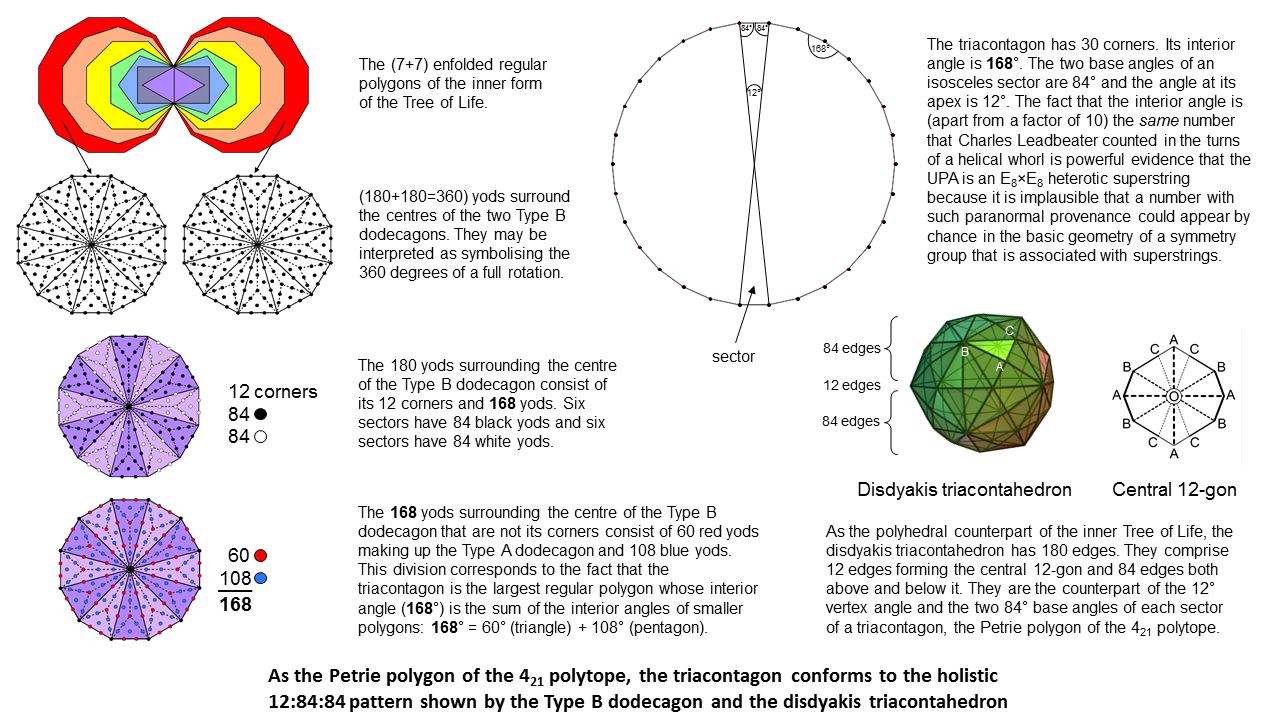
The dodecagon is the last of the seven types of regular polygons making up the inner form of the Tree of Life. 180 yods surround its centre when it is Type B. The 360 yods surrounding the centres of the two Type B dodecagons in the (7+7) regular polygons symbolise the 360 degrees in a circle, so that each dodecagon represents a half-revolution of 180°. Its 12 corners denote the 12 degrees in each sector of the triacontagon. The 168 other yods surrounding its centre denote the 168 degrees in the two base angles of a sector. The 6 corners & 84 yods in the pair of 6 sectors of the Type B dodecagon denote the angles of 6° & 84° in the pair of right-angled triangles making up a sector of the triacontagon. Of the 168 yods, 60 belong to the Type A dodecagon as yods other than its corners, leaving 108 yods. The interior angles of an equilateral triangle and a pentagon are, respectively, 60° and 108°. The significance of these polygons is that the triacontagon is the largest regular polygon whose interior angle is the sum of the interior angles of smaller polygons, namely, the triangle and the pentagon.

The disdyakis triacontahedron has 62 vertices: 30 A, 12 B & 20 C vertices. When orientated so that its vertical axis passes through two diametrically opposite A vertices, a 12-gon whose corners coincide with 4 A, 4 B & 4 C vertices lies in its equatorial plane. All its sides are edges of the polyhedron. The 180 edges of the disdyakis triacontahedron comprise the 12 edges forming the central 12-gon and 168 edges, arranged as 84 edges either above or below it. This 84:12:84 division of edges corresponds to the three angles of a sector of the triacontagon, the Petrie polygon of the 4₂₁ polytope. It is additional evidence for the holistic character of the 4₂₁ polytope and therefore the reality of E₈×E₈ heterotic superstrings. 

<< Previous    1...   2  3  [4]  5  6  ...17    Next >>

Home