| << Previous 1... 34 35 [36] 37 38 ...45 Next >> |
The seven species of musical octaves comprise 14 different notes. In order of increasing tone ratios, they are:
|
1 |
256/243 |
9/8 |
32/27 |
81/64 |
4/3 |
1024/729 |
729/512 |
3/2 |
128/81 |
27/16 |
16/9 |
243/128 |
2 |
(black numbers denote notes belonging to the Pythagorean scale and red numbers denote non-Pythagorean notes). Their musical names are listed below:
| Note | Tone ratio |
Size (cents) |
|
|
Pythagorean tuning |
Equal-tempered tuning | ||
| Unison |
1/1 |
0.00 |
0 |
|
Minor second |
256/243 |
90.22 |
100 |
|
Major second |
9/8 |
203.91 |
200 |
|
Minor third |
32/27 |
294.13 |
300 |
|
Major third |
81/64 |
407.82 |
400 |
|
Perfect fourth |
4/3 |
498.04 |
500 |
|
Diminished fifth |
1024/729 |
588.27 |
600 (tritone) |
|
Augmented fourth |
729/512 |
611.73 |
|
|
Perfect fifth |
3/2 |
701.96 |
700 |
|
Minor sixth |
128/81 |
792.18 |
800 |
|
Major sixth |
27/16 |
905.87 |
900 |
|
Minor seventh |
16/9 |
996.09 |
1000 |
|
Major seventh |
243/128 |
1109.78 |
1100 |
|
Octave |
2/1 |
1200.00 | 1200 |
They form seven pairs of notes X and their inversions Y, where XY = 2:
|
X |
Y |
XY |
||||
|
1. |
1/1 |
2 |
T5L2 |
1×2 |
= 2 |
|
|
2. |
L |
256/243 |
243/128 |
T5L |
256/243×243/128 |
= 2 |
|
3. |
T |
9/8 |
16/9 |
T4L2 |
9/8×16/9 |
= 2 |
|
4. |
TL |
32/27 |
27/16 |
T4L |
32/27×27/16 |
= 2 |
|
5. |
T2 |
81/64 |
128/81 |
T3L2 |
81/64×128/81 |
= 2 |
|
6. |
T2L |
4/3 |
3/2 |
T3L |
4/3×3/2 |
= 2 |
|
7. |
T2L2 |
1024/729 |
729/512 |
T3 |
1024/729×729/512 |
= 2 |
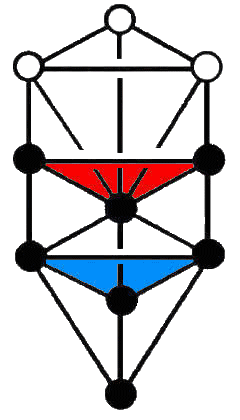
T = 9/8 is the Pythagorean tone interval & L = 256/243 is the Pythagorean leimma (from the Greek word for "leftover", this being the interval between the penultimate note of the Pythagorean octave with tone ratio 243/128 and the first note of the next octave with tone ratio 2. The 12 notes between the tonic & octave comprise a triplet of Pythagorean notes, a triplet of non-Pythagorean notes and the two triplets of their corresponding inversions. This (1,3,3) pattern of a set of seven notes and their seven inversions is fundamental to holistic systems because it is the manifestation in them of the seven archetypal creative, divine principles called the Sephiroth of Construction, which form two triads and a single Sephirah, Malkuth, at the foot of the Tree of Life:

Chesed-Geburah-Tiphareth
Netzach-Hod-Yesod
Malkuth
The counterpart of this (1,3,3) pattern in the tetractys is its central hexagonal yod and the two triangular arrays of hexagonal yods that intersect to form a Star of David/Sign of Vishnu (see here). Other examples of the double 7-fold pattern & 1:3:3 divisions characteristic of holistic systems are discussed below.
Inner Tree of Life
The inner form of the Tree of Life consists of two
sets of seven regular polygons, one set being the mirror image of the other. Each set comprises the
dodecagon, the set of triangle, square & pentagon (i.e., three polygons) and the set of hexagon,
octagon & decagon (i.e., three polygons):
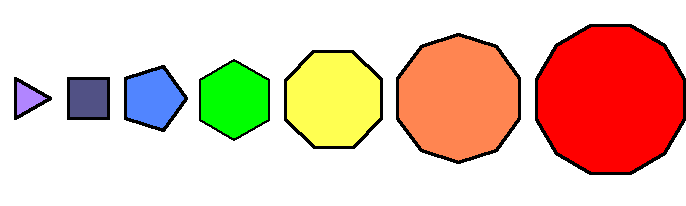 |
The 7 polygons of the inner Tree of Life |
The seven polygons have 48 corners: 12 corners of the dodecagon, 12 corners of the triangle, square & pentagon and 24 corners of the hexagon, octagon & decagon. The 1:3:3 pattern characteristic of holistic systems naturally generates the 24:24 division of the number 48 that is always characteristic of sacred geometries (see here).
Musical scales
The 1:3:3 pattern manifests in the seven musical
scales as the D scale (Dorian mode), whose pattern of intervals between successive notes is unique
among these scales because it is its own mirror image:
T L T T T L T ↔ T L T T T L T
and as two sets of three scales: three authentic modes (E, F & G scales) and three plagal modes (C, B & A scales), the members of the former having patterns of intervals that are mirror images of the patterns in corresponding members of the latter:
|
Authentic modes |
Plagal modes |
|||||
|
Phrygian |
= | LTTTLTT | ↔ | TTLTTTL | = | Hypolydian |
|
Lydian |
= | TTTLTTL | ↔ | LTTLTTT | = | Hypophrygian |
|
Mixolydian |
= | TTLTTLT | ↔ | TLTTLTT | = | Hypodorian |
The 1:3:3 pattern also appears in the first seven notes in the basic set of 14 notes and in their inversions, for the former consists of the tonic, a triplet of Pythagorean notes & a triplet of non-Pythagorean notes, whilst the latter comprises the octave, a triplet of Pythagorean notes & a triplet of non-Pythagorean notes. The double 7-fold pattern in the seven scales is of (7×27=189) rising intervals below the octave between their notes and their corresponding 189 falling intervals. This pattern appears in the 8×8 square array of 64 hexagrams of the I Ching as the seven copies in its upper diagonal half of the eight upper triagrams in its diagonal and as the seven copies in its lower diagonal half of the eight lower trigrams in its diagonal.
Disdyakis triacontahedron
The 60 vertices that surround an axis passing through
two opposite vertices of this polyhedron are arranged in seven layers if the two vertices are A vertices and in
15 layers if they are C vertices (see here). In the former case, below the top A vertex is a 8-gon, a
10-gon & a 6-gon, then a central 12-gon, followed by the inversions of the upper triplet of polygons. In the
latter case, the seven polygons either above or below the central 6-gon consist of two triplets of polygons (two
3-gons & a 6-gon), and a 3-gon, respectively, above or below a C vertex. In either case, the seven polygons
comprise a central polygon and two triplets of polygons, i.e., they form a 1:3:3 pattern.
Sri
Yantra
The last layer of 14 triangles consists of two sets of seven triangles, one the mirror image of the other reflected
across the horizontal axis. The upper seven triangles comprise an uppermost black triangle that is the apex of the
largest, upward-pointing Shiva triangle, three red triangles and their blue mirror images reflected across the
vertical axis that are apices of three downward-pointing Shakti triangles. The seven lower triangles
comprise a lowest white triangle that is the apex of the largest, downward-pointing

Shakti triangle, three pink triangles and their cyan mirror images reflected across the vertical axis that are apices of three upward-pointing Shiva triangles. This means that the 'polarities' of the triangles, defined in terms of the parent Shiva (positive) and Shakti (negative) triangles are:
|
7 Upper triangles |
7 Lower triangles |
|
|
+, (−,−,−) & its mirror image (−,−,−) |
−, (+,+,+) & its mirror image (+,+,+) |
Each set of seven triangles consists of a singlet and two triplets. Each set is the polar opposite of the other set, as are the two singlets (black & white triangles).
The apices of six triangles touch the circumscribing circle with eight lotus petals (see here). This 8:6 differentiation in the 14 triangles has its musical counterpart in the eight Pythagorean notes and six non-Pythagorean notes that make up the seven musical scales (see beginning of page). In fact, the first seven notes consist of the tonic, three Pythagorean notes & three non-Pythagorean notes, and their inversions in the second set consist of three Pythagorean notes, three non-Pythagorean notes & the octave. The two triplets of triangles in one half correspond to the triplet of Pythagorean notes and the triplet of non-Pythagorean notes, whilst the two triplets in the other half correspond to the three Pythagorean & three non-Pythagorean notes that are the inversions of the former, with the black triangle corresponding to the tonic and the white triangle corresponding to the octave.
| << Previous 1... 34 35 [36] 37 38 ...45 Next >> |