| << Previous 1... 35 36 [37] 38 39 ...45 Next >> |

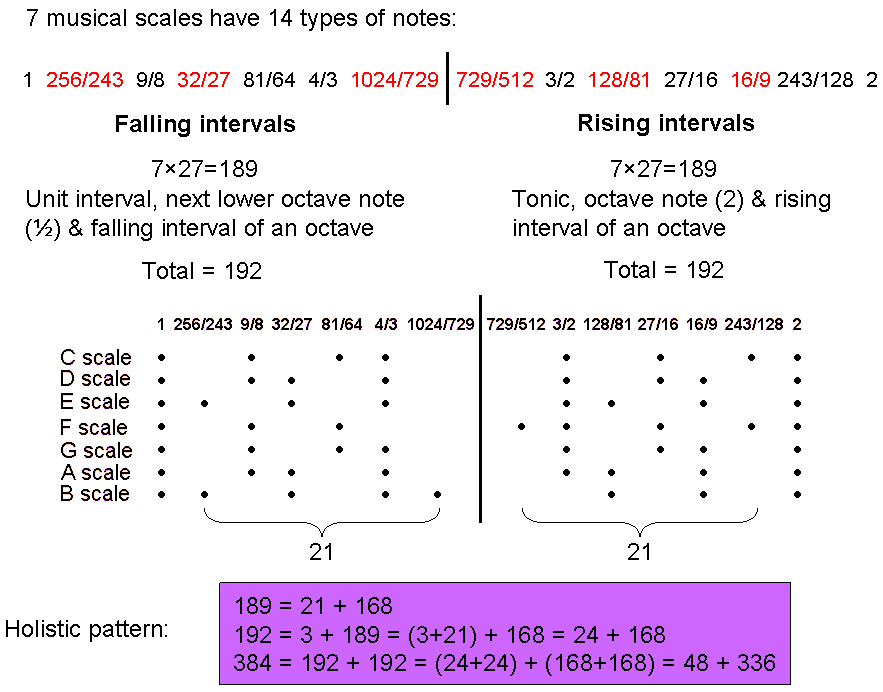
Each of the seven scales has 27 intervals below the octave. The (7×27=189) intervals include the 42 notes between the tonic and octave. Inspection of the table above shows that there are 21 notes and their 21 inversions. The Godname EHYEH with number value 21 prescribes each set because its letter values denote subsets of notes and their inversions:
|
AHIH = 21 |
|
| A = 1 → 1×(1024/729) | → 1×(729/512) |
| H = 5 → 5×(9/8) | → 5×(16/9) |
| I = 10 → 4×(32/27) + 6×(4/3) | → 4×(27/16) + 6×(3/2) |
| H = 5 → 2×(256/243) + 3×(81/64) | → 2×(243/128) + 3×(128/81) |
Just as a note is paired
with its inversion, so any interval can be paired with its inversion. However, unlike notes, there is not the same
number of intervals and their inversions. The table lists these numbers. There are 125 intervals but
64 inversions. The table shown below lists the numbers of notes, intervals and their
inversions that can be paired, as well as the numbers of unpaired intervals and their inversions (black tone ratios
are Pythagorean, red tone ratios are non-Pythagorean). There are 63 notes & intervals that can be paired with
their inversions and 63 other intervals that cannot be paired (see the last row in the table). Hence, the 189
intervals below the octave split naturally into three sets of 63: 1. 63 notes & intervals; 2.
their 63 inversions, and 3. 63 intervals without their accompanying inversions.

Notice that they consist of 21 notes and 168 inversions & intervals (see bottom of table). 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, and the superstring structural parameter that is embodied in sacred geometries (see Superstrings as sacred geometry). It does not appear in this context by coincidence. Instead, the 21:168 division is characteristic of such geometries and holistic systems like the seven musical scales. As confirmation that chance is not involved here, notice that the 168 inversions & intervals consist of 42 pairs of intervals & their inversions, i.e., 84 intervals, and 84 inversions & unpaired intervals (21 paired inversions, 62 unpaired intervals & one unpaired inversion). This 84:84 division is another pattern found in holistic systems. For example, it occurs in the (6+6) enfolded polygons as the 84 yods lining the edges of each set of six polygons outside their shared edge (see here). It also occurs in the first four Platonic solids as the 84 yods needed on average to build each half of them from tetractyses (see here).
| << Previous 1... 35 36 [37] 38 39 ...45 Next >> |