| << Previous [1] 2 3 Next >> |
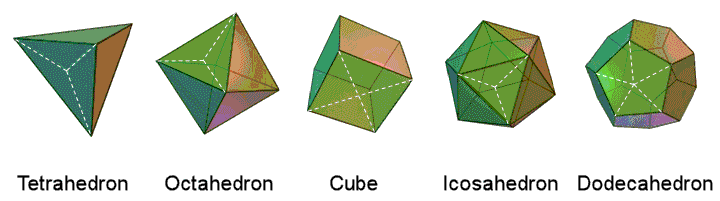
The Platonic solids

The five Platonic solids
The tetrahedron, octahedron and icosahedron have triangular faces, the cube has square faces and the dodecahedron has pentagonal faces. Consider each face of a Platonic solid divided into its sectors. The table below lists their numbers of corners, sides & triangular sectors.
Number of vertices = V; number of edges = E; number of faces = F; number of sectors in a face = m.
Number of corners = C = V + F; number of sides = e = E + mF; number of triangles = T = mF (m = 3 for tetrahedron, octahedron & icosahedron; m = 4 for cube; m = 5 for dodecahedron).
Geometrical composition of the five Platonic solids
|
Polyhedron |
V |
E |
F |
m |
C |
e |
T |
Total = C + e + T |
|
tetrahedron |
4 |
6 |
4 |
3 |
8 |
18 |
12 |
38 |
|
octahedron |
6 |
12 |
8 |
3 |
14 |
36 |
24 |
74 |
|
cube |
8 |
12 |
6 |
4 |
14 |
36 |
24 |
74 |
|
icosahedron |
12 |
30 |
20 |
3 |
32 |
90 |
60 |
182 |
|
Subtotal |
30 |
60 |
38 |
- |
68 |
180 |
120 |
368 |
|
dodecahedron |
20 |
30 |
12 |
5 |
32 |
90 |
60 |
182 |
|
Total |
50 |
90 |
50 |
- |
100 |
270 |
180 |
550 |
Embodiment of the holistic parameter 550
a) Geometry of faces
The lowest row in the table indicates that there are 550 corners, sides & triangles in the
50 faces of the five Platonic solids. The Divine Name ELOHIM with number value
50 that is associated with Binah, the third Sephirah in the Tree of Life, prescribes the five
regular polyhedra with 50 vertices and 500 (=50×10) other geometrical
elements. This demonstrates par excellence the formative, or shape-determining, nature of the
archetypes embodied in this Sephirah heading the Pillar of Judgement (one of the Kabbalistic titles of Binah is
"Aima," the divine mother). The shapes of the regular polyhedra require 550 geometrical elements to create them,
where 550 = 10(1+2+3+4+5+6+7+8+9+10) = 10(12+22+32+42+52),
i.e., this number is the sum of 50 squares of integers. They include 100 corners of 180
triangles, where 100 (the 50th even integer) = 102 = 13 +
23 + 33 + 43. This illustrates how the Pythagorean Decad (10=1+2+3+4)
and the integers 1, 2, 3 & 4 symbolized by the four rows of dots in the tetractys symbolizing the Decad express
the geometry of the Platonic solids. Their holistic character is demonstrated by the fact that their faces are
composed of 550 geometrical elements, for this is the number of SLs in the 91 Trees of Life that make up
CTOL:
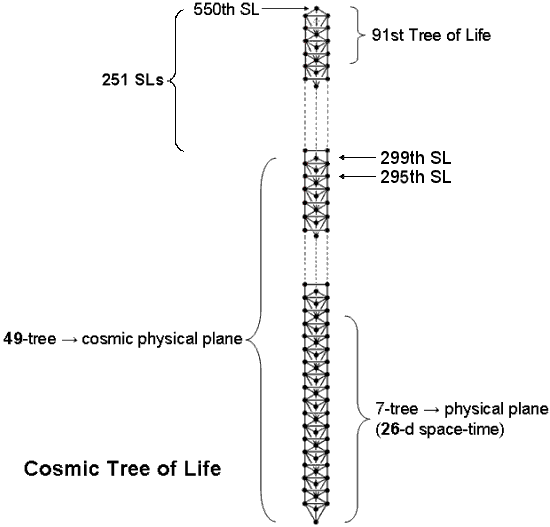
(SL = Sephirothic level, denoted by the black dots in the diagram above). Every single, geometrical element composing the faces of the five Platonic solids corresponds to an SL of CTOL. Notice also that 550 = 10×55, where 55 is the tenth number after the beginning of the famous Fibonacci sequence of numbers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, .....
550 is, therefore, not only ten times the sum of the first ten integers after 0 but also ten times the tenth Fibonacci number after 0! This beautiful property points to a deep involvement of the Fibonacci numbers in the sacred geometry of the Platonic solids. This is confirmed in Article 50 (Parts 1 & 2) (WEB, PDF). As 550 = 10 + 20 + 30 + 40 + 50 + 60 + 70 + 80 + 90 + 100, the tetractys array of the first ten integers multiplied by 10:
|
10 |
10 |
||||||||||||
| 20 | 30 | 20 | 30 | ||||||||||
| 40 |
50 |
60 |
= | + |
40 |
50 |
60 |
= |
180 + 50 + (20+30=50) + (40+60+80+90=270), | ||||
|
70 |
80 | 90 | 100 | 70 | 100 | 80 | 90 |
naturally reproduces the geometrical composition of the triangles making up the five Platonic solids! This is because:
The 550 geometrical elements making up the faces of the five Platonic solids consist of their 50 vertices and 500 other elements. This 50:500 division manifests in the superposed outer and inner Tree of Life as the 50 intrinsic yods other than Sephiroth that belong solely to the former and as the 500 yods belonging only to the (7+7) enfolded polygons that surround their centres (see here). The 50 vertices of the five Platonic solids correspond to the outer Tree of Life with 50 intrinsic yods and the 500 extra geometrical elements needed to construct the faces of the Platonic solids correspond to the inner Tree of Life with 500 intrinsic yods. Four of these extra elements are the centres of the faces of the tetrahedron. They correspond to the four yods on the root edge shared by the (7+7) enfolded polygons.
 |
|
|
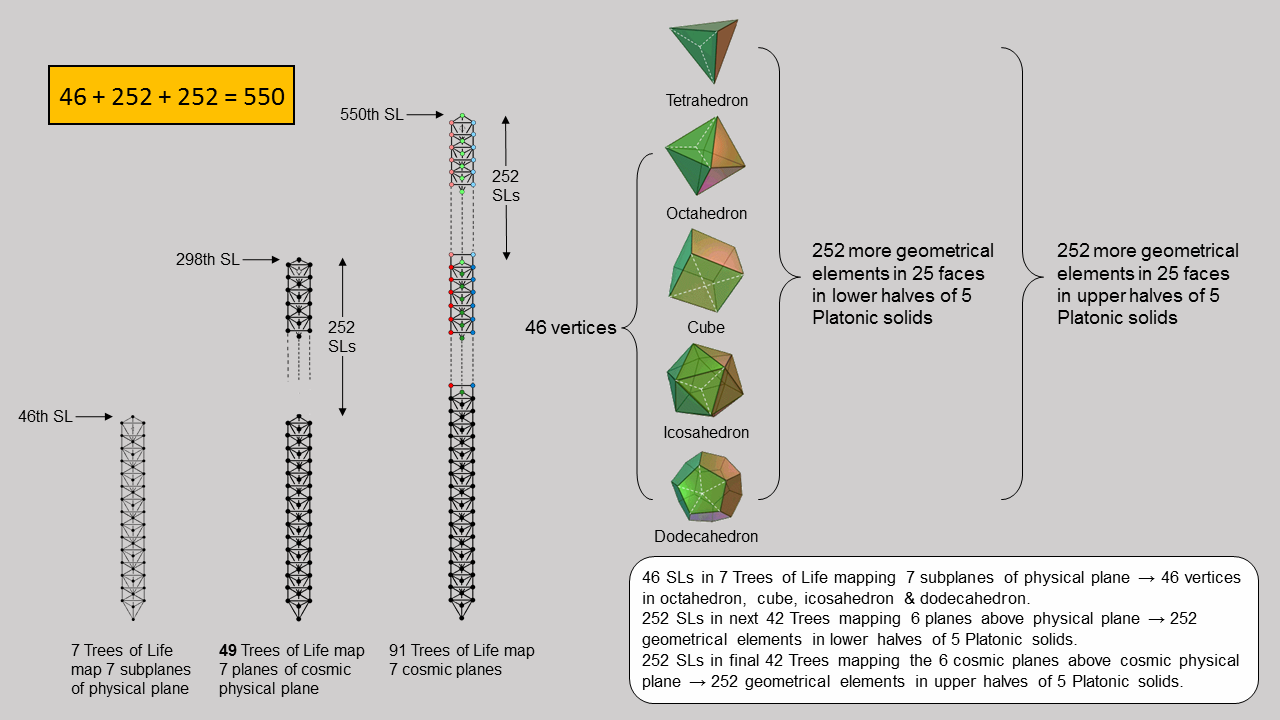
The picture above shows how the 550 geometrical elements correspond to the 550 SLs in CTOL. Seven overlapping Trees of Life have 46 SLs. This is also the number of SLs below the top of the seventh Tree of Life in CTOL. They correspond to the 46 vertices of all the Platonic solids except the tetrahedron. The remaining 504 geometrical elements comprise 252 more elements in the lower halves of the five Platonic solids and 252 elements in their upper halves. The former correspond to the 252 SLs in the next 42 Trees up to the top (298th SL) of the highest Tree in 49 overlapping Trees of Life; counting the top of the 7-tree, there are 252 SLs up to the top of the 49-tree. The latter correspond to the 252 SLs in the next 42 Trees up to the top (550th SL) of the 91st Tree. The upper halves (excluding vertices) correspond to the six cosmic superphysical planes with 42 subplanes mapped by 42 Trees, whilst the lower halves (again, excluding vertices) correspond to the six superphysical planes with 42 subplanes mapped by 42 Trees. The 46 vertices correspond to the 46 SLs of seven Trees mapping the physical plane. As will be revealed in the discussion of the Sri Yantra in the next section, this 46:252:252 division exists as well in the representation of the seven cosmic planes/CTOL by the Sri Yantra.
b) Yod composition of tetractys sectors of faces
When the mF sectors of the faces of a Platonic solid with (E+mF) sides become tetractyses, they have [2(E+mF) = 2E
+ 2mF] hexagonal yods on their sides and (V + F = 2 + E) corners, using Euler's formula for a convex
polyhedron:
V − E + F = 2.
Therefore, the number of yods lining the sides of the mF tetractyses in the faces of a Platonic solid = 2E + 2mF + 2 + E = 2 + 3E + 2mF. "2" denotes two diametrically vertices (two adjacent vertices, in the case of the tetrahedron). For the five Platonic solids, ∑E = 90 and ∑mF = 180 (see table above). The number of yods lining the sides of the 180 tetractyses in the 50 faces of the five Platonic solids = ∑(2+3E+2mF) = 5×2 + 3×90 + 2×180 = 640, where 640 is the number value of Shemesh, the Mundane Chakra of Tiphareth. They include 50 vertices and 50 corners of sectors at the centres of their faces. Hence, (640−50−50=540) hexagonal yods line the sides of their 180 tetractyses. (10+540=550) yods line these sides other than the 40 vertices and the centres of the 50 faces that surround axes passing through the two diametrically opposite vertices of each Platonic solid (any two adjacent vertices, in the case of the tetrahedron). The 550 boundary yods correspond to the 550 SLs in CTOL. The 10 vertices lying on the axes of the five Platonic solids (their "poles") correspond to the 10 SLs that belong to the highest Tree in CTOL. The 540 hexagonal yods on the sides of the 180 tetractyses making up their 50 faces correspond to the 540 SLs in the 90 Trees below it. This is another way in which the five Platonic solids represent CTOL.
The number of yods in a Type B n-gon = 15n + 1 (see Section 2 in Power of the polygons/General view). 30n yods surround the centres of two separate, Type B n-gons. The first four separate, regular polygons of the inner Tree of Life are the triangle (n=3), square (n=4), pentagon (n=5) & hexagon (n=6). They have (3+4+5+6=18) corners. The number of yods surrounding the eight centres of the first (4+4) separate, Type B polygons = ∑30n = 30×18 = 540. They are the counterpart of the 540 hexagonal yods that line the 270 sides of the 180 tetractyses in the 50 faces of the five Platonic solids when these faces are Type A polygons. The holistic nature of the first (4+4) regular polygons is discussed in Article 48. This examplifies the Tetrad Principle discussed in Article 1 when it is applied to the regular polygons.
91 corners of triangles inside 5 Platonic solids
Suppose that the centre of
each Platonic solid is joined to its vertices. This creates E internal triangles, where E is the number of its
edges. When each triangle is Type A, the Platonic solid has 3E sectors of its internal triangles. They have (E+1)
corners. Noting that the five Platonic solids have 90 edges, the number of sectors of their internal
triangles = 3∑E = 3×90 = 270. The number of their corners = ∑(E+1) = 90 + 5 = 95. This
is the number value of Madim, the Mundane Chakra of Geburah. Next, suppose that the five
Platonic solids lie inside one another, sharing only a common centre. The number of internal corners = 91. This is
the number of Trees of Life in CTOL:
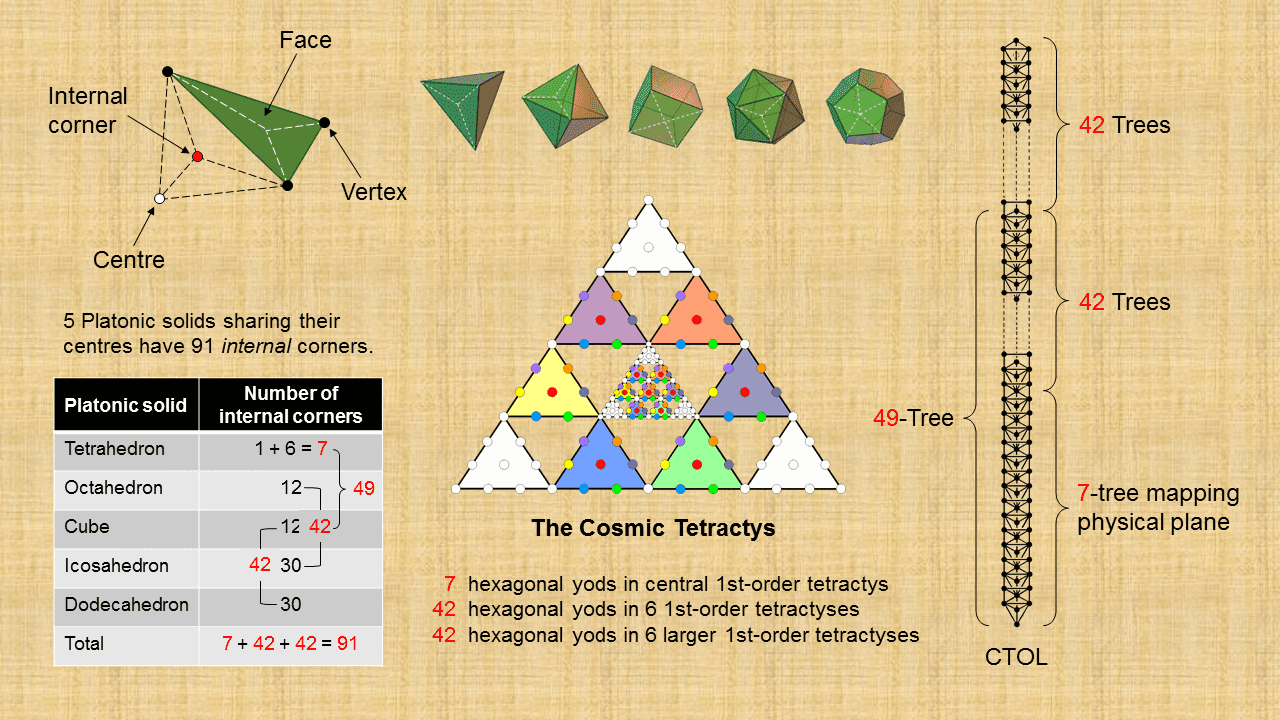
The interiors of the five Platonic solids sharing the same centre have 91 corners that correspond to the 91 Trees in CTOL. The tetrahedron has six edges that are sides of six internal Type A triangles. Their 18 sectors have seven corners. Inside the remaining four Platonic solids are 252 sectors with (91−7=84) corners. This 7:84 division in the 91 corners corresponds to the 7-tree mapping the physical plane and to the 84 Trees above it in CTOL. It also corresponds to the 84 coloured hexagonal yods in the Cosmic Tetractys that are outside the seven coloured hexagonal yods in its central tetractys. The octahedron and the icosahedron have 126 sectors of 42 internal Type A triangles with 42 corners other than their centres. Likewise, the cube and the dodecahedron have 42 corners in their interiors other than centres. One set of 42 corners corresponds to the 42 Trees of Life above the 7-tree in the 49-tree mapping the cosmic physical plane and to the 42 coloured hexagonal yods in the six smaller 1st-order tetractys in the Cosmic Tetractys; the other set of 42 corners corresponds to the 42 Trees above the 49-tree and to the 42 coloured hexagonal yods in the six larger 1st-order tetractyses in the Cosmic Tetractys. Remarkably, we see that the tetrahedron corresponds to the 7-tree mapping the physical plane, the octahedron & icosahedron correspond to the 42 Trees mapping the six superphysical planes and the cube & dodecahedron corresponds to the next 42 Trees mapping the six cosmic superphysical planes. There are three other possible combinations. However, the combination scheme just discussed seems the correct one, intuitively speaking, as the cube & dodecahedron have more external corners than the three other pairs of Platonic solids with 42 internal corners, a property that makes their correspondence with the cosmic superphysical planes more appropriate than these others pairs. The essential point that needs to be made here is the amazing fact that, constructed from Type A triangles, the five Platonic solids embody the same 7:42:42 pattern that exists for the physical plane with seven subplanes, the six superphysical planes with 42 subplanes and the six cosmic superphysical planes with 42 subplanes. This pattern must exist in the set of Platonic solids, the Cosmic Tetractys and CTOL because, being holistic systems, they must display analogous structural parameters.
| << Previous [1] 2 3 Next >> |