| << Previous 1 2 [3] Next >> |

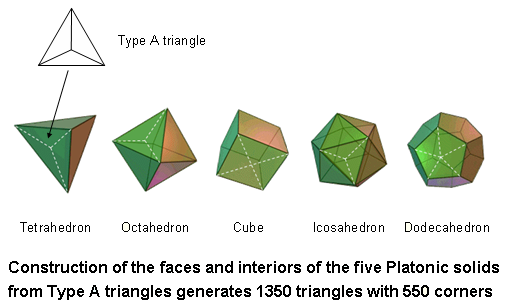
Suppose that the 50 faces of the five Platonic solids are divided into their 180 sectors. Then, suppose that their 50 vertices and the centres of their 50 faces with 90 edges are joined to their centres. This generates (90+180=270) internal triangles. When the (180+270=450) triangles in their faces and interiors are each divided into their three sectors, i.e., regarded as Type A triangles, the resulting (3×450=1350) simple triangles have (50+50+450=550) corners. (50+50+180=280) corners are in their faces and 270 corners are in their interiors. 280 is the number value of Sandalphon, the Archangel of Malkuth. ELOHIM, the Godname of Binah with number value 50, prescribes the five Platonic solids because they have 50 vertices, 50 faces and 500 (=50×10) corners of triangles that are not polyhedral vertices.
 |
|
|
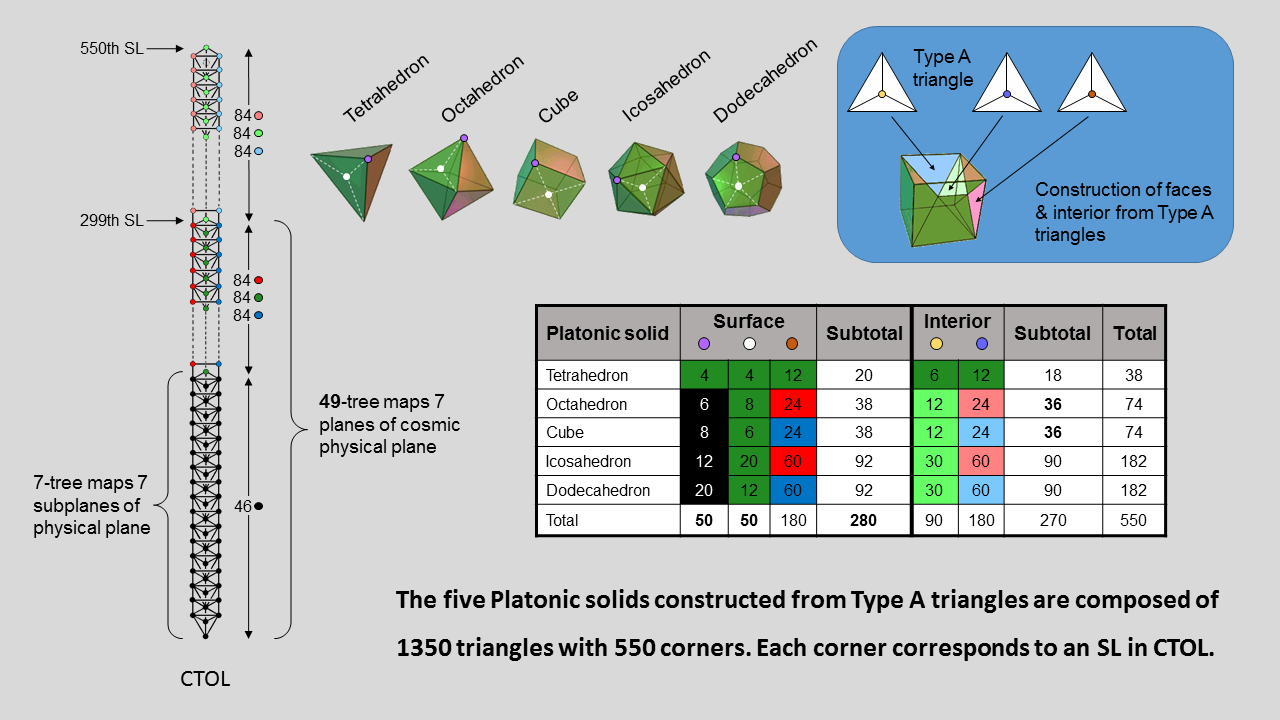
Suppose that the vertices of the five regular polyhedra are coloured violet, the centres of their faces are coloured white, the centres of the sectors of their faces are coloured brown, the centres of the internal triangles formed by their edges are coloured yellow and the centres of internal triangles formed by sides in the faces that are not edges are coloured purple. The table shows the numbers of corners of each colour. There are 280 corners in the faces and 270 inside the polyhedra, where 280 is the number value of Sandalphon, the Archangel of Malkuth. The former include (24+60=84) brown corners in the octahedron & icosahedron (dark red cells) and (24+60=84) brown corners in the cube & dodecahedron (dark blue cells). The latter includes (24+60=84) purple corners in the octahedron & icosahedron (light red cells) and (24+60=84) purple corners in the cube & dodecahedron (light blue cells). All four of these Platonic solids have (12+12+30+30=84) yellow corners, leaving (8+6+20+12=46) white corners, which, added to the 38 corners in the tetrahedron, creates a sixth set of 84 corners. We find that the 504 corners in the five Platonic solids other than the 46 vertices of the octahedron, cube, icosahedron & dodecahedron (the two pairs of regular polyhedra that are duals of each other) naturally group into six sets of 84.
Compare this with the distribution of SLs in CTOL:
The numbers tabulated in cells of a given colour add up to the number of SLs of the same colour. Notice that (84+84=168) light & dark green SLs line the central pillar from the top of the 7-tree to the top of CTOL. In other words, the number value 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth, specifies the very beginning in CTOL of the physical plane that is the space-time continuum! The 252 internal corners in the octahedron, cube, icosahedron & dodecahedron correspond to the 252 SLs that span the 42 Trees of Life mapping the six cosmic superphysical planes; the 252 corners in either their faces or in the tetrahedron correspond to the 252 SLs that span the 42 Trees mapping the six superphysical planes of the cosmic physical plane; the 46 remaining vertices correspond to the 46 SLs up to, but not including, the top of the 7-tree, which maps the physical plane. An analogous pattern is exhibited by the Sri Yantra (see here for details).
There are (280+18=298) corners in either the tetrahedron or the faces of the four other Platonic solids. This is the number of SLs up to (but excluding) the top of the 49-tree mapping the 49 subplanes of the cosmic physical plane.
The 550 points that surrounding the centres of the five Platonic solids when they are constructed from Type A triangles symbolize the 550 SLs of CTOL. More generally, their embodiment of this parameter of holistic systems demonstrates their holistic nature. The fact that they are composed of 1350 triangles is another indication of this because this number, too, is a holistic parameter, being the number of yods outside the root edge in the (7+7) enfolded Type B polygons containing 1370 yods that are not shared with the outer Tree of Life:
 |
 |
Their 50 faces have 180 triangular sectors with (90+180=270) sides. When the triangles are Type A, (3×180=540) sides are added, making a total of 810 sides. Joining the (50+50=100) vertices & face-centres to the centres of the five Platonic solids adds 100 sides, whilst the 270 internal triangles have (3×270=810) other sides when they are Type A. Hence, there are (810+100+810=1720) sides. The number of corners, sides & triangles in the five Platonic solids = 550 + 1720 + 1350 = 3620 = 362×10, where 362 is the number of yods in the two Type B dodecagons present in the inner form of the Tree of Life:
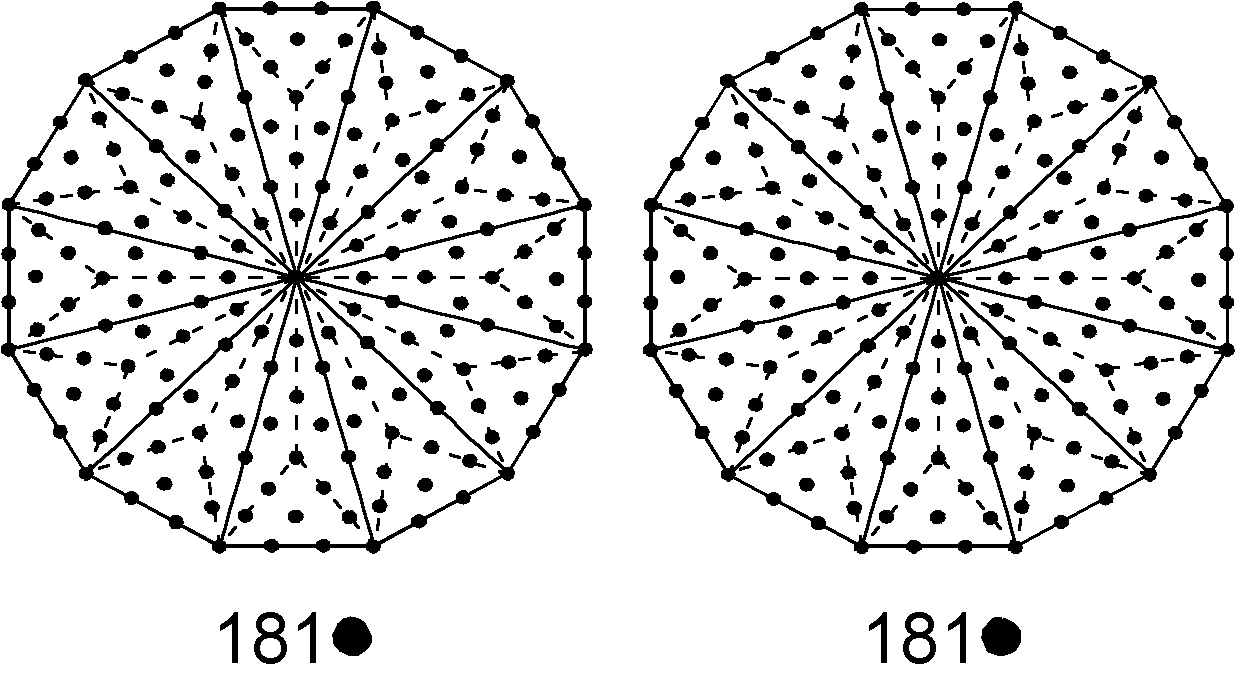
Each dodecagon embodies (apart from the Pythagorean factor of 10) the number of geometrical elements in each half of the five Platonic solids. Of these geometrical elements, 20 corners & sides make up their axes, which are therefore surrounded by (3620−20=3600) geometrical elements, 1800 being in the five upper halves and 1800 being in their five lower halves. As 1800 = 50×36, where 50 is the number of ELOHIM, the Godname of Binah, and 36 is the number of ELOHA, the Godname of Geburah, the Sephirah below Binah in the Tree of Life, we see how these Sephiroth on the Pillar of Judgement determine the geometrical composition of the regular polyhedral representation of the Tree of Life. On average, the number of geometrical elements surrounding the axis of a Platonic solid constructed from Type A triangles = 3600/5 = 720. There are 360 (=36×10) such geometrical elements on average in each half of a Platonic solid. They correspond to the 360 yods surrounding the centres of the two Type B dodecagons. The number 720 = 72×10, where 72 is the number of Chesed, the Sephirah opposite Geburah in the outer Tree of Life. The centre of a decagon whose sectors are 2nd-order tetractyses is surrounded by 720 yods,* whilst the centres of the seven separate polygons of the inner Tree of Life are surrounded by 720 yods when all the polygons are Type B.**

Their possession of this parameter of the inner Tree of Life demonstrates the holistic character of the five Platonic solids — how they embody archetypal numbers that parameterise any holistic system. The number 720 appears also in the first four Platonic solids, as well as in the disdyakis triacontahedron (see Fig. 7 here) and as the 720 edges of the 600-cell, which is the polychoron counterpart of each half of the inner form of 10 Trees of Life (see section entitled "The holistic 120:720 division in the two 600-cells and in sacred geometries" here).
| << Previous 1 2 [3] Next >> |