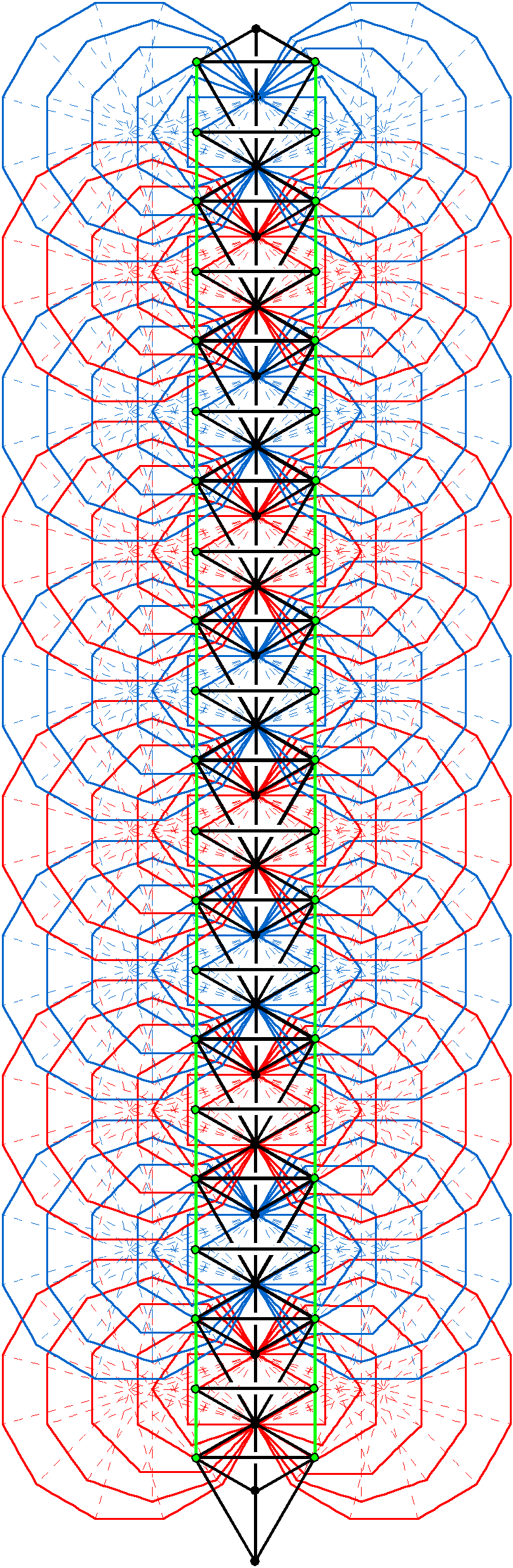

C.W. Leadbeater (1854-1934) said that he checked 135 times his count of the number (1680) of circular turns in a helical whorl of the UPA. It is therefore unreasonable to doubt the accuracy of this number.
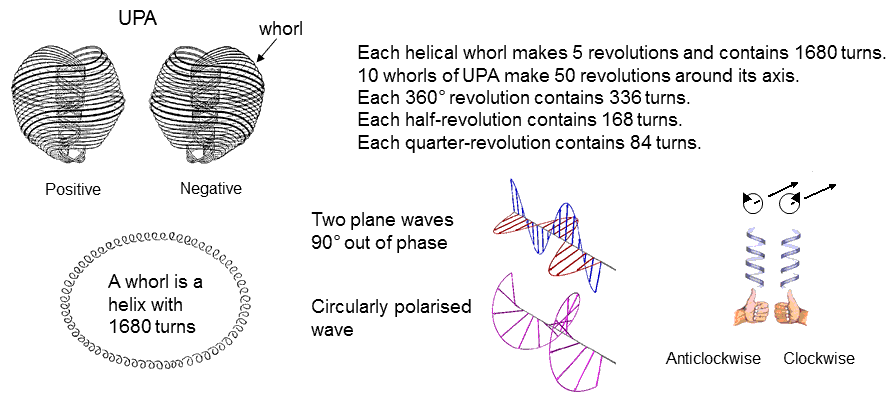
The positive and negative UPAs have, respectively, 16800 clockwise and anticlockwise, circularly polarised waves in their 10 whorls.
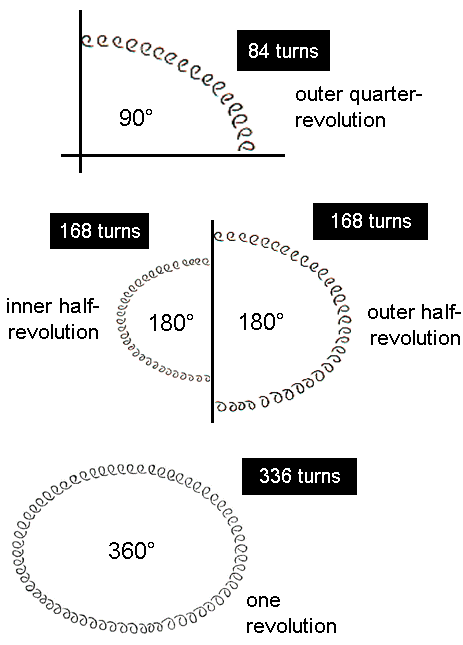
Each half-revolution of a whorl comprises 168 circular turns. There are 336 turns in an outer & an inner half of a whorl. The 10 whorls of the UPA comprise 1680 turns in a half-revolution of its outer half and 1680 turns in a inner half-revolution. Each whorl revolves 5 times around the axis of spin (2½ times in an outer spiral from the top of the UPA to its nadir and 2½ times in an inner spiral that returns to the top).
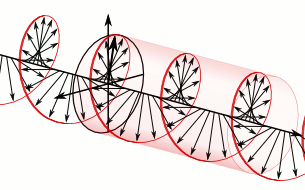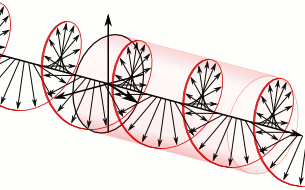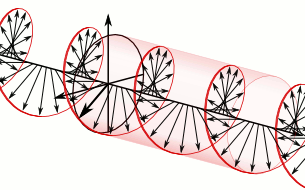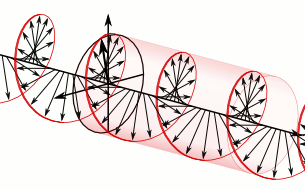
Anticlockwise rotation
Superposition of two plane waves 90° out of phase generates a circularly polarised wave whose constant amplitude rotates in a circle whose plane is perpendicular to the direction of motion of the two waves. This can be either anticlockwise or clockwise, depending upon whether the oscillation in the XZ plane, respectively, lags 90° behind or is 90° ahead of the wave in the XY plane.
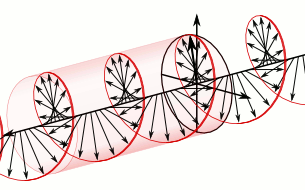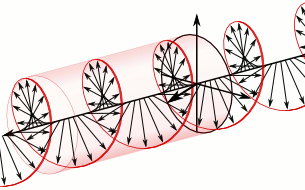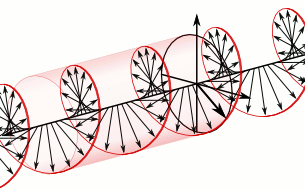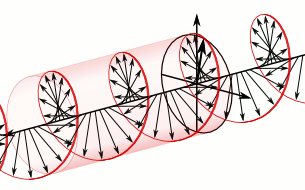
Mirror image of anticlockwise rotation
If the direction of the constant amplitude of oscillation rotates anticlockwise when viewed in the direction that the circularly polarised wave travels, the mirror image of this wave is one that travels with its constant amplitude rotating in the clockwise sense when viewed in the direction of its travel.
→
Identical to
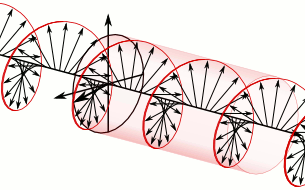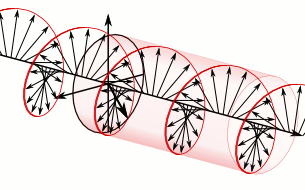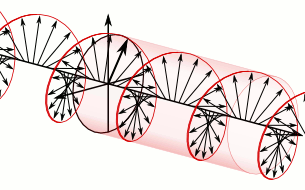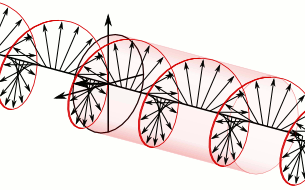
Clockwise rotation
The mirror image of an anticlockwise polarised wave is one that has a clockwise rotation.
10 sets of 168 intrinsic geometrical elements outside the root edge of the 7 enfolded polygons → inner half-revolution of the 10 helical whorls of the UPA, each having 168 turns. Each bit of information generating the geometry of the inner Tree of Life manifests in the E8×E8 heterotic superstring as an oscillation of a circularly polarised wave travelling along each whorl.
10 sets of 168 intrinsic geometrical
elements outside the root edge of the 7 enfolded polygons → outer half-revolution of the 10
helical whorls of the UPA, each having 168 turns. Each bit of
information generating the geometry of the inner Tree of Life manifests in the
E8×E8 heterotic superstring as an oscillation of a circularly polarised
wave travelling along each whorl.
The 7 enfolded, Type A polygons making up each half of the inner form
of the Tree of Life have 168 corners. sides & triangles outside their root
edge that are unshared with the triangles belonging to the outer Tree of Life. Outside the root
edge of the (7+7) enfolded polygons that make up the complete inner form of the Tree of Life are
(168+168=336) intrinsic geometrical elements. The inner form of
10 Trees of Life has (70+70=140) enfolded polygons with (1680+1680=3360) intrinsic
geometrical elements outside their root edges. Each Tree represents a whorl of the UPA because its
10 whorls are the Sephirothic manifestation in the subatomic world of the Tree of Life
blueprint. Because the helical whorls wind 5 times around the the axis of the UPA, each revolution
of a whorl has 336 turns. A complete revolution of all 10 whorls comprises (10×336=3360) turns,
their 5 revolutions totalling 16800 turns. Every geometrical element intrinsic to the inner form of
10 Trees of Life, each mapping a whorl of the UPA, corresponds to a circular turn
(Leadbeater's "1st-order spirilla") as one complete cycle of oscillation of a circularly polarised
wave (360° rotation of its constant amplitude).
As pointed out in (2) in #42, the decagon & dodecagon have 84 unshared corners, sides & triangles, as do the triangle, square, pentagon, hexagon & octagon. This 84:84 division of the holistic parameter 168 displayed by the first 5 polygons and the last two polygons is characteristic of holistic systems (see Article 64 and the examples discussed at the end of #45). In the E8×E8 heterotic superstring, it manifests as the 84 pairs of perpendicular, sinusoidal waves oscillating 90° out of phase whose superposition creates 84 circular turns spread along each quarter-revolution of a whorl of the UPA, this being the ground state of the subquark state of this superstring. In the 7 diatonic musical scales, it exists as the 84 rising intervals that are repetitions of the 6 notes between the tonic and octave of the Pythagorean scale and as their 84 falling interval counterparts (see #43 in The seven musical scales).