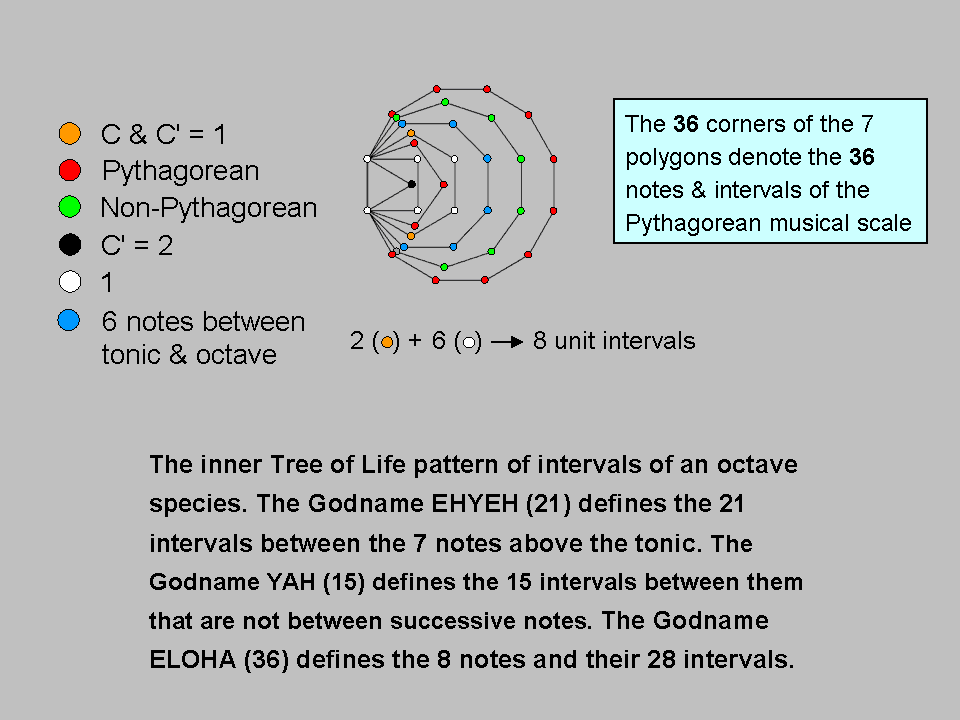
There are 28 intervals between the eight notes spanning an octave. Including the unit interval between a note and itself, there are 36 intervals. ELOHA, the Godname of Geburah with number value 36, (see here) prescribes the basic number of intervals between the notes. This is true not only for the Pythagorean scale but for any eight-note scale. The 36 intervals constitute a Tree of Life pattern because the seven enfolded polygons of the inner form of the Tree of Life have 36 corners. YAH, the Godname of Chokmah with number value 15, prescribes the 15 intervals between the seven notes above the tonic that are not between successive notes. EHYEH, the Godname of Kether with number value 21, prescribes the 21 intervals between these seven notes. Alternatively, the six notes between the tonic & octave have 15 intervals, leaving 21 intervals consisting of the eight unit intervals, the octave, the six intervals between these six notes and the tonic and the six intervals between them and the octave.

It might be thought that the eight corners of the octagon correspond to the eight unit intervals. However, this is incorrect because one of these intervals is that between the octave and itself and, as this note is the first note of the next higher octave C′, this interval is shared between the two octaves, which means that it has to be assigned to the topmost corner of the hexagon, which coincides with the lowest corner of the hexagon enfolded in the next higher, overlapping Tree of Life (this is the only polygonal corner that is shared between polygons enfolded in successive Trees of Life). The orange yods of the lowest and highest corners of the hexagon, therefore, denote, respectively, the unit interval between the tonic and itself and the unit interval between the octave and itself. The distribution of the other notes & intervals is less clear. However, noting that there are 13 Pythagorean intervals other than notes and eight non-Pythagorean intervals, and making the intuitive assumption that the two endpoints of the root edge denote either unit intervals or two of the primary notes F, G & C′ and that Pythagorean and non-Pythagorean intervals are not symbolized by corners of the same polygon, then the former must be assigned to the three external red corners of the pentagon and the ten red external corners of the dodecagon, whilst the latter must be assigned to the eight external green corners of the decagon. The six notes between the tonic & octave must be assigned to the six external blue corners of the octagon and the six remaining unit intervals must be assigned to the white corners of the square & the two remaining white corners of the hexagon, with the octave assigned to the black corner of the triangle. Alternatively, these six notes could be assigned to the six white corners, although this possibility seems less plausible because they would then be spread over more than one polygon.

 

<< Previous    1...   12  13  [14]  15  16  ...45    Next >>

Home